[Java·算法·困难]LeetCode32. 最长有效括号
每天一题,防止痴呆
- 题目
- 示例
- 分析思路1
- 题解1
- 分析思路2
- 题解2
- 分析思路3
- 题解3
👉️ 力扣原文
题目
给你一个只包含 '(' 和 ')' 的字符串,找出最长有效(格式正确且连续)括号子串的长度。
示例
输入:s = "(()"
输出:2
解释:最长有效括号子串是 "()"
输入:s = ")()())"
输出:4
解释:最长有效括号子串是 "()()"
输入:s = ""
输出:0
输入:s = "(())("
输出:4
分析思路1
用栈的解法:
- 定义一个栈,用于存储字符在字符串中的下标。初始化时,将-1压入栈中。
- 从字符串的左边开始遍历,如果遇到左括号,则将其下标压入栈中。
- 如果遇到右括号,则弹出栈顶元素,表示与该右括号匹配的左括号已经找到。如果此时栈为空,则将该右括号的下标压入栈中,表示该右括号没有匹配的左括号。
- 如果栈不为空,则计算当前子串的长度,即当前右括号的下标减去栈顶元素的值。如果该子串的长度大于最长子串的长度,则更新最长子串的长度。
题解1
class Solution {public int longestValidParentheses(String s) {int maxLen = 0;Stack<Integer> stack = new Stack<>();stack.push(-1);//有效括号长度为当前右括号下标减去栈底元素,初始化要是-1才对for (int i=0; i<s.length(); i++){char c = s.charAt(i);if(c == '('){stack.push(i);}else {stack.pop();//弹出栈顶if(stack.isEmpty()){ // 栈为空,说明当前右括号没有与之匹配的左括号stack.push(i);// 将当前右括号下标压入栈中}else {// 栈不为空,计算有效括号长度int len = i - stack.peek();maxLen = Math.max(maxLen, len);}}}return maxLen;}}
执行结果
分析思路2
双指针:
在此方法中,我们利用两个计数器 left 和 right 。首先,我们从左到右遍历字符串,对于遇到的每个 ‘(’,我们增加 left 计数器,对于遇到的每个 ‘)’ ,我们增加 right 计数器。每当 left 计数器与 right 计数器相等时,我们计算当前有效字符串的长度,并且记录目前为止找到的最长子字符串。当 right 计数器比 left 计数器大时,我们将 left 和 right 计数器同时变回 0。
这样的做法贪心地考虑了以当前字符下标结尾的有效括号长度,每次当右括号数量多于左括号数量的时候之前的字符我们都扔掉不再考虑,重新从下一个字符开始计算,但这样会漏掉一种情况,就是遍历的时候左括号的数量始终大于右括号的数量,即 (() ,这种时候最长有效括号是求不出来的。
解决的方法也很简单,我们只需要从右往左遍历用类似的方法计算即可,只是这个时候判断条件反了过来:
当left 计数器比right 计数器大时,我们将left 和 right 计数器同时变回 0
当 left 计数器与 right 计数器相等时,我们计算当前有效字符串的长度,并且记录目前为止找到的最长子字符串
这样我们就能涵盖所有情况从而求解出答案。
题解2
class Solution {public int longestValidParentheses(String s) {int left=0,right=0,maxLen=0;for (int i = 0; i < s.length(); i++) {if(s.charAt(i)=='('){left++;}else {right++;}if(left == right){maxLen = Math.max(maxLen, right*2);}else if(right > left){left = right = 0;}}left = right = 0;for (int i = s.length()-1; i >= 0 ; i--) {if(s.charAt(i)=='('){left++;}else {right++;}if(left == right){maxLen = Math.max(maxLen, right*2);}else if(left > right){left = right = 0;}}return maxLen;}}
执行结果
分析思路3
使用动态规划:
我们定义一个一维数组 dp,其中 dp[i] 表示以 i 位置结尾的有效括号子串的最长长度。在计算 dp[i] 时,我们需要根据 s[i] 的值进行分类讨论:
1.当 s[i] 为左括号 ‘(’ 时,以 i 位置结尾的子串肯定不是有效括号子串,因此 dp[i] = 0。
2.当 s[i] 为右括号 ‘)’ 时,我们需要找到与其匹配的左括号。具体来说,我们可以先计算前面已经形成的有效括号长度 preLen,然后在 i - preLen - 1 的位置寻找与当前的右括号相匹配的左括号,即 s[pre]。如果 s[pre] 为左括号,则当前的右括号可以与其闭合,有效长度增加2。此时,我们还需要再往前看一眼,是否还有有效长度,如果有,合并过来。例如:“()(()())” 当前在计算最后一个位置时,dp[7] 已经等于 dp[6]+2 = 4+2,但需要再往前看一眼,dp[1] 还有有效长度,合并过来 dp[7] = 4+2+2。那是否还需要再往前看?不需要了,因为,如果前面还有有效长度,其长度肯定已经合并到 dp[2] 上了。因此,每次只需要再往前多看一眼就可以。
最终答案是 dp 数组中的最大值。
题解3
class Solution {// 子串问题:严格以每个结尾计算个答案,最终答案必在其中public static int longestValidParentheses(String s) {if (s == null || s.length() < 2) return 0;int[] dp = new int[s.length()]; // dp[i]:严格以i位置结尾,形成的有效括号子串最长长度是多少int max = 0; // 最终的答案// dp[0] = 0; // 默认for (int i = 1; i < s.length(); i++) {// if (s.charAt(i) == '(') dp[i] = 0; 以左括号结尾,无效if (s.charAt(i) == ')') {int preLen = dp[i - 1]; // 前面已经形成的有效括号长度int pre = i - 1 - preLen; // 寻找与当前的右括号相匹配的左括号位置:前面有效括号长度再往前一个位置if (pre >= 0 && s.charAt(pre) == '(') { // 如果寻找到左括号:前面有效括号长度再往前一个位置是左括号dp[i] = dp[i-1] + 2; // 可以与当前的右括号闭合,有效长度增加2// 【注意】此时,需要再往前看下,是否还有有效长度,如果有,合并过来// 例如:"()(()())" 当前在计算最后一个位置时,dp[7]已经等于 dp[6]+2 = 4+2// 但需要再往前看一眼,dp[1]还有有效长度,合并过来 dp[7] = 4+2+2// 那是否还需要再往前看?// 不需要了,因为,如果前面还有有效长度,其长度肯定已经合并到dp[2]上了// 因此,每次只需要再往前多看一眼就可以if (pre-1 >= 0) {dp[i] += dp[pre-1];}}max = Math.max(max, dp[i]); // 严格以每个结尾抓一个答案,最终答案必在其中}}return max;}}
执行结果
相关文章:

[Java·算法·困难]LeetCode32. 最长有效括号
每天一题,防止痴呆题目示例分析思路1题解1分析思路2题解2分析思路3题解3👉️ 力扣原文 题目 给你一个只包含 ( 和 ) 的字符串,找出最长有效(格式正确且连续)括号子串的长度。 示例 输入:s "(()&q…...

pytorch如何搭建一个最简单的模型,
一、搭建模型的步骤 在 PyTorch 中,可以使用 torch.nn 模块来搭建深度学习模型。具体步骤如下: 定义一个继承自 torch.nn.Module 的类,这个类将作为我们自己定义的模型。 在类的构造函数 __init__() 中定义网络的各个层和参数。可以使用 to…...

JS实现css的hover效果,兼容移动端
Hi I’m Shendi JS实现css的hover效果,兼容移动端 功能概述 CSS的hover即触碰时触发,在电脑端鼠标触碰,移动端手指触摸 有的时候光靠css实现不了一些效果,例如元素触发hover,其他元素触发动画效果,所以需要…...
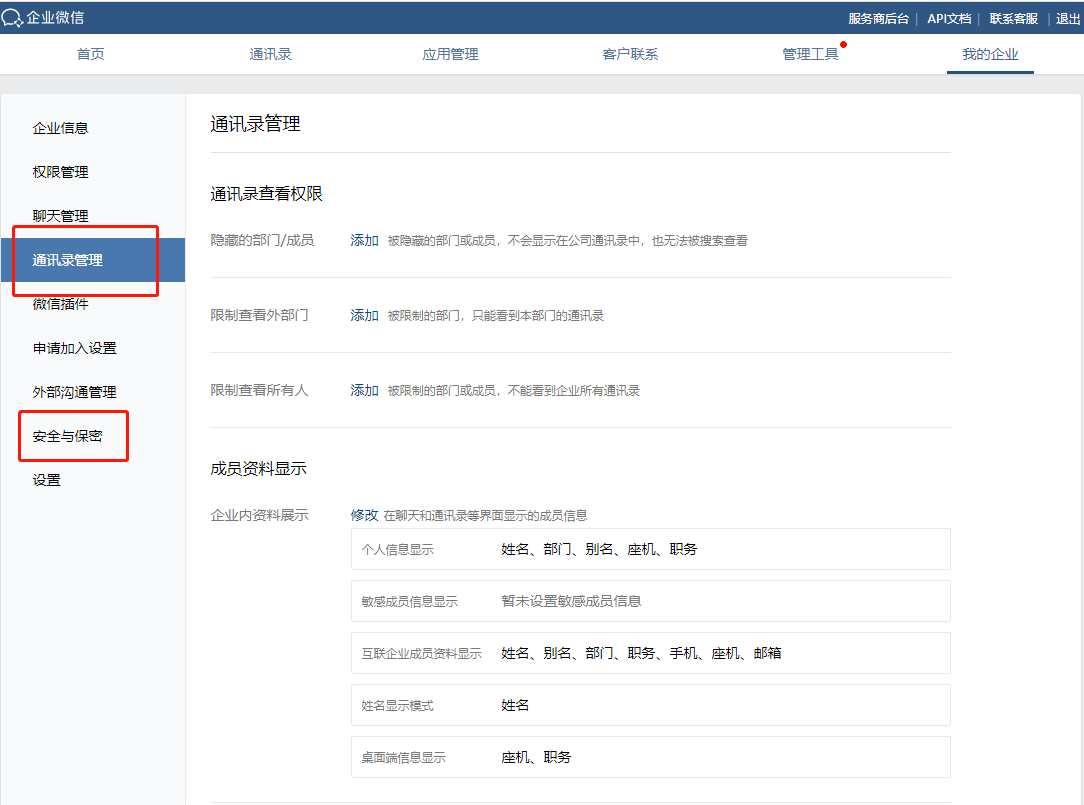
企业微信的后台怎么进入和管理?
企业微信管理后台,只有企业的管理员才可以进企业微信后台,普通员工想要进入后台、可以联系管理员将你设置为后台管理员。 一、怎么进入企业微信后台 管理员进入企业微信后台有两种路径; 路径一: 企业管理员直接在浏览器搜索企…...

【2223sW2】LOG2
写在前面 好好学习,走出宿舍,走向毕设! 一些心路历程记录,很少有代码出现 因为鬼知道哪条代码到时候变成毕设的一部分了咧,还是不要给自己的查重挖坑罢了 23.3.2 检验FFT 早上师兄帮忙看了一眼我画的丑图ÿ…...
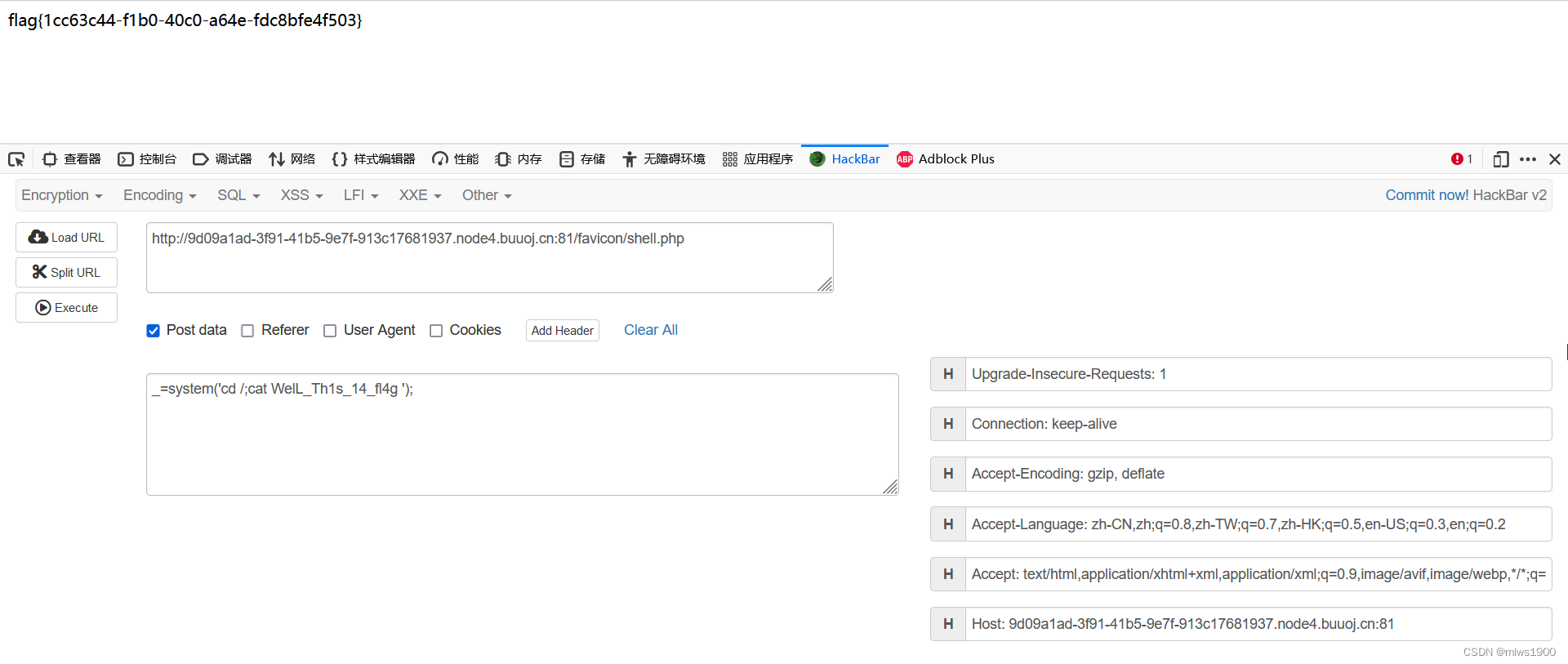
buuctf-web-[SUCTF 2018]MultiSQL1
打开界面,全部点击一遍,只有注册和登录功能可以使用注册一个账号,注册admin提示用户存在,可能有二次注入,注册admin自动加了一个字符,无法二次注入,点击其他功能点换浏览器重新登录后࿰…...
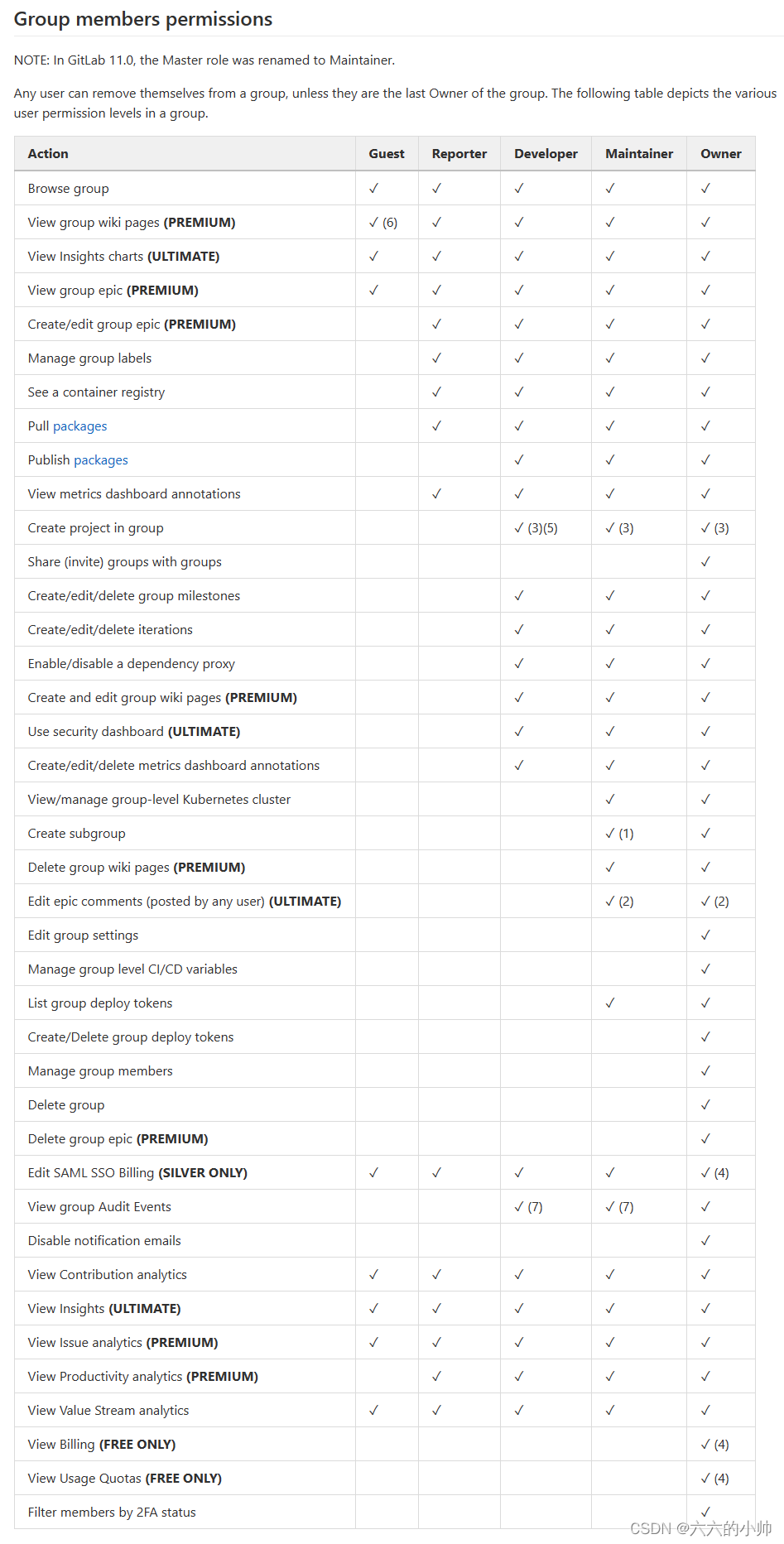
GitLab创建仓库分配权限
文章目录创建仓库分配权限参考资料创建仓库 点击“New project”创建新项目 分配权限 点击左侧菜单栏“Members”成员,菜单 “Invite member”邀请成员,添加人员;“Invite group”邀请组织,添加一个组织所有成员下面输入框搜索…...
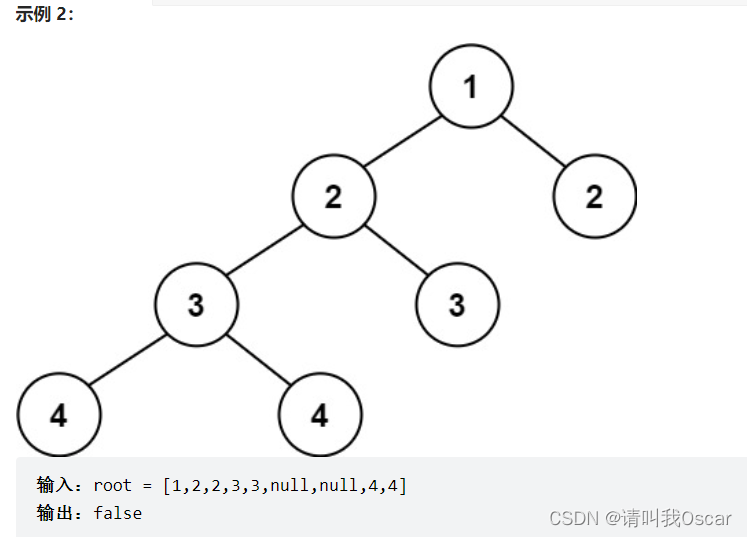
代码随想录-51-110.平衡二叉树
目录前言题目1.求高度和深度的区别节点的高度节点的深度2. 本题思路分析:3. 算法实现4. pop函数的算法复杂度5. 算法坑点前言 在本科毕设结束后,我开始刷卡哥的“代码随想录”,每天一节。自己的总结笔记均会放在“算法刷题-代码随想录”该专…...

项目实战典型案例27——对生产环境以及生产数据的敬畏之心
对生产环境以及生产数据的敬畏之心一:背景介绍总结升华一:背景介绍 本篇博客是对项目开发中出现的对生产环境以及生产数据的敬畏之心行的总结并进行的改进。目的是将经历转变为自己的经验。通过博客的方式分享给大家,大家一起共同进步和提高…...
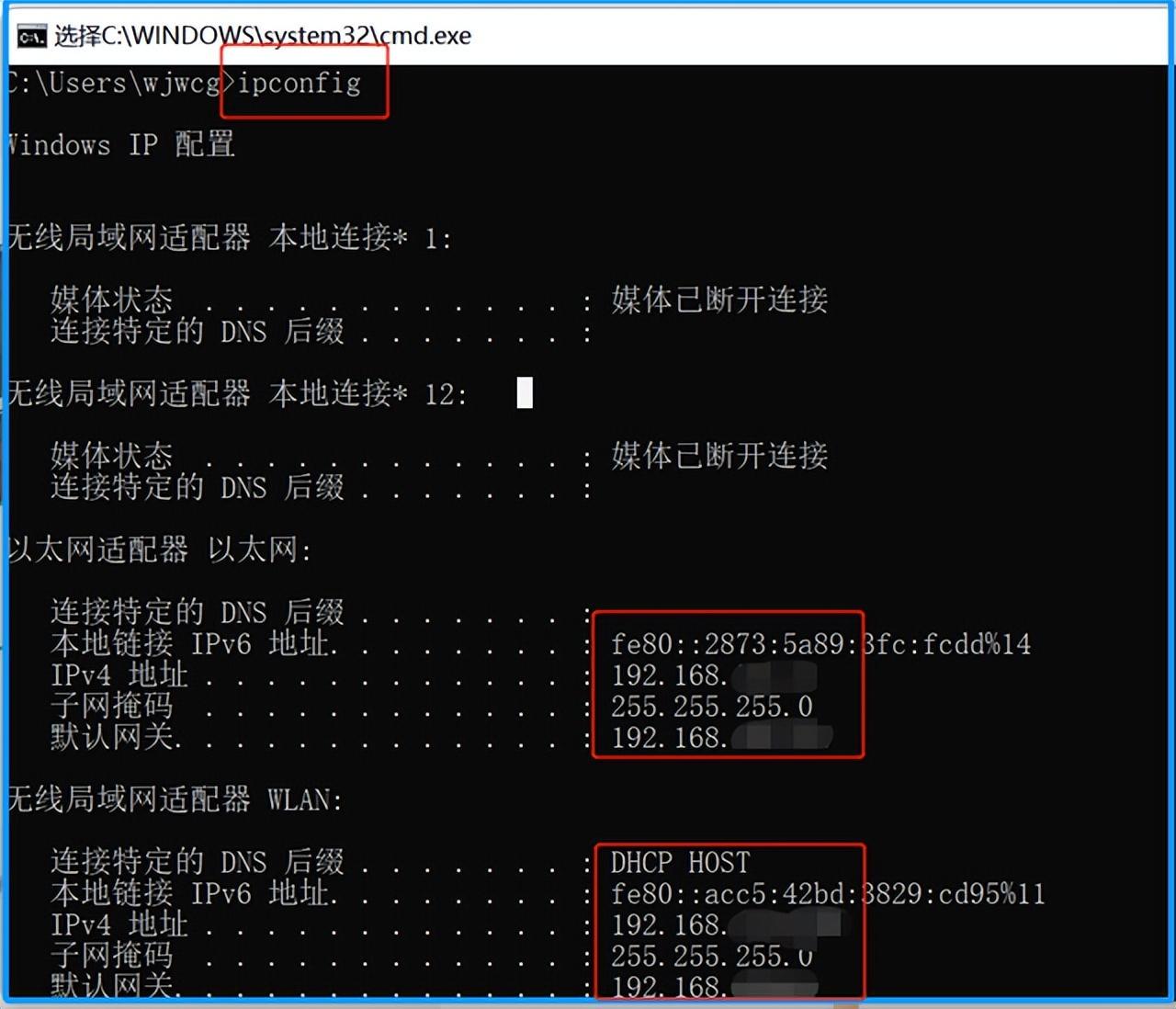
如何查找你的IP地址?通过IP地址能直接定位到你家!
我们ip地址分为A、B、C、D、E共5类,每一类地址范围不同,从A到Eip地址范围依次递减,其中哦,D和E是保留地址,我们用不了。A、B、C3类地址很多都被美国这样的西方国家分走了,而留给我们的就剩有限的地址了&…...

Containers--array类
Array 类 简介 Array 类是一个固定大小的数组,它的大小在编译时就已经确定了。Array 类的大小是固定的,因此它的大小不能改变。 数组是固定大小的序列容器:它们以严格的线性顺序保存特定数量的元素。 在内部,数组除了包含的元素之外不保留…...
LinqConnect兼容性并支持Visual Studio 2022版本
LinqConnect兼容性并支持Visual Studio 2022版本 现在支持Microsoft Visual Studio 2022版本17.5预览版。 添加了Microsoft.NET 7兼容性。 共享代码-共享相同的代码,以便在不同的平台上处理数据。LinqConnect是一种数据库连接解决方案,适用于不同的基于.…...
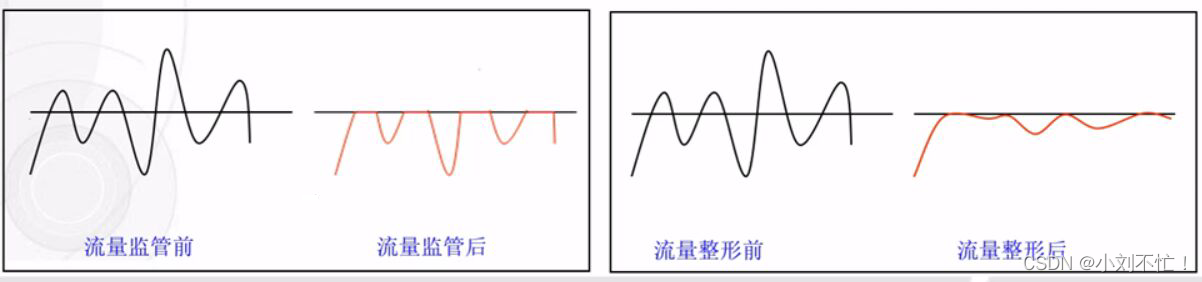
流量监管与整形
流量监管与整形概览流量监管介绍流量监管令牌桶流量监管的具体实现单桶单速流量监管双桶单速流量监管双桶双速流量监管流量整形介绍GTS(Generic Traffic Shaping)LR(Line Rate)流量整形与流量监管的区别概览 流量整形是对报文的速…...

详解init 容器
什么是init容器 init 容器是一种特殊容器,在 Pod 内的应用容器启动之前运行。Init 容器可以包括一些应用镜像中不存在的实用工具和安装脚本。 你可以在 Pod 的规约中与用来描述应用容器的 containers 数组平行的位置指定 Init 容器 每个 Pod 中可以包含多个容器&…...

RequestResponseBodyMethodProcessor
既是一个参数解析器,也是一个返回结果处理器。 1.持有消息转换器的集合 protected final List<HttpMessageConverter<?>> messageConverters;2.作为参数解析器,例如对RequestBody标识的参数进行解析 判断是否支持当前类型的参数 Overrid…...
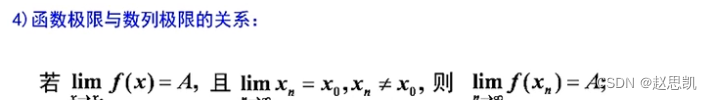
函数的极限
目录 函数的极限 函数极限的定义: 例题: 左右极限: 自变量趋于无穷大时函数的极限: 例题: 函数极限的性质: 函数极限与数列极限之间的关系: 函数的极限 函数极限的定义: 一句…...

dnf命令使用
1. 简介 DNF是新一代的rpm软件包管理器。他首先出现在 Fedora 18 这个发行版中。而最近,它取代了yum,正式成为 Fedora 22 的包管理器 DNF包管理器克服了YUM包管理器的一些瓶颈,提升了包括用户体验,内存占用,依赖分析…...
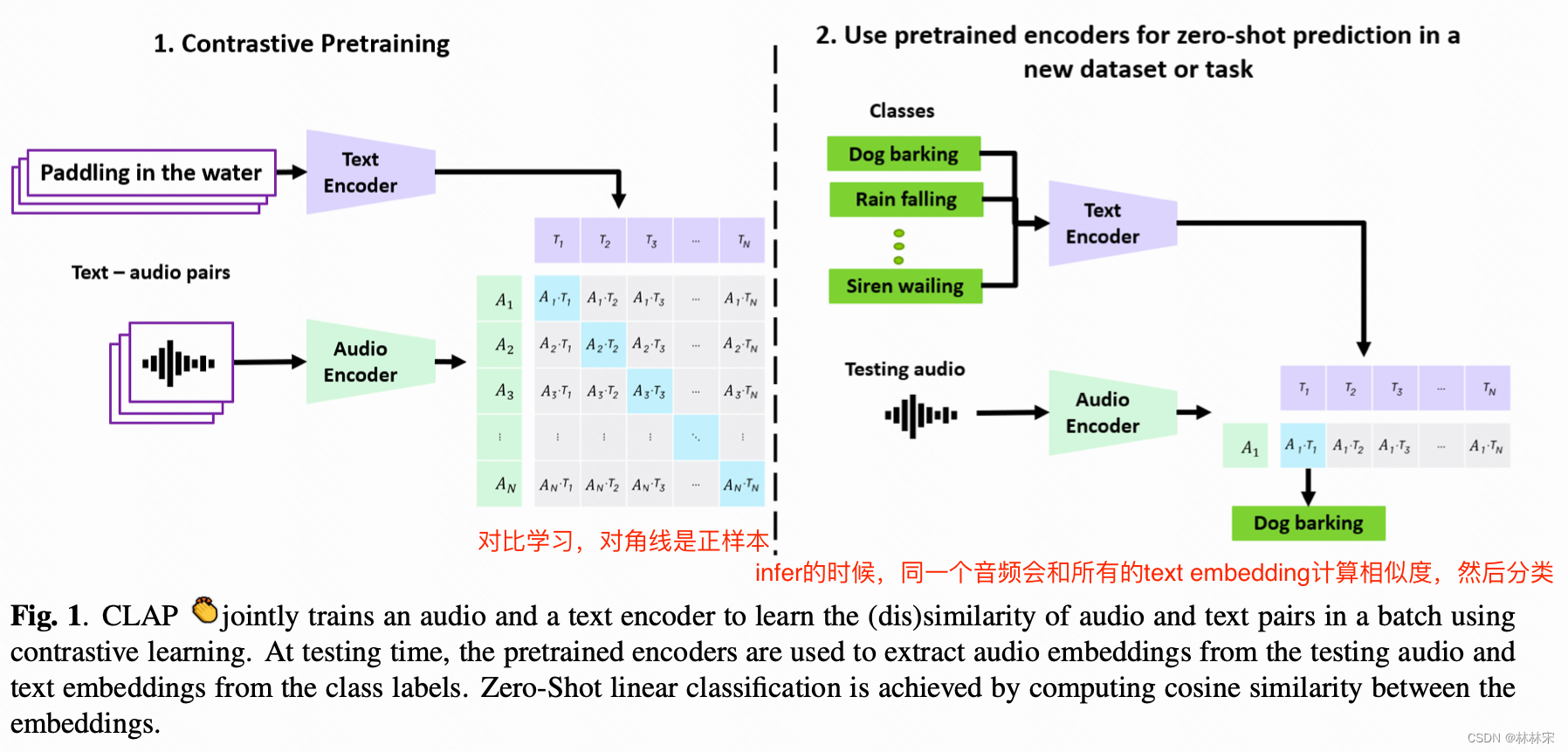
CLIP CLAP
文章目录CLIPabstractintroCLAP: LEARNING AUDIO CONCEPTS FROM NATURAL LANGUAGE SUPERVISIONabstractmethodCLIP open AI2021.2代码&预训练模型 abstract 原有的基于有监督数据训练的计算机分类任务,在面对新的分类目标时泛化性和可用性都会变差࿱…...

Debezium报错处理系列之五十二:解决Sql Server数据库安装后修改主机名导致sqlserver数据库实例名称没有修改从而无法设置CDC的问题
Debezium报错处理系列之五十二:解决Sql Server数据库安装后修改主机名导致sqlserver数据库实例名称没有修改从而无法设置CDC的问题 一、完整报错二、错误原因三、解决方法Debezium报错处理系列一:The db history topic is missing. Debezium报错处理系列二:Make sure that t…...

scratch老鹰捉小鸡 电子学会图形化编程scratch等级考试二级真题和答案解析2022年12月
目录 scratch老鹰捉小鸡 一、题目要求 1、准备工作 2、功能实现 二、案例分析 <...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...
