【算法】Cordic算法的原理及matlab/verilog应用
一、前言
单片机或者FPGA等计算能力弱的嵌入式设备进行加减运算还是容易实现,但是想要计算三角函数(sin、cos、tan),甚至双曲线、指数、对数这样复杂的函数,那就需要费些力了。通常这些函数的计算需要通者查找表或近似计算(如泰勒级数逼近)等技术来转换为硬件易于实现的方式。
CORDIC(Coordinate Rotation Digital Computer, 坐标旋转数字计算方法)算法就是一种化繁为简的算法,通过基本的加减和移位运算代替乘法运算,逐渐逼近目标值,得出函数的数值解。
二、Cordic算法理论推导
理论推导参考:CORDIC算法理论详解_cordic算法详解-CSDN博客,这篇博客的推导仔细而全面。
Cordic算法的基石在于一个规律:从tan45°开始,角度每减半,tan值也接近减半。这一规律直接将三角函数运算变成2的幂运算,而这在数字电路中可直接用移位运算来实现。
三、Cordic算法 matlab实现
3.1 已知相位(角度)求坐标(正弦余弦)
function [sin_theta,cos_theta] = cordic_sincos(theta,n)
% n:iterations
% theta: -180~180
tan_table = 2.^-(0 : n-1);
angle_rad_lut = atan(tan_table);
%angle_deg_lut = rad2deg( atan(tan_table) );k = 1;
for i = 0 : n-1k = k*(1/sqrt(1 + 2^(-2*i)));
endx = k;
y = 0;
theta_tar = theta*pi/180; % to be rad
z=theta_tar;% preprocess
if (theta_tar > pi/2) theta_tar = theta_tar - pi/2;
elseif (theta_tar < -pi/2)theta_tar = theta_tar + pi/2;
endfor i = 0 : n-1 if (z > 0) d =1;elsed=-1;endx_temp = x;y_temp =y;z_temp = z;x= x_temp - d*y_temp*2^(-i);y = y_temp + d*x_temp*2^(-i);z = z_temp - d*angle_rad_lut(i+1);endif (theta_tar > pi/2) sin_theta = -x;cos_theta = y;
elseif (theta_tar < -pi/2)sin_theta = x;cos_theta = -y;
elsesin_theta = y;cos_theta = x;
end
end3.2 已知坐标求相位
待实现
四、cordic算法的verilog实现
待实现
相关文章:

【算法】Cordic算法的原理及matlab/verilog应用
一、前言 单片机或者FPGA等计算能力弱的嵌入式设备进行加减运算还是容易实现,但是想要计算三角函数(sin、cos、tan),甚至双曲线、指数、对数这样复杂的函数,那就需要费些力了。通常这些函数的计算需要通者查找表或近似…...
QT:信号与槽
作业: 完善对话框,点击登录对话框,如果账号和密码匹配,则弹出信息对话框,给出提示”登录成功“,提供一个Ok按钮,用户点击Ok后,关闭登录界面,跳转到其他界面 如果账号和…...
以动态库链接库 .dll 探索结构体参数
Dev c C语言实现第一个 dll 动态链接库 创建与调用-CSDN博客 在写dll 插件中发现的函数指针用途和 typedef 的定义指针的用法-CSDN博客 两步之后,尝试加入结构体实现整体数据使用。 注意结构体 Ak 是相同的 代码如下 DLL文件有两个,dll.dll是上面提到…...
vue快速入门(三)差值表达式
注释很详细,直接上代码 上一篇 新增内容 插值表达式基本用法插值表达式常用公式 源码 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-wid…...
RabbitMQ的交换机与队列
一、流程 首先先介绍一个简单的一个消息推送到接收的流程,提供一个简单的图 黄色的圈圈就是我们的消息推送服务,将消息推送到 中间方框里面也就是 rabbitMq的服务器,然后经过服务器里面的交换机、队列等各种关系(后面会详细讲&am…...

Spring的 IOC和AOP编程思想
Spring的IOC(控制反转)编程思想 IOC(Inversion of Control,控制反转)是Spring框架的核心思想之一。在传统的编程方式中,我们直接通过new关键字来创建对象,并直接调用对象的方法。这种方式下&am…...

Qt中显示hex数据的控件
效果类似QTextEdit,但是显示十六进制的数据,比如用于显示抓取串口或者bin文件的数据等等 chunks.h #ifndef CHUNKS_H #define CHUNKS_H/** \cond docNever *//*! The Chunks class is the storage backend for QHexEdit.** When QHexEdit loads data, C…...

python web 开发 - 常用Web框架
python web 开发 - 文章目录 python web 开发 -1、关于Web开发2、常用Web框架3、开发案例3.1. 使用Flask框架创建一个简单的Web应用程序3.2. 使用tornado框架创建一个简单的Web应用程序3.3. 使用Django框架创建一个简单的待办事项应用程序 4、总结 1、关于Web开发 Web当然是网…...

设计模式——适配器模式06
适配器模式 通常在已有程序中使用,至少有两个类的接口不兼容时,让相互不兼容的类能很好地合作。例如之前系统 用的Target 接口调用,现在要新增第三方接口Adaptee。如何进行适配,面向客户端提供 调用Target接口方式达到使用Adaptee…...
【鸿蒙开发】组件状态管理@Prop,@Link,@Provide,@Consume,@Observed,@ObjectLink
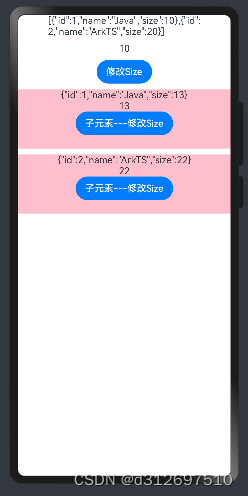
1. Prop 父子单向同步 概述 Prop装饰的变量和父组件建立单向的同步关系: Prop变量允许在本地修改,但修改后的变化不会同步回父组件。当父组件中的数据源更改时,与之相关的Prop装饰的变量都会自动更新。如果子组件已经在本地修改了Prop装饰…...

Web 前端性能优化之八:前端性能检测实践
五、前端性能检测实践 1、常用的检测工具 Lighthouse、Chrome开发者工具中与性能检测相关的一些工具面板、页面加载性能分析工具PageSpeed Insights、专业的性能检测工具WEBPAGETEST等 1、Chrome 任务管理器 通过Chrome任务管理器我们可以查看当前Chrome浏览器中࿰…...
安装VMware ESXi虚拟机系统
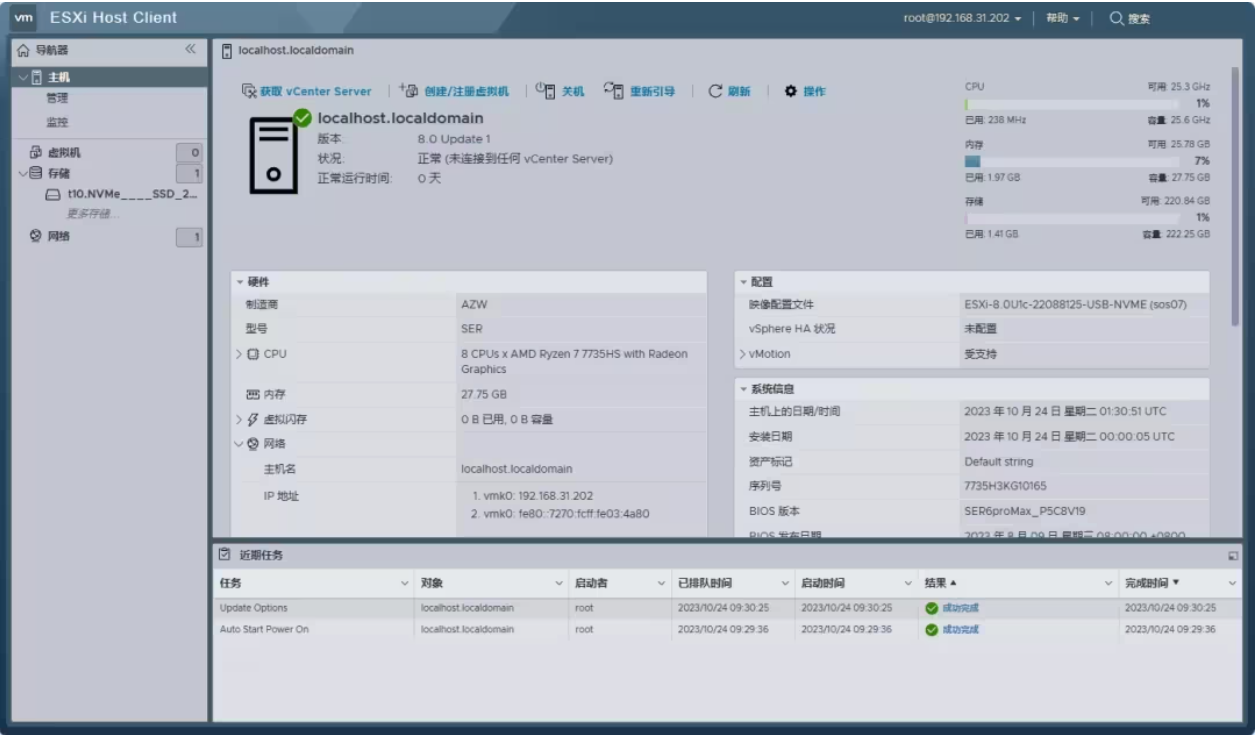
简介:ESXi是VMware公司开发的一款服务器虚拟化操作系统。它能够在一台物理服务器上运行多个虚拟机,每个虚拟机都可以独立运行操作系统和应用程序,而且对硬件配置要求低,系统运行稳定。 准备工具: 1.8G或者8G以上容…...

Vue3实践之全局请求URL配置和请求参数说明
Vue3实践之全局请求URL配置和请求参数说明 全局请求URL配置 1、首先需要导入router和axios import router from "/router";2、创建app,将router挂载到app上 const app createApp(App) app.use(router).use(elementIcons).mount(#app)3、设置全局请求…...
类和对象—初阶
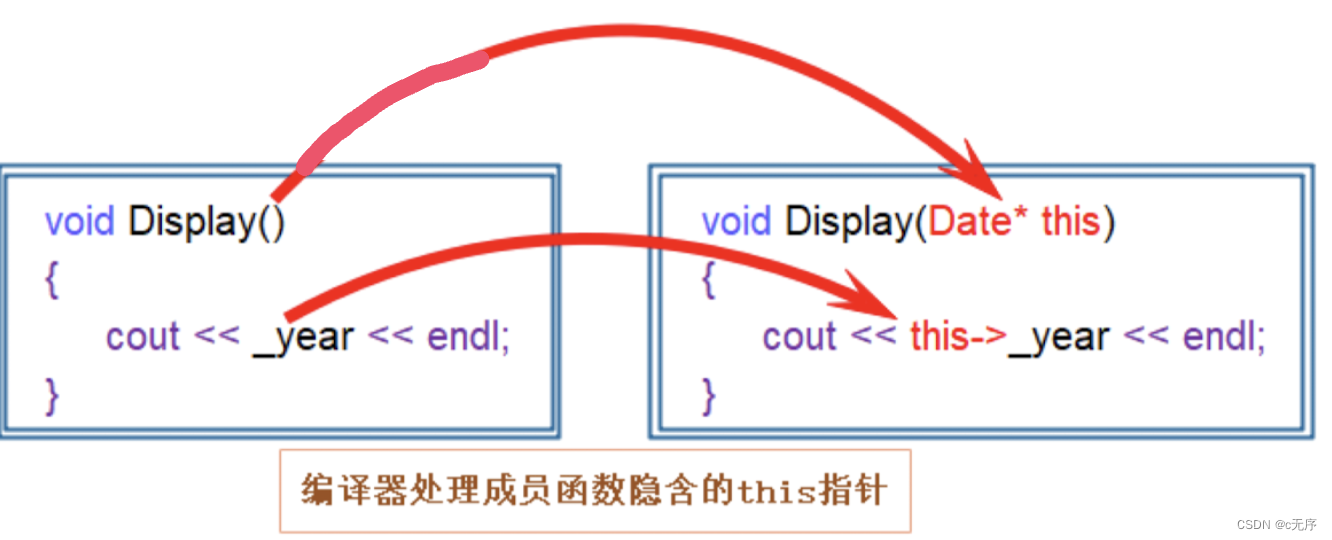
目录 1.面向过程和面向对象初步认识 2.类的引入 3.类的定义 4.类的访问限定符及封装 4.1 访问限定符 【面试题】 4.2 封装 【面试题】 5.类的作用域 6.类的实例化 7.类对象模型 7.1 如何计算类对象的大小 7.2 类对象的存储方式 7.3 结构体内存对齐规则 【面试题】…...

【Linux】shell 脚本基础使用
在终端中输入命令可以完成一些常用的操作,但是我们都是一条一条输入命令,比较麻烦,为了解决这个问题,就会涉及到 shell 脚本,它可以将很多条命令放到一个文件里面,然后直接运行这个文件即可。 shell 脚本类…...

nfs部署--相关记录
以下是在 CentOS 8 中将 10.40.111.41 上的 /nfsdata 目录通过 NFS 共享到 10.40.111.43 和 10.40.111.45 的 /nfsdata 目录的详细步骤: 在 10.40.111.41 上操作: 安装并配置 NFS 服务器: a. 安装 NFS 服务器软件包: sudo dnf in…...
java国产化云HIS基层医院系统源码 SaaS模式
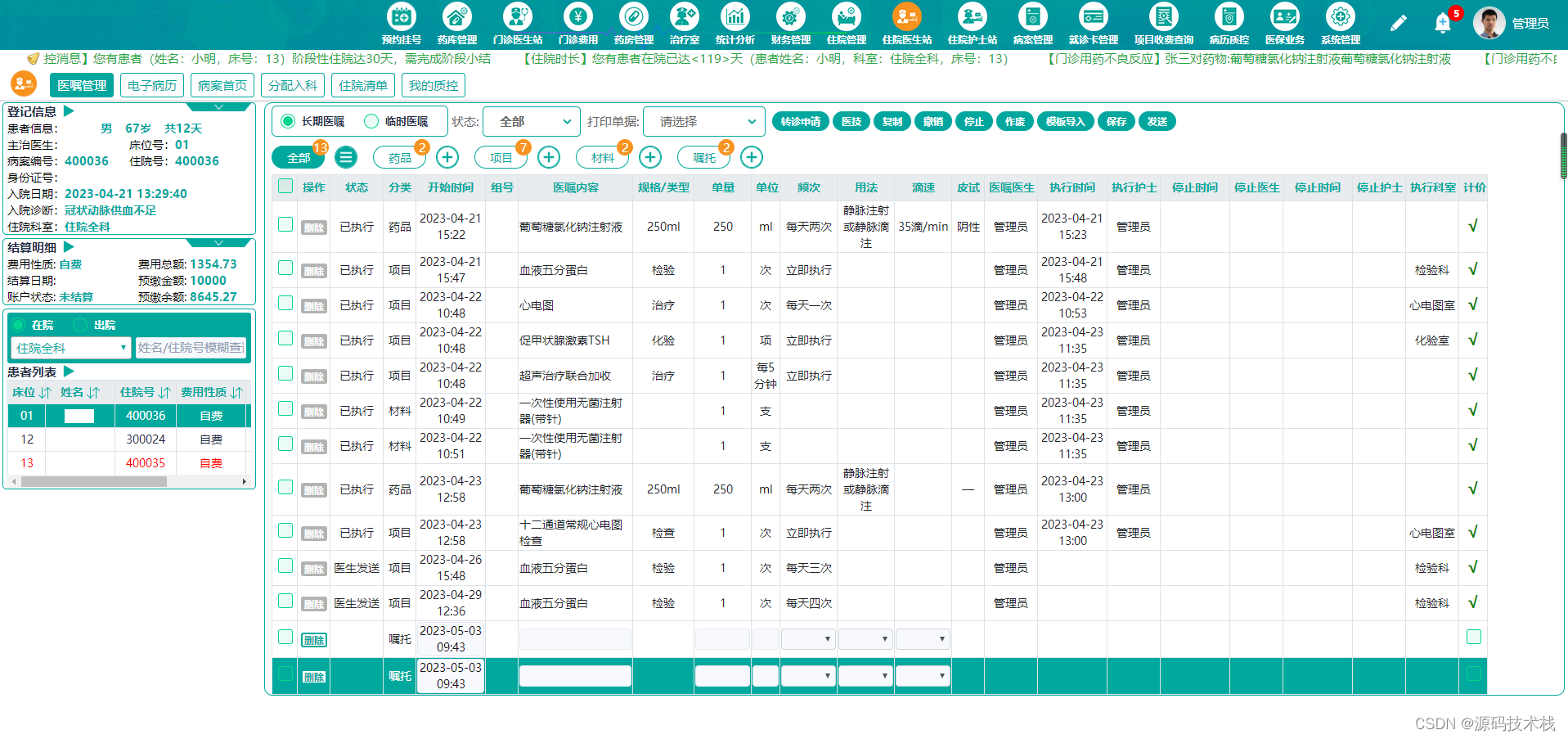
目录 云HIS开发环境 功能模块介绍: 1、门诊模块 2、住院模块 3、药房、药库模块 编辑 4、电子病历模块 5、统计报表模块 6、系统管理模块 系统优势 云his之电子病历子系统功能 云 his 系统是运用云计算、大数据、物联网等新兴信息技术,按…...
docker 部署 Epusdt - 独角数卡 dujiaoka 的 usdt 支付插件
部署 部署说明 部署之前必须注意的几点事项,该教程不一定适合所有用户: 本教程主要是使用 docker 部署,宝塔用户或宿主机直接安装的用户请直接参考官网教程.本教程是独立部署 epusdt,使用独立的mysql和redis,与dujiaoka项目分开. 在研究的过程中发现 epusdt 也需要用到 mys…...
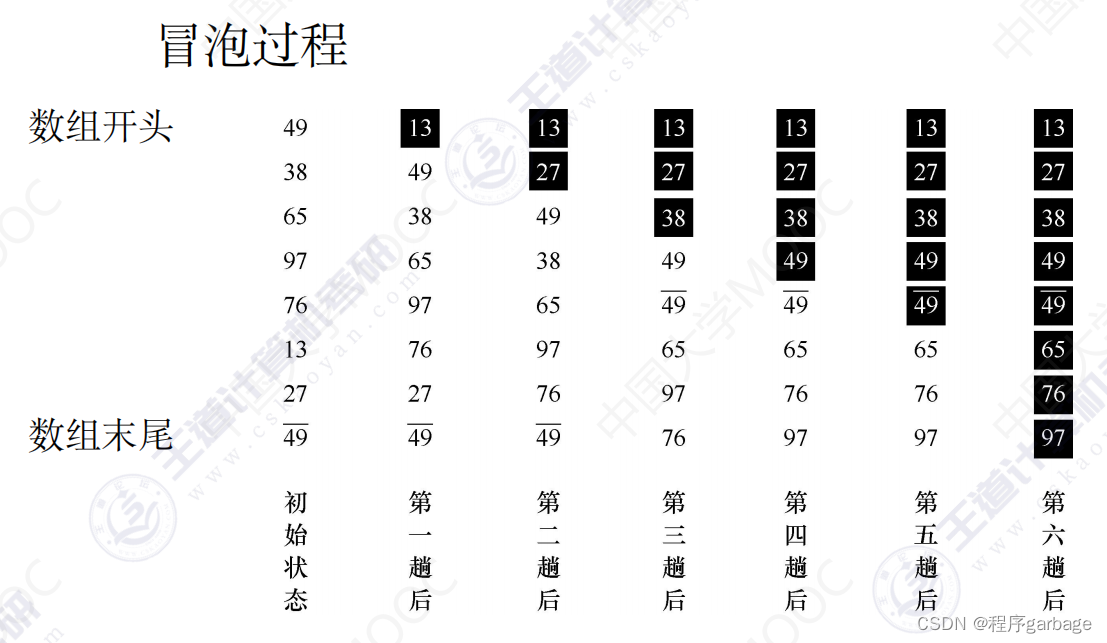
数据结构排序之冒泡、快速、插入、选择、堆、归并等排序及时间,空间复杂度等(超详解,绝对能满足你的需求,并能学到很多有用知识)
在本文章开始之前给大家介绍个网站,可以通过下面动画网址来理解 ,(国外的网站帮助学习数据结构很多知识,可以翻译下来,在搜索框搜索相应的排序算法进行动画演示,非常好用。)https://www.cs.usfca.edu/~galles/visualization/https://www.cs.usfca.edu/~galles/vis…...

如何在windows环境和linux环境运行jar包
功能:实现对字符串小写转大写 java代码如下: package a_od_test;import java.util.Locale; /* 实现小写转大写 打jar包 分别在windows环境和liunx环境运行*/ public class Main28_To_Upper {public static void main(String[] args) {if (args.length 1) {System.out.printl…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...
