在Go语言中使用select和channel来期待确定性行为
Go开发人员在使用channel时常犯的一个错误是,对select在多个channel中的行为方式做出错误的假设。错误的假设可能会导致难以识别和重现的细微错误。假设我们要实现一个需要从两个channel接收消息的goroutine:
我们可能会决定像下面这样处理优先级:
for {select {case v := <-messageCh:fmt.Println(v)case <-disconnectCh:fmt.Println("disconnection, return")return}
}我们使用select从多个channel接收消息。因为我们想优先考虑messageCh,所以可以假设应该首先编写messageCh情况,然后再编写disconnectCh情况。但是这段代码真的有用吗?让我们通过编写一个发送10条消息然后发送断开连接通知的虚拟生产者goroutine来尝试一下:
for i := 0; i < 10; i++ {messageCh <- i
}
disconnectCh <- struct{}{}运行这个例子,如果messageCh被缓冲,下面是一个可能的输出:
0
1
2
3
4
disconnection, return我们只收到了其中的5条。这是什么原因呢?它依赖于具有多个channel的select语句的规范:
相关文章:

在Go语言中使用select和channel来期待确定性行为
Go开发人员在使用channel时常犯的一个错误是,对select在多个channel中的行为方式做出错误的假设。错误的假设可能会导致难以识别和重现的细微错误。假设我们要实现一个需要从两个channel接收消息的goroutine: 我们可能会决定像下面这样处理优先级: for {select {case v := &…...
【MATLAB源码-第19期】matlab基于导频的OFDM系统瑞利信道rayleigh的信道估计仿真,输出估计与未估计误码率对比图。
1、算法描述 正交频分复用(英语:Orthogonal frequency-division multiplexing, OFDM)有时又称为分离复频调制技术(英语:discrete multitone modulation, DMT),可以视为多载波传输的一个特例&am…...

坚持十天做完Python入门编程100题第三天加班
坚持十天做完Python入门编程100题第三天加班 第24题 扫描文件列表第25题 如何将字典转换成JSON并写入json文件?第26题 JSON转换成字典 第24题 扫描文件列表 如何扫描当前目录下的文件列表?解析:可以使用python内置的glob模块,用法…...

MSOLSpray:一款针对微软在线账号(AzureO365)的密码喷射与安全测试工具
关于MSOLSpray MSOLSpray是一款针对微软在线账号(Azure/O365)的密码喷射与安全测试工具,在该工具的帮助下,广大研究人员可以直接对目标账户执行安全检测。支持检测的内容包括目标账号凭证是否有效、账号是否启用了MFA、租户账号是…...
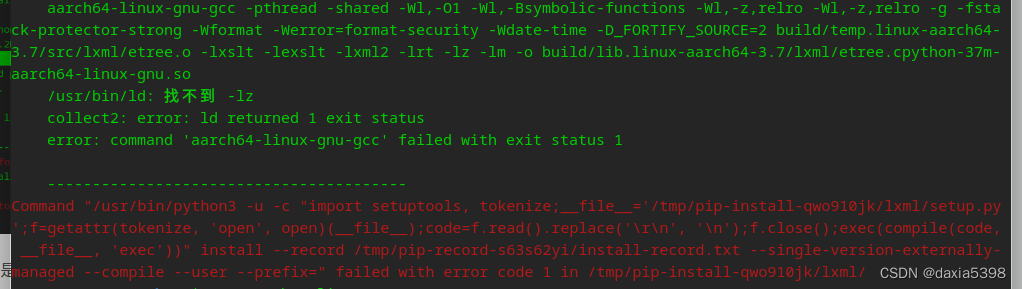
uos安装lxml避坑记录
环境:紫光电脑uos系统 python:系统自带3.7.3 条件:已打开开发者模式,可以自行安装应用商店之外的软件 一、pip3 install lxml4.8.0可以正正常下载,但出现如下错误 另:为什么是4.8.0?因为这个…...
)
518. 零钱兑换 II(力扣LeetCode)
文章目录 518. 零钱兑换 II题目描述动态规划一维数组为什么不能交换两个for循环的顺序? 二维数组 518. 零钱兑换 II 题目描述 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数…...
)
01串的熵(蓝桥杯)
文章目录 01串的熵问题描述答案:11027421题意解释暴力枚举 01串的熵 问题描述 对于一个长度为n的01串 S x 1 x 2 x 3 x_{1}x_{2}x_{3} x1x2x3… x n x_{n} xn,香农信息熵的定义为 H(S) − ∑ 1 n p ( x i ) l o g 2 ( p ( x i ) ) -\sum _{1…...

Rust 基础语法和数据类型
数据类型 Rust提供了一系列的基本数据类型,包括整型(如i32、u32)、浮点型(如f32、f64)、布尔类型(bool)和字符类型(char)。此外,Rust还提供了原生数组、元组…...

【Java SE】10 String类
目录 1. String类的重要性 2.常用方法 2.1字符串构造 2.2 String对象的比较 2.3字符串查找 2.4转化 2.5字符串替换 2.6字符串拆分 2.7字符串截取 2.8其他操作方法 2.9字符串的不可变性 2.10字符串修改 3. StringBuffer和StringBuilder 3.1StringBuilder的介绍 4.…...

web蓝桥杯真题:新鲜的蔬菜
代码: .box {display: flex; } #box1 {align-items: center;justify-content: center; }#box2 {justify-content: space-between; } #box2 .item:nth-child(2) {align-self: end; }#box3 {justify-content: space-between; } #box3 .item:nth-child(2) {align-self…...

超声波清洗机能洗哪些东西?洗眼镜超声波清洗机推荐
在现代生活中,人们对清洁卫生的要求越来越高,尤其是对一些细小物件的清洁。眼镜作为我们日常生活中不可或缺的物品,清洁保养更是至关重要。传统的清洗方式可能无法完全清洁眼镜表面的细菌和污垢,于是超声波清洗机成为了很多人的选…...
)
[C++][算法基础]走迷宫(BFS)
给定一个 nm 的二维整数数组,用来表示一个迷宫,数组中只包含 0 或 1,其中 0 表示可以走的路,1 表示不可通过的墙壁。 最初,有一个人位于左上角 (1,1)(1,1) 处,已知该人每次可以向上、下、左、右任意一个方…...

C语言字符串左旋
一、前言 这个题目的完整题目是这样子的。 二、我们实现这个编程的思路 2.1暴力破解思想 假如有一个数组里面的字符串为”abcdef“,我们这时候就这样先将字符”a“移到最后再将其余的字符前移。 2.2三步移动法 同样我们还是假设一个数组里面存的是字符串”abcd…...

Linux 中断会产生嵌套吗?
文章目录 1. 前言2. Linux 中断是否会嵌套?2.1 分析背景2.2 中断处理抢占、嵌套可能性分析2.3 中断处理抢占、嵌套小结 3. 参考资料 1. 前言 限于作者能力水平,本文可能存在谬误,因此而给读者带来的损失,作者不做任何承诺。 2. …...
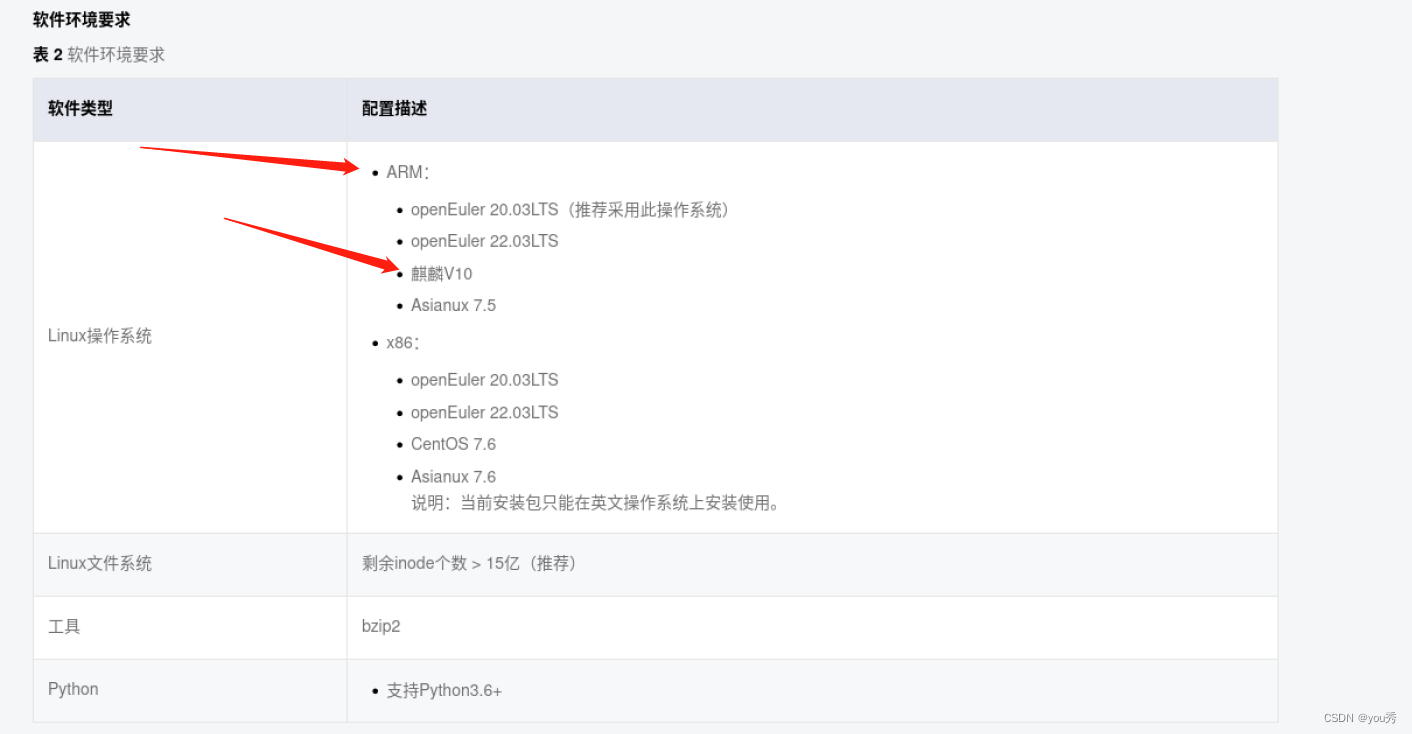
嵌入式ARM版本银河麒麟操作系统V10SP1安装OPenGauss数据库
前言: 官网提供了非常完整的openGauss安装步骤。 https://opengauss.org/zh/download/archive/列举一下个人的使用环境: 麒麟V10 rk3588工控板(ARM) openGauss-3.0.5(极简版)浏览一下官网,可以…...

深度学习八股文
Bert旨在通过联合左侧和右侧的上下文,从未标记文本中预训练出一个深度双向表示模型。因此,BERT可以通过增加一个额外的输出层来进行微调,就可以达到为广泛的任务创建State-of-the-arts 模型的效果,比如QA、语言推理任务。Bert的构…...

jquery 自整理
echarts官方:Documentation - Apache ECharts 1、CheckBox复选框 //选中事件(页面点击) $(#operateExit).on(ifChecked, function(){ $(input[name"operateExit"]).val(1); }); //非选中事件ÿ…...

MySQL | 加索引报错
报错信息 1170 - BLOB/TEXT column user_name used in key specification without a key length解决方案 分析 这个错误通常是因为尝试在一个包含BLOB或TEXT类型列的列上创建索引时没有指定键的长度。MySQL要求在使用BLOB或TEXT类型列作为索引键时,必须指定键的长…...

前端:自制年历
详细思路可以看我的另一篇文章《前端:自制月历》,基本思路一致,只是元素布局略有差异 ①获取起始位startnew Date(moment().format(yyyy-01-01)).getDay() ②获取总的格子数numMath.ceil(365/7)*7,这里用365或者366计算结果都是一样的371 …...

9.手写JavaScript大数相加问题
一、核心思想 找到两个字符串中最长的长度,对两个字符串在头位置补0达到相等的长度,相加时注意进位和类型转换,特别考虑当相加到第一位是如果仍然有进位不要忽略。此外,js中允许使用的最大的数字为 console.log("最大数&qu…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...

uniapp手机号一键登录保姆级教程(包含前端和后端)
目录 前置条件创建uniapp项目并关联uniClound云空间开启一键登录模块并开通一键登录服务编写云函数并上传部署获取手机号流程(第一种) 前端直接调用云函数获取手机号(第三种)后台调用云函数获取手机号 错误码常见问题 前置条件 手机安装有sim卡手机开启…...

【 java 虚拟机知识 第一篇 】
目录 1.内存模型 1.1.JVM内存模型的介绍 1.2.堆和栈的区别 1.3.栈的存储细节 1.4.堆的部分 1.5.程序计数器的作用 1.6.方法区的内容 1.7.字符串池 1.8.引用类型 1.9.内存泄漏与内存溢出 1.10.会出现内存溢出的结构 1.内存模型 1.1.JVM内存模型的介绍 内存模型主要分…...
