保研线性代数复习3
一.基底(Basis)
1.什么是生成集(Generating Set)?什么是张成空间(Span)?
存在向量空间V=(V,+,*),和向量集(xi是所说的列向量),如果每一个属于V的向量都能被A中向量线性组合来表示,那么说明 A 是向量空间 V 的生成集,A的所有线性组合(所有线性组合不同)称为A的张成空间。
如果A张成了线性空间V,写成V=span[A]=span[x1,...,xk]。
2.什么是基底(Basis)?
基底是相对于向量空间来说的,每一个向量空间都拥有一个基底。例如向量空间V,向量空间V的基底B是向量空间V最小的(除了B之外没有B的子集可以张成向量空间V)线性无关的生成集。对于基底B,增加任何其他向量到B中都会让这个向量集合线性相关,所以基底B也称作向量空间V中最大线性无关的集合。
举例:的标准基是(当然不止下面这几个)

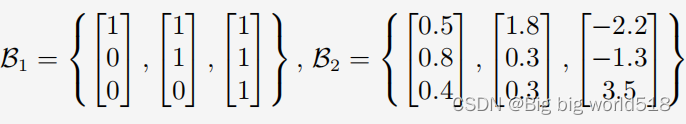
3.如何定义向量空间的维数(dimension)?
对于一个确定的向量空间V,向量空间V的基底中基向量(列向量)的个数是相同的。并且基底中基向量的个数等于向量空间的维数。
4.给定一个矩阵A(n个列向量),A是向量空间V的子集,如何找到A张成的向量空间的基底?
根据行阶梯法找到A中线性无关的向量组合。
5.什么是标准正交基(ONB)?
对于一组基底,如果
,那么称基底B为标准正交基。
标准正交基构成的矩阵Q有的特点:
和
,如果只是正交矩阵的话,那么
二.秩(Rank)
1.什么是矩阵A的秩rk(A)?
矩阵,矩阵A线性无关的行向量的个数=矩阵A线性无关的列向量的个数=rk(A)。
2.矩阵的秩的性质如下:
矩阵A的秩=矩阵A的转置的秩
矩阵的列向量张成一个子空间
,dim(U)=rk(A)
如果矩阵是正则的/可逆的,那么rk(A)=n
线性方程组有解的条件是rk(A)=rk(A|b)
对于,
的解的维数是n-rk(A)
如果满秩,那么rk(A)=min(m,n)
3.矩阵满秩意味着什么?
矩阵满秩=n阶方阵的n阶子式不等于0=n阶方阵的行列式值为0
=如果不是方阵写成行向量或者列向量时线性无关
三.线性映射(Linear Mapping)
1.什么是线性映射?
对于向量空间V和W,存在一种映射称为线性映射并且要满足下面的条件:
![]() 。
。
2.什么是单射双射满射?
单射满射双射都是基于线性映射,满足不同的情况的时候线性映射称为单射满射双射。
单射(injective):![]() 原域中的样本对应目标域中的不同元素。
原域中的样本对应目标域中的不同元素。
满射(surjective):![]() 原域中至少存在一个目标域对应元素,原域中的样本就应该把目标域中的样本对应满。
原域中至少存在一个目标域对应元素,原域中的样本就应该把目标域中的样本对应满。
双射(bijective):单射和满射
3.什么是同构(Isomorpshism)?什么是自同态(Endomorphism)?什么是自同构(Automorphism)?
同构:线性映射and双射,两个有限维度的向量空间同构说明他们的维度相同。如果是同构的,那么
也是同构的。
自同态:,线性
自同构:,线性and双射
4.什么是坐标(coordinate)?
对于一个线性空间V,和向量空间V的有序基底B=(b1,...bn),对于任何一个,我们都能得到一个唯一的线性组合
,这些α1...αn称为是向量x相对于基底B的坐标。如果基底B不同,那么表示一个向量x的坐标不同。
5.什么是转换矩阵(Transformation Matrix)?
对于向量空间V和W,考虑向量空间V的基底和向量空间W的基底
,并且考虑由V到W的线性映射φ,有:

我们称作转换矩阵A,。
6.什么是恒等变换(Identity mapping)?
,称为恒等映射或者恒等自同态。
7.什么是基变换(Basis Change)?
基变换是指在一个向量空间内,由一组基向量变换为另一组基向量,因为在同一个向量空间中,一个点x在不同基底下的坐标不同。若两组基向量不在同一个向量空间中则不能直接进行基变换。一个向量乘以一个方阵说明这个向量在相同空间变换,如果乘以一个矩阵那么说明这个向量在不同空间变换。
8.什么是核(Kernel)和象(Image)?
![]()
![]()
9.什么是秩零化度定理(rank-nullity theorem)?
对于向量空间V和W,存在线性映射,那么dim(ker(φ))+dim(Im(φ))=dim(V)
10.什么是仿射变换(Affine mapping)?
仿射变换=线性变换+平移
对于两个向量空间V和W,存在线性映射,
,那么称作
为从向量空间V到向量空间W的仿射映射。
相关文章:
保研线性代数复习3
一.基底(Basis) 1.什么是生成集(Generating Set)?什么是张成空间(Span)? 存在向量空间V(V,,*),和向量集(xi是所说的列向量ÿ…...

从零开始学Spring Boot系列-集成MyBatis-Plus
在Spring Boot应用开发中,MyBatis-Plus是一个强大且易于使用的MyBatis增强工具,它提供了很多实用的功能,如代码生成器、条件构造器、分页插件等,极大地简化了MyBatis的使用和配置。本篇文章将指导大家如何在Spring Boot项目中集成…...

【云原生篇】k8s之Deployment详解
Kubernetes 的 Deployment 是一种管理声明式更新的资源对象,它允许你描述应用的期望状态,并由 Deployment 控制器自动将当前状态改变为期望状态。Deployment 主要用于无状态应用的部署和扩展,但也可以用于有状态应用。 核心功能 自动化部署…...
linux安装dubboAdmin
1.环境准备: jdk-8u391-linux-x64apache-maven-3.9.6apache-tomcat-8.5.100 2.安装注册中心zookeeper zookeeper的安装看我的另一篇文章,安装完成后保持启动状态 linux安装Zookeeper的详细步骤-CSDN博客 3.安装dubboadmin 源码下载地址:R…...

Android 系统编译 and 应用裁剪
平台应用编译 平台应用demo的Android.mk写法: LOCAL_PATH:= $(call my-dir) include $(CLEAR_VARS)LOCAL_MODULE_TAGS := optional# Only compile source java files in this apk. LOCAL_SRC_FILES := $(call all-java-files-under, src)LOCAL_PACKAGE_NAME := TestLOCAL_CER…...
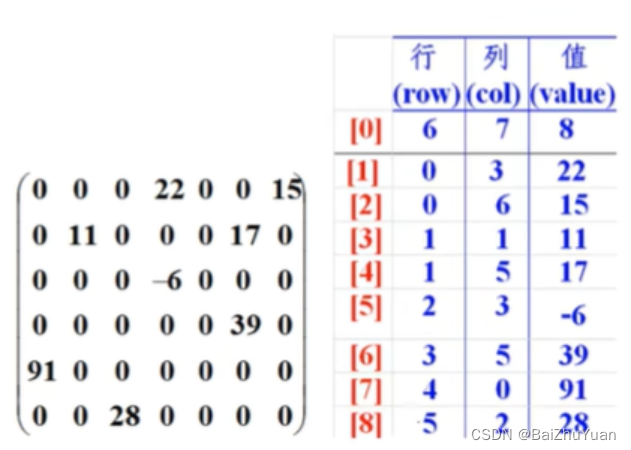
java数组.day16(冒泡排序,稀疏数组)
冒泡排序 冒泡排序无疑是最为出名的排序算法之一,总共有八大排序! 冒泡的代码还是相当简单的,两层循环,外层冒泡轮数,里层依次比较,江湖中人人尽皆知。 我们看到嵌套循环,应该立马就可以得出这个算法的时…...
vue+springboot多角色登录
①前端编写 将Homeview修改为manager Manager: <template><div><el-container><!-- 侧边栏 --><el-aside :width"asideWidth" style"min-height: 100vh; background-color: #001529"><div style"h…...

使用 ADB 查找应用名称和活动名称,并启动指定页面
知识点和难题: 查找应用名称和活动名称: 使用 ADB 命令 adb shell dumpsys window | findstr mCurrentFocus 可以查找当前设备上活动的应用名称和活动名称。 保存输出结果: 将命令的输出结果保存到文件中,方便后续使用。 启动指…...

LangChain - 文档转换
文章目录 一、文档转换器 & 文本拆分器文本拆分器 二、开始使用文本拆分器三、按字符进行拆分四、代码分割 (Split code)1、PythonTextSplitter2、JS3、Markdown4、Latex5、HTML6、Solidity 五、MarkdownHeaderTextSplitter1、动机2、Use case 六、递归按字符分割七、按tok…...

【C++】STL--list
目录 list的介绍 list的使用 list的构造 list iterator的使用 list capacity list modifiers list的迭代器失效 list模拟实现 list的介绍 1. list是可以在常数范围内在任意位置进行插入和删除的序列式容器,并且该容器可以前后双向迭代。 2. list的底层是双向…...

二. CUDA编程入门-双线性插值计算
目录 前言0. 简述1. 执行一下我们的第十个CUDA程序2. Bilinear interpolation3. 代码分析总结参考 前言 自动驾驶之心推出的 《CUDA与TensorRT部署实战课程》,链接。记录下个人学习笔记,仅供自己参考 Note:关于 CUDA 加速双线程插值的内容博主…...

实时计算平台设计方案:913-基于100G光口的DSP+FPGA实时计算平台
基于100G光口的DSPFPGA实时计算平台 一、产品概述 基于以太网接口的实时数据智能计算一直应用于互联网、网络安全、大数据交换的场景。以DSPFPGA的方案,体现了基于硬件计算的独特性能,区别于X86GPU的计算方案,保留了高带宽特性&…...

Glide系列-自定义ModuleLoader
在当今快速发展的移动应用领域,图片的高效加载和显示对于提供流畅用户体验至关重要。Glide作为一款强大的图片加载库,已经成为Android开发者的首选工具之一。但是,你有没有遇到过Glide默认不支持的模型类型,或者需要对图片加载过程…...

设计模式——责任链模式13
责任链模式 每个流程或事物处理 像一个链表结构处理。场景由 多层部门审批,问题分级处理等。下面体现的是 不同难度的问题由不同人进行解决。 设计模式,一定要敲代码理解 传递问题实体 /*** author ggbond* date 2024年04月10日 07:48*/ public class…...

Linux云计算之Linux基础3——Linux系统基础part-2
1、终端、shell、文件理论 1、终端 终端(terminal):人和系统交互的必要设备,人机交互最后一个界面(包含独立的输入输出设备) 物理终端(console):直接接入本机器的键盘设备和显示器虚拟终端(tty):通过软件…...
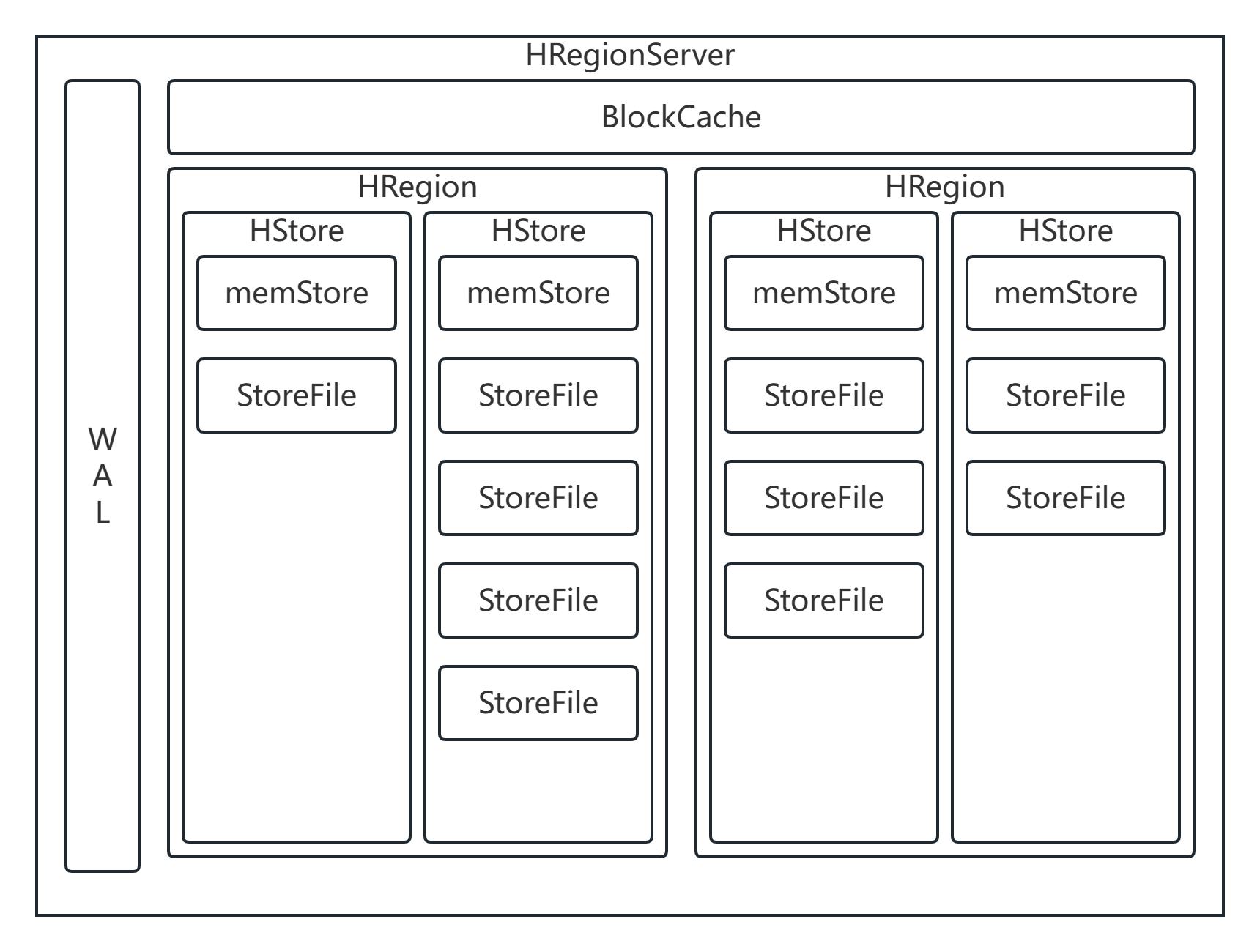
HBase详解(2)
HBase 结构 HRegion 概述 在HBase中,会从行键方向上对表来进行切分,切分出来的每一个结构称之为是一个HRegion 切分之后,每一个HRegion会交给某一个HRegionServer来进行管理。HRegionServer是HBase的从节点,每一个HRegionServ…...
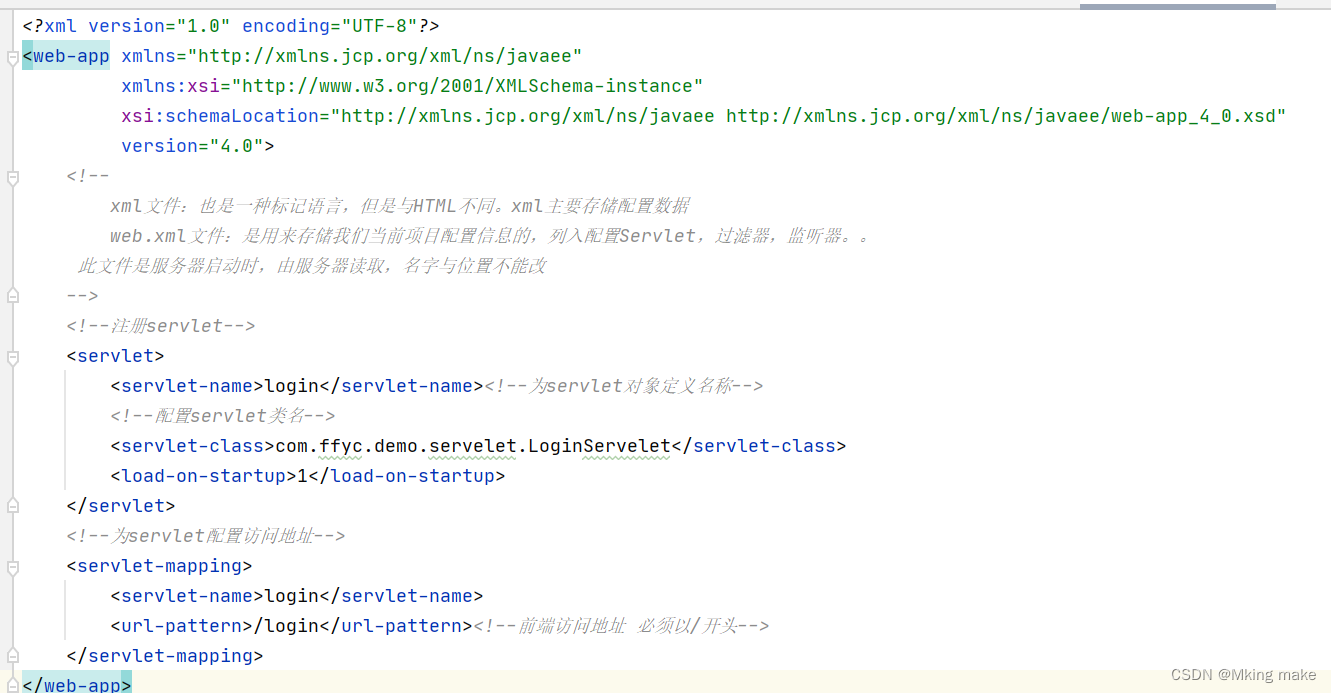
Web后端搭建
目录 一 搭建服务器端 1.1安装服务器软件 1.2检查环境是否配置 1.3安装Tomcat 二 创建并发Web项目 2.1创建一个java项目 三 创建Servlet 前端程序如何才能访问到后端程序呢,这时候我们就需要web服务器来解决:将后端程序部署到服务器中,…...
k8s单节点部署,容器运行时使用containerd
环境 系统 : entOS Linux release 7.9.2009 (CoreIP:192.168.44.177 硬件要求:控制平面最少需要 2c2g 安装前环境准备 如果是集群部署还需要配置时间同步 关闭防火墙 systemctl disable firewalld关闭selinux setenforce 0sed -i s/SELI…...

深入浅出 -- 系统架构之性能优化的核心思维
“在当前的互联网开发模式下,系统访问量日涨、并发暴增、线上瓶颈等各种性能问题纷涌而至,性能优化成为了现时代开发过程中炙手可热的名词,无论是在开发、面试过程中,性能优化都是一个常谈常新的话题”。Java语言作为企业应用中的…...
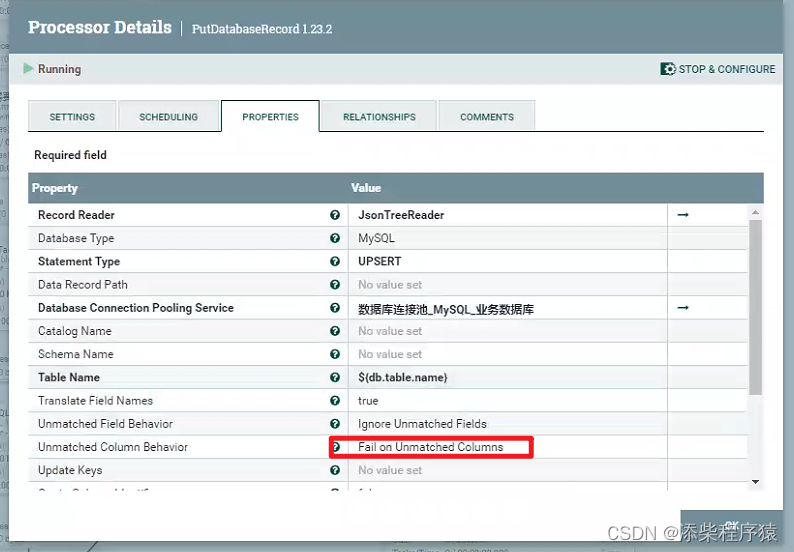
Nifi同步过程中报错create_time字段找不到_实际目标表和源表中没有这个字段---大数据之Nifi工作笔记0066
很奇怪的问题,在使用nifi的时候碰到的,这里是用NIFI,把数据从postgresql中同步到mysql中, 首先postgresql中的源表,中是没有create_time这个字段的,但是同步的过程中报错了. 报错的内容是说,目标表中有个create_time字段,这个字段是必填的,但是传过来的flowfile文件中,的数据没…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...
