当前位置： 首页 > news >正文

LLMs之Morphic：Morphic(一款具有生成式用户界面的人工智能答案引擎)的简介、安装、使用方法之详细攻略

news 2026/2/9 13:08:26

LLMs之Morphic：Morphic(一款具有生成式用户界面的人工智能答案引擎)的简介、安装、使用方法之详细攻略

目录

Morphic的简介

1、技术栈

Morphic的安装和使用方法

1、克隆仓库

2、安装依赖

3、填写密钥

4、本地运行应用

部署

Morphic的简介

2024年4月初发布，Morphic是一款具有生成式用户界面的人工智能答案引擎。

1、技术栈

应用框架：Next.js
文本流处理 / 生成式用户界面：Vercel AI SDK
生成模型：OpenAI
搜索 API：Tavily AI
组件库：shadcn/ui
无头组件原语：Radix UI
样式：Tailwind CSS

Morphic的安装和使用方法

1、克隆仓库

将仓库克隆到您的 Github 账户，然后运行以下命令克隆仓库：

git clone git@github.com:[YOUR_GITHUB_ACCOUNT]/morphic.git

2、安装依赖

cd morphic

bun i

3、填写密钥

cp .env.local.example .env.local

您的 .env.local 文件应如下所示：

用于设置 OpenAI API 请求的基本 URL 路径。

如果需要设置 BASE URL，请取消注释并设置以下内容：

OPENAI_API_BASE=

在此处获取 OpenAI API 密钥：https://platform.openai.com/api-keys

OPENAI_API_KEY=[YOUR_OPENAI_API_KEY]

在此处获取 Tavily API 密钥：https://app.tavily.com/home

TAVILY_API_KEY=[YOUR_TAVILY_API_KEY]

4、本地运行应用

bun dev

您现在可以访问 http://localhost:3000。

部署

使用 Vercel 部署您自己的 Morphic 实时版本。

相关文章：

LLMs之Morphic：Morphic(一款具有生成式用户界面的人工智能答案引擎)的简介、安装、使用方法之详细攻略

LLMs之Morphic：Morphic(一款具有生成式用户界面的人工智能答案引擎)的简介、安装、使用方法之详细攻略 目录 Morphic的简介 1、技术栈 Morphic的安装和使用方法 1、克隆仓库 2、安装依赖 3、填写密钥 4、本地运行应用 部署 Morphic的简介 2024年4月初发布&#xff…...

编程日记 2024/4/13 20:08:49

[react] useState的一些小细节

1.无限循环 因为setState修改是异步的,加上会触发函数重新渲染, 如果代码长这样 一秒再修改,然后重新触发setTImeout, 然后再触发,重复触发循环 如果这样呢 还是会,因为你执行又会重新渲染 2.异步修改数据 为什么修改多次还是跟不上呢? 函数传参解决 因为是异步修改 ,所以…...

编程日记 2024/4/13 20:06:47

蓝桥杯【第15届省赛】Python B组

这题目难度对比历届是相当炸裂的简单了…… A：穿越时空之门 【问题描述】 随着 2024 年的钟声回荡，传说中的时空之门再次敞开。这扇门是一条神秘的通道，它连接着二进制和四进制两个不同的数码领域，等待着勇者们的探索。 在二进制…...

编程日记 2024/4/13 20:05:46

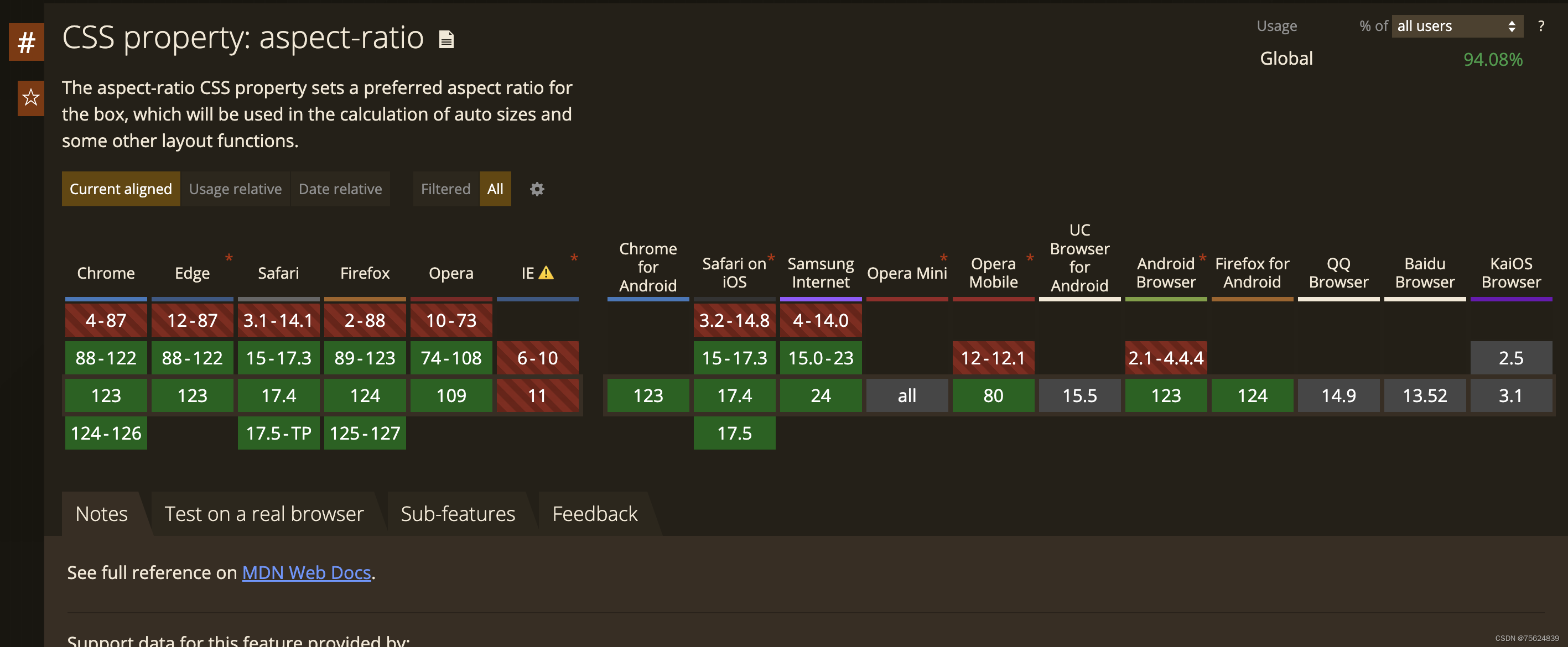
CSS aspect-ratio属性设置元素宽高比

aspect-ratio 是CSS的一个属性&#xff0c;用于设置元素的期望宽高比。它设置确保元素保持特定的比例&#xff0c;不受其内容或容器大小的影响。 语法&#xff1a; aspect-ratio: <ratio>;其中 <ratio> 是一个由斜杠&#xff08;/&#xff09;分隔的两个数字&…...

编程日记 2024/4/13 20:01:42

Jones矩阵符号运算

文章目录 Jones向量Jones矩阵 有关Jones矩阵、Jones向量的基本原理&#xff0c;可参考这个&#xff1a; 通过Python理解Jones矩阵&#xff0c;本文主要介绍sympy中提供的有关偏振光学的符号计算工具 Jones向量 Jones向量是描述光线偏振状态的重要工具&#xff0c;例如一个偏振…...

编程日记 2024/4/13 19:56:34

解决 App 自动化测试的常见痛点！

App 自动化测试中有些常见痛点问题&#xff0c;如果框架不能很好的处理&#xff0c;就可能出现元素定位超时找不到的情况&#xff0c;自动化也就被打断终止了。很容易打消做自动化的热情&#xff0c;导致从入门到放弃。比如下面的两个问题&#xff1a; 一是 App 启动加载时间较…...

编程日记 2024/4/13 19:52:30

2016NOIP普及组真题 1. 买铅笔

线上OJ&#xff1a; 一本通&#xff1a;http://ybt.ssoier.cn:8088/problem_show.php?pid1973 核心思想&#xff1a; 向上取整的代码 (m (n-1))/n 。&#xff08;本题考点与2023年J组的第一和第二题一样&#xff09; 比如需要买31支笔&#xff0c;每包30支&#xff0c;则需要…...

编程日记 2024/4/13 19:49:27

机器学习—数据集（二）

1可用数据集 公司内部 eg:百度 数据接口 花钱 数据集 学习阶段可用的数据集&#xff1a; sklearn:数据量小&#xff0c;方便学习kaggle&#xff1a;80万科学数据&#xff0c;真实数据&#xff0c;数据量大UCI&#xff1a;收录了360个数据集&#xff0c;覆盖科学、生活、经济等…...

编程日记 2024/4/13 19:45:23

华为S5735S核心交换配置实例

以下脚本实现创建vlan2,3&#xff0c;IP划分&#xff0c;DHCP启用&#xff0c;接口划分&#xff0c;ssh,telnet,http,远程登录启用 默认用户创建admin/admin123提示首次登录需要更改用户密码S5735产品手册更多功能配置&#xff0c;移步官网参考手册配置 system-viewsysname t…...

编程日记 2024/4/13 19:43:21

Mysql主从复制安装配置

mysql主从复制安装配置 1、基础设置准备 #操作系统&#xff1a; centos6.5 #mysql版本&#xff1a; 5.7 #两台虚拟机&#xff1a; node1:192.168.85.111&#xff08;主&#xff09; node2:192.168.85.112&#xff08;从&#xff09;2、安装mysql数据库 #详细安装和卸载的步骤…...

编程日记 2024/4/13 19:41:18

【刷题】图论——最小生成树：Prim、Kruskal【模板】

假设有n个点m条边。 Prim适用于邻接矩阵存的稠密图&#xff0c;时间复杂度是 O ( n 2 ) O(n^2) O(n2)&#xff0c;可用堆优化成 O ( n l o g n ) O(nlogn) O(nlogn)。 Kruskal适用于稀疏图&#xff0c;n个点m条边&#xff0c;时间复杂度是 m l o g ( m ) mlog(m) mlog(m)。 Pr…...

编程日记 2024/4/13 19:40:16

使用uniapp实现小程序获取wifi并连接

Wi-Fi功能模块 App平台由 uni ext api 实现&#xff0c;需下载插件&#xff1a;uni-WiFi 链接&#xff1a;https://ext.dcloud.net.cn/plugin?id10337 uni ext api 需 HBuilderX 3.6.8 iOS平台获取Wi-Fi信息需要开启“Access WiFi information”能力登录苹果开发者网站&…...

编程日记 2024/4/13 19:39:15

回忆杀之手搓当年搓过的Transformer

整体代码 import mathimport paddle import paddle.nn as nn import paddle.nn.functional as Fclass MaskMultiHeadAttention(nn.Layer):def __init__(self, hidden_size, num_heads):super(MaskMultiHeadAttention, self).__init__()assert hidden_size % num_heads 0, &qu…...

编程日记 2024/4/13 19:36:13

【AR】使用深度API实现虚实遮挡

遮挡效果 本段描述摘自 https://developers.google.cn/ar/develop/depth 遮挡是深度API的应用之一。 遮挡&#xff08;即准确渲染虚拟物体在现实物体后面&#xff09;对于沉浸式 AR 体验至关重要。 参考下图&#xff0c;假设场景中有一个Andy&#xff0c;用户可能需要放置在包含…...

编程日记 2024/4/13 19:35:11

python-pytorch实现skip-gram 0.5.001

python-pytorch实现skip-gram 0.5.000 数据加载、切词准备训练数据准备模型和参数训练保存模型加载模型简单预测获取词向量画一个词向量的分布图使用词向量计算相似度参考数据加载、切词 按照链接https://blog.csdn.net/m0_60688978/article/details/137538274操作后，可以获得…...

编程日记 2024/4/13 19:33:09

C语言：约瑟夫环问题详解

前言 哈喽&#xff0c;宝子们&#xff01;本期为大家带来一道C语言循环链表的经典算法题&#xff08;约瑟夫环&#xff09;。 目录 1.什么是约瑟夫环2.解决方案思路3.创建链表头结点4.创建循环链表5.删除链表6.完整代码实现 1.什么是约瑟夫环 据说著名历史学家Josephus有过以下…...

编程日记 2024/4/13 19:32:08

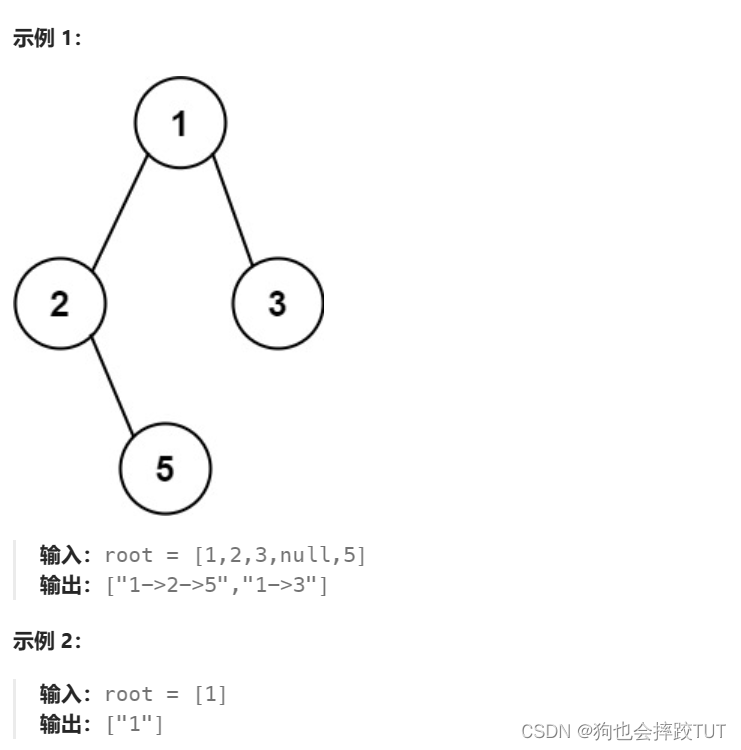
【刷题篇】回溯算法(二)

文章目录 1、求根节点到叶节点数字之和2、二叉树剪枝3、验证二叉搜索树4、二叉搜索树中第K小的元素5、二叉树的所有路径 1、求根节点到叶节点数字之和 给你一个二叉树的根节点 root &#xff0c;树中每个节点都存放有一个 0 到 9 之间的数字。 每条从根节点到叶节点的路径都代表…...

编程日记 2024/4/13 19:29:05

Windows系统本地部署Jupyter Notebook并实现公网访问编辑笔记

文章目录 1.前言2.Jupyter Notebook的安装2.1 Jupyter Notebook下载安装2.2 Jupyter Notebook的配置2.3 Cpolar下载安装 3.Cpolar端口设置3.1 Cpolar云端设置3.2.Cpolar本地设置 4.公网访问测试5.结语 1.前言 在数据分析工作中&#xff0c;使用最多的无疑就是各种函数、图表、…...

编程日记 2024/4/13 19:27:02

自动化运维（二十七）Ansible 实战Shell 插件和模块工具

Ansible 支持多种类型的插件&#xff0c;这些插件可以帮助你扩展和定制 Ansible 的功能。每种插件类型都有其特定的用途和应用场景。今天我们一起学习Shell 插件和模块工具。 一、 Shell 插件 Ansible shell 插件决定了 Ansible 如何在远程系统上执行命令。这些插件非常关键&a…...

编程日记 2024/4/13 19:19:54

Jenkins使用-绑定域控与用户授权

一、Jenkins安装完成后&#xff0c;企业中使用&#xff0c;首先需要绑定域控以方便管理。 操作方法&#xff1a; 1、备份配置文件&#xff0c;防止域控绑定错误或授权策略选择不对&#xff0c;造成没办法登录&#xff0c;或登录后没有权限操作。 [roottest jenkins]# mkdir ba…...

编程日记 2024/4/13 19:18:52

生成xcframework

打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式&#xff0c;可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

编程新知 2025/10/5 2:30:38

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法

树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源&#xff1a; http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作&#xff0c;无需更改相机配置。但是&#xff0c;一…...

编程新知 2026/2/5 4:39:03

ubuntu搭建nfs服务centos挂载访问

在Ubuntu上设置NFS服务器 在Ubuntu上&#xff0c;你可以使用apt包管理器来安装NFS服务器。打开终端并运行&#xff1a; sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享&#xff0c;例如/shared&#xff1a; sudo mkdir /shared sud…...

编程新知 2026/2/6 23:18:59

使用van-uploader 的UI组件，结合vue2如何实现图片上传组件的封装

以下是基于 vant-ui&#xff08;适配 Vue2 版本 &#xff09;实现截图中照片上传预览、删除功能&#xff0c;并封装成可复用组件的完整代码&#xff0c;包含样式和逻辑实现&#xff0c;可直接在 Vue2 项目中使用&#xff1a; 1. 封装的图片上传组件 ImageUploader.vue <te…...

编程新知 2026/1/31 2:37:22

免费PDF转图片工具

免费PDF转图片工具 一款简单易用的PDF转图片工具&#xff0c;可以将PDF文件快速转换为高质量PNG图片。无需安装复杂的软件&#xff0c;也不需要在线上传文件&#xff0c;保护您的隐私。 工具截图 主要特点 &#x1f680; 快速转换&#xff1a;本地转换&#xff0c;无需等待上…...

编程新知 2026/1/26 9:07:56

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】

大家好&#xff0c;我是java1234_小锋老师&#xff0c;看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】&#xff0c;分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...

编程新知 2026/1/29 5:39:49

【网络安全】开源系统getshell漏洞挖掘

审计过程&#xff1a; 在入口文件admin/index.php中&#xff1a; 用户可以通过m,c,a等参数控制加载的文件和方法&#xff0c;在app/system/entrance.php中存在重点代码&#xff1a; 当M_TYPE system并且M_MODULE include时&#xff0c;会设置常量PATH_OWN_FILE为PATH_APP.M_T…...

编程新知 2026/1/31 2:59:25

脑机新手指南（七）：OpenBCI_GUI：从环境搭建到数据可视化（上）

一、OpenBCI_GUI 项目概述 &#xff08;一&#xff09;项目背景与目标 OpenBCI 是一个开源的脑电信号采集硬件平台&#xff0c;其配套的 OpenBCI_GUI 则是专为该硬件设计的图形化界面工具。对于研究人员、开发者和学生而言&#xff0c;首次接触 OpenBCI 设备时&#xff0c;往…...

编程新知 2026/2/3 4:26:32

【前端异常】JavaScript错误处理：分析 Uncaught (in promise) error

在前端开发中&#xff0c;JavaScript 异常是不可避免的。随着现代前端应用越来越多地使用异步操作&#xff08;如 Promise、async/await 等&#xff09;&#xff0c;开发者常常会遇到 Uncaught (in promise) error 错误。这个错误是由于未正确处理 Promise 的拒绝&#xff08;r…...

编程新知 2026/1/1 23:11:45

tomcat指定使用的jdk版本

说明 有时候需要对tomcat配置指定的jdk版本号&#xff0c;此时&#xff0c;我们可以通过以下方式进行配置 设置方式 找到tomcat的bin目录中的setclasspath.bat。如果是linux系统则是setclasspath.sh set JAVA_HOMEC:\Program Files\Java\jdk8 set JRE_HOMEC:\Program Files…...

编程新知 2025/6/10 21:11:28