当前位置： 首页 > news >正文

数学基础：矩阵

news 2026/2/7 10:20:31

来自: https://www.shuxuele.com/algebra/matrix-determinant.html

一、矩阵的行列式

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

在这里插入图片描述

二、矩阵简单知识

在这里插入图片描述
在这里插入图片描述

在这里插入图片描述
在这里插入图片描述

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

三、矩阵乘法

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

四、单位矩阵

在这里插入图片描述

五、逆矩阵一：简单2阶矩阵求法

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

六、逆矩阵二：3、4阶逆矩阵求法

在这里插入图片描述

6.1 求余子式矩阵

在这里插入图片描述在这里插入图片描述

6.2 求代数余子式矩阵

在这里插入图片描述

6.3 求伴随矩阵

在这里插入图片描述

6.4 乘以 1/行列式，得最终结果

在这里插入图片描述
在这里插入图片描述

相关文章：

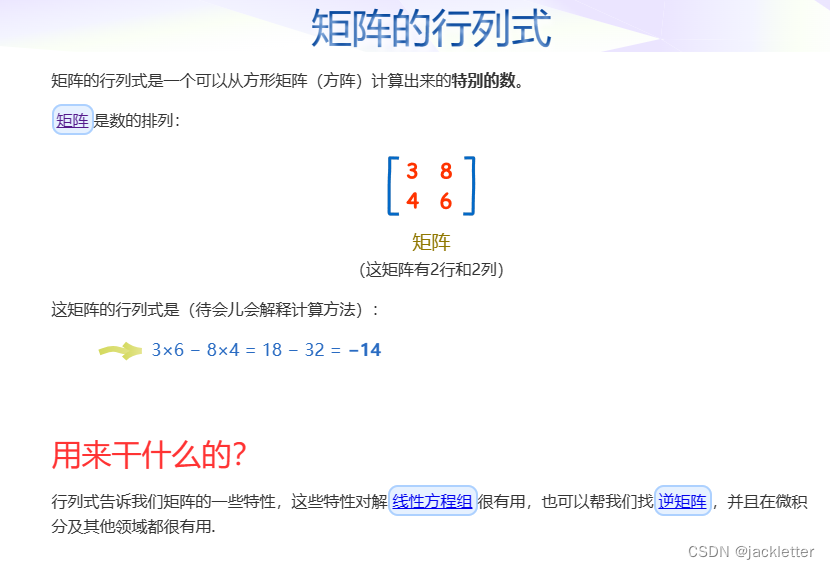
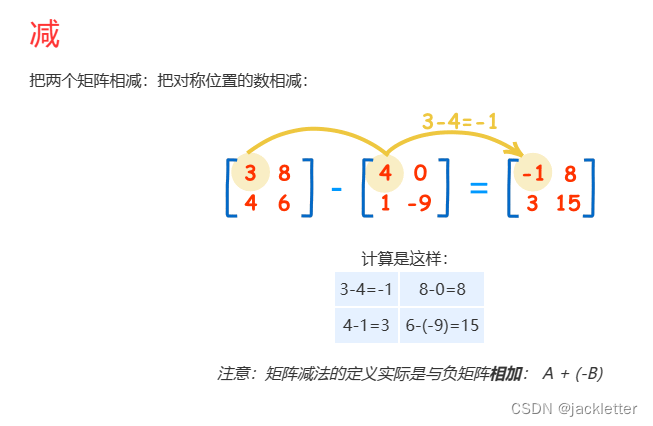
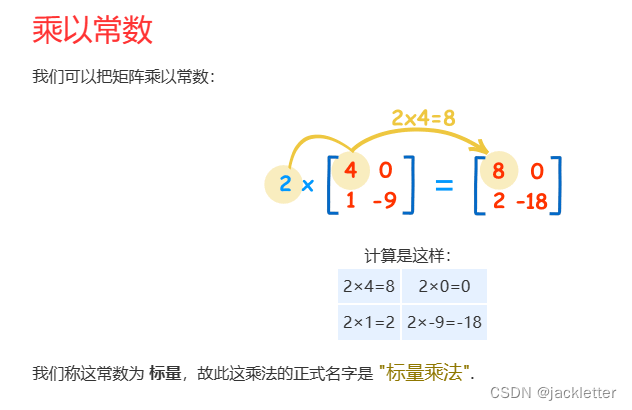
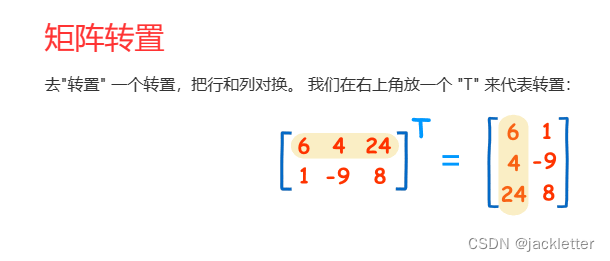
数学基础：矩阵

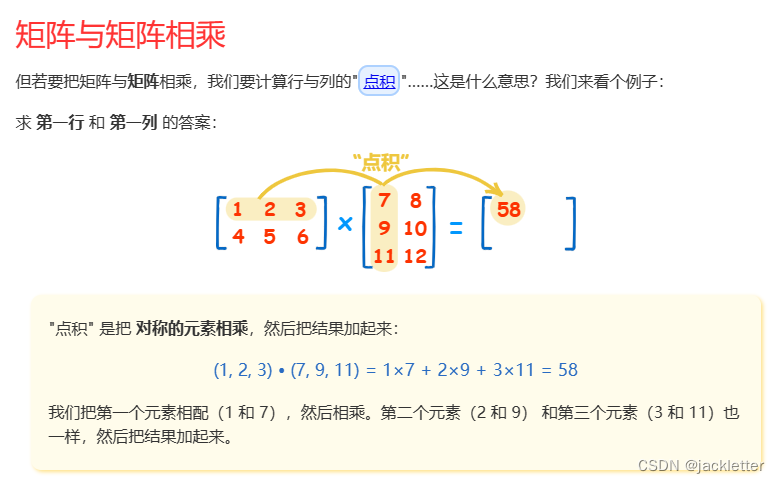
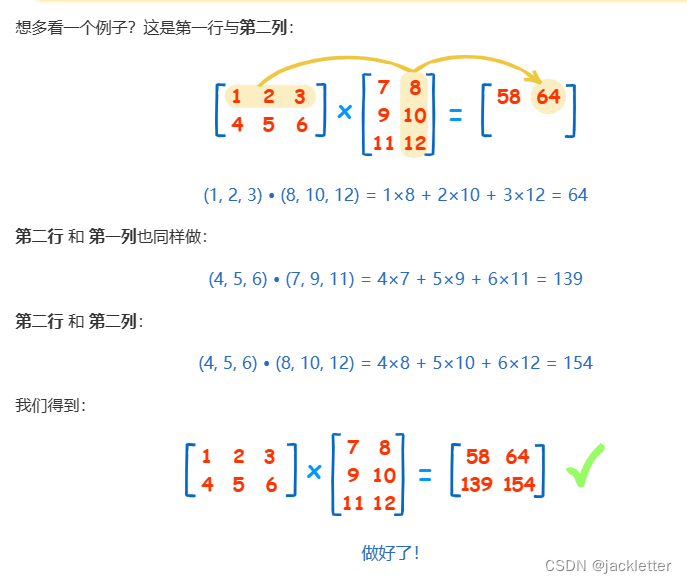
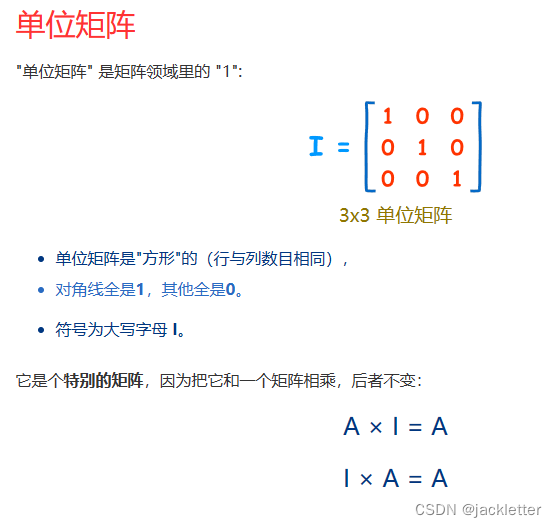
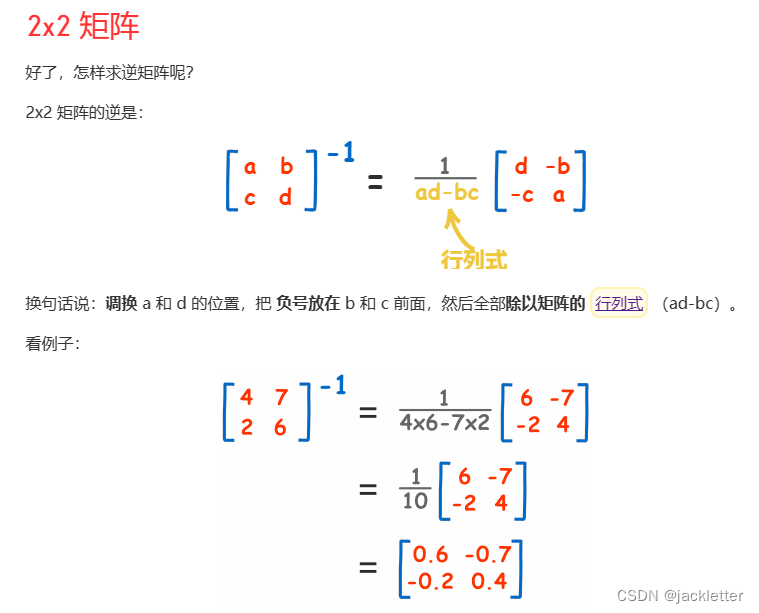
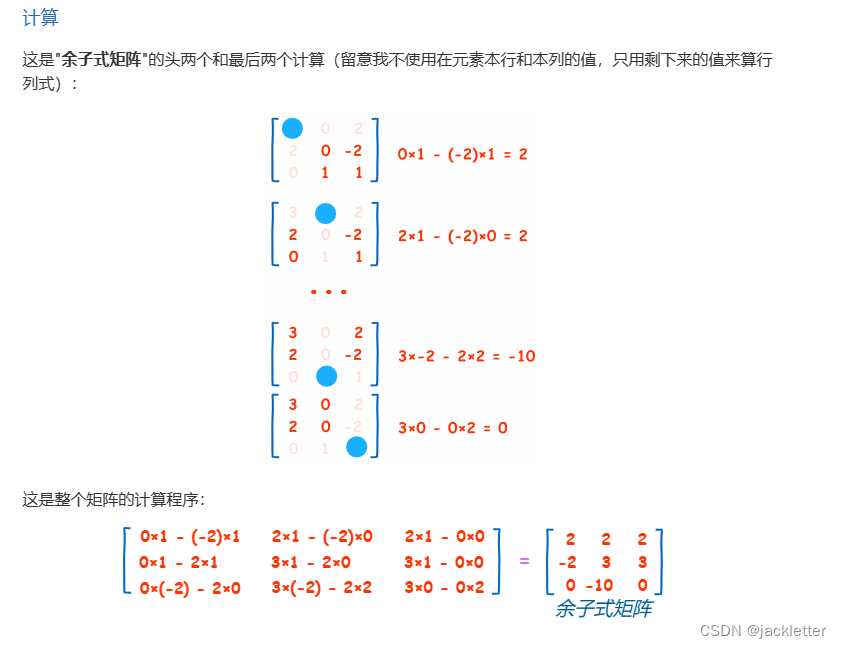
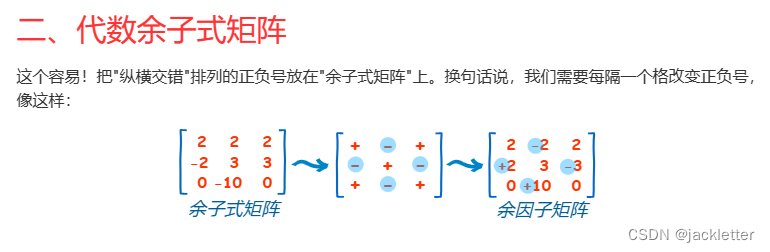
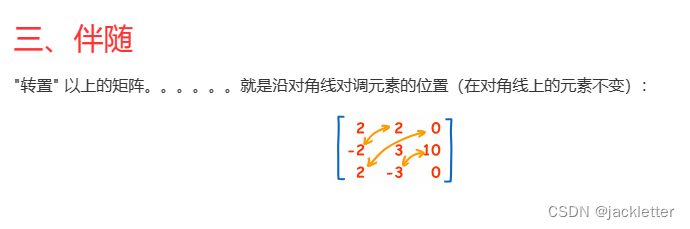
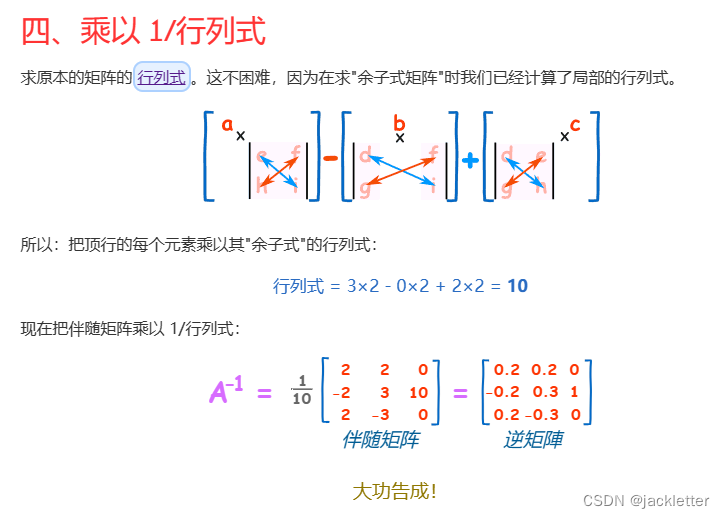
来自: https://www.shuxuele.com/algebra/matrix-determinant.html 一、矩阵的行列式 二、矩阵简单知识 三、矩阵乘法 四、单位矩阵 五、逆矩阵一：简单2阶矩阵求法 六、逆矩阵二：3、4阶逆矩阵求法 6.1 求余子式矩阵 6.2 求代数余子式矩阵 6.3 求伴随矩阵…...

编程日记 2024/4/14 1:45:25

Windows完全卸载MySQL后再下载安装（附安装包）

目录 友情提醒第一章：如何完全卸载干净mysql教程（三个步骤完全卸载）1）步骤一：卸载程序2）步骤二：删除文件3）步骤三：删除注册表信息 第二章：下载软件两种方式1&…...

编程日记 2024/4/14 1:44:24

【央国企专场】——国家电网

国家电网目录 一、电网介绍1、核心业务2、电网组成 二、公司待遇三、公司招聘1、招聘平台2、考试安排2.3 考试内容 一、电网介绍 1、核心业务 国家电网公司（State Grid Corporation of China，简称SGCC）是中国最大的国有企业之一&#xff0c…...

编程日记 2024/4/14 1:43:23

linux 安装MySQL

一、安装mysql 1. 先上传mysql的安装包 使用 rz上传图中的两个rpm包即可 上传的目录: /export/software 2. 卸载linux原生的mysql rpm -qa | grep mysql 如果能看到上图中的mysql-lib…,说明已经安装了，需将其卸载，如：…...

编程日记 2024/4/14 1:42:22

行云防水堡-打造企业数据安全新防线

企业数据安全，顾名思义就是通过各种手段或者技术或者工具保障企业数据的安全性；保障数据信息的硬件、软件及数据受到保护，不受偶然的或者恶意的原因而遭到破坏、更改、泄露，系统连续可靠正常地运行，信息服务不中断。目…...

编程日记 2024/4/14 1:40:20

在ORACLE中找出某列非数字类型的数据

在ORACLE中找出某列非数字类型的数据 使用正则表达式判断非数字值 在Oracle中，我们可以使用正则表达式来判断一个值是否为非数字。正则表达式提供了一种强大的模式匹配和搜索功能，通过匹配数字字符来判断是否为数字。以下是使用正则表达式判断非数字值的…...

编程日记 2024/4/14 1:39:18

建造者模式：构造复杂对象的艺术

在面向对象的设计中，建造者模式是一种重要的创建型设计模式，专门用来构建复杂的对象。它主要目的是将对象的构造代码与其表示代码分离，使同样的构建过程可以创建不同的表示。本文将详细介绍建造者模式的定义、实现、应用场景以及优缺点&#…...

编程日记 2024/4/14 1:37:16

Fence同步

在《Android图形显示系统》没有介绍到帧同步的相关概念，这里简单介绍补充一下。 在图形显示系统中，图形缓存GraphicBuffer可以被不同的硬件来访问，如CPU、GPU、HWC都可以对缓存进行读写，如果同时对图形缓存进行操作，有…...

编程日记 2024/4/14 1:36:15

【UE 委托】如何利用函数指针理解委托的基本原理

目录 0 引言1 函数指针模拟多播委托 🙋‍♂️ 作者：海码007📜 专栏：UE虚幻引擎专栏💥 标题：【UE 委托】如何利用函数指针理解委托的基本原理❣️ 寄语：书到用时方恨少，事非经过不知难…...

编程日记 2024/4/14 1:35:14

【云原生篇】K8S部署全面指南

部署Kubernetes（K8s）有多种方式，可以根据组织的需求、基础设施和资源来选择最合适的部署方法。以下是一些主流的Kubernetes部署方式： 1. 手动部署 kubeadm：Kubernetes官方提供的工具，可以帮助你快速部署和…...

编程日记 2024/4/14 1:33:10

uni-app + vue3实现input输入框保留2位小数的2种方案

首先说明输入框中的格式限制如下： （1）当第一位为0时，第二位只能输入小数点，且不能输入其他数字（如00） （2）当第一位不为0时，后边不限制 （3&…...

编程日记 2024/4/14 1:31:08

原型模式：复制对象的智能解决方案

在软件开发过程中，对象的创建可能是一个昂贵的操作，特别是当对象的初始化包括从数据库加载数据、进行IO操作或进行复杂计算时。原型模式是一种创建型设计模式，它通过复制现有的实例来创建新的对象实例，从而避免了类初始化时的高成…...

编程日记 2024/4/14 1:30:07

量子信息产业生态研究（一）：关于《量子技术公司营销指南（2023）》的讨论

写在前面。量子行业媒体量子内参（Quantum Insider）编制的《量子技术公司营销指南》是一本实用的英文手册，它旨在帮助量子科技公司建立有效的营销策略，同时了解如何将自己定位成各自的行业专家。本文对这篇指南的主要内容进行了翻译…...

编程日记 2024/4/14 1:26:02

vue开发工具和开发环境，测试环境等

Vue.js 的开发主要依赖于一些核心的工具和技术，它们共同构建了一个强大的开发环境，使开发者能够高效地创建和管理 Vue 应用程序。以下是一些主要的 Vue.js 开发工具和资源： 文本编辑器：如 Visual Studio Code (VS Code)&#xff…...

编程日记 2024/4/14 1:25:00

C++---vector容器

是STL容器中的一种常用的容器，由于其大小(size)可变，常用于数组大小不可知的情况下来替代数组。vector容器与数组十分相似，被称为动态数组。时间复杂度为O（1）。 数组数据通常存储在栈中，vector数据通常存储…...

编程日记 2024/4/14 1:19:56

面向电力行业定制安全云工作站解决方案，麒麟信安出席2024年电力企业信创替代技术研讨会

日前，由中国电子企业协会主办的“2024年电力企业信创替代技术研讨会”在江苏南京正式召开。会议以国家推进实现自主可控、加快建设“数字中国”为大背景，聚焦电力企业紧抓“信创替代”机遇，通过安全可靠的软硬件迭代升级，实现企业…...

编程日记 2024/4/14 1:18:55

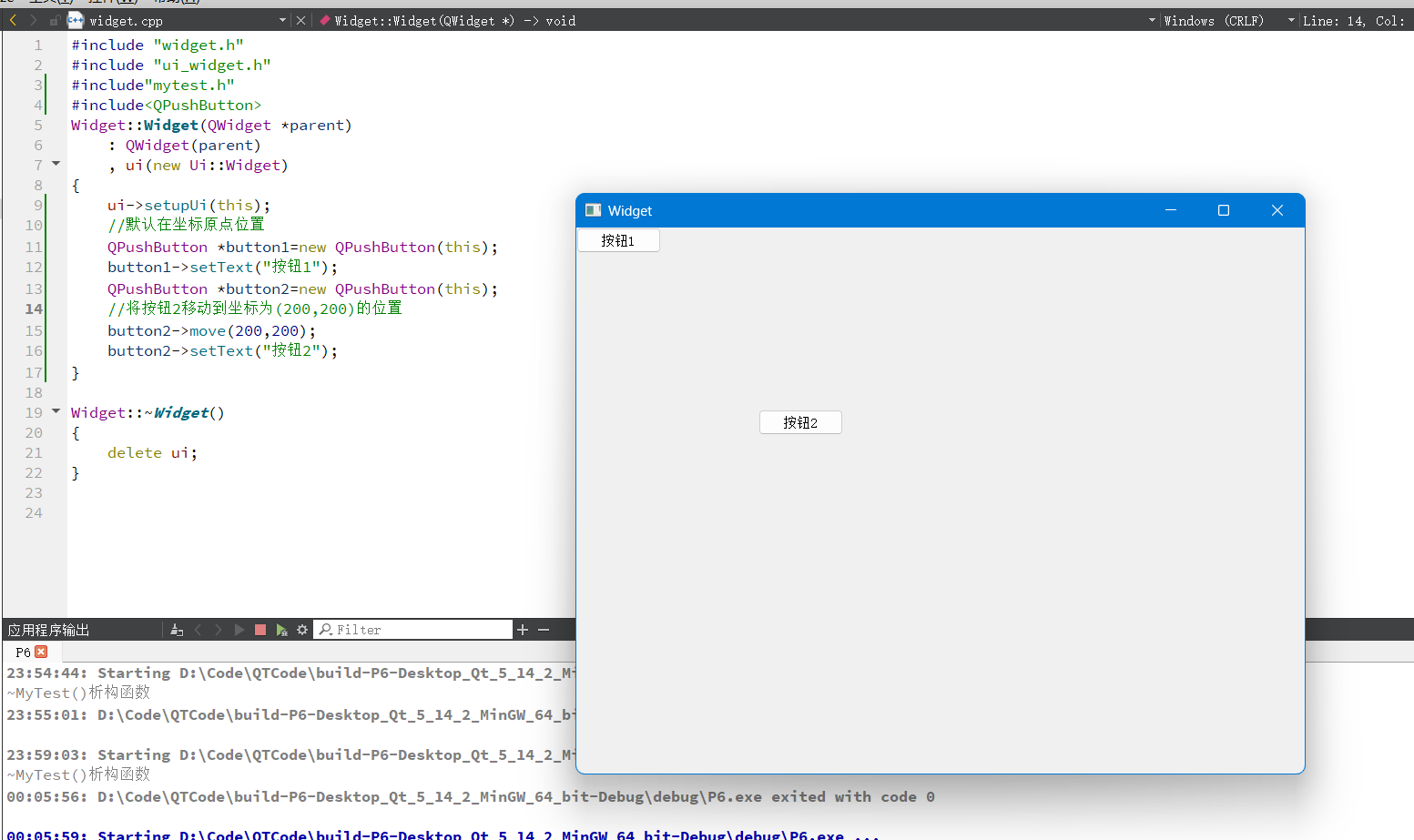
初识 QT

初始QT 什么是QTQT发展史QT支持的平台QT的优点QT的应用场景搭建QT开发环境QT的开发工具概述QT下载安装 使用QT创建项目QT 实现Hello World程序使用按钮控件来实现使用标签控件来实现 项目文件解析widget.hmain.cppwidget.cppwidget.ui.pro文件 对象树QT 窗口坐标体系 什么是QT …...

编程日记 2024/4/14 1:17:54

4. Django 探究FBV视图

4. 探究FBV视图 视图(Views)是Django的MTV架构模式的V部分, 主要负责处理用户请求和生成相应的响应内容, 然后在页面或其他类型文档中显示. 也可以理解为视图是MVC架构里面的C部分(控制器), 主要处理功能和业务上的逻辑. 我们习惯使用视图函数处理HTTP请求, 即在视图里定义def…...

编程日记 2024/4/14 1:15:48

二手车价格预测第十三名方案总结

代码开源链接：GitHub - wujiekd/Predicting-used-car-prices: 阿里天池与Datawhale联合举办二手车价格预测比赛：优胜奖方案代码总结 比赛介绍 赛题以二手车市场为背景，要求选手预测二手汽车的交易价格，这是一个典型的回归问题。…...

编程日记 2024/4/14 1:14:47

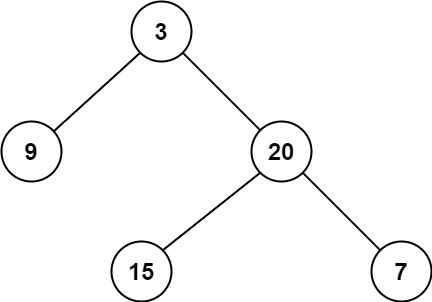
力扣刷题 二叉树层序遍历相关题目II

NO.116 填充每个节点的下一个右侧节点指针 给定一个 完美二叉树 ，其所有叶子节点都在同一层，每个父节点都有两个子节点。二叉树定义如下： struct Node {int val;Node *left;Node *right;Node *next; } 填充它的每个 next 指针，…...

编程日记 2024/4/14 1:13:46

云计算——弹性云计算器（ECS）

弹性云服务器：ECS 概述 云计算重构了ICT系统，云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台，包含如下主要概念。 ECS（Elastic Cloud Server）：即弹性云服务器，是云计算…...

编程新知 2025/8/16 21:50:27

遍历 Map 类型集合的方法汇总

1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

编程新知 2026/1/24 15:08:45

Linux云原生安全：零信任架构与机密计算

Linux云原生安全：零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言：云原生安全的范式革命 随着云原生技术的普及，安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测，到2025年，零信任架构将成为超…...

编程新知 2025/8/17 17:11:47

Module Federation 和 Native Federation 的比较

前言 Module Federation 是 Webpack 5 引入的微前端架构方案，允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

编程新知 2026/1/31 13:48:37

QT： `long long` 类型转换为 `QString` 2025.6.5

在 Qt 中，将 long long 类型转换为 QString 可以通过以下两种常用方法实现： 方法 1：使用 QString::number() 直接调用 QString 的静态方法 number()，将数值转换为字符串： long long value 1234567890123456789LL; …...

编程新知 2026/2/1 6:30:04

Springboot社区养老保险系统小程序

一、前言 随着我国经济迅速发展，人们对手机的需求越来越大，各种手机软件也都在被广泛应用，但是对于手机进行数据信息管理，对于手机的各种软件也是备受用户的喜爱，社区养老保险系统小程序被用户普遍使用，为方…...

编程新知 2026/1/26 2:48:53

Java数值运算常见陷阱与规避方法

整数除法中的舍入问题 问题现象 当开发者预期进行浮点除法却误用整数除法时，会出现小数部分被截断的情况。典型错误模式如下： void process(int value) {double half = value / 2; // 整数除法导致截断// 使用half变量 }此时...

编程新知 2026/2/4 13:10:38

LRU 缓存机制详解与实现（Java版） + 力扣解决

📌 LRU 缓存机制详解与实现（Java版） 一、📖 问题背景 在日常开发中，我们经常会使用 缓存（Cache） 来提升性能。但由于内存有限，缓存不可能无限增长，于是需要策略决定&am…...

编程新知 2025/11/28 20:47:33

GO协程(Goroutine)问题总结

在使用Go语言来编写代码时，遇到的一些问题总结一下 [参考文档]：https://www.topgoer.com/%E5%B9%B6%E5%8F%91%E7%BC%96%E7%A8%8B/goroutine.html 1. main()函数默认的Goroutine 场景再现： 今天在看到这个教程的时候，在自己的电…...

编程新知 2026/1/31 6:53:53

逻辑回归暴力训练预测金融欺诈

简述 「使用逻辑回归暴力预测金融欺诈，并不断增加特征维度持续测试」的做法，体现了一种逐步建模与迭代验证的实验思路，在金融欺诈检测中非常有价值，本文作为一篇回顾性记录了早年间公司给某行做反欺诈预测用到的技术和思路。百度…...

编程新知 2026/1/30 5:02:17