2022年蓝桥杯省赛软件类C/C++B组----积木画
想借着这一个题回顾一下动态规划问题的基本解法,让解题方法清晰有条理,希望更多的人可以更轻松的理解动态规划!
目录
【题目】
【本题解题思路】
【DP模版】
总体方针:
具体解题时的套路:
【题目】
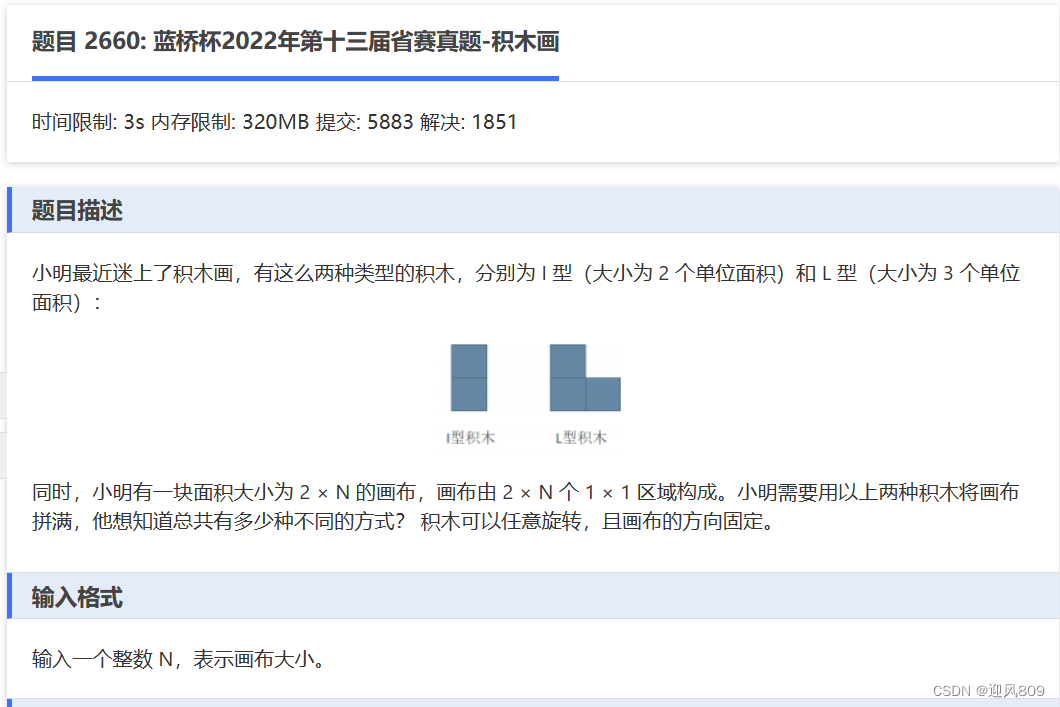
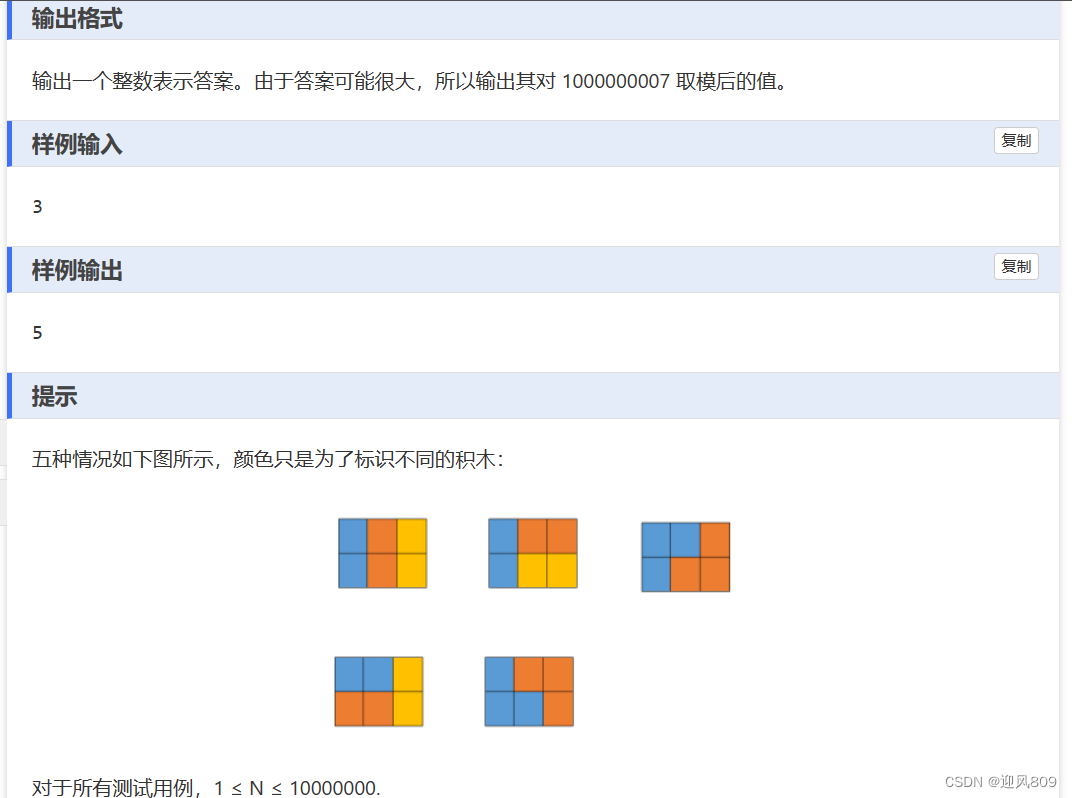
【本题解题思路】
———类似题目:覆盖墙壁 - 洛谷(很多经典题解在里面)
1、确定子状态:
我最终要求解的是:用两种类型的积木将2 x n的画卷填满时有着多少种组合方案。(围绕最终要求解的问题确定子问题)
所以子问题应该是在长度为n的情况下有多少种解法。
所以用一维数组dp[i] 存储长度为i 时的方案数。
2、确定转移的边界情况和初始状态:
这里先正着推,已知n=3时dp[3]=5,那么就可以先明确n=1,n=2时对应的dp[i],即dp[1]=1,dp[2]=2;
然后发现没有什么明显的规律呢,那就再倒着来
3、确定状态转移方式:
为了方便表述,设画卷长度为len;
我想知道画卷长度为len=n时的值,那么我就找他的上一层 len=n-1时的状态,看看有没有什么关联。为了形成填满画卷的状态,我的最后一块位置可以怎么摆放积木呢,从积木的两种类型出发,发现他可以形成四种状态。这里用分类的思想将所有的选择罗列出来,找规律。
如图所示,最后一次有如下选择:
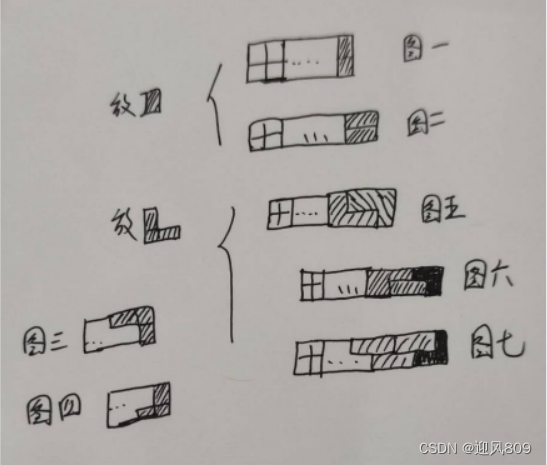
(1)最后一次选竖着的I ,那么dp[n]=dp[n-1]。
因为最后一位固定好了就这一种选择,即1*dp[n-1]。如图1;
(2)最后一次选横着的I ,那么为了填补上画卷,第二行也只能选横着的I 这两个横着的I作为一个整体是一种填补画卷的方式。此时dp[n]=dp[n-2];
如图2所示。
前两种状态都很明显,但是如果选用L形的怎么罗列呢:
(3)L型垂直翻转前后算两种状态,如图3、4. 下面仅根据其中的一种情况来讨论,最后因为翻转所有的结果×2 即可。
A.可以用两个L形成长度为3的整体来填补画卷,dp[n]=dp[n-3],如图5;
B.采用两个L和一个横着的I的方式形成一个整体作为一种方法填补,dp[n]=dp[n-4],如图6;
C.同上,还可以采用在两侧两个L中间包裹多个横着的I的方式来填补,每多一个横着的I相当于这个用于填补的图像整体的长度+1。所以类推得到dp[n]=dp[n-5],dp[n-6],... 如图7;
综上所述,形成填满画卷的前一个整体的状态可以采用如上这些方式,所以他的方案总数就有:
dp[n]=dp[n-1]+dp[n-2]+2*(dp[n-3]+dp[n-4]+...dp[0]);
假如用前缀和sum[n]表示前n个长度的方案总和,dp[n]=sum[n-1]+sum[n-3];
但是我这里只求了n=1---3的情况,n=4时情况虽然有点复杂,但是也还是不好求(哈哈)。
所以有没有什么化简的方式呢,大家记不记得高考时第一个大题考的数组的性质,这里就可以用来变换公式;
dp[n]=sum[n-1]+sum[n-3];
dp[n-1]=sum[n-2]+sum[n-4];
上下相减发现 dp[n]-dp[n-1]=dp[n-1]+dp[n-3];
所以,dp[n]=2*dp[n-1]+dp[n-3]
这就把递推公式推出来了,完美撒花!
【DP模版】
总体方针:
凡是动态规划问题,可以从以下三个角度考虑,确定求解问题的基本思路:
(有时是二维问题或者多维问题时可以考虑用二维或者多维数组)

动态规划问题具有两个性质:
(1)无后效性:每个子问题的解都是基于之前子问题的解,而不受后续子问题解的影响。这意味着我们可以独立地解决每个子问题,然后将这些解组合起来形成一个最优解。即当前状态的解只受此状态之前(就是过去的状态)的影响,一经确定,未来的状态不影响当前状态的结果。
(换成人话就是,当前状态的结果是由之前状态形成的,一旦确定,后续的状态对他没有影响)
(2)子问题重叠性:每个子问题之间类似于嵌套的关系,我想求这个子问题,就必须先解决比他规模更小的、具有同样规律的子问题。
具体解题时的套路:
1、按照题目的求解问题,确定子问题是什么,把存储每个子问题的数据结构定义出来;
2、根据题目中给的信息,自己推理、枚举出来所有的可以获得的关于解的信息,看看是否存在什么规律。这里推倒的方式往往是从边界开始往前推导,观察前后状态之间的联系。或者是从初始状态向后推导,找规律。
相关文章:

2022年蓝桥杯省赛软件类C/C++B组----积木画
想借着这一个题回顾一下动态规划问题的基本解法,让解题方法清晰有条理,希望更多的人可以更轻松的理解动态规划! 目录 【题目】 【本题解题思路】 【DP模版】 总体方针: 具体解题时的套路: 【题目】 【本题解题思…...

Python数据挖掘项目开发实战:使用朴素贝叶斯进行社会媒体挖掘
注意:本文下载的资源,与以下文章的思路有相同点,也有不同点,最终目标只是让读者从多维度去熟练掌握本知识点。 Python数据挖掘项目开发实战:使用朴素贝叶斯进行社会媒体挖掘 一、项目背景与目标 在社交媒体时代&…...

【DM8】ET SQL性能分析工具
通过统计SQL每个操作符的时间花费,从而定位到有性能问题的操作,指导用户去优化。 开启ET工具 INI参数: ENABLE_MONITOR1 MONITOR_SQL_EXEC1 查看参数 select * FROM v$dm_ini WHERE PARA_NAMEMONITOR_SQL_EXEC;SELECT * FROM v$dm_ini WH…...
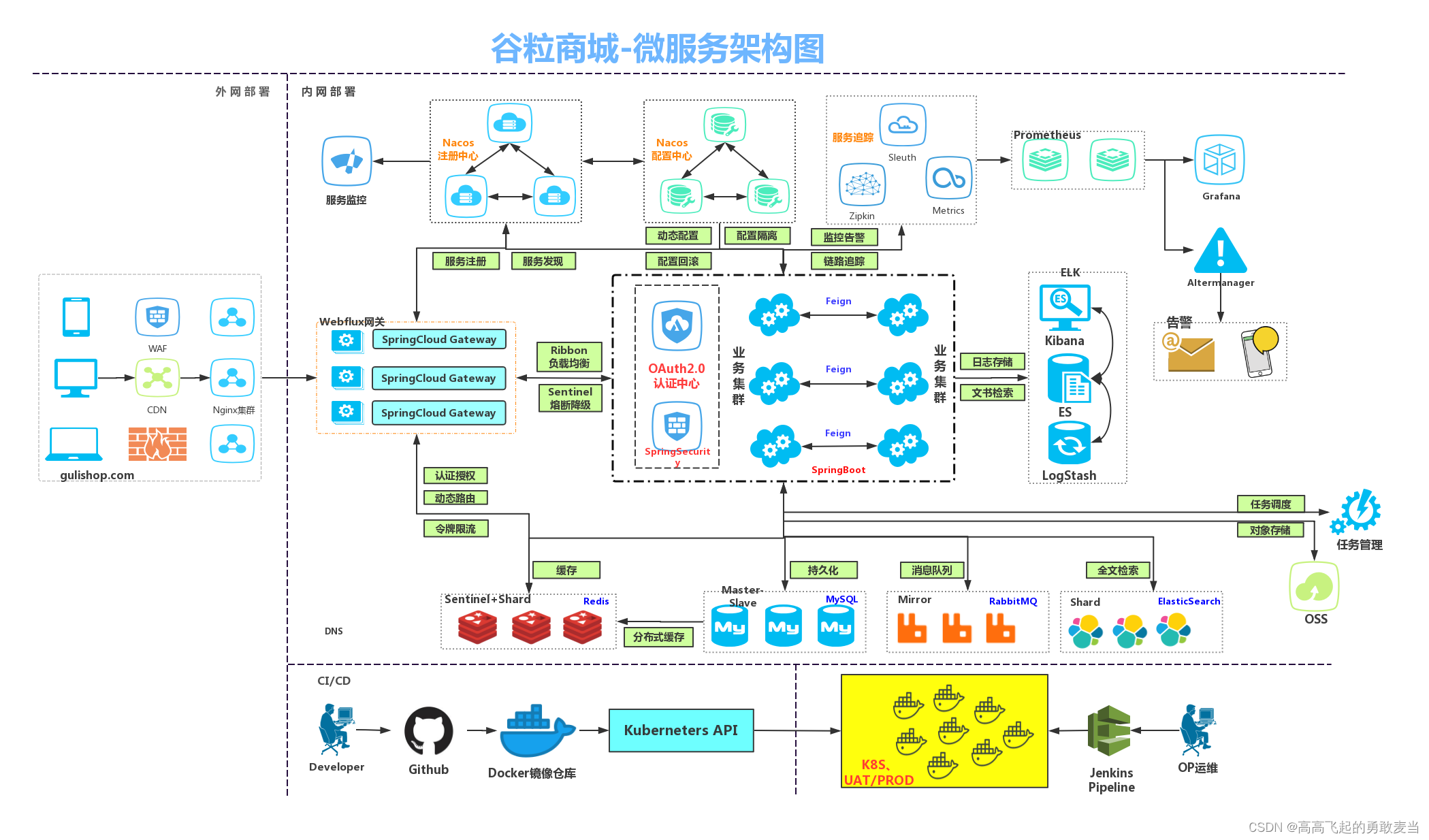
001-谷粒商城-微服务剖析
1、架构图 还是很强的,该有的都有 2、微服务模块 SpringCloudAlibaba组件包括 SentinelNacosRocketMQSeata 搭配SpringCloudAlibaba组件 OpenFeignGateWayRibbn gateway使用了SpringWebFlux,前几天研究到,为什么springboot不直接使用Spri…...
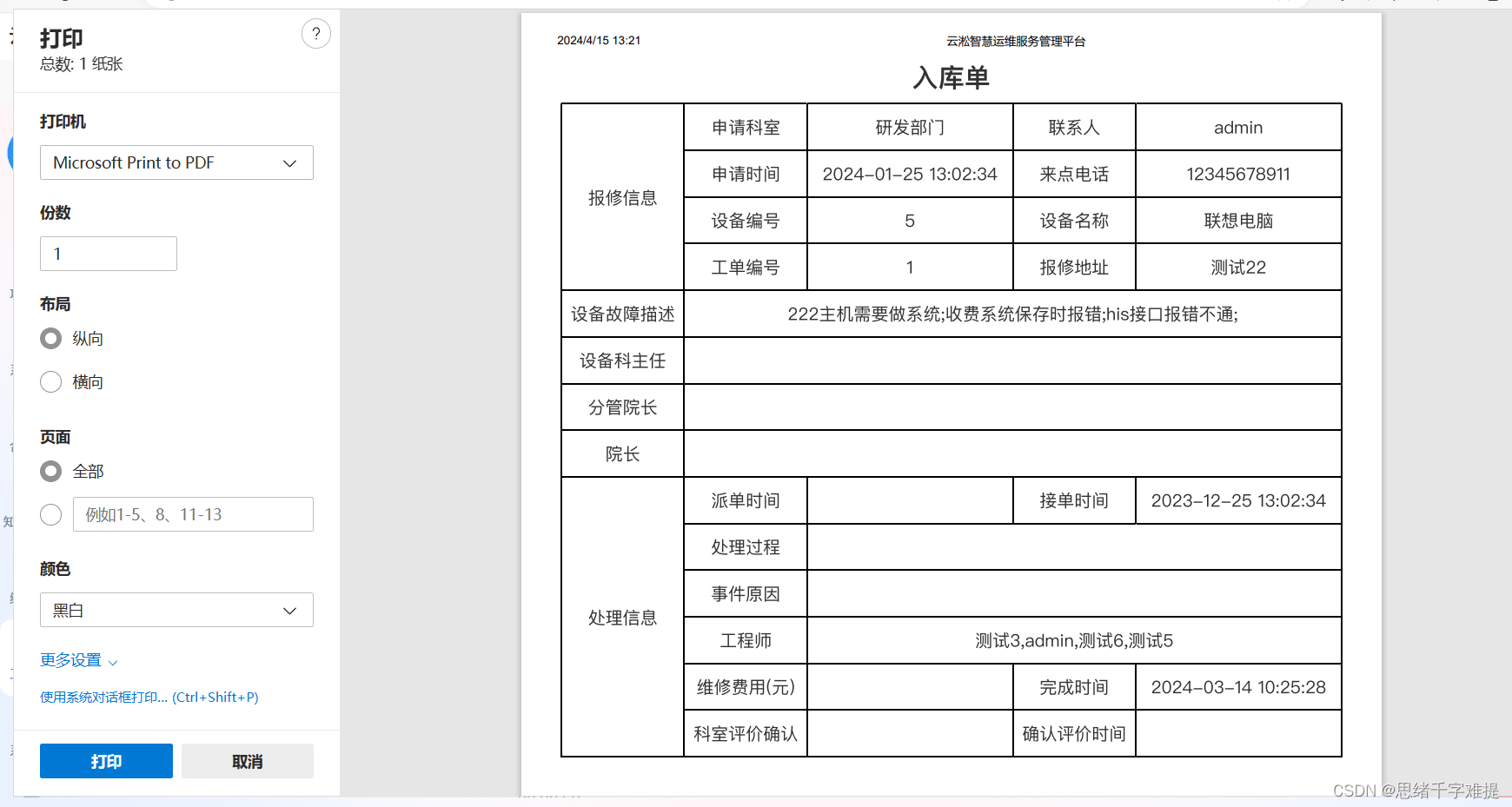
vue实现前端打印效果
如图效果所示(以下演示代码) <template><div><el-button v-print"printObj" type"primary" plain click"handle">{{ text }}</el-button><div style"display: none"><div id…...

android wifi直连 wifip2pmanager
android wifi直连 wifip2pmanager;使用WiFi 直连,然后通过udp进行通讯。 Android WiFi 直连(Wi-Fi Direct,也称为Wi-Fi P2P)是一种让两台或多台设备通过Wi-Fi技术直接进行点对点连接的技术,无需借助传统的无…...
伸缩应用程序和执行滚动更新
📕作者简介: 过去日记,致力于Java、GoLang,Rust等多种编程语言,热爱技术,喜欢游戏的博主。 📘相关专栏Rust初阶教程、go语言基础系列、spring教程等,大家有兴趣的可以看一看 📙Jav…...
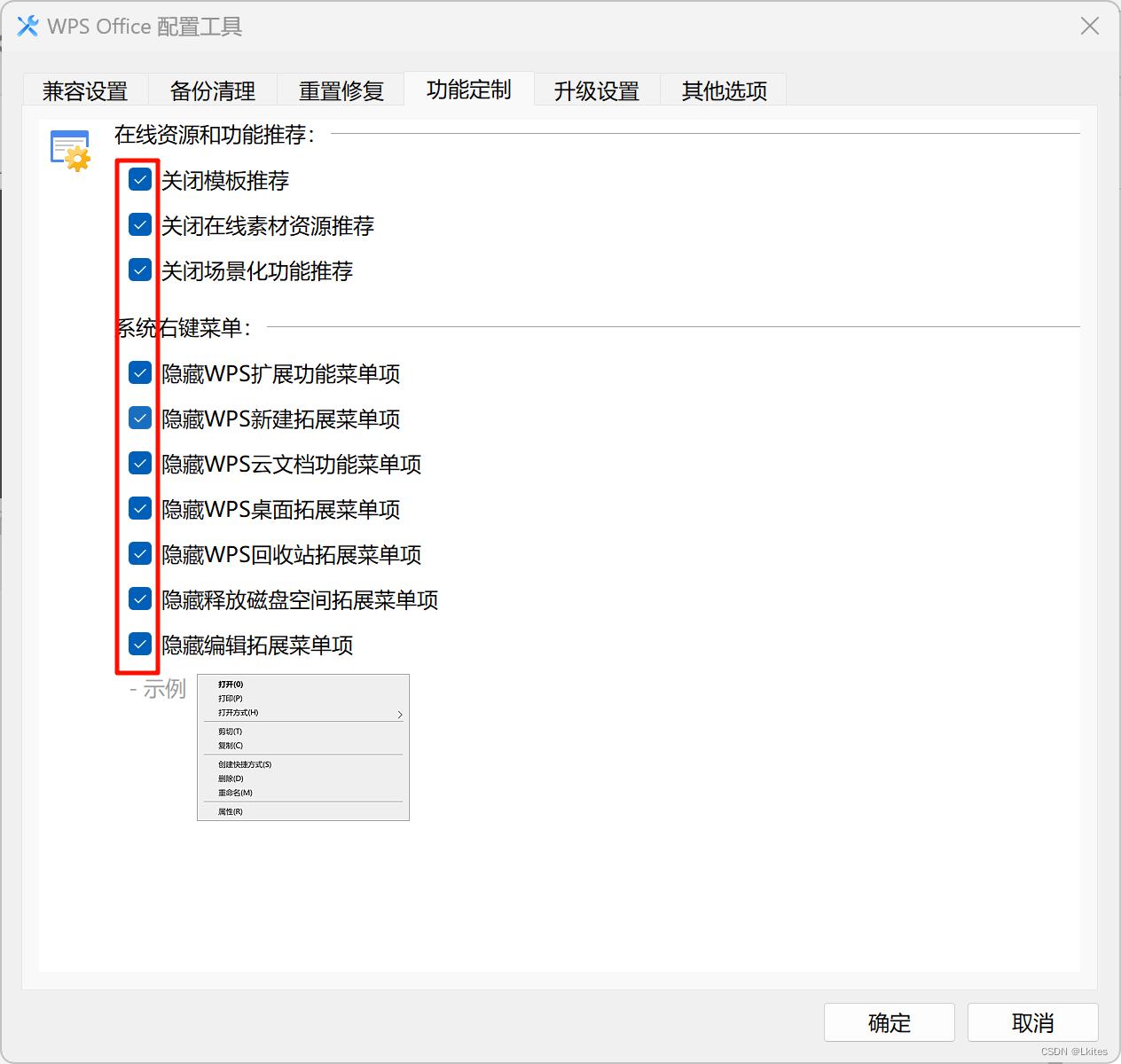
解决WPS右键菜单冗余选项,去除WPS右键菜单选项
问题描述 安装WPS后,右键菜单会多出许多无用的选项,如何去除? 解决方法 按下WindowsS打开搜索栏,搜索配置工具打开 勾选所有的关闭和隐藏选项...
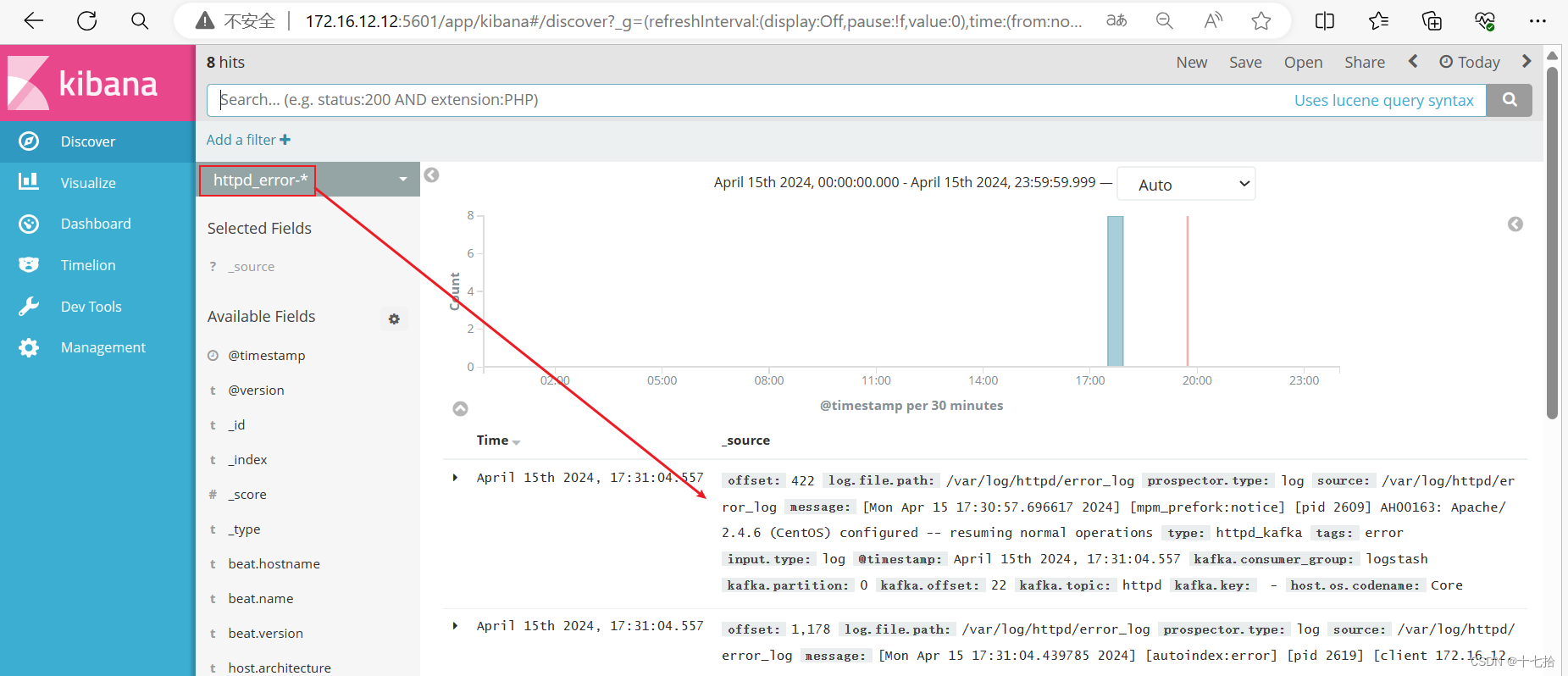
部署ELFK+zookeeper+kafka架构
目录 前言 一、环境部署 二、部署ELFK 1、ELFK ElasticSearch 集群部署 1.1 配置本地hosts文件 1.2 安装 elasticsearch-rpm 包并加载系统服务 1.3 修改 elasticsearch 主配置文件 1.4 创建数据存放路径并授权 1.5 启动elasticsearch是否成功开启 1.6 查看节点信息 …...

ActiveMQ 任意文件上传漏洞复现
一、使用弱口令登陆 访问 http://ip:8161/admin/ 进入admin登陆页面,使用弱口令登陆,账号密码皆为 admin,登陆成功后,headers中会出现验证信息 如: Authorization: Basic YWRtaW46YWRtaW4 # 二、利用PUT协议上…...

k8s实践总结
一、pod常用操作: 1、如何重启pod? 1.1 删除并重新创建Pod 这是最直接的方法。你可以通过kubectl命令行工具删除Pod,然后Kubernetes将基于其对应的Deployment、ReplicaSet或其他控制器自动重新创建它。 不建议并行删除全部pod,…...

前端从零到一搭建脚手架并发布到npm
这里写自定义目录标题 为什么需要脚手架?前置-第三方工具的使用1. 创建demo并运行-4步新建文件夹 zyfcli,并初始化npm init -y配置入口文件 2.commander-命令行指令3. chalk-命令行美化工具4. inquirer-命令行交互工具5. figlet-艺术字6. ora-loading工具…...

使用 git 提交项目到 github
文章推荐:https://zhuanlan.zhihu.com/p/193140870 连接失败:https://zhuanlan.zhihu.com/p/521340971 分支出错:https://blog.csdn.net/gongdamrgao/article/details/115032436...

SRE 与传统 IT 运营有何不同?
软件开发和部署方法的发展要求组织管理和维护 IT 基础设施的方式发生转变。站点可靠性工程(SRE) 是一门将软件工程的各个方面融入 IT 运营的学科,处于这一变革的前沿。随着专业人士和组织都寻求适应,对 SRE 认证和培训计划的需求激增。本博客探讨了 SRE …...
html公众号页面实现点击按钮跳转到导航
实现效果: 点击导航自动跳转到: html页面代码: <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><title>跳转导航</title><meta name"keywords" conten…...

【算法】快速排序的基本思想、优化 | 挖坑填补法和区间分割法
创作不易,本篇文章如果帮助到了你,还请点赞 关注支持一下♡>𖥦<)!! 主页专栏有更多知识,如有疑问欢迎大家指正讨论,共同进步! 更多算法分析与设计知识专栏:算法分析🔥 给大家跳…...

OSPF动态路由实验(华为)
思科设备参考:OSPF动态路由实验(思科) 一,技术简介 OSPF(Open Shortest Path First)是一种内部网关协议,主要用于在单一自治系统内决策路由。它是一种基于链路状态的路由协议,通过…...

EasyRecovery2024专业免费的电脑数据恢复软件
EasyRecovery数据恢复软件是一款功能强大的数据恢复工具,广泛应用于各种数据丢失场景,帮助用户从不同类型的存储介质中恢复丢失或删除的文件。 该软件支持恢复的数据类型非常广泛,包括但不限于办公文档、图片、音频、视频、电子邮件以及各种…...
Vue集成PageOffice实现在线编辑word、excel(前端配置)
一、什么是PageOffice PageOffice是一款在线的office编辑软件,帮助Web应用系统或Web网站实现用户在线编辑Word、Excel、PowerPoint文档。可以完美实现在线公文流转,领导批阅,盖章。可以给文件添加水印,在线安全预览防止用户下载…...

IBM SPSS Statistics for Mac:数据分析的卓越工具
IBM SPSS Statistics for Mac是一款功能强大的数据分析软件,专为Mac用户设计,提供了一系列专业的统计分析和数据管理功能。无论是科研人员、数据分析师还是学生,都能从中获得高效、准确的数据分析支持。 IBM SPSS Statistics for Mac v27.0.1…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...
