C语言——内存函数的实现和模拟实现
1. memcpy 使用和模拟实现
void * memcpy ( void * destination, const void * source, size_t num );
- 函数memcpy从source的位置开始向后复制num个字节的数据到destination指向的内存位置。
- 这个函数在遇到 '\0' 的时候并不会停下来。
- 如果source和destination有任何的重叠,复制的结果都是未定义的
#define _CRT_SECURE_NO_WARNINGS#include <stdio.h>
#include <string.h>
int main()
{int arr1[] = { 1,2,3,4,5,6,7,8,9,10 };int arr2[10] = { 0 };memcpy(arr2, arr1, 20);//int类型,一个为四个四节//将arr1里前20字节复制到arr2数组中int i = 0;for (i = 0; i < 10; i++){printf("%d ", arr2[i]);}return 0;
}对于重叠的部分,可以交给memmove处理;
memcpy函数的模拟实现:
void* memcpy(void* dst, const void* src, size_t count){void* ret = dst;assert(dst);assert(src);while (count--) { *(char*)dst = *(char*)src; //先是void函数未定义,在通过强类型转换,转换为char*(解引用后为一个字节)dst = (char*)dst + 1;src = (char*)src + 1;}return(ret);}2. memmove 使用和模拟实现
void * memmove ( void * destination, const void * source, size_t num );
- 和memcpy的差别就是memmove函数处理的源内存块和目标内存块是可以重叠的。
- 如果源空间和目标空间出现重叠,就得使用memmove函数处理。
#include <stdio.h>
#include <string.h>
int main()
{int arr1[] = { 1,2,3,4,5,6,7,8,9,10 };memmove(arr1 + 2, arr1, 20);int i = 0;for (i = 0; i < 10; i++){printf("%d ", arr1[i]);}return 0;
}输出结果:1 2 1 2 3 4 5 8 9 10
void * memmove ( void * dst, const void * src, size_t count)
{void * ret = dst;if (dst <= src || (char *)dst >= ((char *)src + count)) {while (count--) {*(char *)dst = *(char *)src;dst = (char *)dst + 1;src = (char *)src + 1;}}else {dst = (char *)dst + count - 1;src = (char *)src + count - 1;while (count--) {*(char *)dst = *(char *)src;dst = (char *)dst - 1;src = (char *)src - 1;}}return(ret);
}3. memset 函数的使用
void * memset ( void * ptr, int value, size_t num );
#include <stdio.h>
#include <string.h>
int main()
{char str[] = "hello world";memset(str, 'x', 6);printf(str);return 0;
}输出结果:xxxxxxworld
4.memcmp 函数的使用
int memcmp ( const void * ptr1, const void * ptr2, size_t num );
- 比较从ptr1和ptr2指针指向的位置开始,向后的num个字节
- 返回值如下:
#include <stdio.h>
#include <string.h>
int main()
{char buffer1[] = "DW2000000000";char buffer2[] = "DW1111111111";int n;n = memcmp(buffer1, buffer2, sizeof(buffer1));if (n > 0)printf("'%s' is greater than '%s'.\n", buffer1, buffer2);else if (n < 0)printf("'%s' is less than '%s'.\n", buffer1, buffer2);elseprintf("'%s' is the same as '%s'.\n", buffer1, buffer2);return 0;
}输出结果: 'DW2000000000' is greater than 'DW1111111111'.

相关文章:

C语言——内存函数的实现和模拟实现
1. memcpy 使用和模拟实现 void * memcpy ( void * destination, const void * source, size_t num ); 函数memcpy从source的位置开始向后复制num个字节的数据到destination指向的内存位置。 这个函数在遇到 \0 的时候并不会停下来。 如果source和destination有任何的重叠&am…...

如何优化邮箱Webhook API发送邮件的性能?
邮箱Webhook API发送邮件的流程?怎么用邮箱API发信? 高效、稳定的邮箱Webhook API发送邮件功能对于企业的日常运营至关重要。随着业务量的增长,如何优化邮箱Webhook API发送邮件的性能。AokSend将从多个方面探讨如何提升的效率。 邮箱Webho…...
)
OceanBase V4.X中常用的SQL(一)
整理了一些在OceanBase使用过程中常用的SQL语句,这些语句均适用于4.x版本,并将持续进行更新。后续还将分享一些V4.x版本常用的操作指南,以便更好地帮助大家使用OceanBase数据库。 集群信息 版本查看 show variables like version_comment; …...

代码随想录算法训练营第五十天|123.买卖股票的最佳时机III 188.买卖股票的最佳时机IV
123.买卖股票的最佳时机III 这道题一下子就难度上来了,关键在于至多买卖两次,这意味着可以买卖一次,可以买卖两次,也可以不买卖。 视频讲解:https://www.bilibili.com/video/BV1WG411K7AR https://programmercarl.com…...
)
Composer安装与配置:简化PHP依赖管理的利器(包括加速镜像设置)
在现代的PHP开发中,我们经常会使用许多第三方库和工具来构建强大的应用程序。然而,手动管理这些依赖项可能会变得复杂和耗时。为了解决这个问题,Composer应运而生。Composer是一个PHP的依赖管理工具,它可以帮助我们轻松地安装、更…...

灯塔:抽象类和接口笔记
什么是构造方法 构造方法是一种特殊的方法,它是一个与类同名且没有返回值类型的方法。 构造方法的功能主要是完成对象的初始化。当类实例化一个对象时会自动调用构造方法,且构造方法和其他方法一样也可以重载 继承抽象类需要实现所有的抽象方法吗 继…...

mybatis 入门
MyBatis是一款持久层框架,免除了几乎所有的JDBC代码、参数及获取结果集工作。可以通过简单的XML或注解来配置和映射原始类型、接口和Java POJO为数据库中的记录。 1 无框架下的JDBC操作 1)加载驱动:Class.forName(“com.mysql.cj.jdbc.Driv…...

Spring-AI-上下文记忆
引入依赖 pom文件 <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http://www.w3.org/2001/XMLSchema-instance"xsi:schemaLocation"http://maven.apache.org/P…...

内存函数memcpy、mommove、memset、memcmp
目录 1、memcpy函数 memcpy函数的模拟实现 2、memmove函数 memmove函数的模拟实现 3、memset函数 4、memcmp函数 1、memcpy函数 描述: C 库函数 void *memcpy(void *str1, const void *str2, size_t n) 从存储区 str2 复制 n 个字节到存储区 str1。 声明&…...

symfony框架介绍
Symfony是一个功能强大的PHP框架,它提供了丰富的组件和工具来简化Web开发过程。以下是一些关于Symfony的主要特点: 可重用性: Symfony提供了一系列可重用的PHP组件,这些组件可以用于任何PHP应用程序中。灵活性: Symfony允许开发者根据项目需求灵活选择使用哪些组件,而不是强…...
【计算机毕业设计】游戏售卖网站——后附源码
🎉**欢迎来到琛哥的技术世界!**🎉 📘 博主小档案: 琛哥,一名来自世界500强的资深程序猿,毕业于国内知名985高校。 🔧 技术专长: 琛哥在深度学习任务中展现出卓越的能力&a…...
LabVIEW电信号傅里叶分解合成实验
LabVIEW电信号傅里叶分解合成实验 电信号的分析与处理在科研和工业领域中起着越来越重要的作用。系统以LabVIEW软件为基础,开发了一个集电信号的傅里叶分解、合成、频率响应及频谱分析功能于一体的虚拟仿真实验系统。系统不仅能够模拟实际电路实验箱的全部功能&…...

Docker 学习笔记(六):挑战容器数据卷技术一文通,实战多个 MySQL 数据同步,能懂会用,初学必备
一、前言 记录时间 [2024-4-11] 系列文章简摘: Docker学习笔记(二):在Linux中部署Docker(Centos7下安装docker、环境配置,以及镜像简单使用) Docker 学习笔记(三)&#x…...

csdn怎么变得这么恶心,自动把一些好的文章分享改成了vip可见
刚刚发现以前发的一些文章未经过我同意,被csdn自动改成了VIP可见,这也太恶心了,第一你没分钱给我,第二我记录下一些问题也不是为了赚钱,而是为了提升自己和帮助别人,这样搞是想逼更多人走是吗?...

自然语言处理NLP:文本预处理Text Pre-Processing
大家好,自然语言处理(NLP)是计算机科学领域与人工智能领域中的一个重要方向,其研究能实现人与计算机之间用自然语言进行有效通信的各种理论和方法。本文将介绍文本预处理的本质、原理、应用等内容,助力自然语言处理和模型的生成使用。 1.文本…...
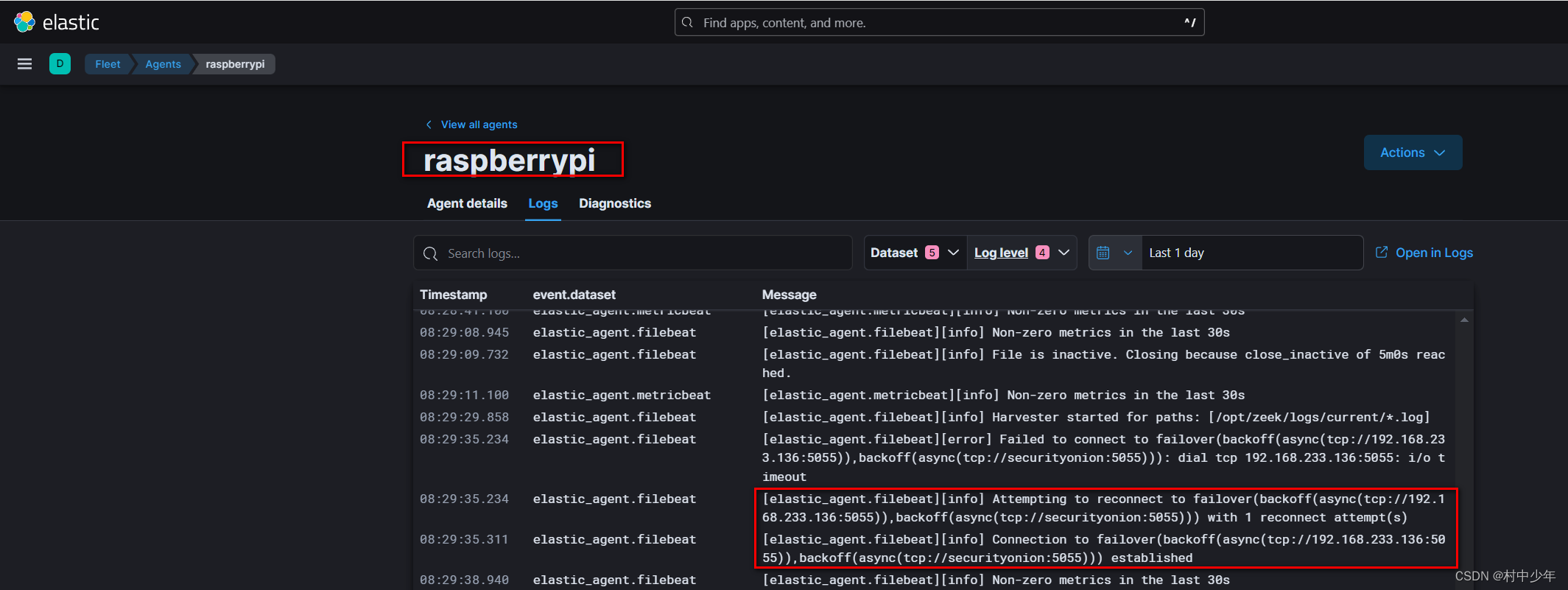
家庭网络防御系统搭建-虚拟机安装siem/securityonion网络连接问题汇总
由于我是在虚拟机中安装的security onion,在此过程中,遇到很多的网络访问不通的问题,通过该文章把网络连接问题做一下梳理。如果直接把securityonion 安装在物理机上,网络问题则会少很多。 NAT无法访问虚拟机 security onion虚拟…...
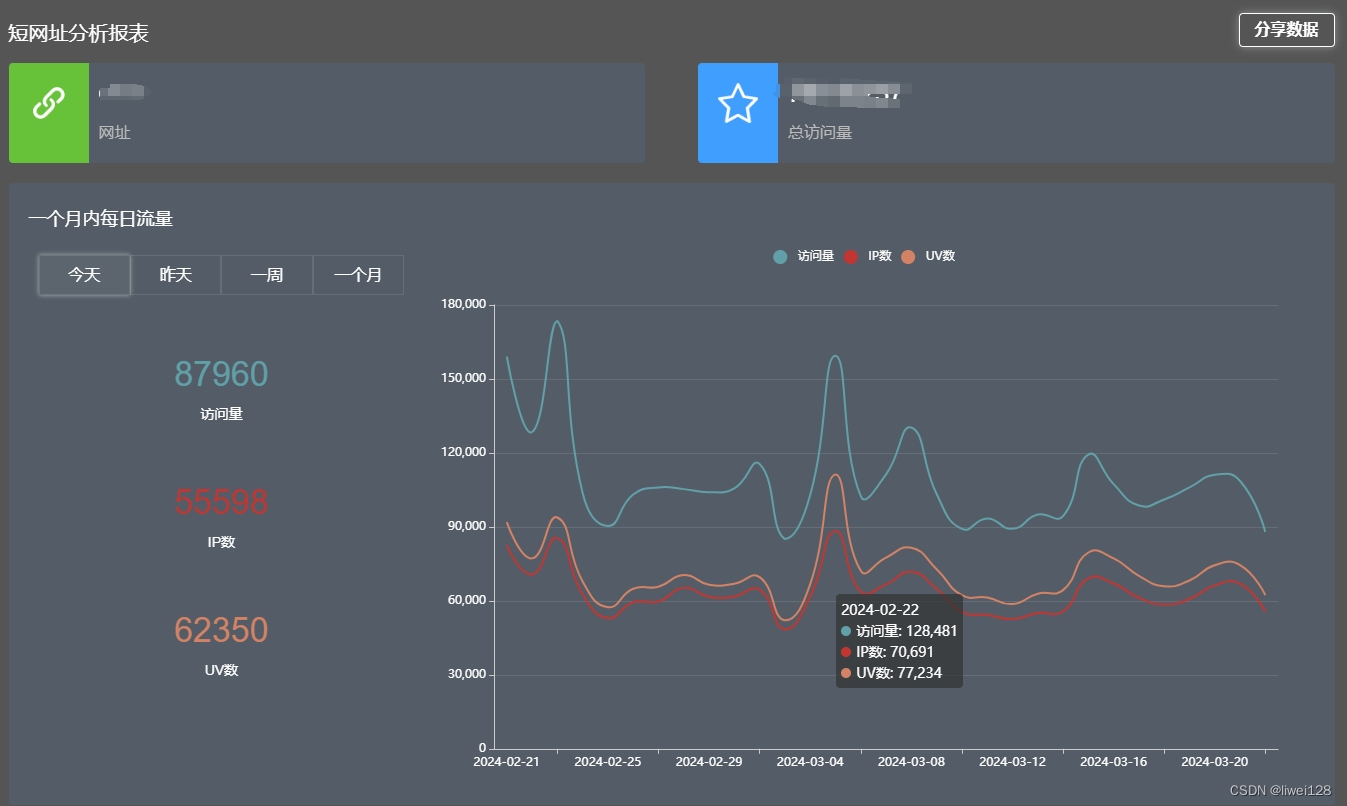
2024年外贸行业营销神器推荐
2024年外贸行业营销神器推荐:外贸人每天面对的不是国内客户,而是全球客户,相对于国内来说,会更加麻烦和繁琐,今天就码一篇2024年外贸行业营销神器的推荐文章,希望可以减轻各位外贸人的负担! 1、…...

k8s高可用集群部署介绍 -- 理论
部署官网参考文档 负载均衡参考 官网两种部署模式拓扑图和介绍 介绍两种高可用模式 堆叠 拓扑图如下(图片来自k8s官网): 特点:将etcd数据库作为控制平台的一员,由于etcd的共识算法,所以集群最少为3个&…...

【GDAL-Python】1-在Python中使用GDAL读写栅格文件
文章目录 1-概要2.代码实现 1-概要 提示:本教程介绍如何使用 Python 中的 GDAL 库将栅格数据读取为数组并将数组另存为GeoTiff 文件 视频地址:B站对应教程 目标: (1)读写GeoTiff影像; (2&…...

【C++】explicit关键字详解(explicit关键字是什么? 为什么需要explicit关键字? 如何使用explicit 关键字)
目录 一、前言 二、explicit关键字是什么? 三、构造函数还具有类型转换的作用 🍎单参构造函数 ✨引出 explicit 关键字 🍍多参构造函数 ✨为什么需要explicit关键字? ✨怎么使用explicit关键字? 四、总结 五…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

【Nginx】使用 Nginx+Lua 实现基于 IP 的访问频率限制
使用 NginxLua 实现基于 IP 的访问频率限制 在高并发场景下,限制某个 IP 的访问频率是非常重要的,可以有效防止恶意攻击或错误配置导致的服务宕机。以下是一个详细的实现方案,使用 Nginx 和 Lua 脚本结合 Redis 来实现基于 IP 的访问频率限制…...

SQL Server 触发器调用存储过程实现发送 HTTP 请求
文章目录 需求分析解决第 1 步:前置条件,启用 OLE 自动化方式 1:使用 SQL 实现启用 OLE 自动化方式 2:Sql Server 2005启动OLE自动化方式 3:Sql Server 2008启动OLE自动化第 2 步:创建存储过程第 3 步:创建触发器扩展 - 如何调试?第 1 步:登录 SQL Server 2008第 2 步…...

用鸿蒙HarmonyOS5实现中国象棋小游戏的过程
下面是一个基于鸿蒙OS (HarmonyOS) 的中国象棋小游戏的实现代码。这个实现使用Java语言和鸿蒙的Ability框架。 1. 项目结构 /src/main/java/com/example/chinesechess/├── MainAbilitySlice.java // 主界面逻辑├── ChessView.java // 游戏视图和逻辑├──…...
