LeetCode 1702.修改后的最大二进制字符串:脑筋急转弯(构造,贪心)
【LetMeFly】1702.修改后的最大二进制字符串:脑筋急转弯(构造,贪心)
力扣题目链接:https://leetcode.cn/problems/maximum-binary-string-after-change/
给你一个二进制字符串 binary ,它仅有 0 或者 1 组成。你可以使用下面的操作任意次对它进行修改:
- 操作 1 :如果二进制串包含子字符串
"00",你可以用"10"将其替换。<ul><li>比方说, <code>"<strong>00</strong>010" -> "<strong>10</strong>010"</code></li> </ul> </li> <li>操作 2 :如果二进制串包含子字符串 <code>"10"</code> ,你可以用 <code>"01"</code> 将其替换。 <ul><li>比方说, <code>"000<strong>10</strong>" -> "000<strong>01</strong>"</code></li> </ul> </li>
请你返回执行上述操作任意次以后能得到的 最大二进制字符串 。如果二进制字符串 x 对应的十进制数字大于二进制字符串 y 对应的十进制数字,那么我们称二进制字符串 x 大于二进制字符串 y 。
示例 1:
输入:binary = "000110" 输出:"111011" 解释:一个可行的转换为: "000110" -> "000101" "000101" -> "100101" "100101" -> "110101" "110101" -> "110011" "110011" -> "111011"
示例 2:
输入:binary = "01" 输出:"01" 解释:"01" 没办法进行任何转换。
提示:
1 <= binary.length <= 105binary仅包含'0'和'1'。
解题方法:构造(贪心)
题目分析
如果给定字符串中没有0,则不在本次讨论的范围之列,直接返回原字符串。
推论1:最终字符串中一定有0
仅有的两种变换分别是00->10和10->01,只能减少0的个数,但永远不可能将所有0消除。
推论2:最终字符串中一定只有一个0
以10111011为例,该字符串中有两个0,则可以进行以下变换10111011->10011111->11011111,具体变换过程如下:
10111011
10110111 ---+
10101111 +---后面的那个0不断地通过10->01的变换最终和前面那个0相邻
10011111 ---+
11011111 -> 相邻两个0通过00->10的变换使得二进制字符串相比于初始值更大了
也就是说,假设最终字符串中有两个0,那么后面的那个0一定可以通过10->01的变换与前面的0相邻,相邻两个0再通过00->10变换,使得第一个0变成了1,字符串值更大了。
若有多个0则同理,最终一定只剩下一个0,变成111..11011..111的形态。
为什么不继续变化了呢?因为11、01都不可变,唯一可变的是10->01。但是这么变的话相当于“0往前移”了,字符串值更小,不可取。
如何判断最终字符串中0的位置?
由给定的两种变换00->10和10->01可以发现,0要么被消除(变换一)要么左移(变换二),单纯的左移会导致字符串变小,因此尽量将最前面的0“消除”。
如何消除?通过变换一消除。通过推论2我们知道,只要存在两个0,则右边的0必定能千里迢迢地来到左边的0身边并与之进行变换一:
111..11011..11011..11
111..11001..11111..11
111..11101..11111..11
也就是说,第一个0的右边每存在一个0,就能让第一个0的位置“右移一位”。
最终第一个0(也就是唯一的一个0)的位置,是原始字符串中第一个0的位置,再右移 0 的总个数 − 1 0的总个数 - 1 0的总个数−1位。
具体方法
给定字符串,统计其中0的个数(记为cnt0)。
若无0,则直接返回原始字符串;否则继续。
找到字符串中第一个0的位置(记为pos0),构造一个只有pos0 + cnt0 - 1这个位置为0其余位置全部为1的字符串并返回。
时空复杂度分析
- 时间复杂度 O ( l e n ( b i n a r y ) ) O(len(binary)) O(len(binary))
- 空间复杂度 O ( l e n ( b i n a r y ) ) O(len(binary)) O(len(binary)):空间复杂度来自字符串构造过程中的临时变量。
AC代码
C++
class Solution {
public:string maximumBinaryString(string binary) {int cnt0 = count(binary.begin(), binary.end(), '0');if (!cnt0) {return binary;}int first0 = binary.find('0');return string(first0 + (cnt0 - 1), '1') + '0' + string(binary.size() - (first0 + (cnt0 - 1)) - 1, '1');}
};
Python
class Solution:def maximumBinaryString(self, binary: str) -> str:cnt0 = binary.count('0')if not cnt0:return binaryfirst0 = binary.find('0')pos0 = first0 + (cnt0 - 1)return '1' * pos0 + '0' + '1' * (len(binary) - pos0 - 1)
同步发文于CSDN和我的个人博客,原创不易,转载经作者同意后请附上原文链接哦~
Tisfy:https://letmefly.blog.csdn.net/article/details/137593422
相关文章:
)
LeetCode 1702.修改后的最大二进制字符串:脑筋急转弯(构造,贪心)
【LetMeFly】1702.修改后的最大二进制字符串:脑筋急转弯(构造,贪心) 力扣题目链接:https://leetcode.cn/problems/maximum-binary-string-after-change/ 给你一个二进制字符串 binary ,它仅有 0 或者 1 组…...
图片像素轻松缩放自如,支持批量将多张jpg图片像素放大,高效掌握图片的像素
在这个数字化时代,图片已经成为我们生活中不可或缺的一部分。然而,你是否曾遇到过需要放大图片像素却担心失去细节和质量的问题?现在,一款全新的图片缩放工具诞生了,它能够让你轻松将多张JPG图片像素放大,同…...
FILE类与IO流
目录 File类的实例化与常用方法 File类的理解 文件路径的表示方式: API的使用 IO流概述与流的分类 I/O流中的是Input/Output的缩写 IO流的分类(不同角度) Java程序中的IO流涉及40多个,但实际上都是由4个抽象类衍生出来的。 F…...
基于java+springboot+vue实现的智慧党建系统(文末源码+Lw+ppt)23-58
摘 要 当今社会进入了科技进步、经济社会快速发展的新时代。国际信息和学术交流也不断加强,计算机技术对经济社会发展和人民生活改善的影响也日益突出,人类的生存和思考方式也产生了变化。传统智慧党建管理采取了人工的管理方法,但这种管…...

HiveSQL基础Day03
回顾总结 hive表的类型 :内部表和外部表 删除内部表会删除表的所有数据 删除外部表只会删除表的元数据,hdfs上的行数据会保留 表的分区和分桶 本质都是对表数据的拆分存储 分区的方式 是通过创建不同的目录来拆分数据 ,根据数据本身的内容最为…...

houdini 学习过程
1.基础界面操作了解 当初通过 朱峰上的界面 工具栏操作入门的,现在B站上应该也比较多 houdini pdf早期的 2.节点操作 B站视频 教程 3.vex B站捷佳 4.BILIBILI ENTAGMA CGWIKI YOUTUBE 5.节点功能的深入,属性了解,或其它节点扩充 常用&…...
Angular学习第四天--问题记录及父子组件问题
问题一、 拉取完项目,使用npm install命令的时候遇到的。 解决办法: 在查找网上五花八门的解决方案之后,发现都不能解决。 我的解决办法是: 1. 把package-lock.json给删掉; 2. 把package.json中公司自己库的包给删除掉…...
如何拿捏2024年的B端设计?(附工具推荐)
伴随着2019年前的互联网人口红利时代结束,科技行业的基本面发生了巨大的变化,以普通消费者为目标的C端需求大幅萎缩,面向企业的B端需求成为行业热点。 在2024年的今天,设计师应该如何理解B端设计的实质,并真正驾驭B端产…...

【蓝桥杯】2024年第15届真题题目
试题 A: 握手问题 本题总分: 5 分 【问题描述】 小蓝组织了一场算法交流会议,总共有 50 人参加了本次会议。在会议上, 大家进行了握手交流。按照惯例他们每个人都要与除自己以外的其他所有人进 行一次握手(且仅有一次&a…...
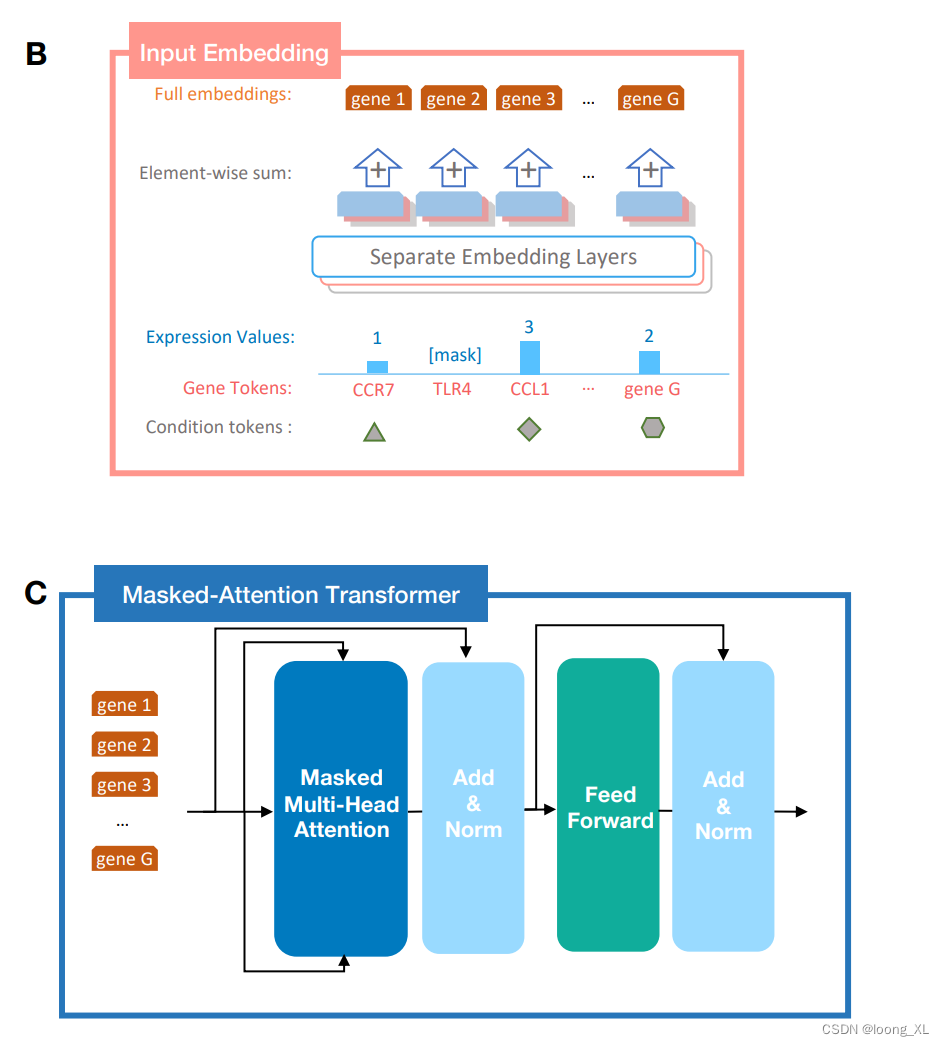
LLM生成模型在生物单细胞single cell的应用:scGPT
参考: https://github.com/bowang-lab/scGPT https://www.youtube.com/watch?vXhwYlgEeQAs 相关算法: 主要是把单细胞测序出来的基因表达量的拼接起来构建成的序列,这里不是用的基因的ATCG,是直接用的基因名称 训练数据&#x…...

力扣15题. 三数之和
题目: 给你一个整数数组 nums ,判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i ! j、i ! k 且 j ! k ,同时还满足 nums[i] nums[j] nums[k] 0 。请 你返回所有和为 0 且不重复的三元组。 注意:答案中不可以包含重复…...

项目经理好还是产品经理好?入行必读!
在现代项目管理领域,产品经理Product Manager和项目经理Project Manager,两者虽都是PM,但两者在实际操作中却有着显著的区别,在各自的领域中承担着不同的岗位职责和工作。 项目经理跟产品经理两个证都挺受市场欢迎的,…...
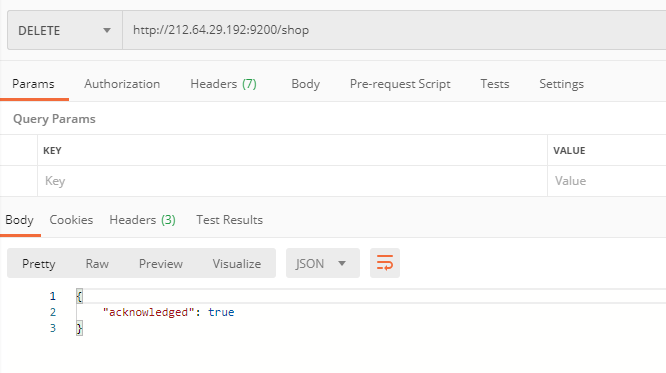
Elastic安装后 postman对elasticsearch进行测试
一、创建索引和mapping //id 字段自增id //good_sn 商品SKU //good_name 商品名称 //good_introduction 商品简介 //good_descript 商品详情 PUT http://IP:9200/shop { "mappings":{ "good":{ "properties":{ …...

JPA (Java Persistence API)
一、Jpa的介绍 JPA ,是一套Sun公司Java官方制定的ORM 规范。 ORM,即 对象关系映射 (Object Relational Mapping),是一种程序技术,用于 在关系数据库和业务实体对象之间做映射 。ORM 框架的存在,…...

实战要求下,如何做好资产安全信息管理
文章目录 一、资产安全信息管理的重要性二、资产安全信息管理的痛点三、如何做好资产安全信息管理1、提升资产安全信息自动化、集约化管理能力,做到资产全过程管理2、做好资产的安全风险识别3、做好互联网暴露面的测绘与管空4、做好资产安全信息的动态稽核管理 “摸…...
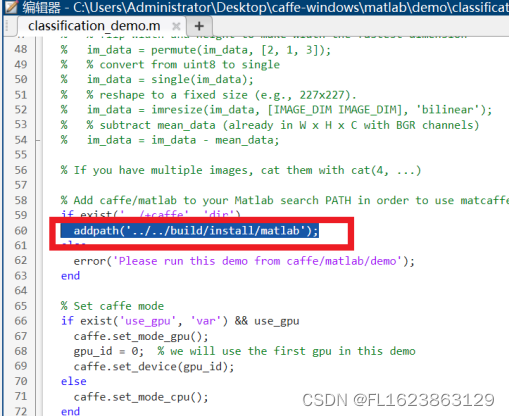
[matlab]matcaffe在matlab2023a安装和配置过程
测试环境: caffe-windows-cpu-py35-matlab2018b-vs2015-20220321 matlab2023a 注意:由于matlab新版本不允许添加特殊目录,比如有和private目录,添加后也会警告,但是可以忽略。因此可以使用我研发的matlab环境添加工具…...

【word2pdf】Springboot word转pdf(自学使用)
文章目录 概要整体介绍具体实现官网pom文件增加依赖 遇到的问题本地运行OK,发布到Linux报错还是本地OK,但是Linux能运行的,但是中文乱码 小结 概要 Springboot word 转 pdf 整体介绍 搜了一下,发现了能实现功能的方法有四种 U…...
3_2Linux中内核级加强型火墙的管理
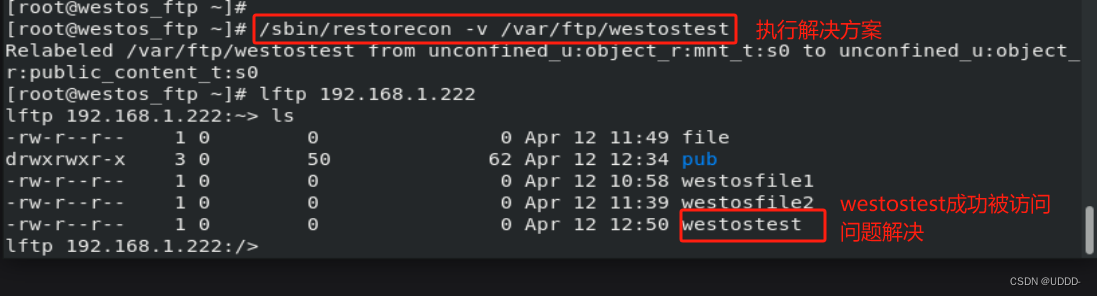
### 一.Selinux的功能 ### 观察现象 ①当Selinux未开启时 在/mnt中建立文件被移动到/var/ftp下可以被vsftpd服务访问 匿名用户可以通过设置后上传文件 当使用ls -Z /var/ftp查看文件时显示"?" ps auxZ | grep vsftpd 时显示: - root 8546 0.0 0.0 26952 …...

PCB工艺规范及PCB设计安规原则
一、目的 规范产品的PCB工艺设计,规定PCB工艺设计的相关参数,使得PCB的设计满足可生产性、可测试性、安规、EMC、EMI等的技术规范要求,在产品设计过程中构建产品的工艺、技术、质量、成本优势。 二、适用范围 本规范适用于所有电了产品的PCB工…...
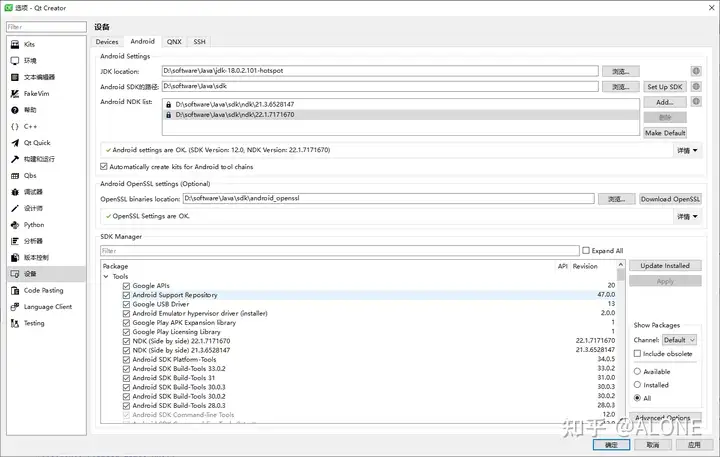
Qt for Android 开发环境
在搭建环境时开始感觉还挺顺利的,从 Qt 配置的环境里面看并没有什么问题,可真正编译程序的时候发现全是错误。 最开始的时候安装了 JDK21 最新版本,然后根据 JDK21 安装 ndk, build-tools, Platform-Tools 和 Gradle,但是不管这么…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】,分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...

关于uniapp展示PDF的解决方案
在 UniApp 的 H5 环境中使用 pdf-vue3 组件可以实现完整的 PDF 预览功能。以下是详细实现步骤和注意事项: 一、安装依赖 安装 pdf-vue3 和 PDF.js 核心库: npm install pdf-vue3 pdfjs-dist二、基本使用示例 <template><view class"con…...

android RelativeLayout布局
<?xml version"1.0" encoding"utf-8"?> <RelativeLayout xmlns:android"http://schemas.android.com/apk/res/android"android:layout_width"match_parent"android:layout_height"match_parent"android:gravity&…...

前端中slice和splic的区别
1. slice slice 用于从数组中提取一部分元素,返回一个新的数组。 特点: 不修改原数组:slice 不会改变原数组,而是返回一个新的数组。提取数组的部分:slice 会根据指定的开始索引和结束索引提取数组的一部分。不包含…...
