数据结构初阶:二叉树(一)
树概念及结构
树的概念

注意:树形结构中,子树之间不能有交集,否则就不是树形结构
 树的相关概念
树的相关概念

节点的度:一个节点含有的子树的个数称为该节点的度; 如上图:A的为6
叶节点或终端节点:度为0的节点称为叶节点; 如上图:B、C、H、I...等节点为叶节点
树的表示
typedef int DataType ;struct Node{struct Node * _firstChild1 ; // 第一个孩子结点struct Node * _pNextBrother ; // 指向其下一个兄弟结点DataType _data ; // 结点中的数据域};
 树在实际中的运用(表示文件系统的目录树结构)
树在实际中的运用(表示文件系统的目录树结构)
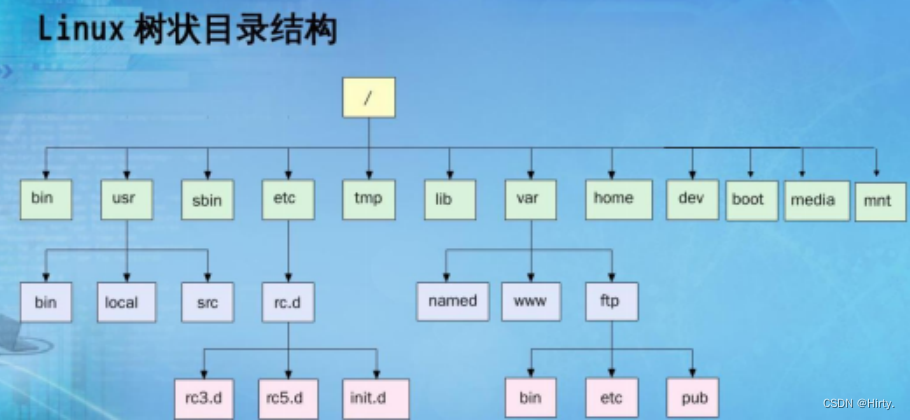
二叉树概念及结构
概念

从上图可以看出:

现实中的二叉树:

特殊的二叉树:

二叉树的性质


性质练习题:
1. 某二叉树共有 399 个结点,其中有 199 个度为 2 的结点,则该二叉树中的叶子结点数为( )A 不存在这样的二叉树B 200C 198D 1992. 下列数据结构中,不适合采用顺序存储结构的是( )A 非完全二叉树B 堆C 队列D 栈3. 在具有 2n 个结点的完全二叉树中,叶子结点个数为( )A nB n+1C n-1D n/24. 一棵完全二叉树的节点数位为 531 个,那么这棵树的高度为( )A 11B 10C 8D 125. 一个具有 767 个节点的完全二叉树,其叶子节点个数为()A 383B 384C 385D 386答案:1.B2.A3.A4.B5.B
二叉树的存储结构




typedef int BTDataType ;// 二叉链struct BinaryTreeNode{struct BinTreeNode * _pLeft ; // 指向当前节点左孩子struct BinTreeNode * _pRight ; // 指向当前节点右孩子BTDataType _data ; // 当前节点值域}// 三叉链struct BinaryTreeNode{struct BinTreeNode * _pParent ; // 指向当前节点的双亲struct BinTreeNode * _pLeft ; // 指向当前节点左孩子struct BinTreeNode * _pRight ; // 指向当前节点右孩子BTDataType _data ; // 当前节点值域} ;
二叉树的顺序结构及实现
二叉树的顺序结构
堆的概念及结构
堆的实现
堆向下调整算法
int array [] = { 27 , 15 , 19 , 18 , 28 , 34 , 65 , 49 , 25 , 37 };

堆的创建

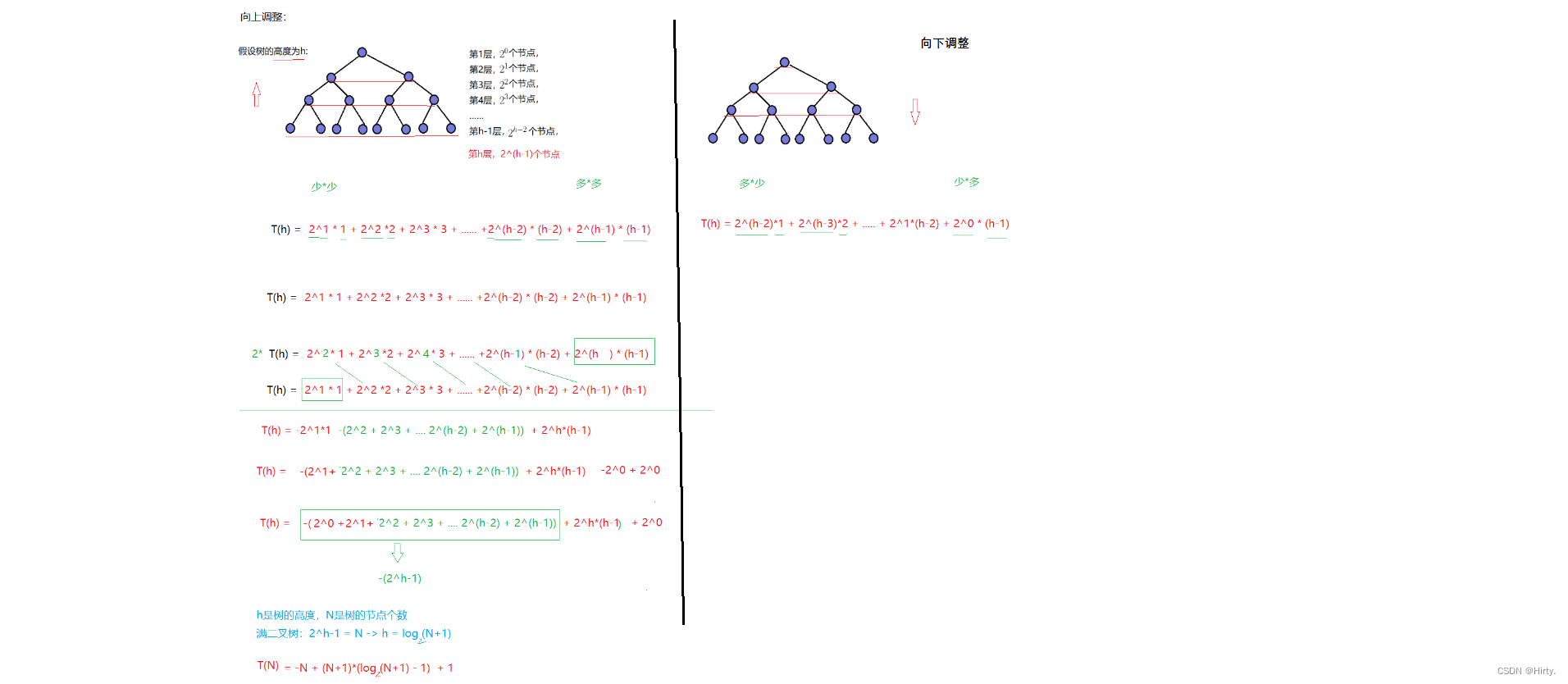
建堆时间复杂度
向下调整建堆的时间复杂度:O(N)

因此:建堆的时间复杂度为O(N)。故实际中我们选用向下调整建堆
向上调整建堆的时间复杂度:O(N*logN)
简单理解:
// O(N*logN)
for (int i = 0; i < n; i++) //插入N个数据,每个数据挪动logN次(因为h=log(N+1)),合计N*logN
{AdjustUp(a, i); //logN
}其实光看最后一层(占了一半的结点)就知道N/2个数据挪动logN次,即时间复杂度:O(N*logN)
堆的插入

堆的删除
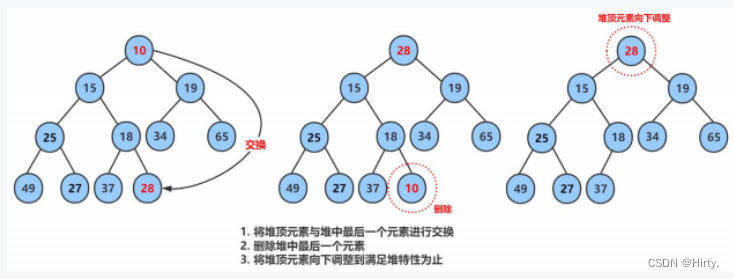
堆的代码实现(小堆)
Heap.h
#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>typedef int HPDataType;typedef struct Heap
{HPDataType* a;int size;int capacity;
}HP;void HeapInit(HP* php);
void HeapDestroy(HP* php);
void HeapPush(HP* php, HPDataType x);
// 规定删除堆顶(根节点)
void HeapPop(HP* php);
HPDataType HeapTop(HP* php);
int HeapSize(HP* php);
bool HeapEmpty(HP* php);void Swap(HPDataType* p1, HPDataType* p2);
void AdjustUp(HPDataType* a, int child);
void AdjustDown(HPDataType* a, int size, int parent);Heap.c
#include"Heap.h"// 小堆
void HeapInit(HP* php)
{assert(php);php->a = NULL;php->size = 0;php->capacity = 0;
}void HeapDestroy(HP* php)
{assert(php);free(php->a);php->a = NULL;php->size = php->capacity = 0;
}void Swap(HPDataType* p1, HPDataType* p2)
{HPDataType tmp = *p1;*p1 = *p2;*p2 = tmp;
}void AdjustUp(HPDataType* a, int child)
{int parent = (child - 1) / 2;while (child > 0){if (a[child] < a[parent]){Swap(&a[child], &a[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}
}// O(logN)
void HeapPush(HP* php, HPDataType x)
{assert(php);if (php->size == php->capacity){int newCapacity = php->capacity == 0 ? 4 : php->capacity * 2;HPDataType* tmp = (HPDataType*)realloc(php->a, newCapacity * sizeof(HPDataType));if (tmp == NULL){perror("realloc fail");exit(-1);}php->a = tmp;php->capacity = newCapacity;}php->a[php->size] = x;php->size++;AdjustUp(php->a, php->size - 1);
}void AdjustDown(int* a, int size, int parent)
{int child = parent * 2 + 1;while (child < size){// 假设左孩子小,如果解设错了,更新一下// child+1 < size 即没有右孩子,左孩子是最后一个if (child+1 < size && a[child + 1] < a[child]){++child;}if (a[child] < a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}void HeapPop(HP* php)
{assert(php);assert(php->size > 0);Swap(&php->a[0], &php->a[php->size - 1]);php->size--;AdjustDown(php->a, php->size, 0);
}HPDataType HeapTop(HP* php)
{assert(php);assert(php->size > 0);return php->a[0];
}int HeapSize(HP* php)
{assert(php);return php->size;
}bool HeapEmpty(HP* php)
{assert(php);return php->size == 0;
}
Test.c
#include"Heap.h"int main()
{int a[] = { 4,6,2,1,5,8,2,9};HP hp;HeapInit(&hp);for (int i = 0; i < sizeof(a) / sizeof(int); ++i){HeapPush(&hp, a[i]);}/*int k = 3;while (k--){printf("%d\n", HeapTop(&hp));HeapPop(&hp);}*/while (!HeapEmpty(&hp)){printf("%d ", HeapTop(&hp));HeapPop(&hp);}printf("\n");return 0;
}堆的应用
堆排序(选择排序)
堆排序即利用堆的思想来进行排序,总共分为两个步骤:
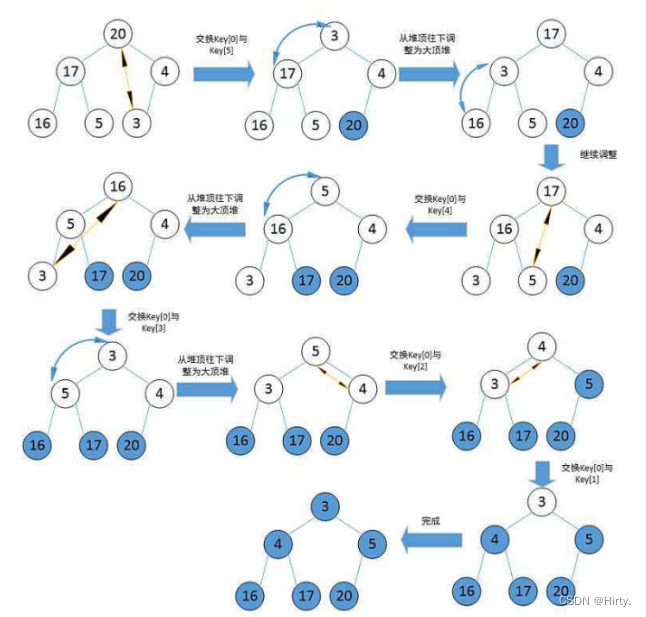
代码:

// 升序:建大堆
void HeapSort(int* a, int n)
{// 建大堆// O(N*logN)/*for (int i = 0; i < n; i++){AdjustUp(a, i);}*/// O(N)for (int i = (n-1-1)/2; i >= 0; --i){AdjustDown(a, n, i);}//O(N*logN),每次都从根节点开始向下调整高度次int end = n - 1;while (end > 0) {Swap(&a[0], &a[end]);AdjustDown(a, end, 0); --end;}
}TOP-K问题
TOP-K问题:即求数据集合中前K个最大的元素或者最小的元素,一般情况下数据量都比较大。
1. 用数据集合中前K个元素来建堆
2. 用剩余的N-K个元素依次与堆顶元素来比较,不满足则替换堆顶元素

void CreateNDate()
{// 造数据int n = 10000000;srand(time(0));const char* file = "data.txt";FILE* fin = fopen(file, "w");if (fin == NULL){perror("fopen error");return;}for (int i = 0; i < n; ++i){int x = (rand()+i) % 10000000;fprintf(fin, "%d\n", x);}fclose(fin);
}void PrintTopK(const char* file, int k)
{FILE* fout = fopen(file, "r");if (fout == NULL){perror("fopen error");return;}// 建一个k个数小堆int* minheap = (int*)malloc(sizeof(int) * k);if (minheap == NULL){perror("malloc error");return;}// 读取前k个,建小堆for (int i = 0; i < k; i++){fscanf(fout, "%d", &minheap[i]);AdjustUp(minheap, i);}int x = 0;while (fscanf(fout, "%d", &x) != EOF){if (x > minheap[0]){minheap[0] = x;AdjustDown(minheap, k, 0);}}for (int i = 0; i < k; i++){printf("%d ", minheap[i]);}printf("\n");free(minheap);fclose(fout);
}int main()
{CreateNDate();PrintTopK("data.txt", 5);return 0;
}相关文章:

数据结构初阶:二叉树(一)
树概念及结构 树的概念 树是一种 非线性 的数据结构,它是由 n ( n>0 )个有限结点组成一个具有层次关系的集合。 把它叫做树是因 为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的 。 有一个特殊的结点&a…...
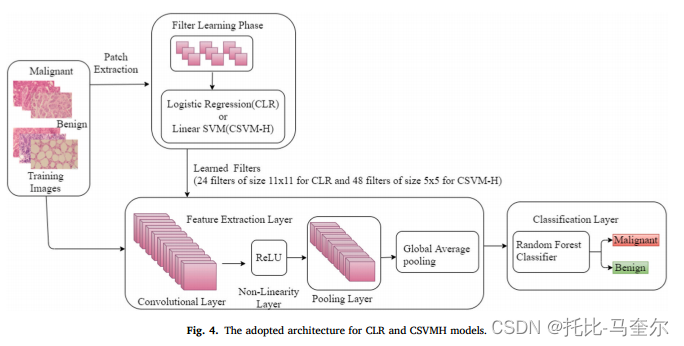
基于逻辑回归和支持向量机的前馈网络进行乳腺癌组织病理学图像分类
CNN(卷积神经网络)通过使用反向传播方法来学习特征,这种方法需要大量的训练数据,并且存在梯度消失问题,从而恶化了特征学习。 CNN卷积神经网络 CNN由一个多层神经网络组成,该网络从标记的训练数据集中学习…...

35-4 fastjson漏洞复现
环境准备:35-2 fastjson反序列化漏洞介绍 及漏洞环境搭建-CSDN博客 fastjson_tool.jar下载:fastjson_rce_tool: fastjson命令执行自动化利用工具, remote code execute,JNDI服务利用工具 RMI/LDAP (gitee.com) 一、攻击机kali开启nc监听6666端口(或其他端口也行,只要不…...

Qt-控件篇
QPushbutton 1、设置按钮文本 pushButton->setText("按钮"); 2、获取按钮文本 pushButton->text(); 3、设置按钮的大小为特定值(宽度和高度) pushButton->setFixedSize(width,height); 4、设置按钮悬停时的工具提示文本。 pushButto…...

实现 Table 的增加和删除,不依赖后端数据回显
需求 删除前 删除后 分析 首先写一个 Table <a-card style"width:100%"><template#extra><a-button type"text" click"addSelectItem" style"margin-right: 5px">添加</a-button><a-button type&quo…...
——三系统后端nodejs+express)
个人网站开发记录(七)——三系统后端nodejs+express
前言 这种已经完全工程化了的()后端其实已经没啥好说的了,因为就是单纯的写接口然后调用接口就完事了! 正文 唯一值得一提的大概是我在写这个系统的时候搞了https的链接,具体来说就是先申请一个ssl证书,…...

C#入门理解设计模式的6大原则
**设计模式的原则是指导设计模式创建和应用的基本原则,这些原则有助于创建灵活、可维护且可扩展的软件系统。**1. 单一职责原则(Single Responsibility Principle, SRP) 单一职责原则指出一个类应该只有一个引起它变化的原因。换句话说&…...

Linux如何切换root用户
Linux如何切换root用户 sudosudo -i想一直使用root权限,可以使用su命令 sudo 执行命令后,输入用户密码可以短暂的获取root权限 sudo -i 通过此命令直接输入当前管理员用户的密码就可以进入root用户了 想一直使用root权限,可以使用su命令 …...
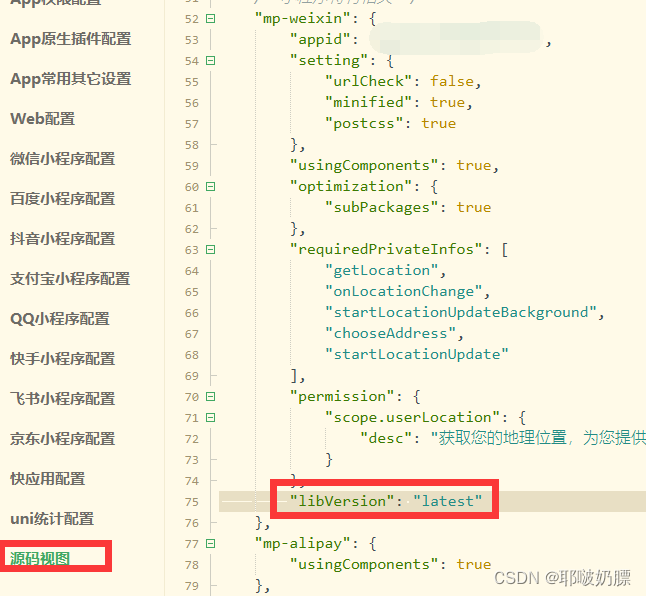
uniapp小程序编译报错
说明 微信小程序编译每次都出现[ project.config.json 文件内容错误] project.config.json: libVersion 字段需为 string, 解决 找到manifest.json文件 添加:"libVersion": "latest",重新编译即可。...

van-uploader 在app内嵌的webview中的一些坑
问题: 部分版本在ios 中没有问题,但是安卓中不触发图片选择和拍照(之前是可以的,可能是没有锁定版本,重新发版导致的)。在ios中下拉文案是英文,html配置lang等于 zh 也没有用,ios里…...

使用Kotlin进行全栈开发 Ktor+Kotlin/JS
首发于Enaium的个人博客 前言 本文将介绍如何使用 Kotlin 全栈技术栈KtorKotlin/JS来构建一个简单的全栈应用。 准备工作 创建项目 首先我们需要创建一个Kotlin项目,之后继续在其中新建两个子项目,一个是Kotlin/JS项目,另一个是Ktor项目。…...

数据结构_带头双向循环链表
List.h 相较于之前的顺序表和单向链表,双向链表的逻辑结构稍微复杂一些,但是在实现各种接口的时候是很简单的。因为不用找尾,写起来会舒服一点。(也可能是因为最近一直在写这个的原因) #pragma once #include<std…...

常见的垃圾回收器(下)
文章目录 G1ShenandoahZGC 常见垃圾回收期(上) G1 参数1: -XX:UseG1GC 打开G1的开关,JDK9之后默认不需要打开 参数2:-XX:MaxGCPauseMillis毫秒值 最大暂停的时间 回收年代和算法 ● 年轻代老年代 ● 复制算法 优点…...

网桥的原理
网桥的原理 1.1 桥接的概念 简单来说,桥接就是把一台机器上的若干个网络接口“连接”起来,其结果是,其中一个网口收到的报文会被复制给其他网口并发送出去。以使得网口之间的报文能够互相转发。 交换机有若干个网口,并且这些…...

STM32 CAN过滤器细节
STM32 CAN过滤器细节 简介 每组筛选器包含2个32位的寄存器,分别为CAN_FxR1和CAN_FxR2,它们用来存储要筛选的ID或掩码 四种模式 模式说明32位掩码模式CAN_FxR1存储ID, CAN_FxR2存储哪个位必须要与CAN_FxR1中的ID一致 , 2个寄存器…...
网络编程(现在不重要)
目录 网络编程三要素与InetAddress类的使用 软件架构 面临的主要问题 网络编程三要素(对应三个问题) InetAddress的使用 TCP与UDP协议剖析与TCP编程案例(了解) TCP协议 UDP协议 例子 UDP、URL网络编程 URL:&…...
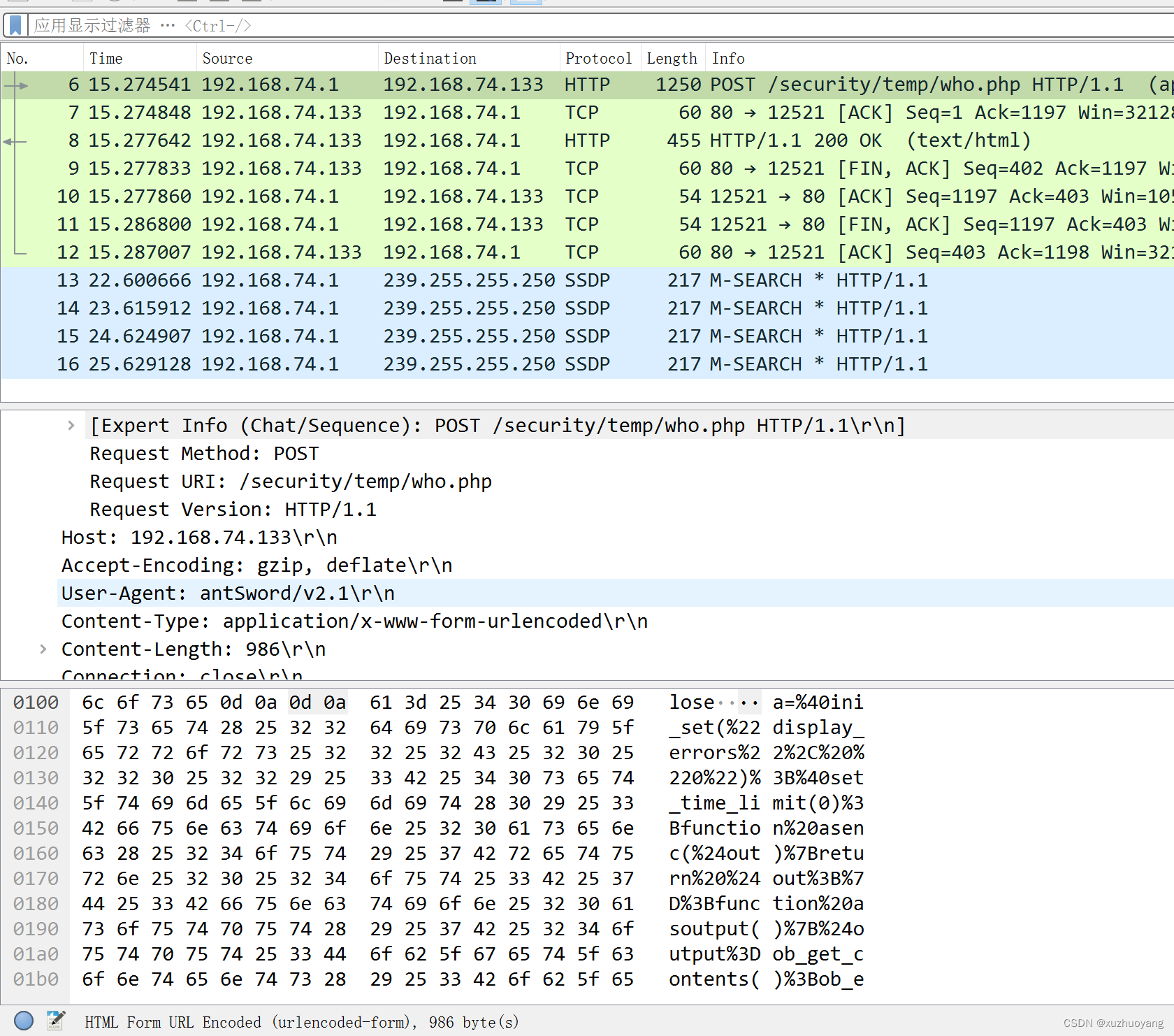
10-菜刀连接木马
找到了漏洞后,并且上传了木马之后才能使用的两款工具 中国菜刀和冰蝎 想办法获取别人的cookie,cookie中有session-id 一、中国菜刀 1、必须提前已经完成木马植入然后才能使用 2、木马必须是POST请求,参数自定义,在菜刀里给出…...

Unity数据持久化—Json存档
项目需求为: 1.实现存档列表,显示存档截图,可以查看之前保存的所有存档 2.点击存档直接加载到场景 首先,定义两个类,用于声明存档列表和存档所需要的List [System.Serializable] public class SaveData {//存储目标…...
基于SSM的在线学习系统的设计与实现(论文+源码)_kaic
基于SSM的在线学习系统的设计与实现 摘要 随着信息互联网购物的飞速发展,一般企业都去创建属于自己的管理系统。本文介绍了在线学习系统的开发全过程。通过分析企业对于在线学习系统的需求,创建了一个计算机管理在线学习系统的方案。文章介绍了在线学习系…...

数据库SQL语言实战(二)
目录 检索查询 题目一 题目二 题目三 题目四 题目五 题目六 题目七 题目八 题目九(本篇最难的题目) 分析 实现(两种方式) 模板 总结 检索查询 按照要求查找数据库中的数据 题目一 找出没有选修任何课程的学…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...



