算法训练营第二十天 | LeetCode 110平衡二叉树、LeetCode 257 二叉树的所有路径、LeetCode 404 左叶子之和
LeetCode 110 平衡二叉树
递归写法很简单,直接自底向上每个节点判断是否为空,为空说明该层高度为0。不为空用一个int型变量l记录左子树高度(递归调用该函数自身),一个int型变量r记录右子树高度(同样递归调用该函数自身),将l和r相减取绝对值,大于1说明不平衡直接返回-1,此外还需要判断l和r是否已经是-1,这种情况下也直接返回-1。这样判断的底层原理是计算每个节点返回值是高度还是-1,取-1也是因为不会影响到正常高度的计算。最后来到递归遍历阶段,返回1+max(l,r)即可。
这个过程中,最上层是确认返回条件,中间是确认参数和返回值,最下层是递归逻辑。
代码如下:
class Solution {
public:int height(TreeNode* root) {if (!root) return 0; int l = height(root->left), r = height(root->right);if (abs(l - r) > 1) return -1;else if (l == -1) return -1;else if (r == -1) return -1;return 1 + max(l, r); }bool isBalanced(TreeNode* root) {if (height(root) != -1) return true;else return false;}
};LeetCode 257 二叉树的所有路径
这题对于学过回溯法的人来说,很明显是回溯了。新手可能会有点头痛。
回溯法本质上也是一种递归,是一种暴力枚举。在递归过程中,如果没有后续状态就会把当前这一条路径放进存储结果的集合中,返回当前函数到上一层。而如果有后续状态,就先记录当前路径,将当前路径加上其中一个下一状态,用这一路径继续递归,直到返回,在其语句后面还要将路径还原至递归前。相当于先给你一个苹果,让你吃完之后看苹果是啥样子,记录下来,再一路回到你吃苹果之前,把苹果给别人吃,看又是啥样子。这样的递归过程就能实现一种暴力枚举。
代码如下:
class Solution {
private:vector<string> res;string path = "";
public:void backtracking(TreeNode* cur) {if (!cur->left && !cur->right) {res.push_back(path);}else {if (cur) {string temp = path;if (cur->left) {string s = to_string(cur->left->val);path += "->";path += s;backtracking(cur->left);path = temp;}if (cur->right) {string s = to_string(cur->right->val);path += "->";path += s;backtracking(cur->right);path = temp;}}}}vector<string> binaryTreePaths(TreeNode* root) {if (!root) return res;string s = to_string(root->val);path += s;backtracking(root);return res;}};还需要注意的有递归起始状态,返回条件和每次递归逻辑的确定。
本题还可以尝试迭代法来写。暂时先放这,等会来写。
LeetCode 404 左叶子之和
其实前序遍历等遍历方式中选一种就行了,需要注意的是左叶子首先要是某个叶子的左节点,然后还要是叶子节点。可以顺便满足这个遍历情况的,前序遍历是肯定可以的。中序遍历也可以,层序遍历和后续遍历会比较麻烦一点。这里给出前序遍历实现的代码如下:
class Solution {
public:int sumOfLeftLeaves(TreeNode* root) {int sum = 0;TreeNode* cur = root;queue<TreeNode*> myque;while (cur || !myque.empty()) {while (cur) {myque.push(cur);if (cur->left) {if (!cur->left->left && !cur->left->right)sum += cur->left->val;}cur = cur->left;}cur = myque.front();myque.pop();cur = cur->right;}return sum;}
};相关文章:

算法训练营第二十天 | LeetCode 110平衡二叉树、LeetCode 257 二叉树的所有路径、LeetCode 404 左叶子之和
LeetCode 110 平衡二叉树 递归写法很简单,直接自底向上每个节点判断是否为空,为空说明该层高度为0。不为空用一个int型变量l记录左子树高度(递归调用该函数自身),一个int型变量r记录右子树高度(同样递归调…...

Docker:centos7安装docker
官网:https://www.docker.com/官网 文档地址 - 确认centos7及其以上的版本 查看当前系统版本 cat /etc/redhat-release- 卸载旧版本 依照官网执行 - yum安装gcc相关 yum -y install gccyum -y install gcc-c- 安装需要的软件包 yum install -y yum-utils- 设置s…...

EasyExcel导出工具类
目录 工具类 头部实体类(要和工具类在同一个module或项目下) 日期转换器 工具类 /*** 导出Excel工具类*/ public class EasyExcelUtil<T> {/*** 单sheet(Map写入)* param response 响应对象* param headList 头部集合* p…...

【Godot4.2】EasyTreeData通用解析
概述 之前在《【Godot4.2】Tree控件自定义树形数据ETD及其解析》一文中,实现了对带缩进的层级结构文本的解析,并将其用于Tree控件的列表项构造。 不过当时并没有实现专门的类,今天花了一点时间实现了一下。现在可以更方便的构造和解析ETD数…...
力扣每日一题109:有序链表转换二叉搜索树
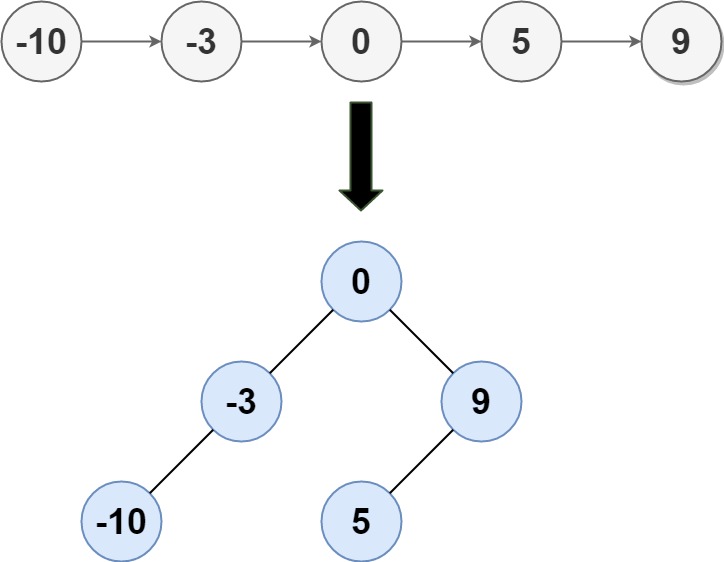
题目 中等 给定一个单链表的头节点 head ,其中的元素 按升序排序 ,将其转换为 平衡 二叉搜索树。 示例 1: 输入: head [-10,-3,0,5,9] 输出: [0,-3,9,-10,null,5] 解释: 一个可能的答案是[0,-3,9,-10,null,5],它…...

企业计算机服务器中了locked勒索病毒怎么处理,locked勒索病毒解密建议
随着互联网技术在企业当中的应用,越来越多的企业利用网络开展各项工作业务,网络为企业提供了极大便利,也大大加快了企业发展步伐,提高了企业生产办公效率。但网络技术的发展也为企业的数据安全带来严重威胁。近期,云天…...
开源推荐榜【MalusAdmin基于 Vue3/TypeScript/NaiveUI 和 NET7 Sqlsugar 开发的后台管理框架】
简介 Malus是海棠的意思,顾名思义,海棠后台管理系统,读音与【马卢斯】相近,也可称作为马卢斯后台管理系统。 基于NET Core | NET7/8 & Sqlsugar | Vue3 | vite4 | TypeScript | NaiveUI 开发的前后端分离式权限管理系统,采用…...
批量抓取某电影网站的下载链接
思路: 进入电影天堂首页,提取到主页面中的每一个电影的背后的那个urL地址 a. 拿到“2024必看热片”那一块的HTML代码 b. 从刚才拿到的HTML代码中提取到href的值访问子页面,提取到电影的名称以及下载地址 a. 拿到子页面的页面源代码 b. 数据提…...

2024-05-06 问AI: 介绍一下深度学习中的LSTM网络
文心一言 当谈到深度学习中的LSTM(Long Short-Term Memory)网络时,它是一种特殊的循环神经网络(RNN)架构,旨在解决传统RNN在处理长序列时遇到的梯度消失和梯度爆炸问题。LSTM网络因其能够捕捉序列数据中的…...

二、Redis五种常用数据类型-String
1、用途 简单的K-V缓存计数器分布式锁session共享分布式ID生成(自增) 2、底层实现结构 Redis底层是c语言实现的,但是并没有使用c的string来表示字符串,而是使用自己的简单动态字符串的抽象类型(simple dynamic string,SDS)。 SDS结构: st…...
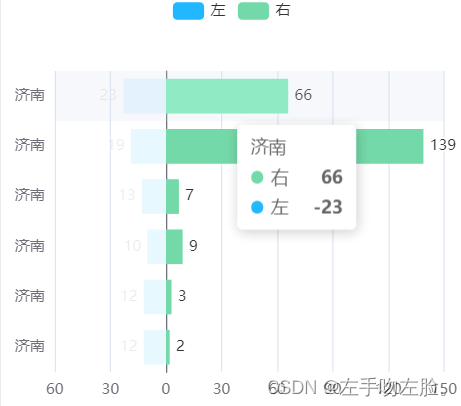
echarts柱状图实现左右横向对比
实现效果如上图 其实是两组数据,其中一组数据改为负数,然后 在展示的时候,在将负数取反 第一处修改坐标轴 xAxis: [{type: value,axisLabel: {formatter: function (value) {if (value < 0) {return -value;}else{return value;}}}}], 第…...
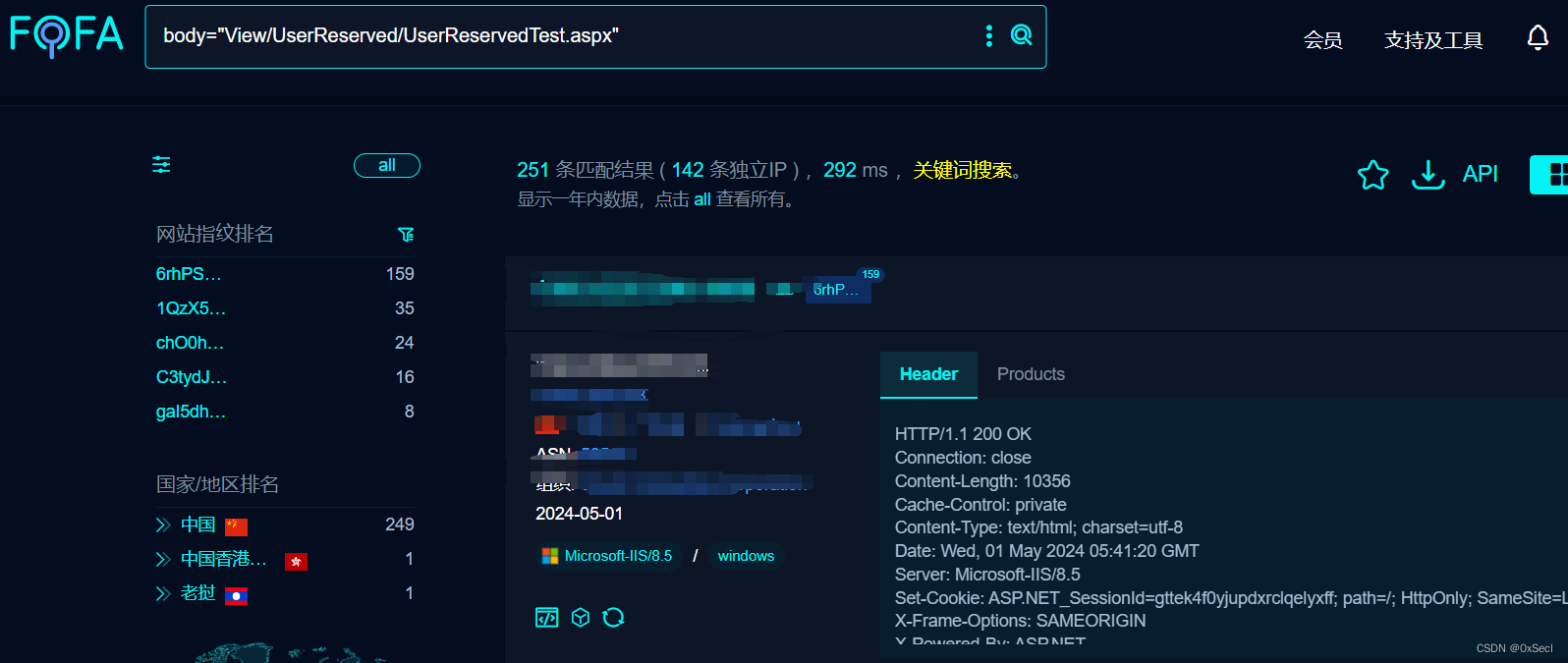
脸爱云一脸通智慧管理平台 SystemMng 管理用户信息泄露漏洞(XVE-2024-9382)
0x01 产品简介 脸爱云一脸通智慧管理平台是一套功能强大,运行稳定,操作简单方便,用户界面美观,轻松统计数据的一脸通系统。无需安装,只需在后台配置即可在浏览器登录。 功能包括:系统管理中心、人员信息管理中心、设备管理中心、消费管理子系统、订餐管理子系统、水控管…...

spring笔记2
一、基于xml的AOP实现 基于注解管理Bean,注解扫描 <context:component-scan base-package"com.zhou.spring.aop.xml"></context:component-scan><aop:config> <!-- 设置一个公共的切入点表达式--><aop:pointcut id&q…...

【挑战30天首通《谷粒商城》】-【第一天】02、简介-项目整体效果展示
文章目录 课程介绍 ( 本章了解即可,可以略过)一、 分布式基础 (全栈开发篇) (初中级)二、 分布式高级 (微服务架构篇) ( 高级)三、高可用集群 (架构师提升篇)( 架构 ) one more thing 课程介绍 ( 本章了解即可,可以略过) 1.分布式基础(全栈开发篇)2.分布…...
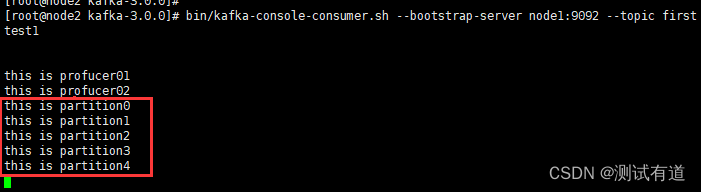
Kafka 生产者应用解析
目录 1、生产者消息发送流程 1.1、发送原理 2、异步发送 API 2.1、普通异步发送 2.2、带回调函数的异步发送 3、同步发送 API 4、生产者分区 4.1、分区的优势 4.2、生产者发送消息的分区策略 示例1:将数据发往指定 partition 示例2:有 key 的…...
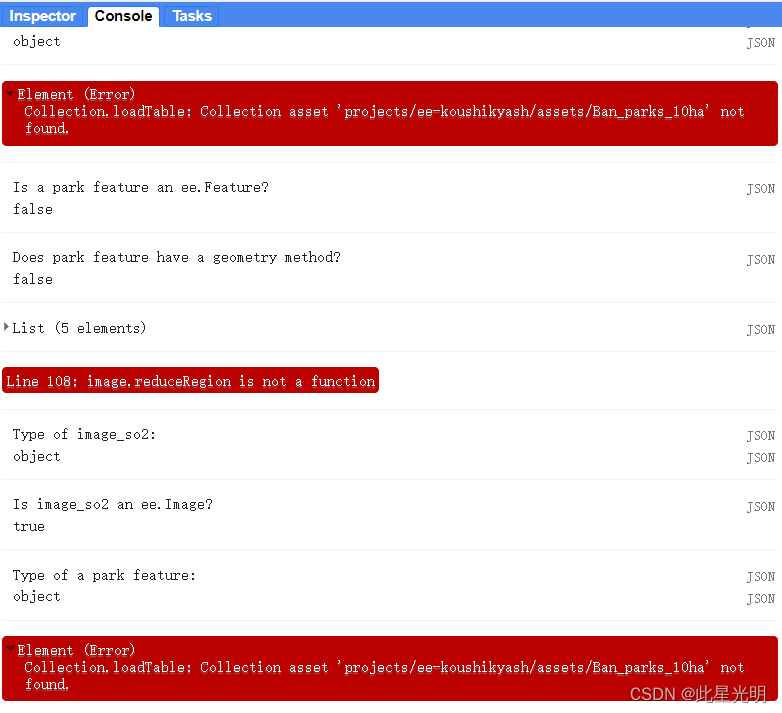
GEE错误——image.reduceRegion is not a function
简介 image.reduceRegion is not a function 这里的主要问题是我们进行地统计分析的时候,我们的作用对象必须是单景影像,而不是影像集合 错误"image.reduceRegion is not a function" 表示你正在尝试使用reduceRegion()函数来处理图像数据&…...

rk356x 关于yocto编译linux及bitbake实用方法
Yocto 完整编译 source oe-init-build-envbitbake core-image-minimalYocto 查询包名 bitbake -s | grep XXX // 获取rockchip相关包 :~/rk3568/yocto$ bitbake -s | grep rockchip android-tools-conf-rockchip :1.0-r0 gstreamer1.0-rockchip …...

Chrome您的连接不是私密连接 |输入“thisisunsafe”命令绕过警告or添加启动参数
一、输入 thisisunsafe 在当前页面用键盘输入 thisisunsafe ,不是在地址栏输入(切记),就直接敲键盘就行了 因为Chrome不信任这些自签名ssl证书,为了安全起见,直接禁止访问了,thisisunsafe 这个命令,说明你…...

牛客面试前端1
HTML语义化 是什么 前端语义化是指在构建网页时多使用html语义化标签布局,多使用带有语义的标签如header,aside,footer等标签为什么 结构清晰利于开发者开发与维护 有利于seo搜索引擎优化 有利于在网络卡顿时,正常显示页面结构&a…...
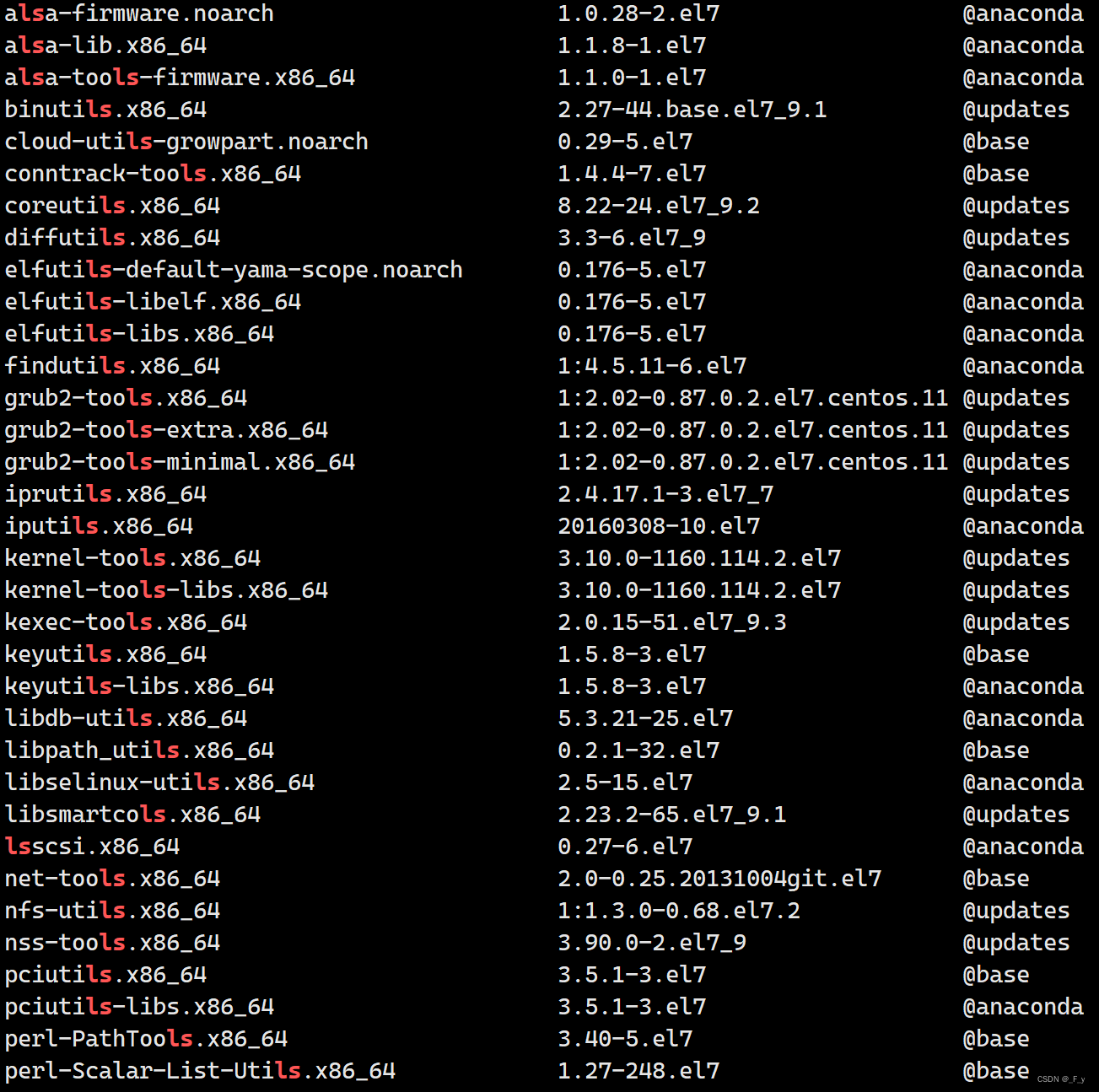
Linux的软件包管理器-yum
文章目录 软件包的概念yum源的配置的原因yum的使用查看软件包安装软件卸载软件 软件包的概念 软件包(SoftWare Package)是指具有特定的功能,用来完成特定任务的一个程序或一组程序。可分为应用软件包和系统软件包两大类 在Linux系统中,下载安装软件的方式…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...

MySQL的pymysql操作
本章是MySQL的最后一章,MySQL到此完结,下一站Hadoop!!! 这章很简单,完整代码在最后,详细讲解之前python课程里面也有,感兴趣的可以往前找一下 一、查询操作 我们需要打开pycharm …...

【实施指南】Android客户端HTTPS双向认证实施指南
🔐 一、所需准备材料 证书文件(6类核心文件) 类型 格式 作用 Android端要求 CA根证书 .crt/.pem 验证服务器/客户端证书合法性 需预置到Android信任库 服务器证书 .crt 服务器身份证明 客户端需持有以验证服务器 客户端证书 .crt 客户端身份…...

数据结构:泰勒展开式:霍纳法则(Horner‘s Rule)
目录 🔍 若用递归计算每一项,会发生什么? Horners Rule(霍纳法则) 第一步:我们从最原始的泰勒公式出发 第二步:从形式上重新观察展开式 🌟 第三步:引出霍纳法则&…...

GAN模式奔溃的探讨论文综述(一)
简介 简介:今天带来一篇关于GAN的,对于模式奔溃的一个探讨的一个问题,帮助大家更好的解决训练中遇到的一个难题。 论文题目:An in-depth review and analysis of mode collapse in GAN 期刊:Machine Learning 链接:...
