docker部署的nacos2.2x开启鉴权功能
注意在2.2.0版本之后如果不开启鉴权,那么默认不需要登录就可以访问


所以我们需要手动开启鉴权,nacos启动好以后来到容器内部修改
docker exec -it nacos /bin/shvim conf/application.properties在第34行下面添加
nacos.core.auth.enabled=true
nacos.core.auth.enable.userAgentAuthWhite=false然后修改下面这三行nacos.core.auth.plugin.nacos.token.secret.key=${NACOS_AUTH_TOKEN:SecretKey13213464979879798431316877979798464654987979846516565987987}SecretKey13213464979879798431316877979798464654987979846516565987987的内容可以自定义nacos.core.auth.server.identity.key=${NACOS_AUTH_IDENTITY_KEY:example}
nacos.core.auth.server.identity.value=${NACOS_AUTH_IDENTITY_VALUE:example}
docker restart nacos
修改完后退出容器,然后重启nacos重新访问就可以正常登录了,第一次访问会有一个没有命名空间权限的报错这个点击确定不用管直接登录。
http://192.168.81.130:8848/nacos
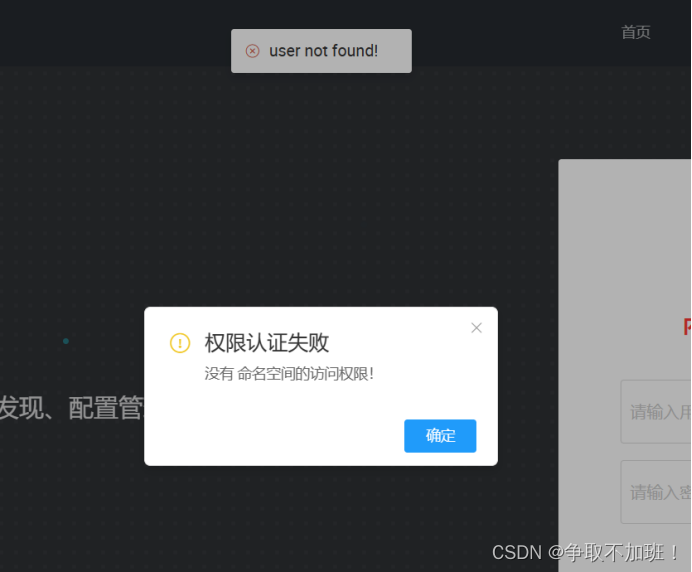
或者在访问时http://192.168.81.130:8848/nacos/#/login 这样就不会弹窗了
阿里云给出的问题回复是:Nacos 2.2.3 开启鉴权后首次登录报“权限认证失败,没有命名空间的访问权限”,但第二次登录就恢复正常的原因可能是因为首次登录时用户的权限尚未完全生效或同步到服务端。
在Nacos开启鉴权后,系统会要求每个用户拥有对应的权限才能访问特定的命名空间。当用户第一次登录时,特别是刚创建或刚刚赋予权限的用户,可能会存在一定的延迟。
默认用户nacos 默认密码 nacos
到这里nacos鉴权就开启成功了。
相关文章:

docker部署的nacos2.2x开启鉴权功能
注意在2.2.0版本之后如果不开启鉴权,那么默认不需要登录就可以访问 所以我们需要手动开启鉴权,nacos启动好以后来到容器内部修改 docker exec -it nacos /bin/shvim conf/application.properties在第34行下面添加 nacos.core.auth.enabledtrue nacos.cor…...

【数据结构与算法】之五道链表进阶面试题详解!
目录 1、链表的回文结构 2、相交链表 3、随机链表的复制 4、环形链表 5、环形链表(||) 6、完结散花 个人主页:秋风起,再归来~ 数据结构与算法 个人格言:悟已往之不谏,知…...
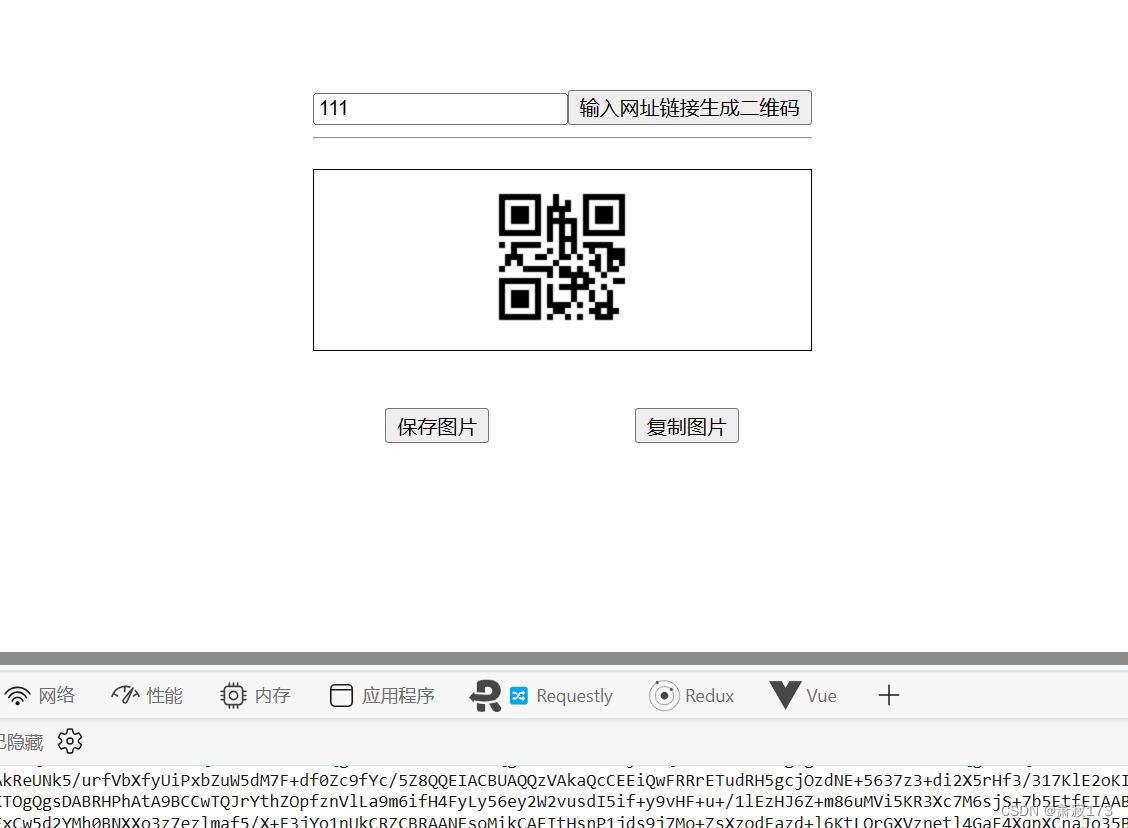
vue2实现生成二维码和复制保存图片功能(复制的同时会给图片加文字)
<template><divstyle"display: flex;justify-content: center;align-items: center;width: 100vw;height: 100vh;"><div><!-- 生成二维码按钮和输入二维码的输入框 --><input v-model"url" placeholder"输入链接" ty…...

Redis之字符串类型深入之SDS底层结构
作为一名程序员不可能不知道redis 知道redis不可能不知道redis的字符串 如果你真的熟悉redis不能不知道sds, 我们探究一下redis字符串的底层结构 sds翻译过来就是动态扩容(Simple Dynamic String)、先看一下最早版本redis的sds结构体 struct sdshdr{int len; //记录数组中…...

Cesium 3dTileset 支持 uv 和 纹理贴图
原理: 使用自定义shader实现uv自动计算 贴图效果: uv效果:...

C++可变参数模板中的省略号
看可变参数模板代码时常会遇到省略号的使用,这类奇特的“...”出现位置还不固定,容易引起困惑。C最近一直不用都快废了,在此想对省略号的使用做个简单归纳以提醒自己。可变参数模板以两种方式使用省略号。 在参数名称的左侧,表示“…...
uni-ui 使用uni-icons有些图标显示不出来,如down,up图标
问题描述 我使用的是uni创建时勾选的uni-ui模板,一次偶然机会发现down图标显示不出,left,right等其他图标又可以。 最后发现使用uni-icons不是最新版本导致的,使用模板生成的icons是1.3.5版本,我在插件市场找到的是2.0…...

动态增删表格
期望目标:实现一个能通过按钮来动态增加表格栏,每次能添加一行,每行末尾有一个删减按钮。 <el-button type"text" class"primary"click"addMember()">添加</el-button> <el-table:data"m…...
Java-(乘法表之后)增强for循环
这里我们先做个了解,之后我会在数组中进行详细介绍Java5引入了一种主要用于数组或集合的增强型for循环Java增强型for循环语法格式如下 For(声明语句:表达式){ //代码语句 } 声明语句:声明新的局部变量,该变量的类型…...
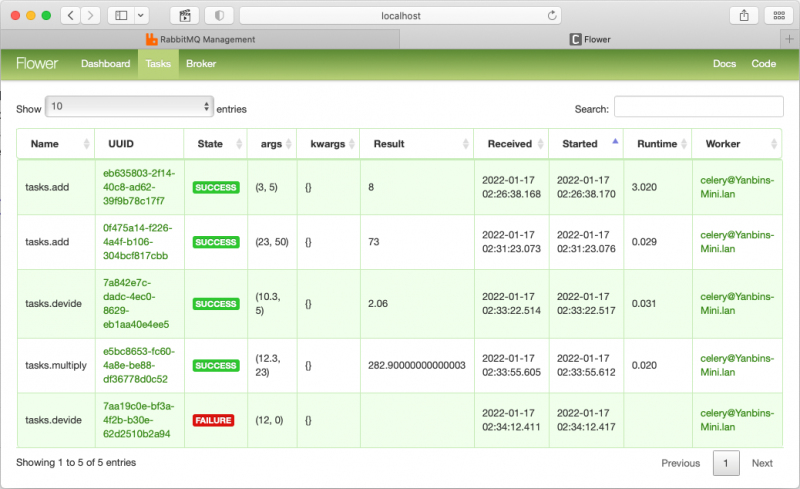
Celery(分布式任务队列)入门学习笔记
Celery 的简单介绍 用 Celery 官方的介绍:它是一个分布式任务队列; 简单,灵活,可靠的处理大量消息的分布式系统; 它专注于实时处理,并支持任务调度。 Celery 如果使用 RabbitMQ 作为消息系统的话,整个应用体系就是下…...

【网络】tcp协议如何保证可靠性
TCP(Transmission Control Protocol)是一种面向连接的、可靠的传输层协议,为网络通信提供了可靠性和连接稳定性。本文将详细介绍 TCP 协议如何保证数据的可靠传输和连接的稳定性,并分析其优缺点。 可靠性保证 序号和确认机制&…...
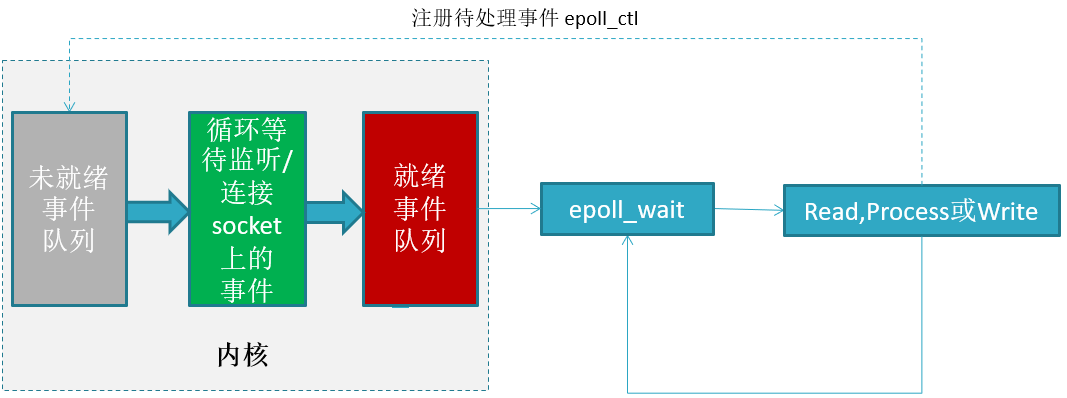
select,poll,epoll
在 Linux Socket 服务器短编程时,为了处理大量客户的连接请求,需要使用非阻塞I/O和复用,select,poll 和 epoll 是 Linux API 提供的I/O复用方式。 \selectpollepoll操作方式遍历遍历回调底层实现数组链表哈希表IO效率每次调用都进…...

【48天笔试强训】day18
题目1 描述 有一种兔子,从出生后第3个月起每个月都生一只兔子,小兔子长到第三个月后每个月又生一只兔子。 例子:假设一只兔子第3个月出生,那么它第5个月开始会每个月生一只兔子。 一月的时候有一只兔子,假如兔子都…...
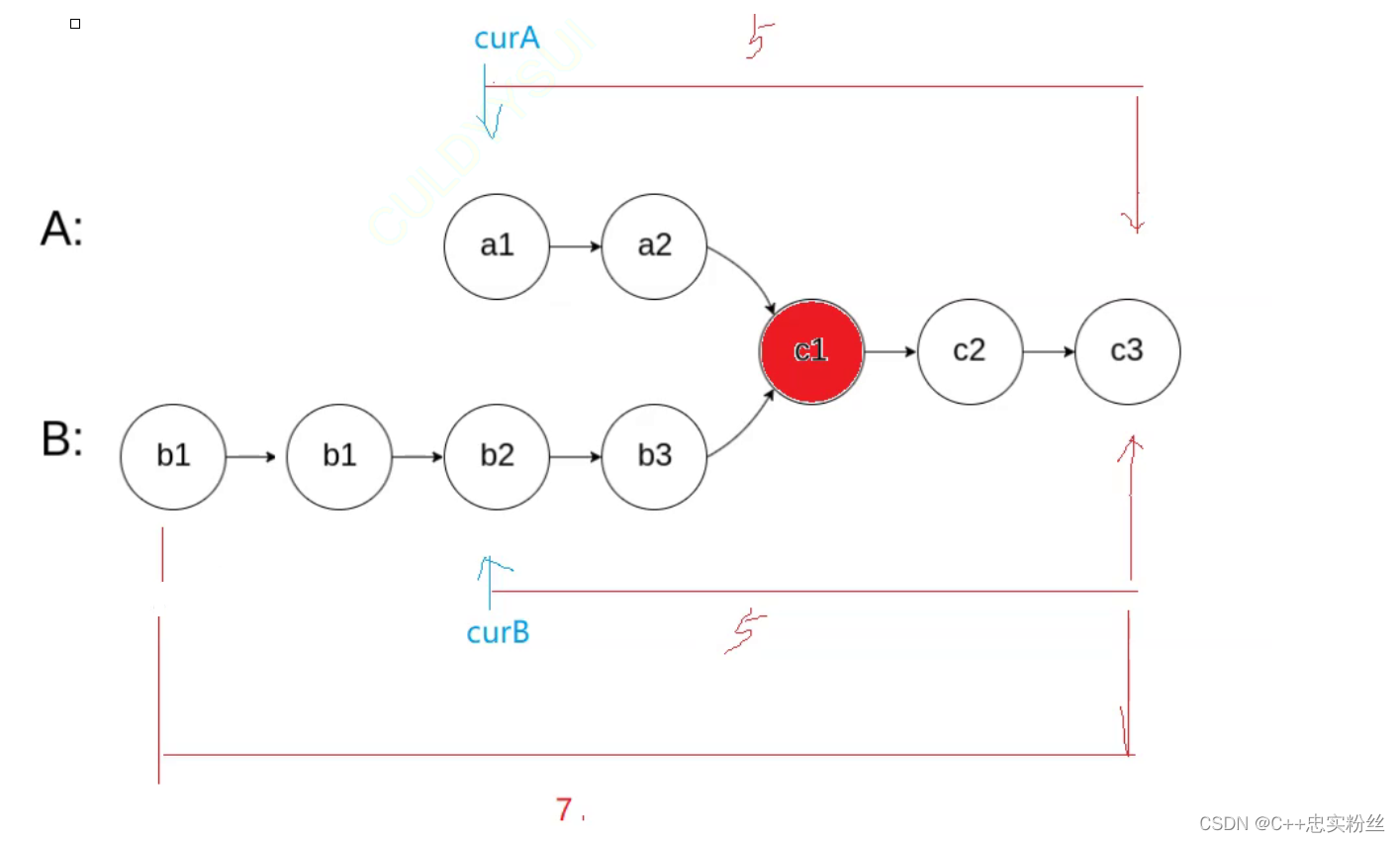
链表经典面试题01
目录 引言 面试题01:返回倒数第k个节点 题目描述: 思路分析: 代码展示: 面试题02:链表的回文结构 题目描述: 描述 思路分析: 代码展示: 面试题03:相交链表 题目描述: 思路分析: 代码展示: 小结: 引言 这次的题均来自力扣和牛客有关链表的经典面试题,代码只会展示…...
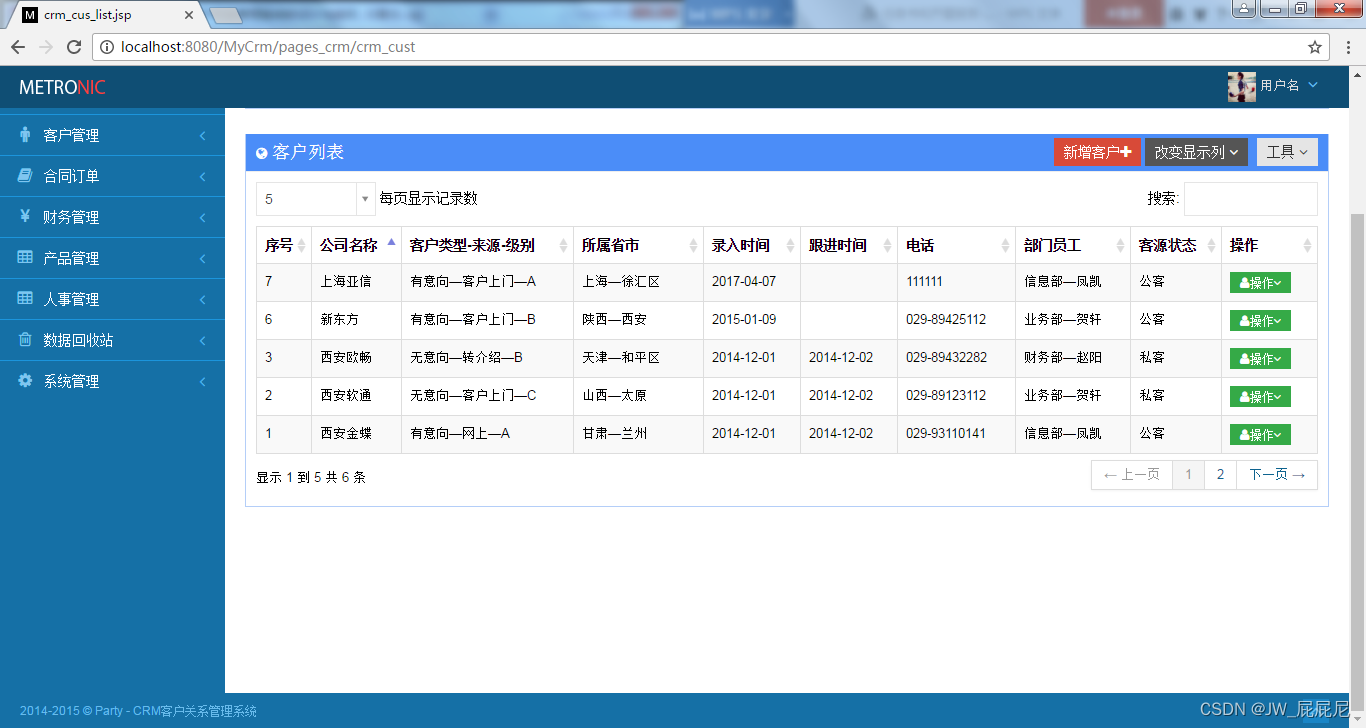
基于java的CRM客户关系管理系统的设计与实现(论文 + 源码 )
【免费】基于Java的CRM客户关系管理系统的设计和实现.zip资源-CSDN文库https://download.csdn.net/download/JW_559/89273409 基于Java的CRM客户关系管理系统的设计与实现 摘 要 随着互联网的高速发展,市场经济的信息化,让企业之间的竞争变得࿰…...

【动态规划-最长上升子序列模型part2】:拦截导弹、导弹防御系统、最长公共上升子序列【已更新完成】
1、拦截导弹 某国为了防御敌国的导弹袭击,发展出一种导弹拦截系统。 但是这种导弹拦截系统有一个缺陷:虽然它的第一发炮弹能够到达任意的高度,但是以后每一发炮弹都不能高于前一发的高度。 某天,雷达捕捉到敌国的导弹来袭。 由于…...

Spring 如何解决 Bean 循环依赖
循环依赖解释 bean A 属性注入时依赖bean B ,并且bean B属性注入时也依赖bean A ,造成 bean A 和bean B 都无法完成初始化问题,形成了闭环。 注意 项目中存在Bean的循环依赖,是Bean对象职责划分不明确、代码质量不高的表现&#…...
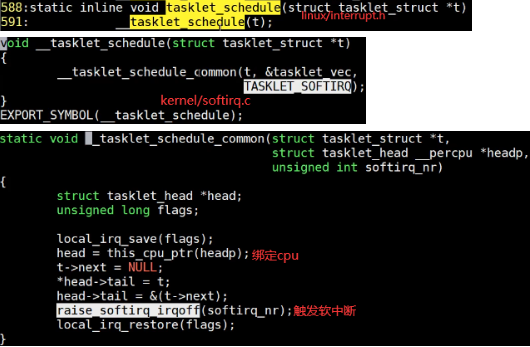
【driver4】锁,错误码,休眠唤醒,中断,虚拟内存,tasklet
文章目录 1.互斥锁和自旋锁选择:自旋锁(开销少)的自旋时间和被锁住的代码执行时间成正比关系2.linux错误码:64位系统内核空间最后一页地址为0xfffffffffffff000~0xffffffffffffffff,这段地址是被保留的,如果…...

python之 函数相关知识解析
01 函数的注释与嵌套 1.函数的注释 函数的注释与普通注释的区别:用来说明当前函数的参数含义 param 参数名: 参数的注释信息 return: 函数的返回值 例如: def fun1(name):""":param name: 参数的注释信息:return: 函数的返回值"…...
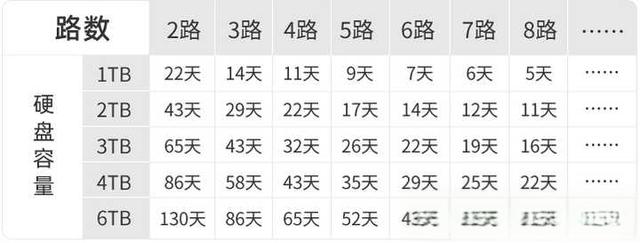
监视器和显示器的区别,普通硬盘和监控硬盘的区别
监视器与显示器的区别,你真的知道吗? 中小型视频监控系统中,显示系统是最能展现效果的一个重要环节,显示系统的优劣将直接影响视频监控系统的用户体验满意度。 中小型视频监控系统中,显示系统是最能展现效果的一个重要…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...

redis和redission的区别
Redis 和 Redisson 是两个密切相关但又本质不同的技术,它们扮演着完全不同的角色: Redis: 内存数据库/数据结构存储 本质: 它是一个开源的、高性能的、基于内存的 键值存储数据库。它也可以将数据持久化到磁盘。 核心功能: 提供丰…...

【WebSocket】SpringBoot项目中使用WebSocket
1. 导入坐标 如果springboot父工程没有加入websocket的起步依赖,添加它的坐标的时候需要带上版本号。 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-websocket</artifactId> </dep…...

webpack面试题
面试题:webpack介绍和简单使用 一、webpack(模块化打包工具)1. webpack是把项目当作一个整体,通过给定的一个主文件,webpack将从这个主文件开始找到你项目当中的所有依赖文件,使用loaders来处理它们&#x…...

2.2.2 ASPICE的需求分析
ASPICE的需求分析是汽车软件开发过程中至关重要的一环,它涉及到对需求进行详细分析、验证和确认,以确保软件产品能够满足客户和用户的需求。在ASPICE中,需求分析的关键步骤包括: 需求细化:将从需求收集阶段获得的高层需…...

算法250609 高精度
加法 #include<stdio.h> #include<iostream> #include<string.h> #include<math.h> #include<algorithm> using namespace std; char input1[205]; char input2[205]; int main(){while(scanf("%s%s",input1,input2)!EOF){int a[205]…...

大模型真的像人一样“思考”和“理解”吗?
Yann LeCun 新研究的核心探讨:大语言模型(LLM)的“理解”和“思考”方式与人类认知的根本差异。 核心问题:大模型真的像人一样“思考”和“理解”吗? 人类的思考方式: 你的大脑是个超级整理师。面对海量信…...
