2024数学-微积分和线性代数/本科研究生专业考试/考研/论文/重点公式考点汇总/最难公式投票
## 整体公式汇总列表
http://www.deepnlp.org/equation/category/math
#### 微积分
## 几何级数
http://www.deepnlp.org/equation/arithmetic-and-geometric-progressions
## 级数收敛
http://www.deepnlp.org/equation/convergence-of-series
## 二项式展开
http://www.deepnlp.org/equation/binomial-expansion
## 泰勒展开
http://www.deepnlp.org/equation/taylor-series
## 高斯过程
http://www.deepnlp.org/equation/gaussian-process
# 傅里叶级数
http://www.deepnlp.org/equation/fourier-series
# maclaurin级数
http://www.deepnlp.org/equation/maclaurin-series
# 复数级数
http://www.deepnlp.org/equation/power-series-for-complex-variables
# 拉普拉斯方程
http://www.deepnlp.org/equation/laplace-equation
# 拉普拉斯变换
http://www.deepnlp.org/equation/laplace-transform
##### 代数Algebra
# 行列式 Determinants
http://www.deepnlp.org/equation/determinants-of-a-matrix
# 特征值和特征向量
http://www.deepnlp.org/equation/eigenvalues-and-eigenvectors
# 二项式回归
http://www.deepnlp.org/equation/regression-least-squares-fitting
# 傅里叶变换
http://www.deepnlp.org/equation/fourier-transforms
相关文章:

2024数学-微积分和线性代数/本科研究生专业考试/考研/论文/重点公式考点汇总/最难公式投票
## 整体公式汇总列表 http://www.deepnlp.org/equation/category/math #### 微积分 ## 几何级数http://www.deepnlp.org/equation/arithmetic-and-geometric-progressions ## 级数收敛http://www.deepnlp.org/equation/convergence-of-series ## 二项式展开 http://www.dee…...
:Leetcode1005、134、135(难得有一天能完全独立做出题目))
代码随想录训练营Day33(贪心算法):Leetcode1005、134、135(难得有一天能完全独立做出题目)
Leetcode1005: 题目描述: 给你一个整数数组 nums 和一个整数 k ,按以下方法修改该数组: 选择某个下标 i 并将 nums[i] 替换为 -nums[i] 。 重复这个过程恰好 k 次。可以多次选择同一个下标 i 。 以这种方式修改数组后,返回数…...
Flutter笔记:Widgets Easier组件库(12)使用消息吐丝(Notify Toasts)
Flutter笔记 Widgets Easier组件库(12)使用消息吐丝(Notify Toasts) - 文章信息 - Author: 李俊才 (jcLee95) Visit me at CSDN: https://jclee95.blog.csdn.netMy WebSite:http://thispage.tech/Email: 29114848416…...

从《春色寄情人》学习如何面对死亡
经典台词,很震撼又很实用,记录一下。 ❤️01 有的时候好人不长命百岁,是因为老天爷觉得他们太累,让他们提前休息了! ❤️02 跟我们亲近的人离世,有可能是老天给我们发的信号,提醒我们ÿ…...

使用moveit控制机械臂
在这篇博客中,我们将详细探讨如何利用Python和Robot Operating System(ROS)配合MoveIt! 控制机械臂执行精确的抓取任务。机械臂技术在工业自动化、医疗服务以及研究领域扮演着越来越关键的角色。本文将通过介绍安装必要的软件、编写控制脚本以…...
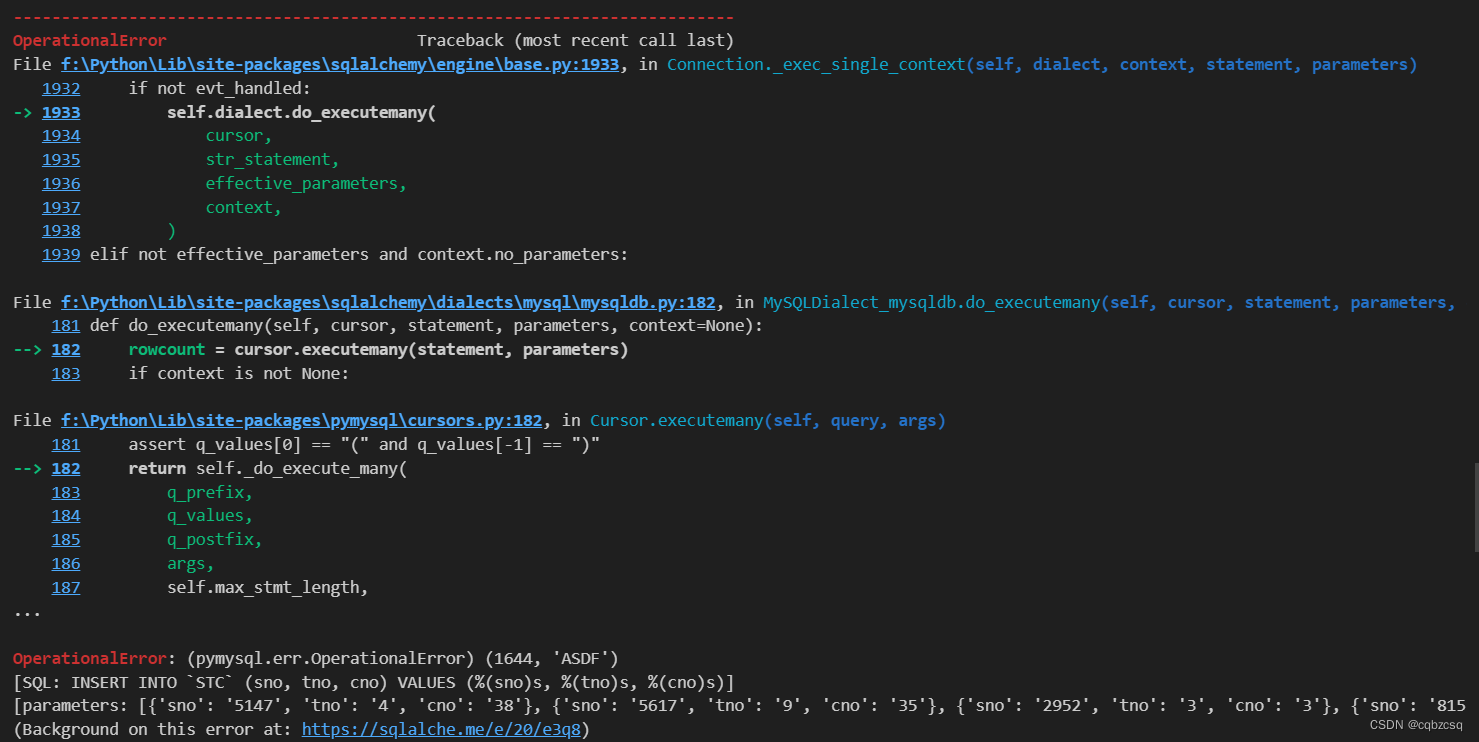
Mysql报错红温集锦(一)(ipynb配置、pymysql登录、密码带@、to_sql如何加速、触发器SIGNAL阻止插入数据)
一、jupyter notebook无法使用%sql来添加sql代码 可能原因: 1、没装jupyter和notebook库、没装ipython-sql库 pip install jupyter notebook ipython-sql 另外如果是vscode的话还需要安装一些相关的插件 2、没load_ext %load_ext sql 3、没正确的登录到mysql…...

ASP.NET Core SignalR 配置与集成测试究极指南
这篇文章也可以在我的博客中查看 前言 哥们最近都在埋头苦干,沉默是金,有一段时间没更新博客了。然而今儿SignalR集成测试实属是给我整破防了。虽说SignalR是.NET官方维护的实时通信库,已经开发了有十几年,甚至已经编入至了core…...
JENKINS 安装,学习运维从这里开始
Download and deployJenkins – an open source automation server which enables developers around the world to reliably build, test, and deploy their softwarehttps://www.jenkins.io/download/首先点击上面。下载Jenkins 为了学习,从windows开始&#x…...

大语言模型从Scaling Laws到MoE
1、摩尔定律和伸缩法则 摩尔定律(Moores law)是由英特尔(Intel)创始人之一戈登摩尔提出的。其内容为:集成电路上可容纳的晶体管数目,约每隔两年便会增加一倍;而经常被引用的“18个月”…...

四级英语翻译随堂笔记
降维表达:中译英,英译英 没有强调主语,没有说明主语:用被动 但如果实在不行,再增添主语 不会就不翻译,不要乱翻译 以xxx为背景:against the backdrop of the xxx eg:against the backdrop of…...

Nacos支持的配置格式及其在微服务架构中的应用
今天,我想和大家探讨一下Nacos这一重要的微服务组件,特别是它所支持的配置格式以及这些格式在微服务架构中的应用。 一、Nacos简介 Nacos是阿里巴巴开源的一个更易于构建云原生应用的动态服务发现、配置管理和服务管理平台。它提供了服务发现、配置管理…...
-OD统一考试(C卷D卷))
2024年华为OD机试真题-小明找位置-(C++)-OD统一考试(C卷D卷)
题目描述: 小朋友出操,按学号从小到大排成一列;小明来迟了,请你给小明出个主意,让他尽快找到他应该排的位置。 算法复杂度要求不高于nLog(n);学号为整数类型,队列规模<=10000; 输入描述: 1、第一行:输入已排成队列的小朋友的学号(正整数),以”,”隔开; …...
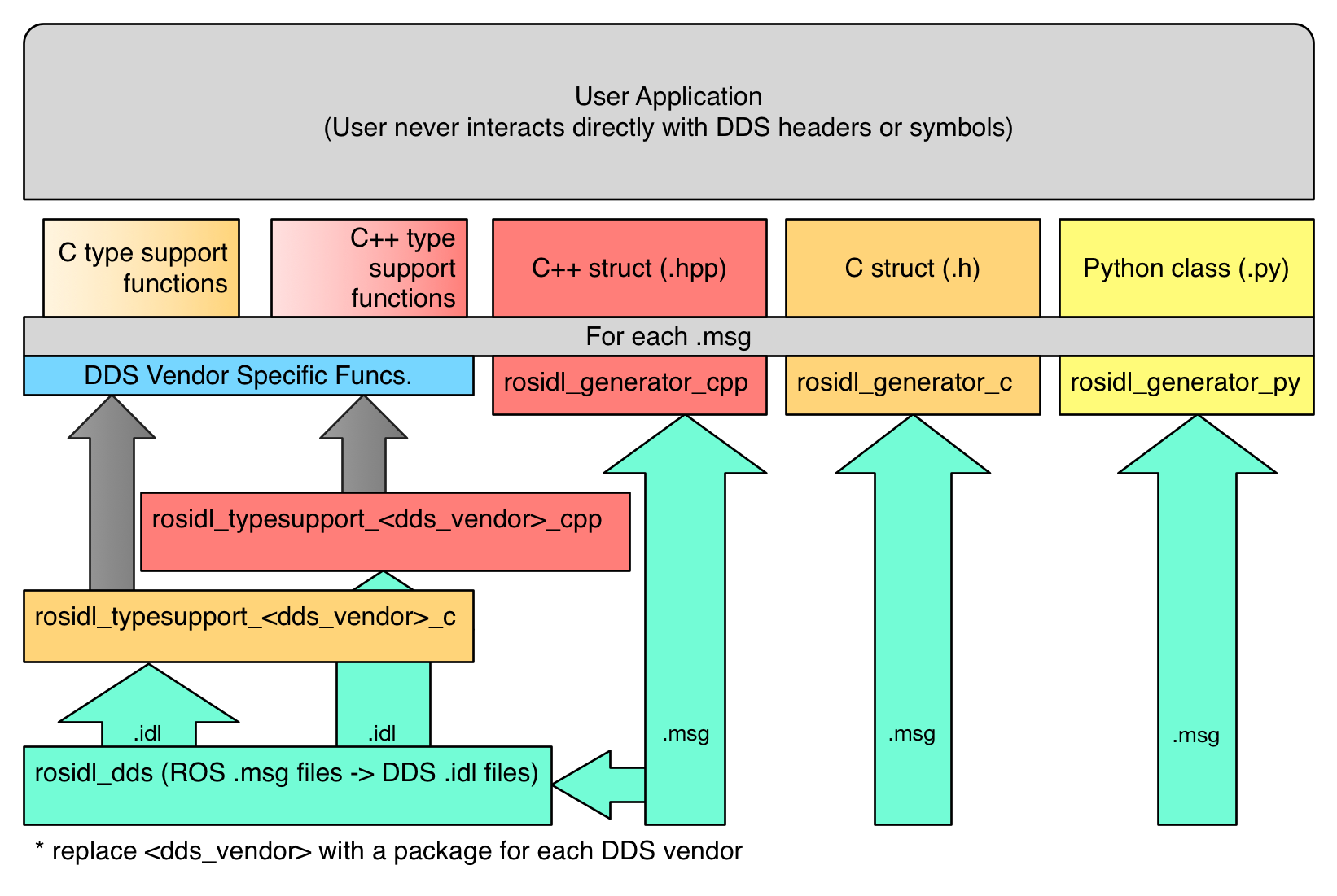
机器人系统ros2内部接口介绍
内部 ROS 接口是公共 C API ,供创建客户端库或添加新的底层中间件的开发人员使用,但不适合典型 ROS 用户使用。 ROS客户端库提供大多数 ROS 用户熟悉的面向用户的API,并且可能采用多种编程语言。 内部API架构概述 内部接口主要有两个&#x…...

跟随Facebook的足迹:社交媒体背后的探索之旅
在当今数字化时代,社交媒体已经成为了人们日常生活中不可或缺的一部分。而在这庞大的社交媒体网络中,Facebook作为其中的巨头,一直在引领着潮流。从创立之初的一个大学社交网络到如今的全球性平台,Facebook的发展历程承载了无数故…...

面试题分享之Java并发篇
注意:文章若有错误的地方,欢迎评论区里面指正 🍭 系列文章目录 面试题分享之Java集合篇(三) 面试题分享之Java集合篇(二) 面试题分享之Java基础篇(三) 前言 今天给小…...

bpmn-js 多实例配置MultiInstanceLoopCharacteristics实现或签会签
使用bpmn-js流程图开发过程中会遇到会签和或签的问题,这个时候我们就需要使用多实例配置来实现BPMN 2.0的配置实现了,多实例任务,是从流程编辑概念之初也就是Activiti时期就存在的一个方式。所谓的多实例任务也就是字面意思,一个任务由多个人完成,常见于我们的审批流程的或…...
【gpedit.msc】组策略编辑器的安装,针对windows家庭版,没有此功能
创建一个记事本文件然后放入以下内容 echo offpushd "%~dp0"dir /b %systemroot%\Windows\servicing\Packages\Microsoft-Windows-GroupPolicy-ClientExtensions-Package~3*.mum >gp.txtdir /b %systemroot%\servicing\Packages\Microsoft-Windows-GroupPolicy-…...
带EXCEL附件邮件发送相关代码
1.查看生成的邮件 2.1 非面向对象的方式(demo直接copy即可) REPORT Z12. DATA: IT_DOCUMENT_DATA TYPE SODOCCHGI1,IT_CONTENT_TEXT TYPE STANDARD TABLE OF SOLISTI1 WITH HEADER LINE,IT_PACKING_LIST TYPE TABLE OF SOPCKLSTI1 WITH HEADER LIN…...

【算法作业】均分卡牌,购买股票
问题描述 John 有两个孩子,在 John病逝后,留下了一组价值不一定相同的魔卡, 现在要求你设计一种策略,帮John的经管人将John的这些遗产分给他的两个孩子,使得他们获得的遗产差异最小(每张魔卡不能分拆&#…...
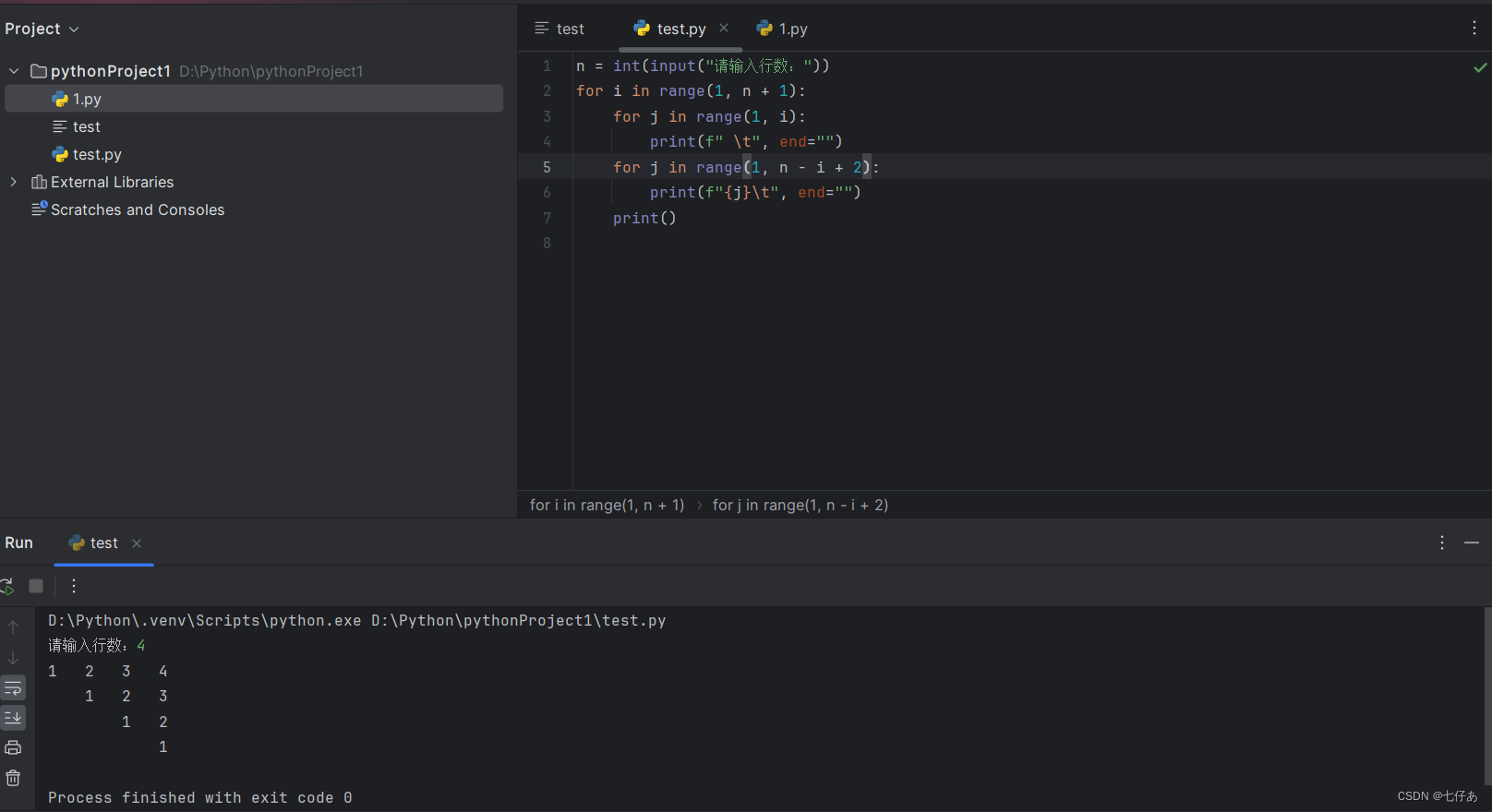
python作业
题目 分析 步骤: 判断先画空格还是数字 当有n层时,第i层有多少个空格第i层的起始数字是几,结尾是几,即数字取值范围当有n层时,第i层有多少个数字 代码 模式A n int(input("请输入行数:")) for i in range(…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...

关于easyexcel动态下拉选问题处理
前些日子突然碰到一个问题,说是客户的导入文件模版想支持部分导入内容的下拉选,于是我就找了easyexcel官网寻找解决方案,并没有找到合适的方案,没办法只能自己动手并分享出来,针对Java生成Excel下拉菜单时因选项过多导…...
)
Leetcode33( 搜索旋转排序数组)
题目表述 整数数组 nums 按升序排列,数组中的值 互不相同 。 在传递给函数之前,nums 在预先未知的某个下标 k(0 < k < nums.length)上进行了 旋转,使数组变为 [nums[k], nums[k1], …, nums[n-1], nums[0], nu…...

从零开始了解数据采集(二十八)——制造业数字孪生
近年来,我国的工业领域正经历一场前所未有的数字化变革,从“双碳目标”到工业互联网平台的推广,国家政策和市场需求共同推动了制造业的升级。在这场变革中,数字孪生技术成为备受关注的关键工具,它不仅让企业“看见”设…...

如何通过git命令查看项目连接的仓库地址?
要通过 Git 命令查看项目连接的仓库地址,您可以使用以下几种方法: 1. 查看所有远程仓库地址 使用 git remote -v 命令,它会显示项目中配置的所有远程仓库及其对应的 URL: git remote -v输出示例: origin https://…...
