【3D目标检测】常见相关指标说明
一、mAP指标
mean Average Precision(平均精度均值),它是目标检测和信息检索等任务中的重要性能指标。mAP 通过综合考虑精度和召回率来衡量模型的总体性能。
1.1 精度(Precision)
表示检索到的目标中实际为正确目标的比例,计算公式为

1.2 召回率(Recall)
表示所有目标中成功被检索到的比例,计算公式为

1.3 平均精度(AP)
-
平均精度表示的是在不同的召回率阈值下,计算模型的平均精度。通常通过绘制 PR 曲线(Precision-Recall 曲线)计算。
-
PR 曲线的横轴为召回率,纵轴为精度。AP 是 PR 曲线下的面积,即对该曲线进行积分的结果。
1.4 mAP的计算
-
mAP 是对多个类别的 AP 求平均得出的数值。
-
如果目标检测任务中包含 N 个类别,则计算每个类别的 AP,并对所有类别的 AP 取平均,即:
1.5 mAP在2D目标检测的计算
在目标检测中,通常设定一个置信度阈值,用于判定检测结果是否被认为是正例(即预测的目标)。常见的阈值有0.5,即 IOU(交并比)≥ 0.5 被视为有效检测。
比如mAP@0.5表示将IoU设为0.5时,计算每一类的所有图片的AP,然后所有类别求平均得到mAP;
mAP@.5:.95表示在不同IoU阈值(从0.5到0.95,步长0.05)(0.5、0.55、0.6、0.65、0.7、0.75、0.8、0.85、0.9、0.95)上的平均mAP。
def ap_per_class(tp, conf, pred_cls, target_cls, eps=1e-16):i = np.argsort(-conf)tp, conf, pred_cls = tp[i], conf[i], pred_cls[i]unique_classes, nt = np.unique(target_cls, return_counts=True)nc = unique_classes.shape[0]ap = np.zeros((nc, tp.shape[1]))p, r = np.zeros((nc, 1000)), np.zeros((nc, 1000))for ci, c in enumerate(unique_classes):i = pred_cls == cn_l = nt[ci]n_p = i.sum()if n_p == 0 or n_l == 0:continuefpc = (1 - tp[i]).cumsum(0)tpc = tp[i].cumsum(0)recall = tpc / (n_l + eps)precision = tpc / (tpc + fpc)for j in range(tp.shape[1]):ap[ci, j], _, _ = compute_ap(recall[:, j], precision[:, j])return ap.mean(0)结合YOLO仓库中的代码进行说明,
np.argsort: 按检测置信度对预测框排序。
unique_classes: 获取数据集中存在的目标类别。
compute_ap 函数:计算PR曲线,并从中得到每个类别的平均精度。通过曲线下面积得到AP,计算上是使用插值方法在固定的召回率点(例如 [0, 0.01, 0.02, ..., 1])计算精度值,并通过梯形法则对这些点进行积分,得到 AP。
def compute_ap(recall, precision):mrec = np.concatenate(([0.0], recall, [1.0]))mpre = np.concatenate(([1.0], precision, [0.0]))mpre = np.flip(np.maximum.accumulate(np.flip(mpre)))method = "interp"if method == "interp":x = np.linspace(0, 1, 101)ap = np.trapz(np.interp(x, mrec, mpre), x)else:i = np.where(mrec[1:] != mrec[:-1])[0]ap = np.sum((mrec[i + 1] - mrec[i]) * mpre[i + 1])return ap, mpre, mrec输入参数:recall: 一个列表或数组,表示不同阈值下的召回率值。precision: 一个列表或数组,表示不同阈值下的精确度值。
输出值:返回三个值:平均精确度(AP),处理过的精确度曲线,以及处理过的召回率曲线。
选择一种计算PR曲线下面积的方法,函数中提供了两种方法:
-
interp:使用插值方法,在 [0, 1] 范围内将召回率分为 101 个点,然后使用 np.interp 进行插值计算,并通过 np.trapz 计算面积,这是COCO 评价标准下的插值方法。
-
continuous:直接根据召回率变化的点计算面积。
说明一下这里的细节:
-
翻转精确度曲线: 使用 np.flip 将精确度曲线倒置。假设原始精确度数组是 [0.5, 0.6, 0.4, 0.7],翻转后为 [0.7, 0.4, 0.6, 0.5]。
-
计算累积最大值: 倒置后的精确度数组作为输入,传递给 np.maximum.accumulate 计算累积最大值。该函数在遍历输入数组时,将输出元素设置为从当前索引开始到数组末尾范围内的最大值。np.maximum.accumulate 的计算结果是 [0.7, 0.7, 0.7, 0.7],确保所有值都大于或等于前一个值。
-
翻转回原始顺序: 最后再使用 np.flip 将累积最大值的数组翻转回原始顺序,得到 [0.7, 0.7, 0.7, 0.7],这样得到的曲线就是非递减的包络线。在现实情况下,精确度曲线有时可能会因为某个特定的召回率阈值而出现波动,使得曲线有时会上升,有时会下降。然而,在计算PR曲线下面积时,为了使结果更具稳定性和准确性,需要将这些下降的部分“填平”以形成一个包络线,确保整个曲线是平滑和非递减的。
1.6 mAP在3D目标检测的计算
在3D目标检测任务中,为了顾及小目标物体,不再适用2D中基于IoU的mAP计算方式,而是计算框在BEV视图下的2D中心点之间的欧氏距离。
设置一个阈值(如2米),如果预测框和真实框的中心点距离小于这个阈值,则认为这两个框匹配。
这种方法特别有利于提高小物体的匹配率。在3D环境中,小物体的IoU可能由于深度和遮挡问题而较难计算或得到较低的匹配度。使用中心点距离作为匹配标准简化了匹配过程,使得评估对于各种尺寸的物体都更为公平。
通过BEV的2D中心距离d来计算。这样解耦了物体的尺寸和方向对AP计算的影响。d设置为{0.5,1,2,4}米。在计算AP时,去除了低于10%的recall和precision并用0来代替这些区域(所以这里的PR曲线表示10%以上的召回率和精度,以降低噪声影响)。不同类C以及不同距离难度D用来计算mAP。
二、NDS
2.1 mATE(Average Translation Error)
平均平移误差(ATE)衡量的是预测的物体中心点与真实物体中心点之间的平均欧几里得距离,单位为米。
2.2 mASE(Average Scale Error)
平均尺度误差(ASE)衡量的是预测的物体尺寸与真实物体尺寸之间的一致性,通过计算1减去角度对齐后的三维交并比(IoU)。
2.3 mAOE(Average Orientation Error)
平均角度误差(AOE)衡量的是预测物体方向与真实物体方向之间的最小偏航角差异。所有角度均在整个360度周期内测量,但障碍物除外,它们是在180度周期内测量的。
2.4 mAVE(Average Velocity Error)
平均速度误差(AVE)是预测物体速度与真实物体速度之间的二维L2范数差(m/s)。
其中 vx 和 vy 表示速度在x轴和y轴上的分量。
2.5 mAAE(Average Attribute Error)
平均属性错误(AAE)被定义为类别分类的错误率,即1减去分类准确度。
其中 acc 是分类的准确度,即正确分类的样本数占总样本数的比例。
2.6 NDS计算
上述指标称为True Positive 指标。所有TP指标都是在匹配时使用 d=2 米中心距计算的,并且都被设计为正标量。如果特定类别未实现10%以上召回率,则该类别的所有 TP 错误都将设置为1。同时,忽略了一些类别的测量。
-
AVE(平均速度误差):不适用于路标锥和障碍物,因为它们是固定不动的,没有速度可测量。
-
AOE(平均角度误差):不适用于路标锥,因为它们没有明确的方向或朝向,无法评估其角度误差。
-
AAE(平均属性误差):不适用于路标锥和障碍物,因为这些类别没有定义明确的属性,无法计算属性相关的错误率。
NDS 的一半基于检测性能,而另一半则根据框位置、大小、方向、属性和速度来量化检测质量。由于 mAVE、mAOE 和 mATE 可能大于 1 ,因此会将每个指标限制在 0 和 1 之间。
相关文章:
【3D目标检测】常见相关指标说明
一、mAP指标 mean Average Precision(平均精度均值),它是目标检测和信息检索等任务中的重要性能指标。mAP 通过综合考虑精度和召回率来衡量模型的总体性能。 1.1 精度(Precision) 表示检索到的目标中实际为正确目标…...

QT设计模式:工厂模式
基本概念 工厂模式是一种创建型设计模式,用于将对象的创建逻辑与使用者分离,以实现对象的创建和使用的解耦。工厂模式提供了一个统一的接口来创建对象,而客户端代码只需通过该接口来请求所需的对象,而不需要知道具体的对象创建细…...

【电路笔记】-容抗
容抗 文章目录 容抗1、概述2、容抗示例13、容抗示例 24、容抗示例 35、分压器修订6、总结1、概述 容抗是电容器的复阻抗,其值随应用频率而变化。 与不依赖于频率的电阻不同,在交流电路中,电抗受电源频率的影响,并且其行为方式与电阻类似,两者都以欧姆为单位测量。 电抗会…...

基于若依框架搭建网站的开发日志(一):若依框架搭建、启动、部署
RuoYi(基于SpringBoot开发的轻量级Java快速开发框架) 链接:开源地址 若依是一款开源的基于VueSpringCloud的微服务后台管理系统(也有SpringBoot版本),集成了用户管理、权限管理、定时任务、前端表单生成等…...

Android中Fragment失去焦点的场景
在Android开发中,Fragment的生命周期方法onPause()会在以下几种情况下被调用: 当Fragment所在的Activity开始与其他Activity进行交互时,例如按下Home键或其他Activity获得焦点,导致当前Activity失去焦点,从而使得所有关…...

Linux变量的认识及环境变量配置详解
文章目录 1、变量的划分2、局部变量3、全局变量4、环境变量4.1、概述4.2、配置临时环境变量4.3、配置永久环境变量4.3.1、用户级配置文件1)配置方法一:~/.bashrc文件2)配置方法二:~/.profile文件3)配置方法三ÿ…...
【excel】数据非数值导致排序失效
场景 存在待排序列的数值列,但排序失效,提示类型有问题: 解决 选中该列,数据→分列 而后发现提示消失,识别为数字,可正常排序。...

软件网关--Nginx
Nginx 的多功能用途 Nginx 是构建现代化分布式应用程序的重要工具,它的功能远不止于高性能的 Web 服务器和反向代理。它还能充当 API 网关,处理前后端通信、认证、授权、监控等任务。以下是 Nginx 的主要用途: 前后端通信代理:N…...
sourceTree push失败
新电脑选择commit and push,报错了,不过commit成功,只不过push失败了。 原因是这个,PuTTYs cache and carry on connecting. 这里的ssh选择的是 PuTTY/Plink,本地没有这个ssh密钥,改换成openSSHÿ…...

leetCode33. 搜索旋转排序数组
leetCode33. 搜索旋转排序数组 题目思路 此题的特点是:排好序循环的数组:特点:可以分为两个区间,一半升序,一半降序,或者全部升序 我们可以用二分法,找出升序 到降序的那个临界值,并…...

JS_监听dom变化触发,new MutationObserver
MutationObserver 是一个用于监测 DOM 变化的接口,它提供了一种机制来异步观察在特定元素或文档中发生的 DOM 变化。 MutationObserver 的作用包括: 1.监测 DOM 变化:你可以创建一个 MutationObserver 实例,并指定一个回调函数。…...

什么是驱动数字签名?如何获取驱动数字签名?
Windows 驱动程序承载着计算机实现的各种内核和用户模式功能。如果驱动程序被黑客攻击,可能会产生很多问题。Windows通过数字签名来验证驱动程序包的完整性及发布者的身份。2020年10月的安全更新中,微软加强了对驱动软件的验证,如果Windows无…...

【leetcode】优先队列题目总结
优先队列的底层是最大堆或最小堆 priority_queue<Type, Container, Functional>; Type是要存放的数据类型Container是实现底层堆的容器,必须是数组实现的容器,如vector、dequeFunctional是比较方式/比较函数/优先级 priority_queue<Type>…...

typescript 中的泛型
泛型:解决 类、接口、方法的复用性、以及对不特定数据类型的支持 传入的参数与返回参数类型一致 泛型函数 // T表示泛型,具体什么类型是调用这个方法的时候决定的 function getData<T>(value: T): T {return value } getData<number>(123) …...
:列主元消元法解线性方程组)
计算方法实验2(补充):列主元消元法解线性方程组
C源代码 #include<bits/stdc.h> using namespace std;// 列主元消去法求解线性方程组 vector<long double> Column_Elimination(vector<vector<long double>> A, vector<long double> b);int main() {vector<vector<long double>> …...

Qt扫盲-Qt D-Bus概述
Qt D-Bus概述 一、概述二、总线三、相关概念1. 消息2. 服务名称3. 对象的路径4. 接口5. 备忘单 四、调试五、使用Qt D-Bus 适配器1. 在 D-Bus 适配器中声明槽函数1. 异步槽2. 只输入槽3. 输入输出槽4. 自动回复5. 延迟回复 一、概述 D-Bus是一种进程间通信(IPC)和远程过程调用…...
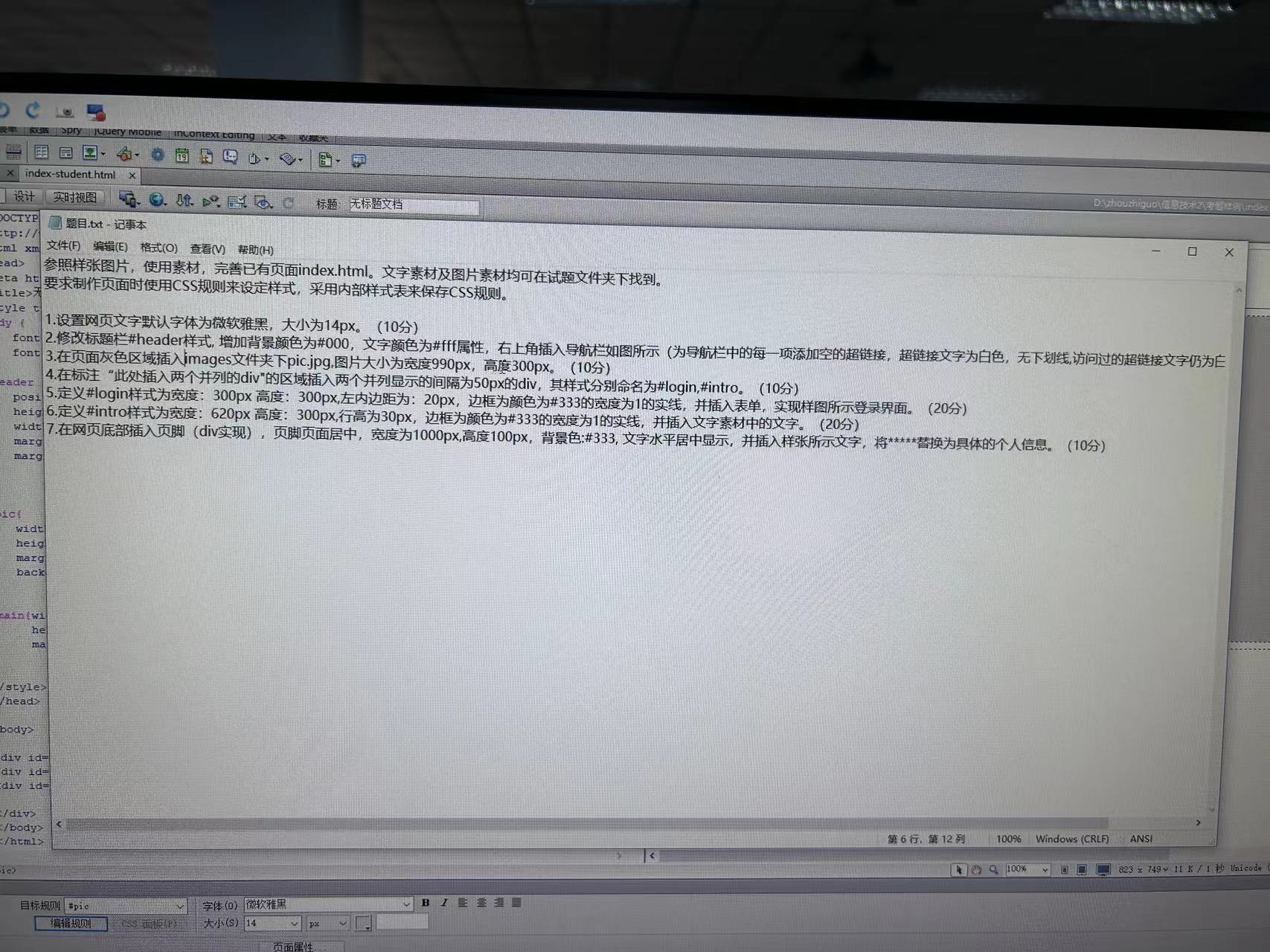
懒洋洋作业讲解
懒洋洋作业讲解 环境配置 1.软件下载:DCloud - HBuilder、HBuilderX、uni-app、uniapp、5、5plus、mui、wap2app、流应用、HTML5、小程序开发、跨平台App、多端框架 2.软件介绍 HBuilder是由DCloud(数字天堂)推出的一款面向HTML5的Web开发…...
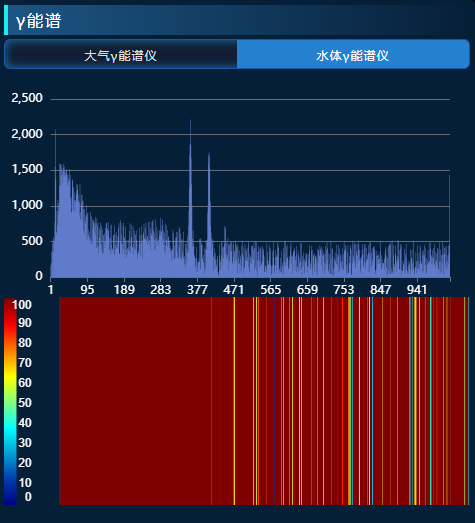
vue3 + ts实现canvas绘制的waterfall
实际运行效果(仅包含waterfall图表部分) component.vue <template><div ref"heatmap" :style"{ height: props.containerHeight px }" /> </template><script setup> import ColorMap from "color…...

代码随想录算法训练营第四十四天
sad的一天,明天开始上班,而且娃还行,媳妇儿状态不稳定,太难了也!!! 完全背包 #include<vector> #include<iostream> using namespace::std; int main(){int N;//种类int V;//空间ci…...

【3dmax笔记】027:配置修改器集、工具栏自定义与加载
文章目录 一、配置修改器集二、自定义工具栏三、加载工具栏 一、配置修改器集 可以把自己常用的修改命令放到右边框中的部分,便于自己的操作,省去了每次都要花半天时间找命令的尴尬。新建一个二维或者三维物体,点击修改面板,点击…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

#Uniapp篇:chrome调试unapp适配
chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器:Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...

云原生安全实战:API网关Kong的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关(API Gateway) API网关是微服务架构中的核心组件,负责统一管理所有API的流量入口。它像一座…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...
