互相关延时估计 Matlab仿真
文章目录
- 互相关延时估计
- 什么是互相关延时估计?
- 原理
- 代码实现
- 总结
互相关延时估计
互相关延时估计是一种信号处理技术,用于计算两个信号之间的时间延迟。在本篇博客中,我们将使用MATLAB来实现互相关延时估计,并提供多个例子和代码,以帮助更好地理解该技术。
什么是互相关延时估计?
互相关延时估计是通过比较两个信号的相似性来计算它们之间的时间延迟。在信号处理中,时间延迟是指一个信号相对于另一个信号的延迟时间。互相关延时估计在许多领域中都有广泛应用,包括语音识别、音频处理、图像处理等。
原理
当计算互相关函数时,可以将其中一个信号向右移动kkk个样本,然后将该信号与另一个信号的每个样本相乘并求和。最后,将计算的结果作为互相关函数的值。
举一个简单的例子来说明如何计算互相关函数。假设我们有两个信号 x={1,2,3}x = \{1, 2, 3\}x={1,2,3} 和 y={2,1,1}y = \{2, 1, 1\}y={2,1,1}。我们想要计算这两个信号之间的互相关函数。根据互相关函数的定义,我们可以得到:
Rxy(k)=∑n=−∞∞x(n)y(n−k)R_{xy}(k) = \sum_{n=-\infty}^{\infty}x(n)y(n-k)Rxy(k)=n=−∞∑∞x(n)y(n−k)
我们可以通过手动计算互相关函数来理解它的计算过程。具体来说,我们可以将信号 xxx 向右移动 kkk 个样本,然后将其与信号 yyy 的每个样本相乘并求和。在这个例子中,我们手动计算得到这两个信号之间的互相关函数为 Rxy={7,3,1,0,0}R_{xy} = \{7, 3, 1, 0, 0\}Rxy={7,3,1,0,0}。其中,Rxy(0)R_{xy}(0)Rxy(0) 是互相关函数的最大值,对应于两个信号之间的最佳延迟。
在信号处理中,我们经常需要将两个信号进行比较。但是,由于信号可能会出现时间偏移,因此需要将信号进行时间同步,以便进行比较。这个时间偏移就是我们这里所说的延迟。延迟是指一个信号相对于另一个信号的时间偏移量。
在Matlab中,可以使用内置的xcorr函数来计算互相关函数。对于这个例子,我们可以使用以下代码计算互相关函数:
x = [1, 2, 3];
y = [2, 1, 1];
[corr, lag] = xcorr(x, y);
最后,corr向量中的最大值对应于延迟0,即两个信号之间没有延迟。而在这个例子中,我们手动计算得到的最大值是在延迟0的位置,与Matlab计算的结果相符。
因此,使用互相关函数进行延时估计可以帮助我们在信号处理中对信号进行时间同步,以便进一步处理。
代码实现
以下是一个简单的Matlab代码,用于计算两个信号之间的延迟:
% 生成两个信号
fs = 1000; % 采样频率
t = 0:1/fs:1; % 时间向量
x = sin(2*pi*50*t); % 50 Hz正弦波
y = sin(2*pi*50*t + pi/2); % 相位差为90度的50 Hz正弦波% 计算互相关函数
[corr, lag] = xcorr(x, y);% 找到延迟
[~,I] = max(abs(corr));
delay = lag(I);
delay_time = delay/fs; % 延迟时间% 显示结果
fprintf('Delay between x and y is %f seconds.', delay_time);% 绘制互相关函数图像
figure;
subplot(2,1,1);
plot(t, x, 'b', t, y, 'r');
xlabel('Time (s)');
ylabel('Amplitude');
title('Original Signals');
legend('Signal x', 'Signal y');subplot(2,1,2);
plot(lag, corr);
xlabel('Lag');
ylabel('Correlation');
title('Cross-Correlation of x and y');运行结果:Delay between x and y is 0.005000 seconds.
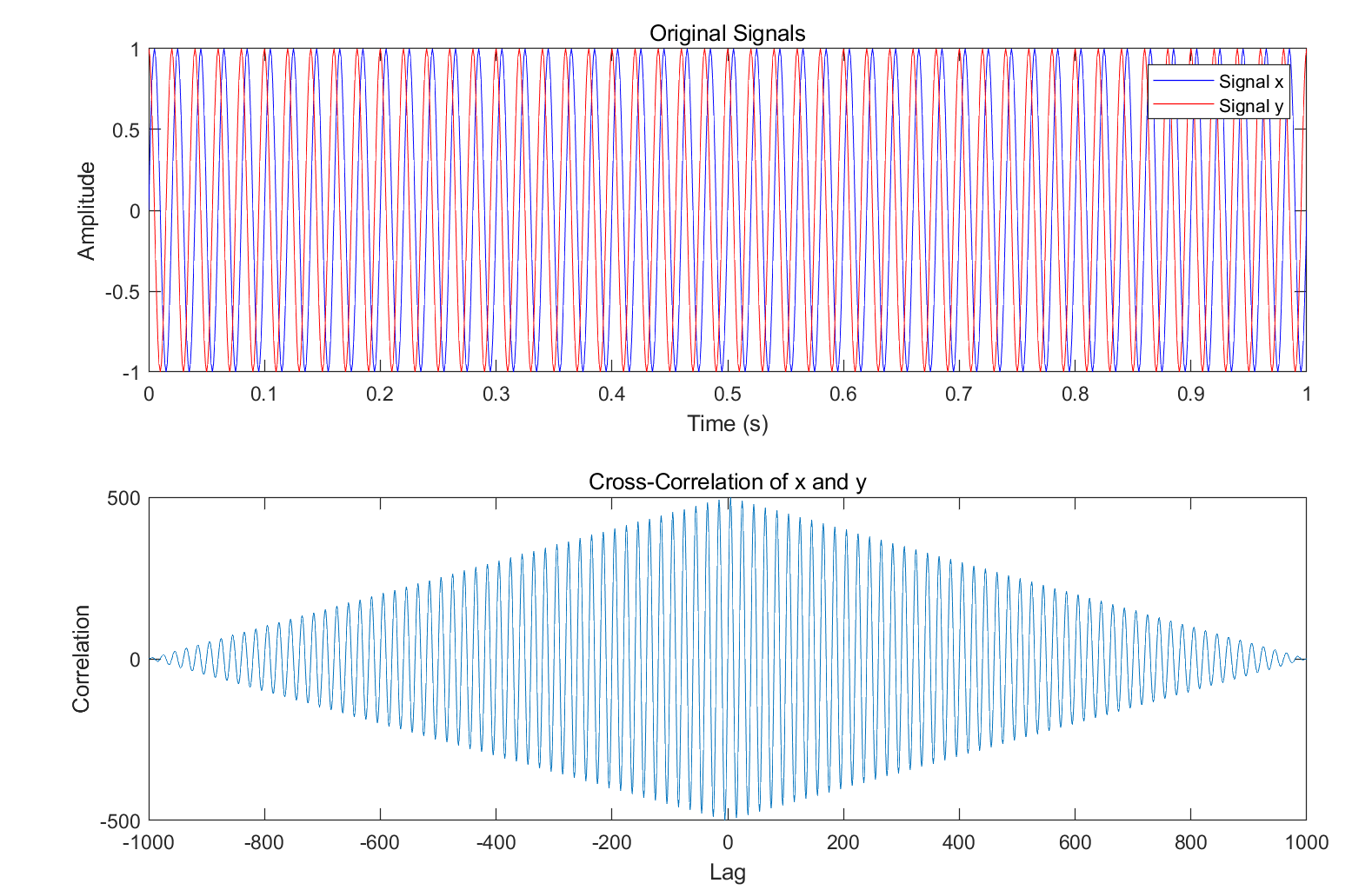
在上面的代码中,我们生成了两个相位差为90度的50Hz正弦波。然后我们使用xcorr函数计算它们之间的互相关函数。xcorr函数返回两个参数:corr和lag。corr是互相关函数的值,lag是所有延迟值的向量。我们使用max函数找到互相关函数的峰值,并使用lag找到对应的延迟。为了得到实际延迟时间,我们将延迟样本数除以采样频率。
互相关函数的计算原理是:将一个信号延迟kkk个样本,然后将其与另一个信号的每个样本相乘并求和。这个过程在式子Rxy(k)=∑n=−∞∞x(n)y(n−k)R_{xy}(k) = \sum_{n=-\infty}^{\infty}x(n)y(n-k)Rxy(k)=∑n=−∞∞x(n)y(n−k)中表示。互相关函数的最大值对应于两个信号之间的最佳延迟。因此,我们可以使用互相关函数来估计两个信号之间的时间延迟。
除了上面的代码,我们还可以使用以下代码生成两个矩形波,并计算它们之间的延迟:
% 生成两个信号
fs = 1000; % 采样频率
t = 0:1/fs:1; % 时间向量
x = square(2*pi*50*t); % 50 Hz矩形波
y = square(2*pi*50*t + pi/2); % 相位差为90度的50 Hz矩形波% 计算互相关函数
[corr, lag] = xcorr(x, y);% 找到延迟
[~,I] = max(abs(corr));
delay = lag(I);
delay_time = delay/fs; % 延迟时间% 显示结果
fprintf('Delay between x and y is %f seconds.', delay_time);% 绘制互相关函数图像
figure;
plot(lag, corr);
xlabel('Lag');
ylabel('Correlation');
title('Cross-Correlation of x and y');
运行结果:Delay between x and y is 0.005000 seconds.
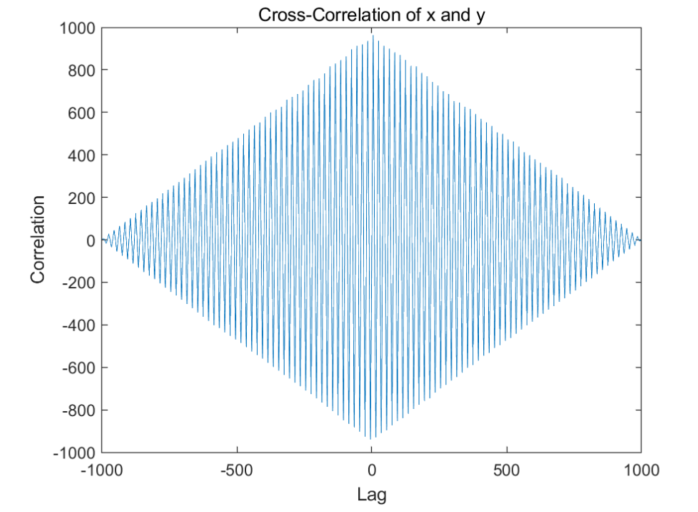
在上面的代码中,我们生成了两个相位差为90度的50Hz矩形波。然后我们使用xcorr函数计算它们之间的互相关函数。最后,我们找到互相关函数的峰值,并计算其对应的延迟。将延迟样本数除以采样频率,可以得到延迟时间。
此外,我们还可以使用以下代码生成两个噪声信号,并计算它们之间的延迟:
% 生成两个信号
fs = 1000; % 采样频率
t = 0:1/fs:1; % 时间向量
x = randn(size(t)); % 高斯白噪声
y = circshift(x, 100); % 将x向右移动100个样本% 计算互相关函数
[corr, lag] = xcorr(x, y);% 找到延迟
[~,I] = max(abs(corr));
delay = lag(I);
delay_time = delay/fs; % 延迟时间% 显示结果
fprintf('Delay between x and y is %f seconds.', delay_time);% 绘制互相关函数图像
figure;
plot(lag, corr);
xlabel('Lag');
ylabel('Correlation');
title('Cross-Correlation of x and y');
输出结果Delay between x and y is -0.100000 seconds.
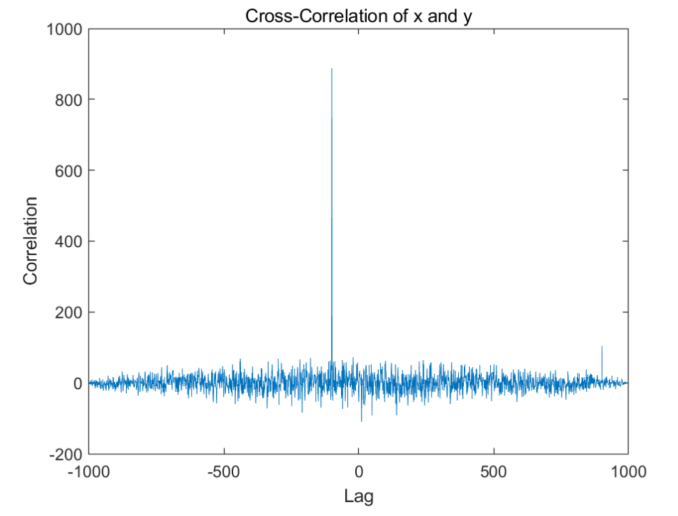
在上面的代码中,我们生成了两个高斯白噪声信号。然后我们将其中一个信号向右移动了100个样本,并使用xcorr函数计算了它们之间的互相关函数。最后,我们找到互相关函数的峰值,并计算其对应的延迟。将延迟样本数除以采样频率,可以得到延迟时间。
总结
本教程介绍了如何使用互相关函数进行延时估计。我们使用Matlab进行了代码实现和仿真。通过本教程,我们希望读者了解互相关函数的原理和应用,并能够使用Matlab实现延时估计。
相关文章:

互相关延时估计 Matlab仿真
文章目录互相关延时估计什么是互相关延时估计?原理代码实现总结互相关延时估计 互相关延时估计是一种信号处理技术,用于计算两个信号之间的时间延迟。在本篇博客中,我们将使用MATLAB来实现互相关延时估计,并提供多个例子和代码&a…...
谷歌插件Fetch在不同页面之间Cookie携带情况详解
content script 和 script inject 表现情况 在碰到content script 注入和用script标签注入一样,即使服务端有写入Cookie到域名下在该tab标签应用下也不会被保存,所以在发送时也无法自动携带,所以通过content script和<script>这种方式…...
)
Vue学习笔记(8)
8.1 组件自定义事件 在 Vue 中,组件可以通过自定义事件来实现组件之间的通信。自定义事件可以让一个组件触发一个事件,并向其他组件传递数据。以下是自定义事件的实现步骤: 在组件中定义一个事件名:可以在组件中使用 $emit 方法来…...
知道一个服务器IP应该怎么进入
首先我是国内,访问国外的网站比如谷歌等,访问特别慢,有时候甚至登录不进去。现在知道了一个台湾或者国外的服务器应该怎么登录进去呢?知道服务器IP之后,你还需要知道服务器的远程端口帐号密码才能登录的。知道上面信息…...

【计算机基础】Socket IO
一、I/O 模型 一个输入操作通常包括两个阶段: 等待数据准备好从内核向进程复制数据 对于一个套接字上的输入操作,第一步通常涉及等待数据从网络中到达。当所等待数据到达时,它被复制到内核中的某个缓冲区。第二步就是把数据从内核缓冲区复…...
mingw编译opencv
我这里是msys2 这个是msys2的教程 https://blog.csdn.net/qq_39942341/article/details/105931335?ops_request_misc%257B%2522request%255Fid%2522%253A%2522167821146216800197067008%2522%252C%2522scm%2522%253A%252220140713.130102334.pc%255Fblog.%2522%257D&requ…...
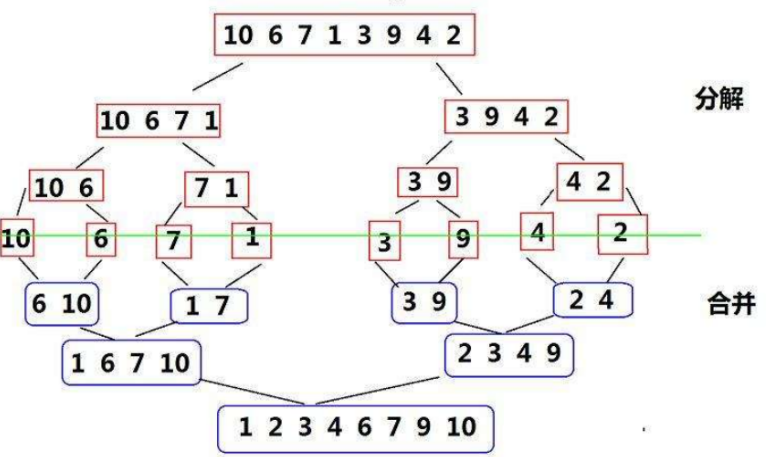
数据结构(八)排序
一、排序的概念以及引用概念排序:所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。稳定性:假定在待排序的记录序列中,存在多个具有相同的关键字的记录,…...

函数习题:用函数实现判断一个整数是否能被n整除
Description 输入一组整数,输入0结束(这组整数不包含0),输出其中能被n整除的所有整数之和(n为整数,不用考虑n为0的情况), n及这组整数均由键盘输入。首先输入n,再输入一…...

SAP 创建会计冲销凭证
“功能描述:根据传输过来数据创建会计冲销凭证,并返回消息和状态 *”---------------------------------------------------------------------- "“本地接口: *” IMPORTING *" VALUE(IW_ZTFKCX0010) TYPE ZTFKCX0010 *" EXP…...
Jetson(Ubuntu18.04)设备无法ping通百度能ping通局域网错误集合,(神奇的是这样的情况下Todesk等远程确没有问题)
一、.打开DNS,意思是取消注释添加114.114.114.114 ,文件如下 vim /etc/systemd/resolved.conf [Resolve] #DNS #FallbackDNS #Domains #LLMNRno #MulticastDNSno #DNSSECno #Cacheyes #DNSStubListeneryes然后重启服务sudo systemctl restart systemd-resolved.se…...

Spring的@Conditional注解
前言Conditional是Spring4新提供的注解,它的作用是按照一定的条件进行判断,满足条件给容器注册bean。Conditional的源码定义://此注解可以标注在类和方法上 Target({ElementType.TYPE, ElementType.METHOD}) Retention(RetentionPolicy.RUNTI…...

剑指 Offer 67 把字符串转换成整数
摘要 面试题67. 把字符串转换成整数 一、字符串解析 根据题意,有以下四种字符需要考虑: 首部空格: 删除之即可;符号位:三种情况,即 , − , 无符号";新建一个变量保存符号位࿰…...

【教学典型案例】18.开门小例子理解面向对象
目录一:背景介绍业务场景:业务分析:二:实现思路1、面向过程:2、面向对象(抽象、封装、继承、多态)3、面向对象(抽象、封装、继承、多态、反射)三:实现过程1、…...

Linux环境ENV的概念
一、基本概念 环境变量的含义:程序(操作系统命令和应用程序)的执行都需要运行环境,这个环境是由多个环境变量组成的。 按变量的周期划为永久变量和临时性变量2种: 永久变量:通过修改配置文件,…...

AcWing数据结构 - 数据结构在算法比赛中的应用(下)
目录 Trie树 Trie字符串统计 最大异或对 并查集 合并集合 连通块中点的数量 食物链 堆 堆排序 模拟堆 哈希表 模拟散列表 字符串哈希 Trie树 Trie字符串统计 思路: 设 idx索引用于构建树, 结点son[节点位置][节点分支指针],cnt[]记录单…...
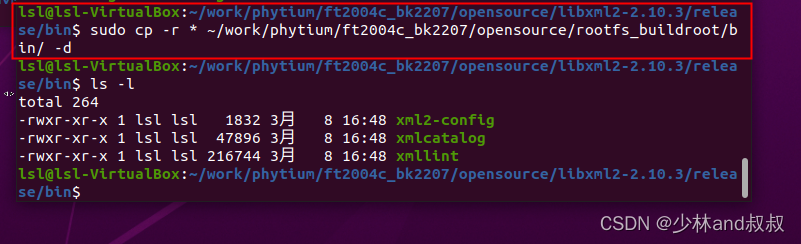
基于嵌入式libxml2的ARM64平台的移植(aarch64)
由于libxml在移植过程中依赖于zlib的库文件,因此本节内容包含zlib(V1.2.13)的移植libxml2(V2.10.3)的移植两部分组成。 (一)zlib的移植(基于arm64) 1、在github上下载zlib的最新源码压缩包&am…...
)
8. 字符串转换整数 (atoi)
题目描述 给你一个 32 位的有符号整数 x ,返回将 x 中的数字部分反转后的结果。 如果反转后整数超过 32 位的有符号整数的范围 [−231, 231 − 1] ,就返回 0。 假设环境不允许存储 64 位整数(有符号或无符号)。 示例 1&#x…...
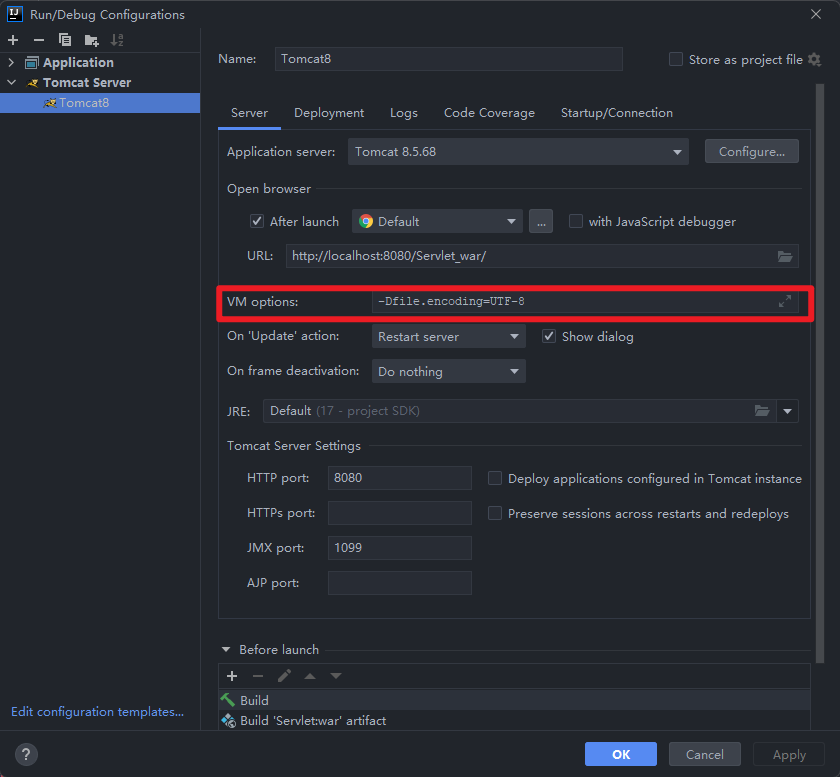
[Tomcat]解决IDEA中的Tomcat中文乱码问题
目录 1、IDEA 2、VM options 3、IDEA启动程序的存放目录 4、Tomcat 写在前面:此方法亲测有效!!! 1、IDEA 2、VM options 加上这两行: -Dfile.encodingUTF-8 -Dconsole.encodingUTF-8 3、IDEA启动程序的存放目录…...

python之dataclasses
一、场景 dataclasses模块提供了一种方便的方法来创建和管理数据对象 它可以帮助开发者更容易地创建简单的类,同时提供了一些实用的功能,例如自动实现__init__()、repr()、eq()等方法。 数据容器:如果您需要一个简单的类来存储一些数据&…...

【MapGIS精品教程】007:MapGIS投影变换案例教程
MapGIS投影变换,包括创建坐标系、定义投影、单点投影、类投影、批量投影。 文章目录 一、创建坐标系1. 创建高斯平面坐标系2. 创建阿尔伯斯投影二、定义投影三、投影变换1. 单点投影2. 类投影3. 批量投影一、创建坐标系 在MagGIS数据库中,有个空间参考系的文件夹,内置了常见…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...
