【机器学习300问】83、深度学习模型在进行学习时梯度下降算法会面临哪些局部最优问题?
梯度下降算法是一种常用的优化方法,用于最小化损失函数以训练模型。然而,在使用梯度下降算法时,可能会面临以下局部最优问题。
(一)非凸函数的局部极小值
问题描述:在复杂的损失函数中,如果目标函数是非凸函数,即存在多个局部最小值点,那么梯度下降有可能会在到达某个局部最小值后停止,而非全局最小值。这意味着找到的解决方案可能不是最优的。
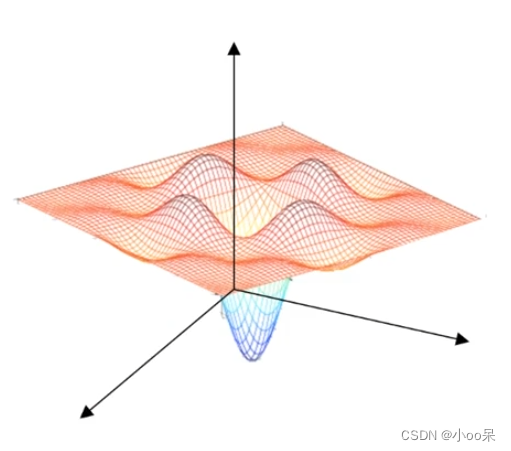
解决思路:
- 增加随机性:通过引入随机性,例如使用随机初始化、随机梯度下降等方法,可以帮助模型跳出局部最小值,并有机会找到更优的解。
- 尝试不同初始值:进行多次训练,使用不同的初始点或不同的参数设置,以增加找到全局最小值的机会。
- 调整学习率:适当调整学习率的大小,使其能够更好地适应不同区域的变化,从而有机会跳出局部最小值。
- 使用动量法:动量法可以帮助模型在参数空间中更好地探索,有助于跳出局部最小值。
(二)鞍点问题
问题描述:在高维空间中,函数可能包含许多鞍点,这些点在某些方向上是局部最小值,在其他方向上是局部最大值。损失函数的梯度可能接近零,尽管当前位置不是极小值。这被称为鞍点。梯度下降在鞍点附近可能会非常缓慢地收敛,或者停滞不前,需要很长时间才能逃离这个区域。因为它同时感受到了下降和上升的方向。

解决思路:
- 增加动量:动量法可以帮助模型在参数空间中更好地探索,有助于跳过鞍点区域。
- 使用自适应学习率算法:如AdaGrad、RMSprop等,它们可以自适应地调整学习率,有助于模型逃离鞍点区域。
- 使用二阶优化算法:考虑使用二阶优化算法,如牛顿法、拟牛顿法等,它们利用二阶导数信息来指导搜索方向,有助于更好地处理鞍点问题。
(三)平台区域
问题描述:损失函数可能存在一些平坦的区域,其中梯度几乎为零。在这些区域内,梯度下降算法的学习速度会显著减慢,因为它依赖于梯度来指导搜索方向。梯度变化太微小,导致模型学习速度缓慢,很难快速逃离这些区域。
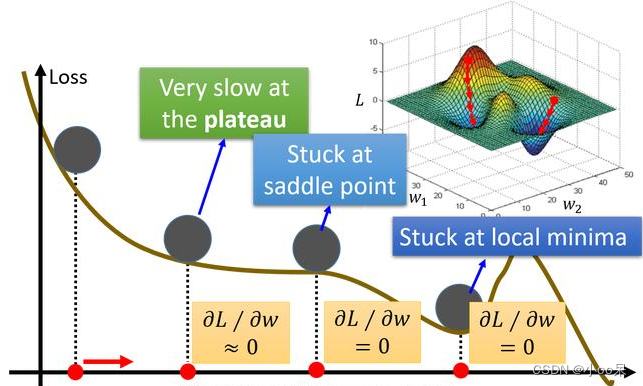
解决思路:
- 增加动量:动量法可以帮助模型在参数空间中更好地探索,有助于快速逃离平台区域。
- 使用自适应学习率算法:如AdaGrad、RMSProp等,它们可以自适应地调整学习率,有助于模型逃离平台区域。
- 进行正则化:添加正则化项有助于引导算法绕过平坦区,寻找到具有更好泛化能力的解。
- 调整学习率:适当调整学习率的大小,使其能够更好地适应不同区域的变化,从而有机会快速逃离平台区域。
相关文章:

【机器学习300问】83、深度学习模型在进行学习时梯度下降算法会面临哪些局部最优问题?
梯度下降算法是一种常用的优化方法,用于最小化损失函数以训练模型。然而,在使用梯度下降算法时,可能会面临以下局部最优问题。 (一)非凸函数的局部极小值 问题描述:在复杂的损失函数中,如果目…...

基于springboot的校园管理系统源码数据库
基于springboot的校园管理系统源码数据库 随着科学技术的飞速发展,社会的方方面面、各行各业都在努力与现代的先进技术接轨,通过科技手段来提高自身的优势,校园管理系统当然也不能排除在外。校园管理系统是以实际运用为开发背景,…...
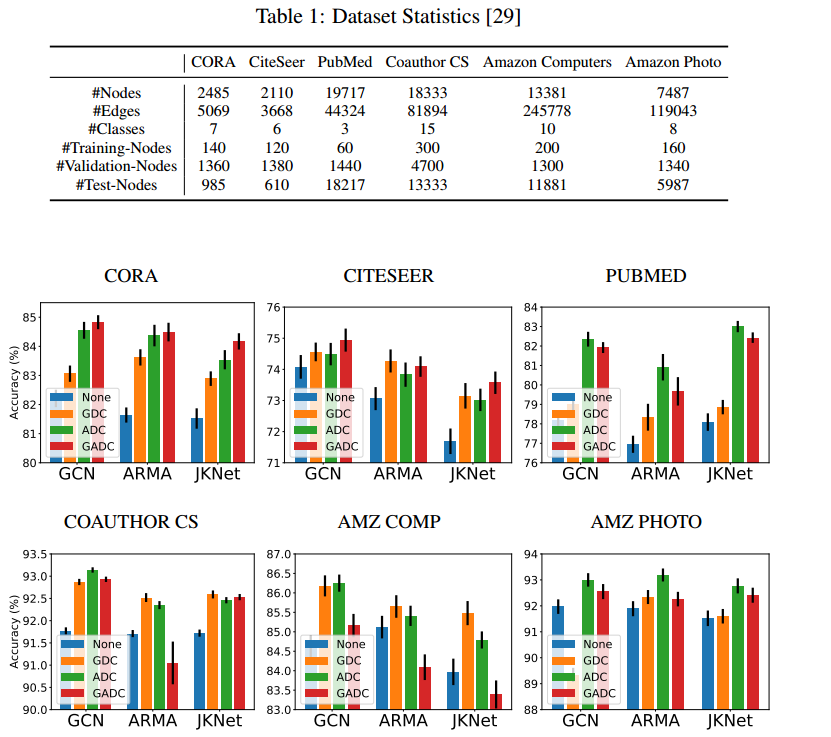
图形网络的自适应扩散 笔记
1 Title Adaptive Diffusion in Graph Neural Networks(Jialin Zhao、Yuxiao Dong、Ming Ding、Evgeny Kharlamov、Jie Tang)【NIPS 2021】 2 Conclusion The neighborhood size in GDC is manually tuned for each graph by conductin…...

vue基础配置
vite.config.ts import { defineConfig } from vite import vue from vitejs/plugin-vue import path from "path"; //引入svg需要用到的插件 import { createSvgIconsPlugin } from vite-plugin-svg-icons //mock插件提供方法 import { viteMockServe } from vite-…...
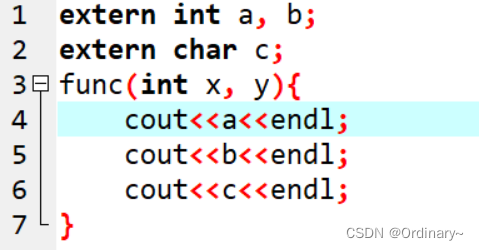
C++基础中的存储类别
存储的类别是变量的属性之一,C语言定义了4种变量的存储类别,分别是auto变量、static变量、register变量和extern变量。以下重点介绍这几种类型。 一、auto变量 auto变量是C默认的存储类型。函数内未加存储类型说明的变量均被称为自动变量,即…...
【NPM】Nginx Proxy Manager 一键申请 SSL 证书,自动续期,解决阿里云SSL免费证书每3个月失效问题
文章目录 1、NPM 简介2、实战Step 1:环境搭建 也可以看作者安装笔记 Step 2:创建容器 2.1 在系统任意位置创建一个文件夹,此文档以~/nginx-proxy-manager为例。2.2 创建docker-compose.yaml2.3 启动NPM服务 Step 3:配置反向代理3…...
教你解决PUBG绝地求生游戏中闪退掉线无法重连回去的问题
《绝地求生》(PUBG),作为一款在全球范围内掀起热潮的战术竞技游戏,以其栩栩如生的战场环境和令人心跳加速的生存冒险博得了广大玩家的青睐。然而,一些玩家在经历了一场惊心动魄的对局后,却面临了一个不大不…...
LAMP+phpMyAdmin部署)
24 Debian如何配置Apache2(4)LAMP+phpMyAdmin部署
作者:网络傅老师 特别提示:未经作者允许,不得转载任何内容。违者必究! Debian如何配置Apache2(4)LAMP+phpMyAdmin部署 《傅老师Debian小知识库系列之24》——原创 ==前言== 傅老师Debian小知识库特点: 1、最小化拆解Debian实用技能; 2、所有操作在VM虚拟机实测完成;…...

centos安装paddlespeech各种报错解决方案
背景 windows系统安装paddlespeech一路顺利 centos安装之前也是正常 今天centos再次安装各种报错,避免以后遇到浪费时间,记录下来,也给大家节约时间 报错 报错1 module numpy has no attribute complex. 解决方案 降低numpy # 1. 卸载当前numpy库 pip uninstall numpy…...

谈基于ATTCK框架的攻击链溯源
引言 网络安全在当今数字化时代变得尤为关键,而MITRE公司开发的ATT&CK框架则成为了安全专业人员的重要工具。ATT&CK是一种广泛使用的攻击行为分类和描述框架。其目的在于提供一个共同的语言,使安全专业人员能够更好地理解攻击者的行为和目标&…...

在Ubuntu下搭建自己的以太坊私有链
最近要对链及链上应用进行压测,为了方便操作及分析问题,就自己搭建了一个eth私链。当前版本安装官方指引发现有卡点,于是决定整理一个文档,为其他有需要的朋友提供便捷操作,节约时间。 一、环境配置 linux操作系统:Ubuntu 20.04.6 LTS (Focal Fossa) go version: go1…...

巩固学习4
python中函数逆置的几种方法 s input()for i in range(len(s)-1,-1,-1):#从最后一位开始,步长为-1print(s[i],end)用for语句循环逆置 s input() s list(s) n len(s) for i in range(n//2):s[i],s[n-1-i] s[n-1-i],s[i]#从中间反转字符串 res "".j…...

Conda安装rasterio报错
Conda安装rasterio报错 文章目录 Conda安装rasterio报错问题解决参考 问题 在conda环境中安装rasterio包之后,本来可以正常运行的,但是之后又重新安装了一个gdal,导致原来的引用rasterio的包的程序不可正常运行了 conda install rasterio c…...
linux安装 mysql
环境:centOS8 一、安装 1 安装wget库 sudo yum -y install wget 2. 安装 mysql 换yum源 亲测成功!!!!!! 换yum源 1.下载对应版本的repo文件 wget -O CentOS-Base.repo http://mirrors…...
暴力法解决最近对问题和凸包问题-实现可视化
目录 最近对问题 凸包问题 最近对问题 顾名思义就是采用蛮力法求出所有点之间的距离,然后进行比较找出第一个最近对,一个一个进行比较。 大概思路就是如图(每个圈代表一个数对) 第一个和其他四个比较 第二个和其他三个比较 …...
[Kubernetes] Rancher 2.7.5 部署 k8s
server: 192.168.66.100 master: 192.168.66.101 node1: 192.168.66.102 文章目录 1.rancher server 安装docker2.部署k8s3.kubeconfig4.测试集群 1.rancher server 安装docker 所有主机开通ipv4 vi /etc/sysctl.conf#加入 net.ipv4.ip_forward 1#配置生效 sysctl -prancher…...
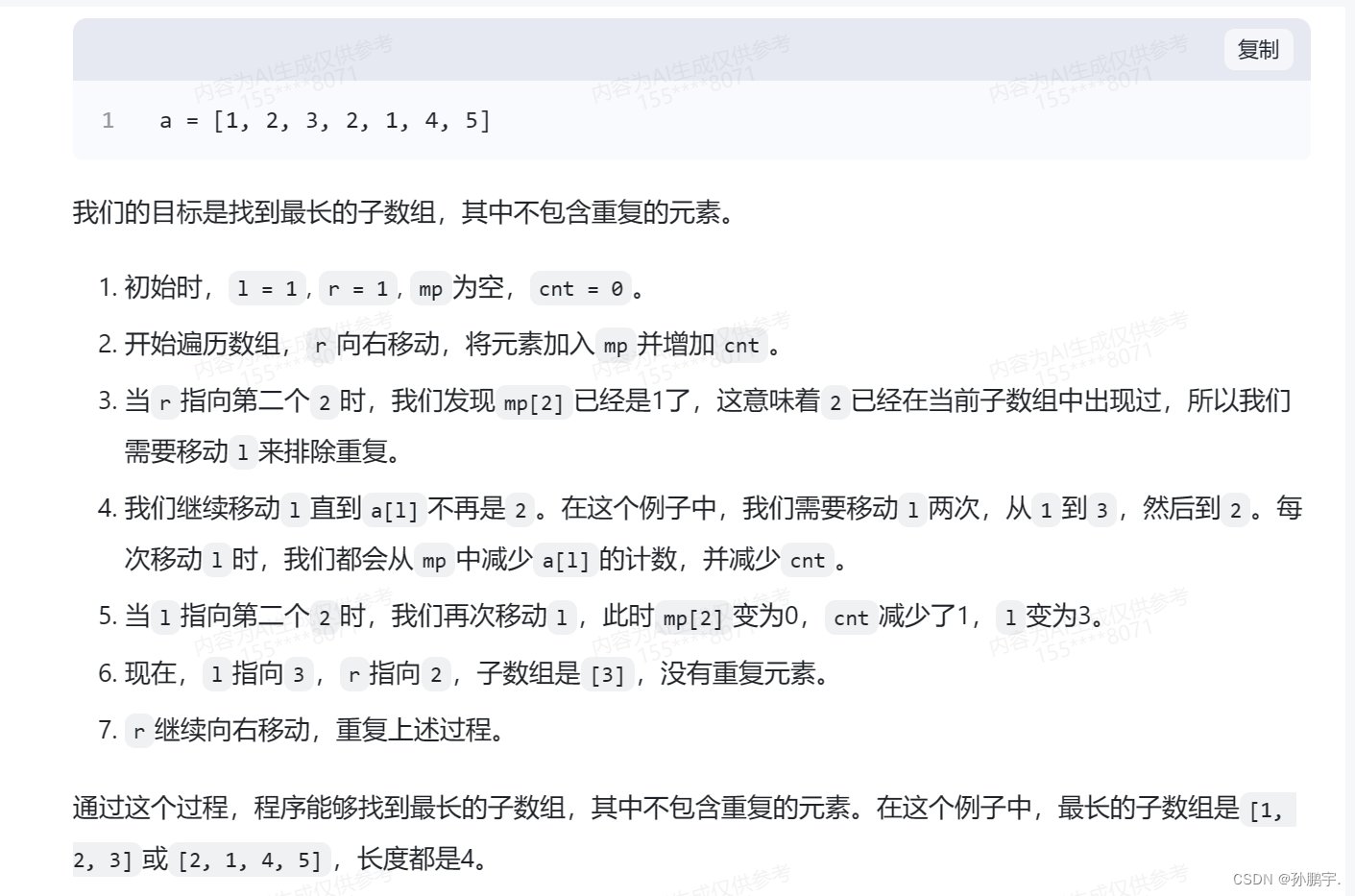
码题杯 世界警察 思想:双指针
https://www.matiji.net/exam/brushquestion/4/4446/16A92C42378232DEB56179D9C70DC45C 双指针 思路是这样的,首先r指针向右走,如果r指针遇到了和l指针一样的,那么l指针就,一直加到r指针的位置,此时a[l]a[r]࿰…...
drawio 网页版二次开发(1):源码下载和环境搭建
目录 一 说明 二 源码地址以及下载 三 开发环境搭建 1. 前端工程地址 2. 配置开发环境 (1)安装 node.js (2)安装 serve 服务器 3. 运行 四 最后 一 说明 应公司项目要求,需要对drawio进行二次开发&…...

算法训练Day33 |● 509. 斐波那契数 ● 70. 爬楼梯 ● 746. 使用最小花费爬楼梯
509. 斐波那契数 class Solution { public:int fib(int n) {if(n<1) return n;int pre2 0;int pre1 1;int result 0;for(int i2; i<n; i ){result pre1pre2;pre2 pre1;pre1 result;}return result;} };参考文章:代码随想录- 509. 斐波那契数 70. 爬楼梯…...
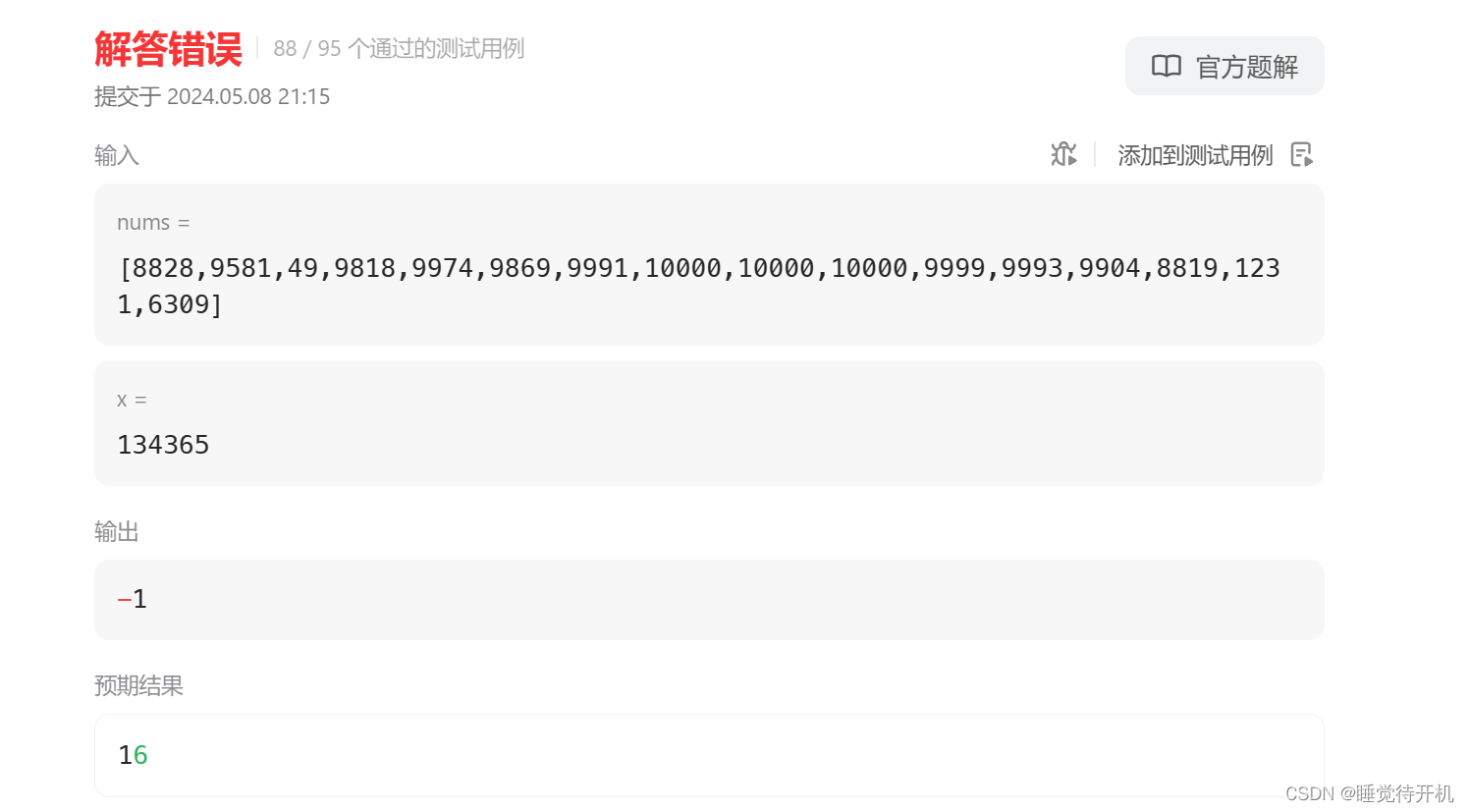
【算法】滑动窗口——将x减到0的最小操作数
本节博客主要是讲的我解“将x减到0的最小操作数”这道题的思路历程,从最开始的想法到代码提交的详细记录,有需要借鉴即可。 目录 1.题目2.代码示例3.细节3.1left越界3.2特殊情况 4.总结 1.题目 题目链接:LINK 看题目意思是就是给你一个数X&…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...
 + 力扣解决)
LRU 缓存机制详解与实现(Java版) + 力扣解决
📌 LRU 缓存机制详解与实现(Java版) 一、📖 问题背景 在日常开发中,我们经常会使用 缓存(Cache) 来提升性能。但由于内存有限,缓存不可能无限增长,于是需要策略决定&am…...

【学习笔记】erase 删除顺序迭代器后迭代器失效的解决方案
目录 使用 erase 返回值继续迭代使用索引进行遍历 我们知道类似 vector 的顺序迭代器被删除后,迭代器会失效,因为顺序迭代器在内存中是连续存储的,元素删除后,后续元素会前移。 但一些场景中,我们又需要在执行删除操作…...

Golang——7、包与接口详解
包与接口详解 1、Golang包详解1.1、Golang中包的定义和介绍1.2、Golang包管理工具go mod1.3、Golang中自定义包1.4、Golang中使用第三包1.5、init函数 2、接口详解2.1、接口的定义2.2、空接口2.3、类型断言2.4、结构体值接收者和指针接收者实现接口的区别2.5、一个结构体实现多…...
