数论:不定方程的引入
研究的对象:不定方程
文章目录
- 研究的对象:不定方程
- 不定方程引入:
- 裴蜀定理证明:
- 欧几里得算法证明:
- 充分性证明:
- 必要性证明:
- 战术总结:
不定方程引入:
不定方程,又称丢番图方程,定义为:未知数为整数,系数也为整数的多项式等式。
形如 a 1 x 1 b 1 + a 2 x 2 b 2 + . . . + a n x n b n = c a_1x_1^{b_1} + a_2x_2^{b_2}+...+a_nx_n^{b_n} =c a1x1b1+a2x2b2+...+anxnbn=c
如果我们能找到一组整数解: x 1 , x 2 , . . . , x n x_1,x_2,...,x_n x1,x2,...,xn,我们就说这个方程有解。
但是我们并不研究不定方程的一般式,而是研究其特殊的形式,即一次不定方程:
a 1 x 1 + a 2 x 2 + . . . + a n x n = c a_1x_1 + a_2x_2+...+a_nx_n =c a1x1+a2x2+...+anxn=c
这个一次不定方程有解的充要条件是:
g c d ( a 1 , a 2 , . . , a m ) ∣ c gcd(a_1,a_2,..,a_m)|c gcd(a1,a2,..,am)∣c (即c为这n个数的倍数的时候,该一次不定方程有解)
这个推论是由二元一次不定方程有解的情况归纳而来:
即:
对于二元一次不定方程: a x + b y = c ax+by=c ax+by=c
此方程有解的充要条件是 : g c d ( a , b ) ∣ c gcd(a,b)|c gcd(a,b)∣c
这个结论是裴蜀定理的证明:下面将引出裴蜀定理。
裴蜀定理与不定方程的解有什么关系??
裴蜀定理给出:
对于任何整数 a , b , m a,b,m a,b,m,关于未知数 x , y x,y x,y 的一元二次不定方程 a x + b y = m ax+by = m ax+by=m
此方程有解的充要条件是 g c d ( a , b ) ∣ m gcd(a,b)|m gcd(a,b)∣m,由于只给了一个不定方程,所以整数解有无穷多个,每一组(x,y)都被称为裴蜀数。
裴蜀定理证明:
由于是任意整数 a , b a,b a,b
所以我们先考虑0的情况:
1、当 a = 0 a = 0 a=0
该不定方程为: b y = m by = m by=m , 此方程有整数解,当且仅当 b ∣ m b\:|\:m b∣m 。
可以写成 g c d ( 0 , b ) ∣ m gcd(0,b)|m gcd(0,b)∣m
写到这里突然有个想法, g c d ( 0 , b ) gcd(0,b) gcd(0,b) 这样的写法是合法的吗?
公约数的定义:如果有一个数 d d d, 对于 a 1 , a 2 , a 3 , . . . , a n a_1,a_2,a_3,...,a_n a1,a2,a3,...,an,都有 d ∣ a i , i ∈ [ 1 , n ] d|a_i,i\in[1,n] d∣ai,i∈[1,n]
这样的数就被称为这些数的公约数。
将 a 1 , a 2 , a 3 , . . . , a n a_1,a_2,a_3,...,a_n a1,a2,a3,...,an的所有公约数放入集合 D D D中, D = { d ; d ∣ ( a 1 , a 2 , a 3 , . . . a n ) } D=\lbrace d;d|(a_1,a_2,a_3,...a_n)\rbrace D={d;d∣(a1,a2,a3,...an)}
最大公约数gcd的定义是: d m a x ∈ D d_{max}\in D dmax∈D,使得 ∀ d ∣ d m a x \forall d|d_{max} ∀d∣dmax,其中 d m a x d_{max} dmax被称为 g c d gcd gcd。
0 0 0能被任意非 0 0 0数整除, b b b最大只能被 b b b整除。
当只要求 2 2 2个整数的最大公约数的时候,有一方为 0 0 0,那么它们的最大公因数就是另一个非零数本身。
都讲到这里了,顺便在写一下欧几里得算法的证明:
欧几里得算法证明:
考虑 g c d ( a , b ) = g c d ( b , a m o d b ) gcd(a,b) = gcd(b,a\:mod\:b) gcd(a,b)=gcd(b,amodb) 的证明:(面向结果证明)
任意一个整数可以写成带余除法(因为要用到 a m o d b a\:mod\:b amodb 的形式,所以将 a a a写成关于 b b b的带余除法: a = k b + c a = kb+c a=kb+c , c = a m o d b c = a \:mod \:b c=amodb 并约定 ( b ≠ 0 ) (b\neq0) (b=0)。
设 d d d 是 a , b a,b a,b的最大公约数。
有: d ∣ a , d ∣ b d|a ,\: d|b d∣a,d∣b。
两边同时除以d: a d = k b d + c d \frac{a}{d} = k\frac{b}{d}+\frac{c}{d} da=kdb+dc。
由于 a d , b d \frac{a}{d},\frac{b}{d} da,db都是整数,所以 c d \frac{c}{d} dc也是一个整数。
这说明 d ∣ c d|c d∣c , 这说明 d d d 是 ( a , b , c ) (a,b,c) (a,b,c)的最大公约数。
所以得到了最终的转移式子: g c d ( a , b ) = g c d ( b , c ) gcd(a,b) = gcd(b,c) gcd(a,b)=gcd(b,c)
这个证明过程告诉我们,不要忽视整数这个性质
2、当 b = 0 b = 0 b=0 的时候,这与 a = 0 a = 0 a=0 的计算过程等价,结论也等价,所以不过多赘述。
3、下面讨论 a ≠ 0 , b ≠ 0 a\neq0,b\neq0 a=0,b=0 的情况:
再次重申我们要证明的是什么?(有时候写着写着忘记要干嘛了)
证明: a x + b y = c ax + by = c ax+by=c 有整数解 ( x , y ) ⇔ g c d ( a , b ) ∣ c (x,y)\Leftrightarrow gcd(a,b)|c (x,y)⇔gcd(a,b)∣c
充分性证明:
证明充分性,即证明: a x + b y = c ⇒ g c d ( a , b ) ∣ c ax+by=c \Rightarrow gcd(a,b)|c ax+by=c⇒gcd(a,b)∣c
假设 a x + b y = c ax+by=c ax+by=c有解。
设 A = { a x + b y ; ( x , y ) ∈ Z 2 } A = \lbrace ax+by ; (x,y)\in \Z^2 \rbrace A={ax+by;(x,y)∈Z2}
不妨设 c 0 c_0 c0为 A A A的最小正整数元素: a x 0 + b y 0 = c ax_0+by_0=c ax0+by0=c,其中 c c c表示A的任意一个正整数元素: a x + b y = c ax+by=c ax+by=c。
作 c c c对 c 0 c_0 c0的带余除法: c = q c 0 + r c = qc_0 + r c=qc0+r , 0 ≤ r < c 0 0 \leq r< c_0 0≤r<c0
代入原式: a x + b y = q ( a x 0 + b y 0 ) + r ax+by = q(ax_0+by_0) + r ax+by=q(ax0+by0)+r
r = a ( x − q x 0 ) + b ( y − q y 0 ) r = a(x-qx_0) + b(y - qy_0) r=a(x−qx0)+b(y−qy0) ,显然满足 r ∈ A r\in A r∈A
∵ \because ∵ 0 ≤ r < c 0 0\leq r< c_0 0≤r<c0 ,而 c 0 c_0 c0是 A A A中的最小正元素。
∴ \therefore ∴ r r r 不是正元素, 即 r = 0 r=0 r=0,所以 c c c对 c 0 c_0 c0的带余除法为: c = q c 0 c=qc_0 c=qc0
也就是说 A A A中任意一个正元素 c c c,都存在 c 0 ∣ c c_0|c c0∣c。
∵ a x + b y = c , ∀ c ∈ A , c 0 ∣ c \because ax+by=c , \forall c\in A ,c_0|c ∵ax+by=c,∀c∈A,c0∣c
∴ \therefore ∴ , c 0 ∣ a x c_0 |ax c0∣ax , c 0 ∣ b y c_0|by c0∣by
∵ x , y ∈ Z \because x,y\in\Z ∵x,y∈Z
∴ c 0 ∣ a , c 0 ∣ b \therefore c_0|a,c_0|b ∴c0∣a,c0∣b 即 c c c 是 a , b a,b a,b的公约数。
这是一个关键的进展!
接下来,我们只要证明 g c d ( a , b ) = c 0 gcd(a,b)=c_0 gcd(a,b)=c0
就能得到: g c d ( a , b ) ∣ c gcd(a,b)|c gcd(a,b)∣c
设 d d d为 a , b a,b a,b的任意正公约数, a = k d , b = l d a=kd,b=ld a=kd,b=ld。
a x + b y = k d x + l d y = ( k x + l y ) d = c 0 ax + by = kdx+ldy=(kx+ly)d=c_0 ax+by=kdx+ldy=(kx+ly)d=c0
∴ d ∣ c 0 \therefore d|c_0 ∴d∣c0
∴ g c d ( a , b ) = c 0 \therefore gcd(a,b)=c_0 ∴gcd(a,b)=c0
∴ ∀ a , b , c ∈ Z , a x + b y = c \therefore \forall a,b,c\in \Z , \:ax+by=c ∴∀a,b,c∈Z,ax+by=c 有解 ⇒ g c d ( a , b ) ∣ c \Rightarrow gcd(a,b)|c ⇒gcd(a,b)∣c
充分性证毕
必要性证明:
证明当 g c d ( a , b ) ∣ c gcd(a,b)|c gcd(a,b)∣c的时候, a x + b y = c ax+by=c ax+by=c 有解:
这个问题等价于证明:当 g c d ( a , b ) = c 0 gcd(a,b)=c_0 gcd(a,b)=c0时, a x + b y = c 0 ax+by=c_0 ax+by=c0有解:
设 d = g c d ( a , b ) d = gcd(a,b) d=gcd(a,b)
等式两边同时除以 d d d,等式就被转换为: a ′ x + b ′ y = 1 a'x+b'y=1 a′x+b′y=1 其中 g c d ( a ′ , b ′ ) = 1 gcd(a',b')=1 gcd(a′,b′)=1
问题就转化为证明这个等式成立: a ′ x + b ′ y = 1 a'x+b'y=1 a′x+b′y=1。
这个求解的过程可以由欧几里得算法顺带求出。
令 a ′ = a , b ′ = b a'=a,b'=b a′=a,b′=b
模拟求 g c d ( a , b ) gcd(a,b) gcd(a,b)的过程:
a = k 1 b + r 1 a = k_1b+r_1 a=k1b+r1
⇒ a = b , b = r 1 \Rightarrow a=b,b=r_1 ⇒a=b,b=r1
b = k 2 r 1 + r 2 b=k_2r_1+r_2 b=k2r1+r2
r 1 = k 3 r 2 + r 3 r_1=k_3r_2+r_3 r1=k3r2+r3
. . . ... ...
r n − 1 = k n + 1 r n + r n + 1 . . . ( 3 ) r_{n-1}=k_{n+1}r_{n}+r_{n+1}...(3) rn−1=kn+1rn+rn+1...(3)
r n = k n + 2 r n + 1 + r n + 2 . . . . ( 2 ) r_n=k_{n+2}r_{n+1}+r_{n+2}....(2) rn=kn+2rn+1+rn+2....(2)
r n + 1 = k n + 3 r n + 2 . . . ( 1 ) r_{n+1}=k_{n+3}r_{n+2}...(1) rn+1=kn+3rn+2...(1)
g c d = r n + 2 gcd = r_{n+2} gcd=rn+2
欧几里得算法在 r = 0 r=0 r=0的时候停止,并返回 b b b,也就是 ( 1 ) (1) (1)式子
所以,可以得到 r n + 2 = 1 r_{n+2}=1 rn+2=1
r n = k n + 2 r n + 1 + 1... ( 2 ) r_{n}=k_{n+2}r_{n+1}+1...(2) rn=kn+2rn+1+1...(2)
联立 ( 2 ) , ( 3 ) (2),(3) (2),(3)消去 r n + 1 r_{n+1} rn+1:
{ k n + 2 r n + 1 = 1 − r n k n + 2 r n + 1 = k n + 2 r n − 1 − k n + 1 k n + 2 r n \begin{cases} k_{n+2}r_{n+1}=1-r_n\\ k_{n+2}r_{n+1}=k_{n+2}r_{n-1}-k_{n+1}k_{n+2}r_n \end{cases} {kn+2rn+1=1−rnkn+2rn+1=kn+2rn−1−kn+1kn+2rn
得:
( k n + 2 k n + 1 − 1 ) r n + 1 = k n + 2 r n − 1 . . . ( 1 ′ ) (k_{n+2}k_{n+1}-1)r_n+1=k_{n+2}r_{n-1}...(1') (kn+2kn+1−1)rn+1=kn+2rn−1...(1′)
联立 ( 1 ′ ) , ( 3 ) (1'),(3) (1′),(3)消去 r n r_n rn:
{ r n − 2 = k n r n − 1 + r n ( k n + 2 k n + 1 − 1 ) r n + 1 = k n + 2 r n − 1 \begin{cases} r_{n-2} = k_{n}r_{n-1}+r_n\\ (k_{n+2}k_{n+1}-1)r_n+1=k_{n+2}r_{n-1} \end{cases} {rn−2=knrn−1+rn(kn+2kn+1−1)rn+1=kn+2rn−1
得:
( k n + 2 k n + 1 − 1 ) r n − 2 + 1 = ( k n + 2 k n + 1 k n − k n + k n + 2 ) r n − 1 . . . ( 2 ′ ) (k_{n+2}k_{n+1}-1)r_{n-2}+1=(k_{n+2}k_{n+1}k_{n}-k_n+k_{n+2})r_{n-1}...(2')\\ (kn+2kn+1−1)rn−2+1=(kn+2kn+1kn−kn+kn+2)rn−1...(2′)
我们观察式子的结构不难发现:这个式子只包含 r i , r i − 1 r_i,r_{i-1} ri,ri−1这两个已知量,以及常数1,以及 r i , r i − 1 r_i,r_{i-1} ri,ri−1前面的系数。
所以,我们可以通过不断的消去 r i r_i ri,使得最终的式子只包含 ( a , b , k ) (a,b,k) (a,b,k)。
最终的形式一定可以化简: a x + b y = 1 ax+by=1 ax+by=1。
必要性证毕。
战术总结:
本节内容的主要内容如下:
1、不定方程的简单介绍。
2、裴蜀定理介绍。
3、裴蜀定理的证明:
先证明充分性:
- 假定 a x + b y = c ax+by=c ax+by=c有解,证出 ∀ c ∈ A , c 0 ∣ c \forall c\in A,c_0|c ∀c∈A,c0∣c,进而得出 c 0 ∣ a , c 0 ∣ b c_0|a,c_0|b c0∣a,c0∣b,即 c 0 c_0 c0是 a , b a,b a,b的公约数
- 接着证明 a , b a,b a,b的任意约数 d d d,都有 d ∣ c 0 d|c_0 d∣c0,得出 c 0 c_0 c0是 a , b a,b a,b的最大公约数。
- 此时证出:若 a x + b y = c 0 ax+by=c_0 ax+by=c0有解,则 c 0 = g c d ( a , b ) c_0=gcd(a,b) c0=gcd(a,b)
- 在等式两边乘以任意整数可得:若 a x + b y = c ax+by=c ax+by=c有解,则 g c d ( a , b ) ∣ c gcd(a,b)|c gcd(a,b)∣c
再证明必要性:
- 即证明当 c 0 = g c d ( a , b ) c_0=gcd(a,b) c0=gcd(a,b)的时候,是否 a x + b y = c 0 ax+by=c_0 ax+by=c0成立
- 两边除以 c 0 c_0 c0,问题便转为证明:当 g c d ( a , b ) = 1 gcd(a,b)=1 gcd(a,b)=1 时, a ′ x + b ′ y = 1 a'x+b'y=1 a′x+b′y=1成立。
- 这个等式由欧几里得算法可以得出是有解的。
相关文章:

数论:不定方程的引入
研究的对象:不定方程 文章目录 研究的对象:不定方程不定方程引入:裴蜀定理证明:欧几里得算法证明:充分性证明:必要性证明: 战术总结: 不定方程引入: 不定方程࿰…...
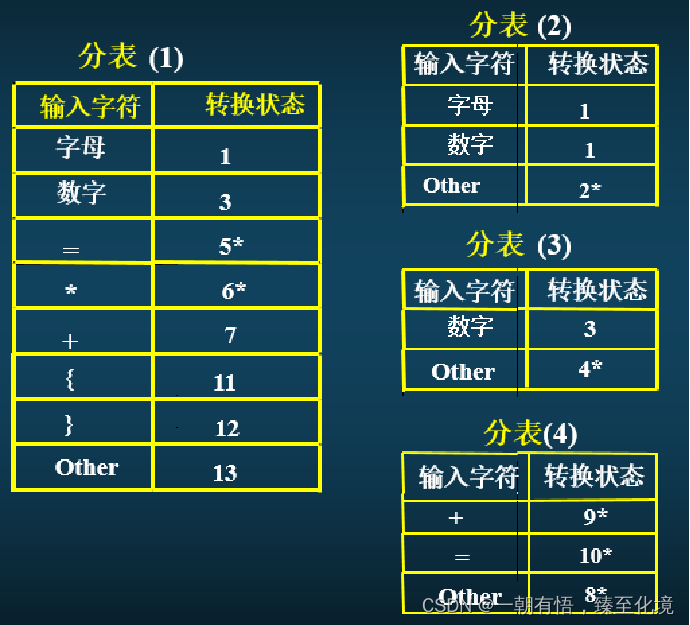
数据中心法
数据中心法是实现词法分析器的结构化方法。通过设计主表和子表分开存储状态转移信息,实现词法分析器的控制逻辑和数据结构分离。 主要解决了状态爆炸、难以维护和复杂性的问题。 状态爆炸是指当状态和转移较多时,单一使用一个表来存储所有的信息的话会导…...
pdffactory pro8.0虚拟打印机(附注册码)
PdfFactory pro是一款非常受欢迎的PDF虚拟打印机,可以帮助用户将你的其他文档保存为PDF格式。请为用户提供打印/发送/加密等多种实用功能,以及一套完善的PDF打印方案。 使用说明 下载pdfFactory Pro压缩包,解压后,双击exe文件&am…...

处理用户输入
目录 一、传递参数 1.1 读取参数 1.2 读取脚本名 二、跟踪参数 三、移动参数 四、处理选项 4.1 查找选项 4.1.1 处理简单选项 4.1.2 分离参数和选项 4.1.3 处理含值的选项 五、选项标准化 5.1 使用 getopt 命令 5.1.1 命令格式 5.1.2 在脚本中使用getopt 5.2 使用…...
在装有centOS7的虚拟机上进行MySQL的安装部署
1.MySQL数据库介绍 1.开源的,跨平台的,社区版免费 2.支持多种存储引擎 3.支持多种主从复制 MySQL版本:5.6 5.7 8.0 https://www.mysql.com MySQL官网 2.安装MySQL5.7 1.配置MySQL仓库 2.安装MySQL服务端软件 3.启动MySQL服务 s…...

【vivado】debug相关时钟及其约束关系
一、前言 在xilinx fpga的degug过程中,经常出现由于时钟不对而导致的观测波形失败,要想能够解决这些问题需要了解其debug的组成环境以及之间的数据流。本文主要介绍debug过程中需要的时钟及各时钟之间的关系。 二、debug相关时钟 Vivado 硬件管理器使…...
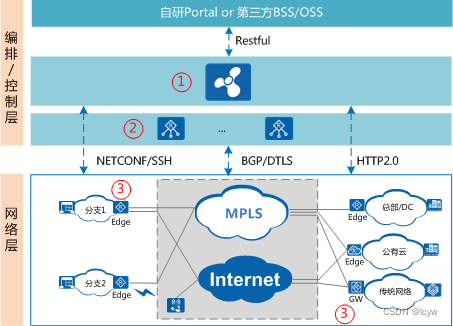
什么是HTTP/2?
HTTP/2(原名HTTP 2.0)即超文本传输协议第二版,使用于万维网。HTTP/2主要基于SPDY协议,通过对HTTP头字段进行数据压缩、对数据传输采用多路复用和增加服务端推送等举措,来减少网络延迟,提高客户端的页面加载…...
【ChatGPT with Date】使用 ChatGPT 时显示消息时间的插件
文章目录 1. 介绍2. 使用方法2.1 安装 Tampermonkey2.2 安装脚本2.3 使用 3. 详细文档指引4. 反馈5. 未来计划6. 开源协议X. Changelog 1. 介绍 有时我们希望看到 ChatGPT 的消息时间,但 ChatGPT 并没有显示消息时间的功能。 本项目通过 Tampermonkey 开发…...

STM:TIM定时器——定时中断
文章目录 1、TIM定时器1.1定时器类型1.2定时中断的基本结构 2 定时器初始化2.2 初始化定时器的步骤2.3 TIM库函数2.4 配置TIM2.4.1 Timer.c2.4.2 Timer.c2.4.3 main.c 1、TIM定时器 定时器的功能可以对输入的时钟进行计数,并在计数值达到设定值时触发中断。 他包含…...
jetson tx2 nx实现在ros1中yolov5实现
亲测用以下链接实现功能。 安装ros。Ubuntu18.04安装ROS Melodic(详细,亲测安装完成,有清晰的截图步骤)_ubuntu 18 ros melodic-CSDN博客文章浏览阅读10w次,点赞835次,收藏3.8k次。这也是我在ubuntu里面安…...

【SpringBoot笔记43】SpringBoot应用程序集成spring-boot-admin监控工具
这篇文章,主要介绍SpringBoot应用程序如何集成spring-boot-admin监控工具。 目录 一、spring-boot-admin监控工具 1.1、创建admin-client客户端 (1)引入依赖...
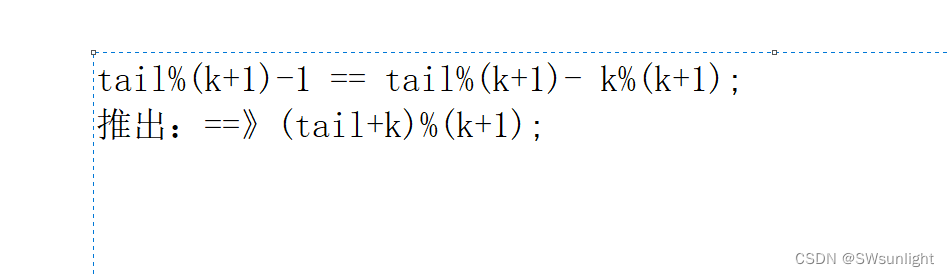
与队列和栈相关的【OJ题】
✨✨✨专栏:数据结构 🧑🎓个人主页:SWsunlight 目录 一、用队列实现栈: 1、2个队列的关联起来怎么由先进先出转变为先进后出:(核心) 2、认识各个函数干嘛用的: …...

Unity编辑器扩展
Unity编辑器扩展是指为Unity引擎开发者提供的一种扩展功能,可以增强Unity编辑器的功能和效能。这些扩展可以帮助开发者提高工作效率,简化工作流程,并提供更好的用户体验。本文将介绍Unity编辑器扩展的基本概念、开发流程以及一些常见的应用示…...
)
【kettle】kettle访问数据库系列文章及视频地址(更新中)
1.一直以来想写下基于kettle的系列文章,作为较火的数据ETL工具,也是日常项目开发中常用的一款工具,最近刚好挤时间梳理、总结下这块儿的知识体系。 2.这里整理了kettle访问数据库系列文章及视频地址整体链接,并及时补充、更新相关…...

共赴科技盛会“2024南京智博会”11月在南京国际博览中心召开
2024年,南京这座历史悠久的文化名城迎来了一场科技与智慧交织的盛会——南京智博会|南京国际智慧城市、物联网、大数据。本次博览会以智慧城市、人工智能、消费电子、物联网、大数据为主题,汇聚了全球各地的智能科技精英,共同探讨智慧城市建设…...
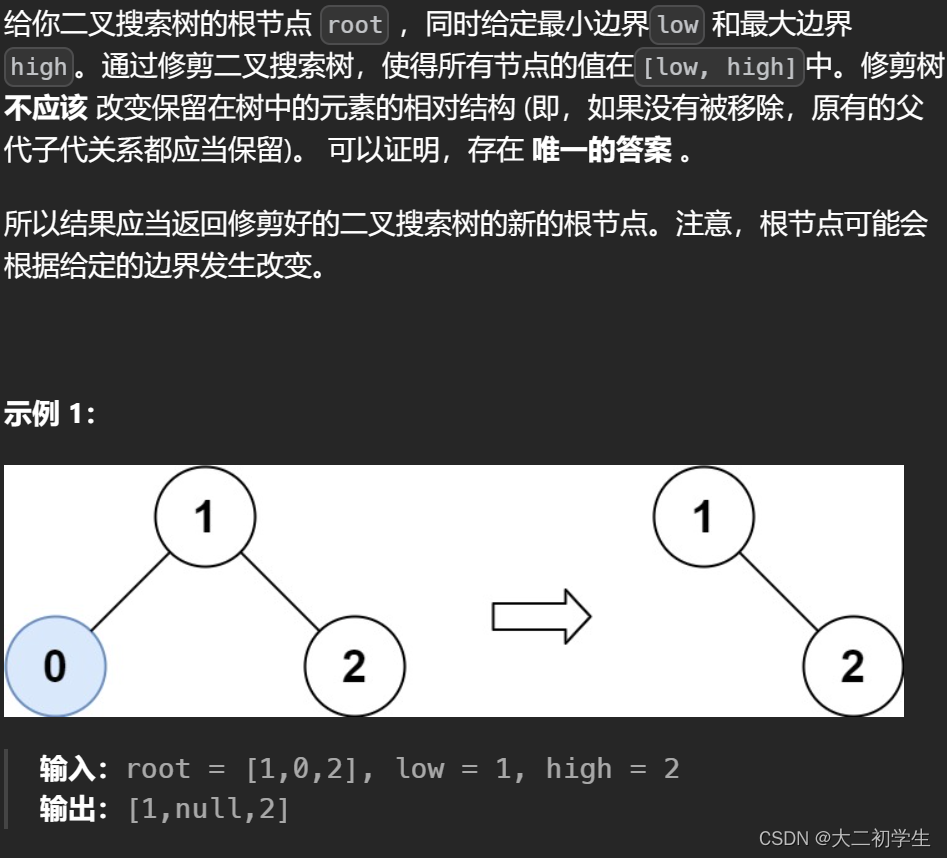
刷代码随想录有感(62):修建二叉搜索树
题干: 代码: class Solution { public:TreeNode* traversal(TreeNode* root, int low, int high){if(root NULL)return NULL;if(root->val < low)return traversal(root->right, low, high);if(root->val > high)return traversal(ro…...
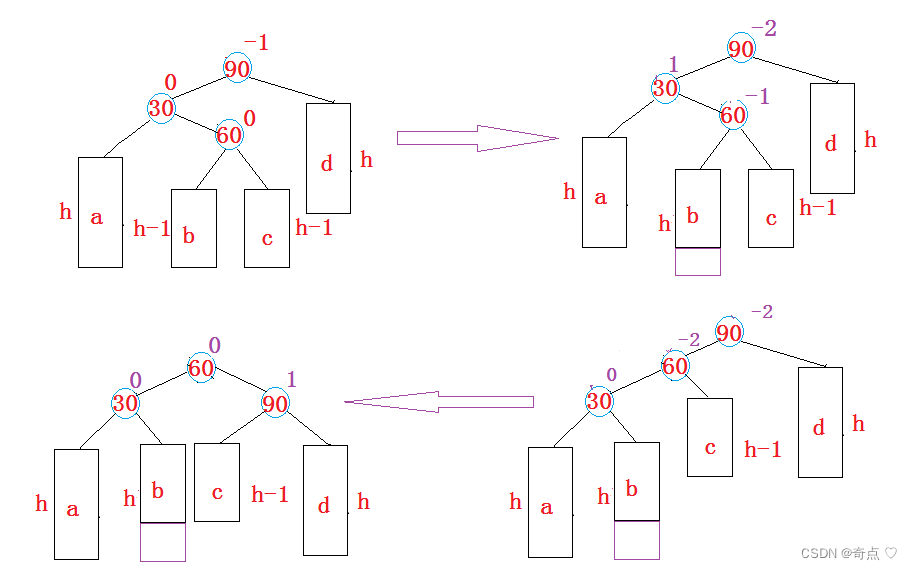
AVL树的旋转
目录 1.平衡因子 2.旋转 a.节点定义 b.插入 插入 平衡因子更新 旋转 左单旋 右单旋 右左双旋 左右双旋 3.AVL树的验证 1.平衡因子 我们知道搜索二叉树有缺陷,就是不平衡,比如下面的树 什么是搜索树的平衡?就是每个节点的左右子树的…...
)
C++(动态规划之拆分整数)
其实我交上去都有点似懂非懂 题目:(343. 整数拆分 - 力扣(LeetCode)) 给定一个正整数 n ,将其拆分为 k 个 正整数 的和( k > 2 ),并使这些整数的乘积最大化。 返回 …...

unix C之环境变量
什么是环境变量 每个进程都有自己的一张环境变量表,表中的每个条目都是形如 keyvalue 的键值对形式的环境变量。 进程可以通过环境变量访问计算机资源。 在终端下输入env命令,可以查看环境变量列表。 通过echo $name 可以查看某个环境变量的值。 环…...

Flutter实战记录-协作开发遇到的问题
一.前言 Android项目使用了混合架构,部分模块使用Flutter进行开发。在电脑A上开发的项目提交到git仓库,电脑B拉取后进行操作,遇到两个问题,特此做一下记录; 二.问题A Settings file ‘D:\xxx\settings.gradle’ line…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...
