STM:TIM定时器——定时中断
文章目录
- 1、TIM定时器
- 1.1定时器类型
- 1.2定时中断的基本结构
- 2 定时器初始化
- 2.2 初始化定时器的步骤
- 2.3 TIM库函数
- 2.4 配置TIM
- 2.4.1 Timer.c
- 2.4.2 Timer.c
- 2.4.3 main.c
1、TIM定时器
定时器的功能可以对输入的时钟进行计数,并在计数值达到设定值时触发中断。
- 他包含16位计数器(CNT)、预分频器(PSC)、自动重装寄存器(ARR)的时基单元,在72MHz计数时钟下可以实现最大59.65s的定时。
- 不仅具备基本的定时中断功能,而且还包含内外时钟源选择、输入捕获、输出比较、编码器接口、主从触发模式等多种功能。
- 根据复杂度和应用场景分为了高级定时器、通用定时器、基本定时器三种类型。
计数器(CNT):用来执行计数定时的一个寄存器,每来一个时钟,计数器加1;
预分频器(PSC):对计数器的时钟进行分频,使奇数更加灵活;
自动重装寄存器(RCC):使计数值的目标值,也就是想要多少个时钟申请中断。
1.1定时器类型

- STM32F103C8T6定时器资源有:TIM1、TIM2、TIM3、TIM4
基本定时器从基准时钟,到预分频器,再到计数器,计数器计数自增,同时不断地与自动重装寄存器进行比较;他们相等时,即计时时间到,这时会产生一个更新中断和中断事件,CPU响应更新中断,最后完成定时中断的任务。基本定时器仅支持向上计数这一模式。
通用定时器和高级定时器不仅支持向上计数模式,还支持向下计数模式和中央对齐模式。
STM32定时器的一大特色,就是主从触发模式DAC的功能,他能让硬件在不受程序的控制下实现自动运行。如果运用得当,在某些情景下可以极大的减轻CPU的负担。
1.2定时中断的基本结构
定时中断和内外时钟源选择所涉及的结构如下图所示:
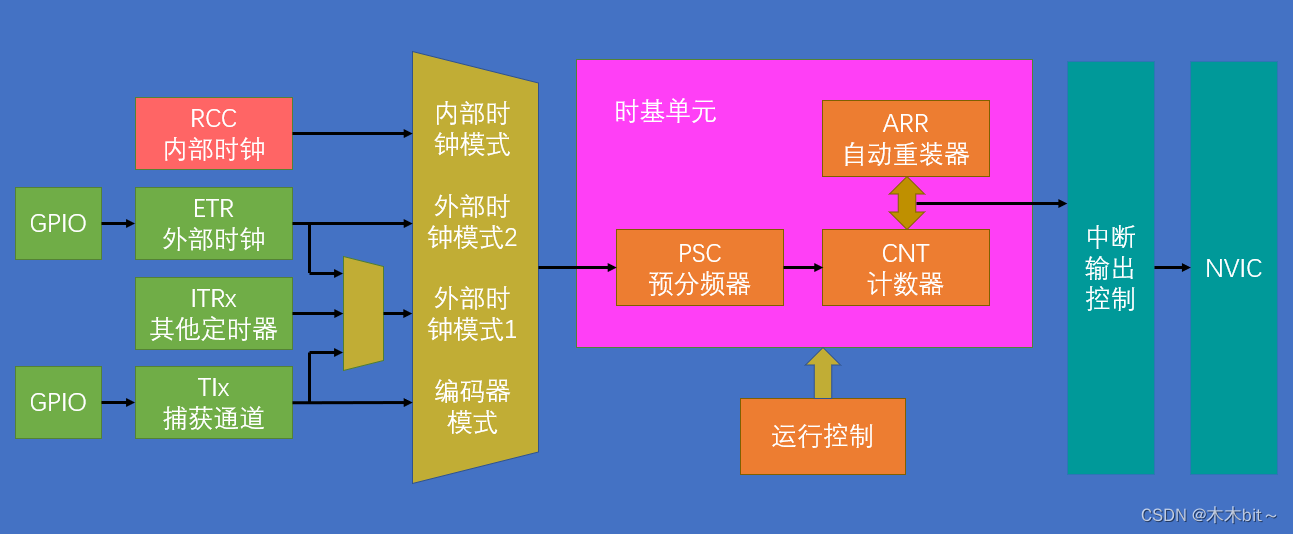
PSC、CNT和ARR三个部分构成了时基单元;下面是运行控制,控制寄存器的一些位,比如启动停止、向上或向下计数等等,操作这些寄存器就能控制时基单元的运行了。
左边是为时基单元提供时钟的部分;右边是计时时间到,产生新更新中断后的信号去向。如果是高级定时器,在右边部分还会多一个重复计数器。
2 定时器初始化
我们通过定时中断的整个框架结构图,将图中的每个模块都打通,就能让定时器工作了。
2.2 初始化定时器的步骤
这里以初始化TIM2定时器为例:
1.RCC开启时钟,TM2是APB1总线的外设,所以要使用APB1的开启时钟函数;
2.选择时基单元的时钟源,对于定时中断,我们就选择内部时钟源;
3.配置时基单元,包括其中的PSC、ARR、CNT等等;
4.配置输出中断控制,允许更新中断输出到NVIC;
5.配置NVIC,在NVIC中打开定时器中断的通道,并分配一个优先级;
6.运行控制,整个模块配置完成后,需要使能一下计数器;当定时器使能后,计数器就会开始计数,当计数器更新时,触发中断;最后写一个定时器的中断函数,这样这个中断函数每隔一段时间就能自动执行一次了。
2.3 TIM库函数
下面我们来介绍一部分与TIM有关的库函数:
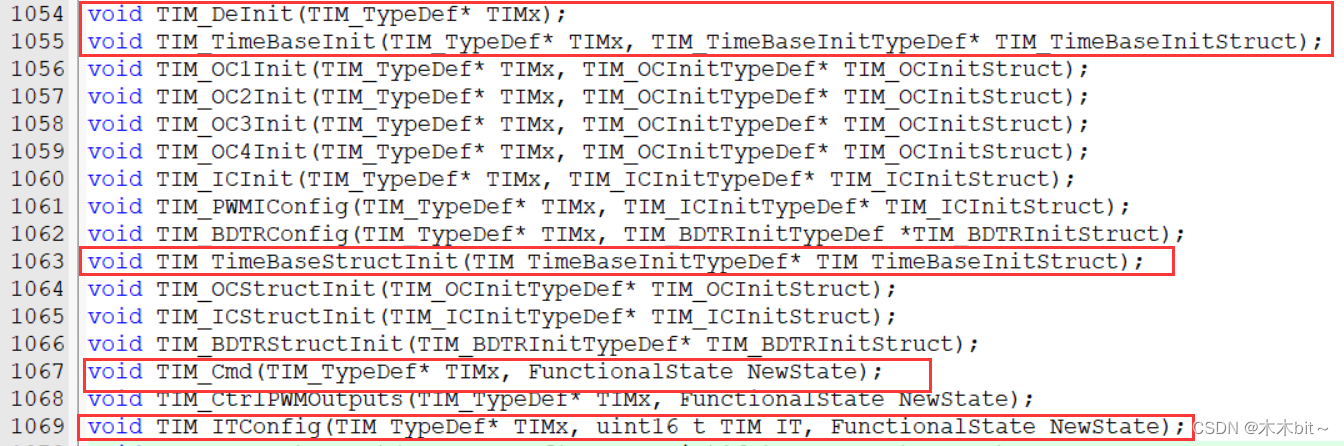
1.TIM_DeInit,恢复缺省配置。
2.TIM_TimeBaseInit,时基单元初始化,有两个参数,第一个TIMx选择某个定时器,第二个是结构体,包含了配置时基单元的一些参数。
3.TIM_TimeBaseStructInit,可以把结构体赋一个默认值。
4.TIM_Cmd,使能计数器,2个参数,第一个TIMx选择定时器;第二个NewState新的状态,也就是选择使能或者失能。
5.TIM_ITConfig,用来使能输出信号,3个参数,第一个TIMx,选择定时器;第二个TIM_IT,选择配置哪个中断输出;第三个NewState,新的状态选择使能还是失能。

6.TIM_InternalClockConfig,选择内部时钟。
7.TIM_ITRxExternalClockConfig,选择TIMx其他定时器的时钟,第一个参数选择要配置的定时器;第二个参数选择要接入哪个其他的定时器。
8.TIM_TIxExternalClockConfig,选择TIx捕获通道的时钟,4个参数,第一个参数TIMx;第二个参数选择TIx的某个引脚;第三个参数,选择输入的极性;第四个参数,选择滤波器。
9.TIM_ETRClockMode1Config,选择ETR通过外部时钟模式1输入的时钟,4个参数,第一个参数TIMx;第二个参数外部触发预分频器,这里可以对ETR的外部时钟再提前做一个分频;第三、四个参数分别是选择极性和滤波器。
10.TIM_ETRClockMode2Config,选择ETR通过外部时钟模式2输入的时钟,参数与上面一样。
11.TIM_ETRConfig,单独用来配置ETR引脚的预分频器、极性、滤波器等参数。
总结:
1、第6-11个函数,总共6个函数,对应的是时基单元的时钟选择部分,可选择RCC内部时钟、ETR外部时钟、ITRx其他定时器、ITx捕获通道等。
2、第9-10个函数,总共2个函数,对于ETR外部时钟而言,这两个函数是等效的,参数也是一样的;若不需要触发输入的功能,那么这两个函数原则上是可以互换的。
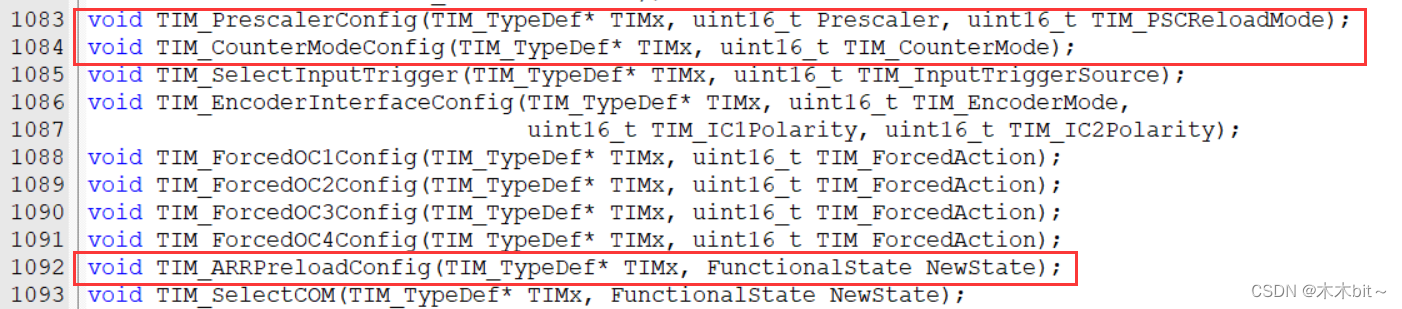
12.TIM_PrescalerConfig,单独写预分频的值,第二个参数就是要写入预分频的值;第三个参数是选择写入的模式。预分频器有一个缓冲器,写入的值是在更新事件发生后才有效的,所以这里有个写入模式,可以选择听从安排在更新事件生效;或是在写入后,手动产生一个更新事件,让这个值立刻生效。
13.TIM_CounterModeConfig,用来改变计数器的计数模式,第二个参数用来选择新的计数器模式。
14.TIM_ARRPreloadConfig,自动重装器预装功能配置。

15.TIM_SetCounter,给计数器写入一个值。
16.TIM_SetAutoreload,给自动重装器写入一个值。

17.uint16_t TIM_GetCounter,获取当前计数器的值,他的返回值就是当前计数器的值。
18.uint16_t TIM_GetPrescaler,获取当前预分频器的值。

19.FlagStatus TIM_GetFlagStatus
20.TIM_ClearFlag,主要用于清除定时器的中断标志位。
21.ITStatus TIM_GetITStatus
22.TIM_ClearITPendingBit,主要用于清除中断线路的中断挂起位。
这4个函数是用来获取标志位和清除标志位。
2.4 配置TIM
我们定一个时间,让定时器每隔一个时间产生中断,来实现每隔一个固定时间执行一段程序,如下:
2.4.1 Timer.c
#include "stm32f10x.h" void Timer_Init(void)
{
//1.开启时钟RCC_APB1PeriphClockCmd(RCC_APB1Periph_TIM2,ENABLE);
//2.选择时基单元的时钟(定时器上电后默认就是使用内部时钟,若不调用这个函数,那也是使用的内部时钟) TIM_InternalClockConfig(TIM2);//选择内部时钟
//3.配置时基单元TIM_TimeBaseInitTypeDef TIM_TimeBaseInitStructure;TIM_TimeBaseInitStructure.TIM_ClockDivision=TIM_CKD_DIV1;//选择1分频TIM_TimeBaseInitStructure.TIM_CounterMode=TIM_CounterMode_Up;//选择向上计数模式//若想定时1s,定时频率=72M/(PSC+1)/(ARR+1),预分频器和计数器都有1个数的偏差,所以要-1TIM_TimeBaseInitStructure.TIM_Period=10000-1;//ARR自动重装的值TIM_TimeBaseInitStructure.TIM_Prescaler=7200-1;//预分频器的值TIM_TimeBaseInitStructure.TIM_RepetitionCounter=0;//重复计数器,是高级定时器才有的TIM_TimeBaseInit(TIM2,&TIM_TimeBaseInitStructure);TIM_ClearFlag(TIM2,TIM_FLAG_Update);//手动把更新中断标志位清除一下,避免刚初始化完就进入中断//4.使能更新中断TIM_ITConfig(TIM2,TIM_IT_Update,ENABLE);
//5.配置NVIC NVIC_PriorityGroupConfig(NVIC_PriorityGroup_2);//优先级分组NVIC_InitTypeDef NVIC_InitStructure;NVIC_InitStructure.NVIC_IRQChannel=TIM2_IRQn;//选择定时器TIM2在NVIC里的通道NVIC_InitStructure.NVIC_IRQChannelCmd=ENABLE;NVIC_InitStructure.NVIC_IRQChannelPreemptionPriority=2;//抢占优先级NVIC_InitStructure.NVIC_IRQChannelSubPriority=1;//响应优先级NVIC_Init(&NVIC_InitStructure);
//6.启动定时器TIM_Cmd(TIM2,ENABLE);
}2.4.2 Timer.c
#ifndef __TIMER_H_
#define __TIMER_H_void Timer_Init(void);#endif2.4.3 main.c
#include "stm32f10x.h" // Device header
#include "TIMER.H"uint16_t Num;
int main(void)
{OLED_Init();Timer_Init();OLED_ShowString(1,1,"Num:");while(1){OLED_ShowNum(1,5,Num,5);}
}void TIM2_IRQHandler(void)//定时器2的中断函数
{if(TIM_GetITStatus(TIM2,TIM_IT_Update)==SET)//检查中断标志位{Num++;TIM_ClearITPendingBit(TIM2,TIM_IT_Update);//清除标志位}
}相关文章:

STM:TIM定时器——定时中断
文章目录 1、TIM定时器1.1定时器类型1.2定时中断的基本结构 2 定时器初始化2.2 初始化定时器的步骤2.3 TIM库函数2.4 配置TIM2.4.1 Timer.c2.4.2 Timer.c2.4.3 main.c 1、TIM定时器 定时器的功能可以对输入的时钟进行计数,并在计数值达到设定值时触发中断。 他包含…...
jetson tx2 nx实现在ros1中yolov5实现
亲测用以下链接实现功能。 安装ros。Ubuntu18.04安装ROS Melodic(详细,亲测安装完成,有清晰的截图步骤)_ubuntu 18 ros melodic-CSDN博客文章浏览阅读10w次,点赞835次,收藏3.8k次。这也是我在ubuntu里面安…...

【SpringBoot笔记43】SpringBoot应用程序集成spring-boot-admin监控工具
这篇文章,主要介绍SpringBoot应用程序如何集成spring-boot-admin监控工具。 目录 一、spring-boot-admin监控工具 1.1、创建admin-client客户端 (1)引入依赖...
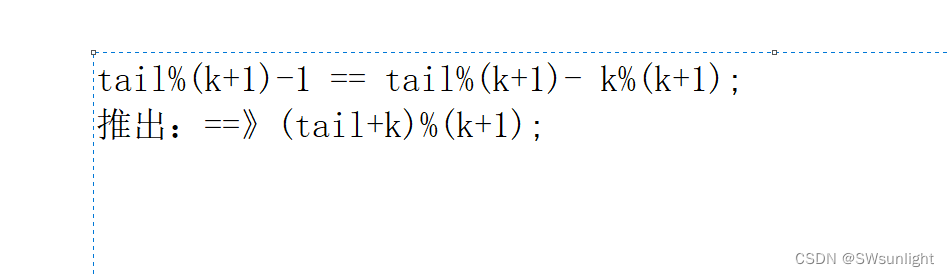
与队列和栈相关的【OJ题】
✨✨✨专栏:数据结构 🧑🎓个人主页:SWsunlight 目录 一、用队列实现栈: 1、2个队列的关联起来怎么由先进先出转变为先进后出:(核心) 2、认识各个函数干嘛用的: …...

Unity编辑器扩展
Unity编辑器扩展是指为Unity引擎开发者提供的一种扩展功能,可以增强Unity编辑器的功能和效能。这些扩展可以帮助开发者提高工作效率,简化工作流程,并提供更好的用户体验。本文将介绍Unity编辑器扩展的基本概念、开发流程以及一些常见的应用示…...
)
【kettle】kettle访问数据库系列文章及视频地址(更新中)
1.一直以来想写下基于kettle的系列文章,作为较火的数据ETL工具,也是日常项目开发中常用的一款工具,最近刚好挤时间梳理、总结下这块儿的知识体系。 2.这里整理了kettle访问数据库系列文章及视频地址整体链接,并及时补充、更新相关…...

共赴科技盛会“2024南京智博会”11月在南京国际博览中心召开
2024年,南京这座历史悠久的文化名城迎来了一场科技与智慧交织的盛会——南京智博会|南京国际智慧城市、物联网、大数据。本次博览会以智慧城市、人工智能、消费电子、物联网、大数据为主题,汇聚了全球各地的智能科技精英,共同探讨智慧城市建设…...
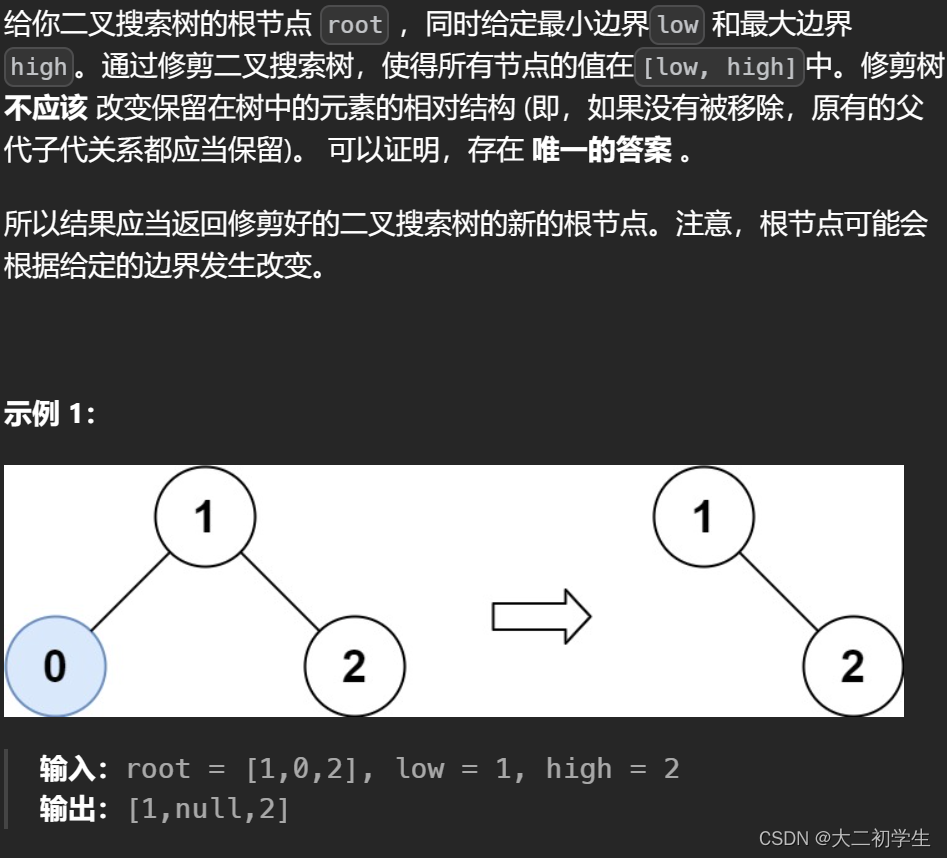
刷代码随想录有感(62):修建二叉搜索树
题干: 代码: class Solution { public:TreeNode* traversal(TreeNode* root, int low, int high){if(root NULL)return NULL;if(root->val < low)return traversal(root->right, low, high);if(root->val > high)return traversal(ro…...
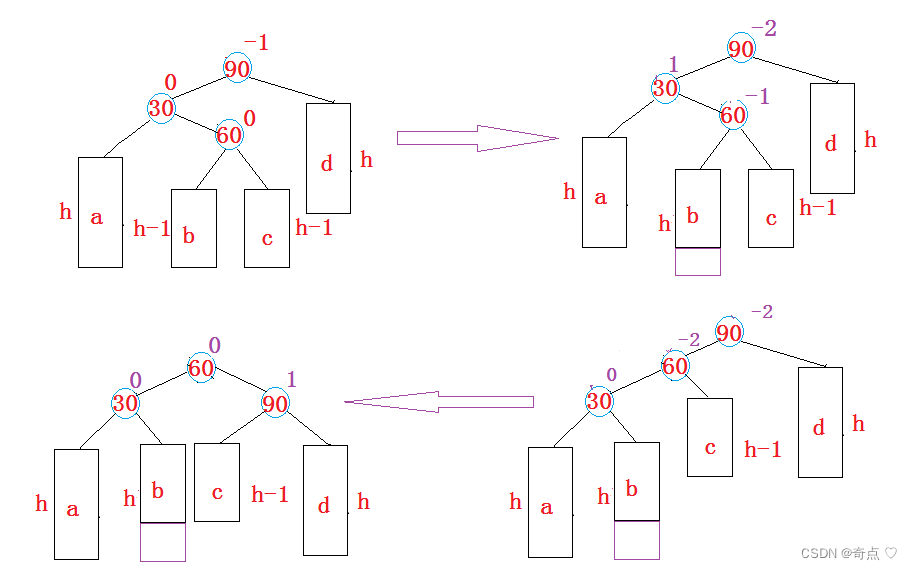
AVL树的旋转
目录 1.平衡因子 2.旋转 a.节点定义 b.插入 插入 平衡因子更新 旋转 左单旋 右单旋 右左双旋 左右双旋 3.AVL树的验证 1.平衡因子 我们知道搜索二叉树有缺陷,就是不平衡,比如下面的树 什么是搜索树的平衡?就是每个节点的左右子树的…...
)
C++(动态规划之拆分整数)
其实我交上去都有点似懂非懂 题目:(343. 整数拆分 - 力扣(LeetCode)) 给定一个正整数 n ,将其拆分为 k 个 正整数 的和( k > 2 ),并使这些整数的乘积最大化。 返回 …...

unix C之环境变量
什么是环境变量 每个进程都有自己的一张环境变量表,表中的每个条目都是形如 keyvalue 的键值对形式的环境变量。 进程可以通过环境变量访问计算机资源。 在终端下输入env命令,可以查看环境变量列表。 通过echo $name 可以查看某个环境变量的值。 环…...

Flutter实战记录-协作开发遇到的问题
一.前言 Android项目使用了混合架构,部分模块使用Flutter进行开发。在电脑A上开发的项目提交到git仓库,电脑B拉取后进行操作,遇到两个问题,特此做一下记录; 二.问题A Settings file ‘D:\xxx\settings.gradle’ line…...

Linux 安装JDK和Idea
安装JDK 下载安装包 下载地址: Java Downloads | Oracle (1) 使用xshell 上传JDK到虚拟机 (2) 移动JDK 包到/opt/environment cd ~ cd /opt sudo mkdir environment # 在 /opt下创建一个environment文件夹 ls# 复制JDK包dao /opt/environment下 cd 下载 ls jd…...

c#绘制渐变色的Led
项目场景: c#绘制渐变色的button using System; using System.ComponentModel; using System.Drawing; using System.Drawing.Drawing2D; using System.Windows.Forms; using static System.Windows.Forms.AxHost;namespace WindowsFormsApp2 {public class Gradie…...
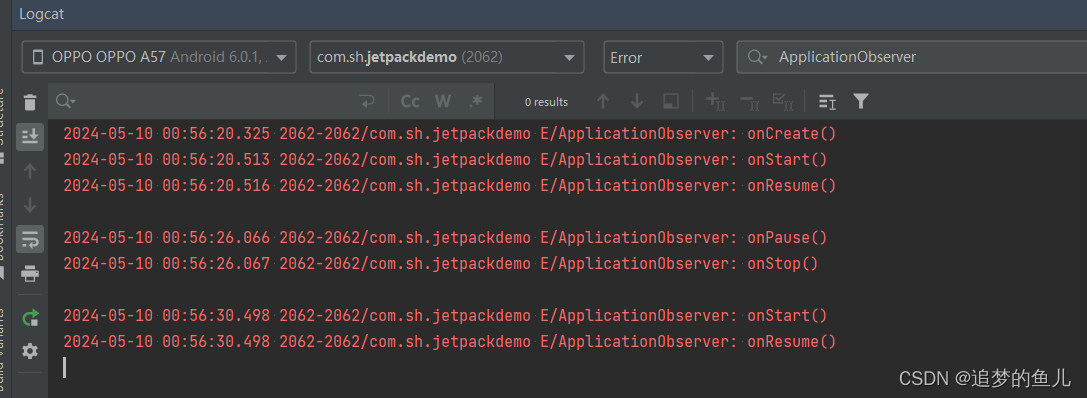
LifeCycle之ProcessLifeCycleOwner
问题:想要知道应用程序当前处在前台、后台、或从后台回到前台,想要知道应用的状态, LifeCycle提供了ProcessLifeCycleOwner的类,方便我们知道整个应用程序的生命周期情况 ProcessLifeCycleOwner 使用方法 1.首先添加依赖 imple…...

C++ | Leetcode C++题解之第79题单词搜索
题目: 题解: class Solution { public:bool exist(vector<vector<char>>& board, string word) {rows board.size();cols board[0].size();for(int i 0; i < rows; i) {for(int j 0; j < cols; j) {if (dfs(board, word, i, …...

如何通过PHP语言实现远程控制空调
如何通过PHP语言实现远程控制空调呢? 本文描述了使用PHP语言调用HTTP接口,实现控制空调,通过不同规格的通断器,来控制不同功率的空调的电源。 可选用产品:可根据实际场景需求,选择对应的规格 序号设备名称…...

【AI+换脸换装】从OpenAI 探索色情露骨内容领域浅聊AI换脸换装
5月9日消息,据外电报道,OpenAI 周三发布了文档草案,阐述了它希望 ChatGPT 及其其他人工智能技术如何运作。冗长的Model Spec 文件的一部分透露,该公司正在探索进军色情和其他露骨内容领域。 看完这个,心里有点惊讶&am…...
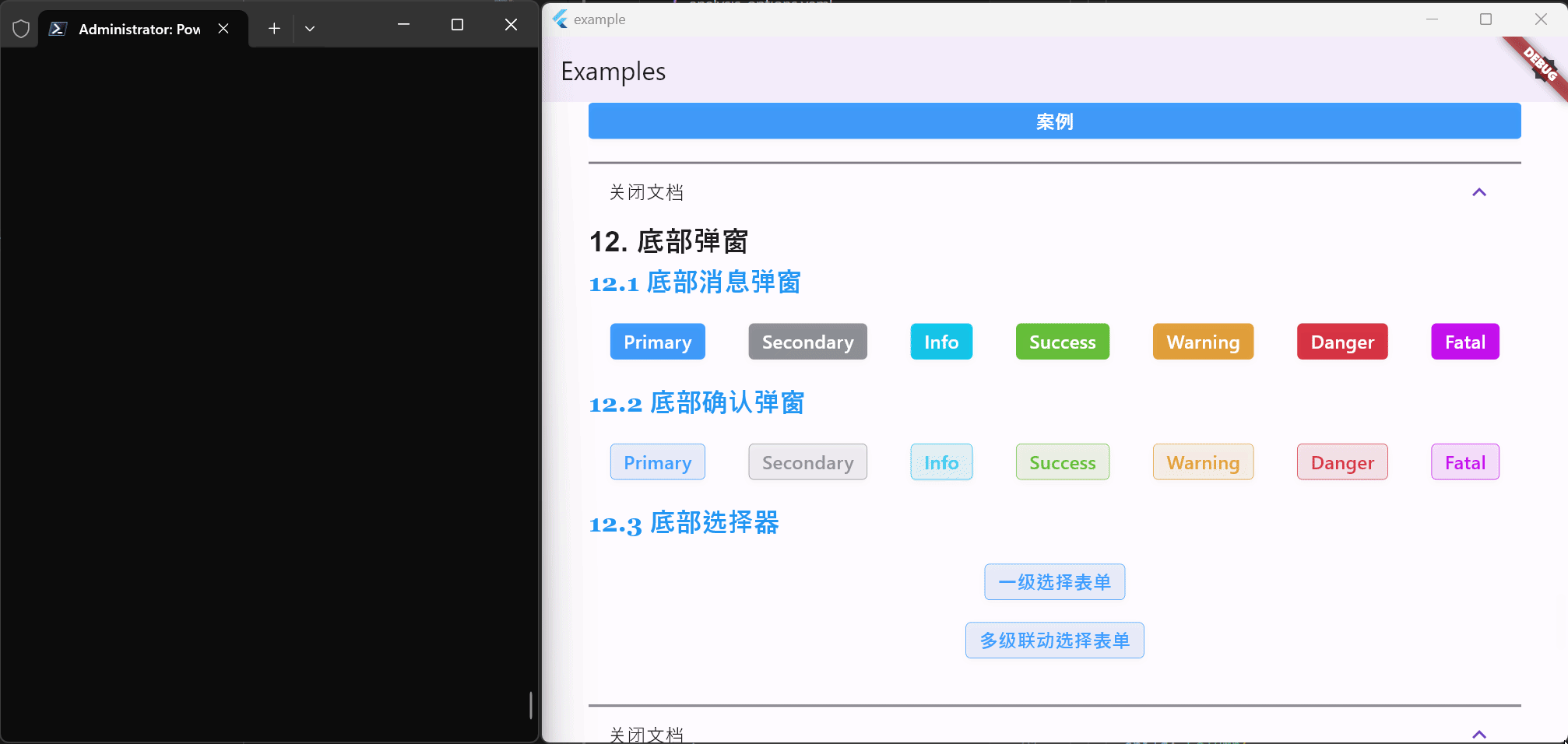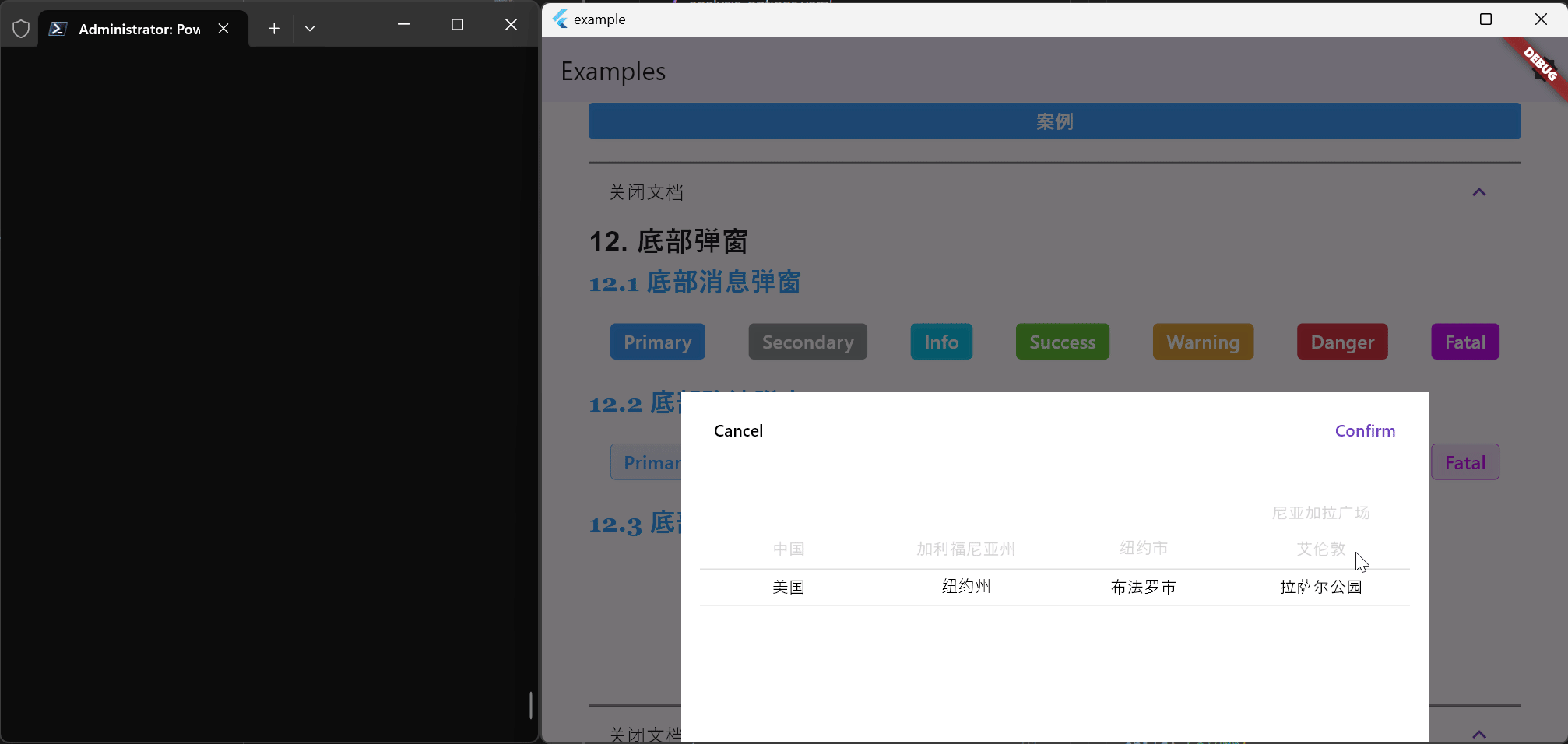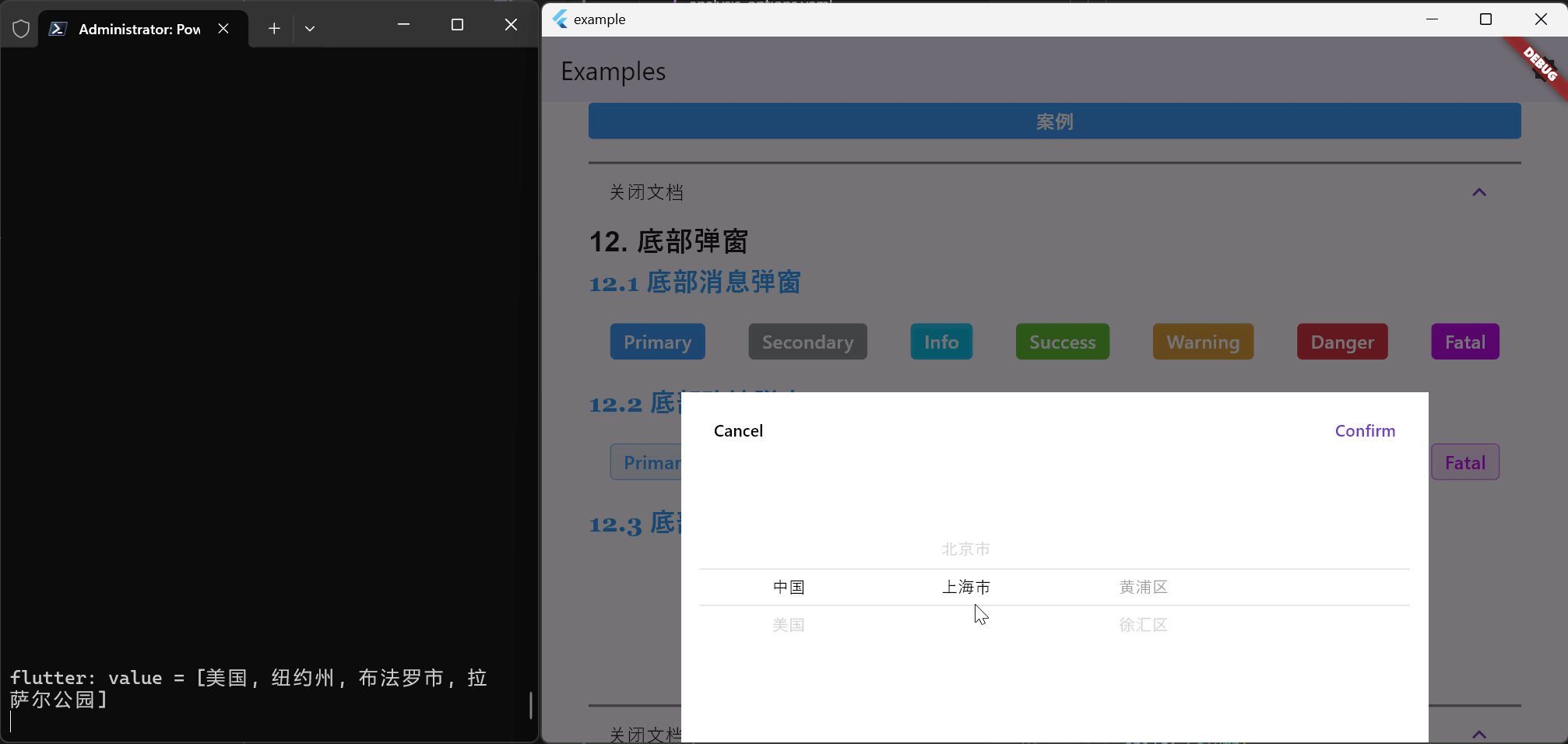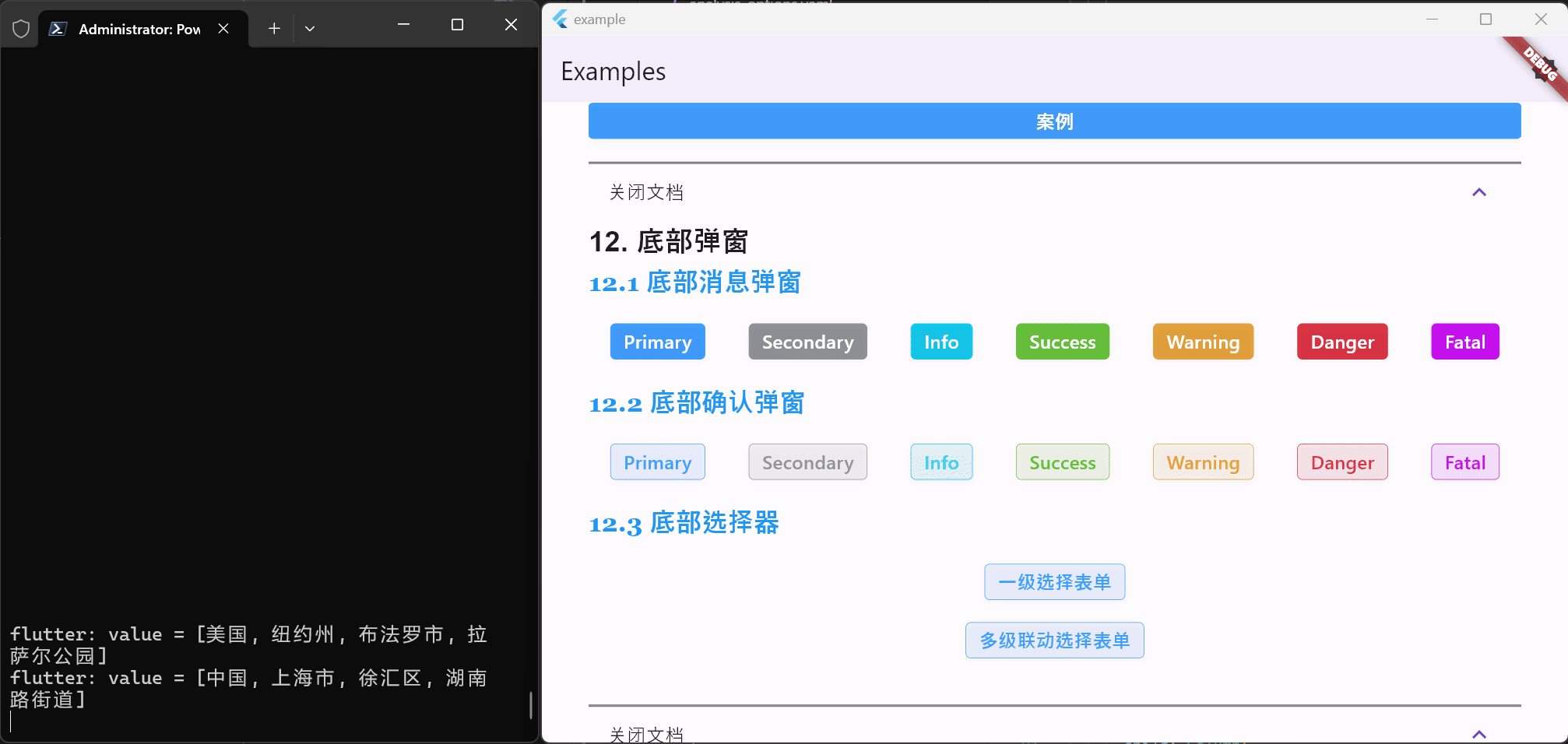
Flutter笔记:Widgets Easier组件库(13)- 使用底部弹窗
Flutter笔记 Widgets Easier组件库(13)使用底部弹窗 - 文章信息 - Author: 李俊才 (jcLee95) Visit me at CSDN: https://jclee95.blog.csdn.netMy WebSite:http://thispage.tech/Email: 291148484163.com. Shenzhen ChinaAddress of this …...
RobbitMQ基本消息队列的消息发送过程
RabbitMQ: One broker to queue them all | RabbitMQ RabbitMQ官网 SpringAmqp的官方地址:Spring AMQP 代码示例:对着代码看应该能看明白 publisher:消息发送者的代码示例 package cn.itcast.mq.helloworld;import com.rabbitmq.client.Channel; import com.rabb…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...

为什么要创建 Vue 实例
核心原因:Vue 需要一个「控制中心」来驱动整个应用 你可以把 Vue 实例想象成你应用的**「大脑」或「引擎」。它负责协调模板、数据、逻辑和行为,将它们变成一个活的、可交互的应用**。没有这个实例,你的代码只是一堆静态的 HTML、JavaScript 变量和函数,无法「活」起来。 …...

BLEU评分:机器翻译质量评估的黄金标准
BLEU评分:机器翻译质量评估的黄金标准 1. 引言 在自然语言处理(NLP)领域,衡量一个机器翻译模型的性能至关重要。BLEU (Bilingual Evaluation Understudy) 作为一种自动化评估指标,自2002年由IBM的Kishore Papineni等人提出以来,…...

WebRTC从入门到实践 - 零基础教程
WebRTC从入门到实践 - 零基础教程 目录 WebRTC简介 基础概念 工作原理 开发环境搭建 基础实践 三个实战案例 常见问题解答 1. WebRTC简介 1.1 什么是WebRTC? WebRTC(Web Real-Time Communication)是一个支持网页浏览器进行实时语音…...

Chrome 浏览器前端与客户端双向通信实战
Chrome 前端(即页面 JS / Web UI)与客户端(C 后端)的交互机制,是 Chromium 架构中非常核心的一环。下面我将按常见场景,从通道、流程、技术栈几个角度做一套完整的分析,特别适合你这种在分析和改…...
