贪心算法-活动选择问题背包问题
目录
活动选择问题
无重叠区间-Leetcode 435
分数背包问题--贪心解法
贪心法
0-1 背包问题
贪心法
贪心算法的局限
Set cover problem
活动选择问题
分析:
/* 要在一个会议室举办n个活动 - 每个活动有它们各自的起始和结束时间 - 找出在时间上互不冲突的活动组合,能够最充分利用会议室(举办的活动次数最多)例10 1 2 3 4 5 6 7 8 9|--------) |--------)|--------)选1 3 能够举办2个活动例20 1 2 3 4 5 6 7 8 9|---)|---)|-----------------------)|-------)|---)|---------------)4个活动几种贪心策略1.优先选择持续时间最短的活动 以下情形不满足方案out0 1 2 3 4 5 6 7 8 9|---------------)|-------)|----------------)\2.优先选择冲突最少的活动编号 0 1 2 3 4 5 6 7 8 91 |-------) 3 选中2 |-------) 43 |-------) 44 |-------) 45 |-------) 46 |-------) 2 选中7 |------------) 48 |--------) 49 |--------) 410 |--------) 411 |-------) 3 选中但实际上应该是1 5 7 11 所以这个也不行3. 优先选择最先开始的活动 不行0 1 2 3 4 5 6 7 8 9|-----------------------------------)|---)|---)|---)4. 优先选择最先结束的活动*/
import java.util.ArrayList;
import java.util.Arrays;
import java.util.Comparator;
import java.util.List;/*** <h1>活动选择问题 - 贪心解法</h1>* Leetcode 435 无重叠区间本质就是活动选择问题*/
public class ActivitySelectionProblem {static class Activity{int index;int start;int finish;public Activity(int index,int start,int finish){this.index = index;this.start = start;this.finish = finish;}public int getFinish(){return finish;}@Overridepublic String toString(){return "Activity("+index+")";}}public static void main(String[] args) {Activity[] activities = new Activity[]{new Activity(0, 1, 3),new Activity(1, 2, 4),new Activity(2, 3, 5)};
// Activity[] activities = new Activity[]{
// new Activity(0, 1, 2),
// new Activity(1, 3, 4),
// new Activity(2, 0, 6),
// new Activity(3, 5, 7),
// new Activity(4, 8, 9),
// new Activity(5, 5, 9)
// };Arrays.sort(activities, Comparator.comparingInt(Activity::getFinish));System.out.println(Arrays.toString(activities));select(activities, activities.length);}public static void select(Activity[] activities, int length) {List<Activity>result = new ArrayList<>();Activity prev = activities[0];result.add(prev);for(int i = 1;i<length;i++){Activity curr = activities[i]; //当前正在处理的活动if (curr.start >= prev.finish) {result.add(curr);prev = curr;}}for (Activity activity : result) {System.out.println(activity);}}
}
435. 无重叠区间 - 力扣(LeetCode)
无重叠区间-Leetcode 435
| 题目编号 | 题目标题 | 算法思路 |
|---|---|---|
| 435 | 无重叠区间 | 贪心 |
class Solution {public int eraseOverlapIntervals(int[][] intervals) {if(intervals.length==0){return 0;}Arrays.sort(intervals,Comparator.comparingInt(a->a[1]));int i,j;i=0;int count =1;for(j = 1;j<intervals.length;j++){if(intervals[j][0] >= intervals[i][1]){i = j;count++;}}return intervals.length-count;}
}-
找到不重叠的最多的活动数(count),即活动选择问题原始需求
-
在此基础上,活动总数 - count,就是题目要的排除数量
分数背包问题--贪心解法
贪心法
/* 1. n个物品都是液体,有重量和价值 2. 现在你要取走 10升 的液体 3. 每次可以不拿,全拿,或拿一部分,问最高价值是多少编号 重量(升) 价值0 4 24 水1 8 160 牛奶 选中 7/82 2 4000 五粮液 选中3 6 108 可乐4 1 4000 茅台 选中8140简化起见,给出的数据都是【价值/重量】能够整除,避免计算结果中出现小数,增加心算难度*/
import java.util.Arrays;
import java.util.Comparator;public class FractionalKnapsackProblem {static class Item {int index;int weight;int value;public Item(int index, int weight, int value) {this.index = index;this.weight = weight;this.value = value;}public int unitPrice() {return value / weight;}@Overridepublic String toString() {return "Item(" + index + ")";}}public static void main(String[] args) {Item[] items = new Item[]{new Item(0, 4, 24),new Item(1, 8, 160),new Item(2, 2, 4000),new Item(3, 6, 108),new Item(4, 1, 4000),};select(items, 10);}static void select(Item[] items, int total) {Arrays.sort(items, Comparator.comparingInt(Item::unitPrice).reversed());//reversed()降序int remainder = total;int max = 0;for (Item item : items) {if (remainder - item.weight >= 0) {//一次能够拿完max += item.value;remainder -= item.weight;} else {//拿不完max += remainder * item.unitPrice();break;}}System.out.println("最高价值为:" + max);}}0-1 背包问题
贪心法
可能得不到最优解
/*0-1 背包问题1. n个物品都是固体,有重量和价值2. 现在你要取走不超过 10克 的物品3. 每次可以不拿或全拿,问最高价值是多少编号 重量(g) 价值(元)0 1 1_000_000 钻戒一枚 选中1 4 1600 黄金一块 4002 8 2400 红宝石戒指一枚 3003 5 30 白银一块按照分数背包问题解法: 1001630 但其实不对 应该是1002400*/
import java.util.Arrays;
import java.util.Comparator;public class KnapsackProblem {static class Item {int index;int weight;int value;public Item(int index, int weight, int value) {this.index = index;this.weight = weight;this.value = value;}public int unitValue() {return value / weight;}@Overridepublic String toString() {return "Item(" + index + ")";}}public static void main(String[] args) {Item[] items = new Item[]{new Item(0, 1, 1_000_000),new Item(1, 4, 1600),new Item(2, 8, 2400),new Item(3, 5, 30)};select(items, 10);}static void select(Item[] items, int total) {Arrays.sort(items, Comparator.comparingInt(Item::unitValue).reversed());int max = 0; // 最大价值for (Item item : items) {System.out.println(item);if (total >= item.weight) { // 可以拿完total -= item.weight;max += item.value;} else { // 拿不完
// max += total * item.unitValue();
// break;}}System.out.println("最大价值是:" + max);}
}贪心算法的局限
| 问题名称 | 是否能用贪心得到最优解 | 替换解法 |
|---|---|---|
| Dijkstra(不存在负边) | ✔️ | |
| Dijkstra(存在负边) | ❌ | Bellman-Ford |
| Prim | ✔️ | |
| Kruskal | ✔️ | |
| 零钱兑换 | ❌ | 动态规划 |
| Huffman 树 | ✔️ | |
| 活动选择问题 | ✔️ | |
| 分数背包问题 | ✔️ | |
| 0-1 背包问题 | ❌ | 动态规划 |
Set cover problem
集合覆盖问题
这个问题后面会出文章! 敬请期待!
相关文章:

贪心算法-活动选择问题背包问题
目录 活动选择问题 无重叠区间-Leetcode 435 分数背包问题--贪心解法 贪心法 0-1 背包问题 贪心法 贪心算法的局限 Set cover problem 活动选择问题 分析: /* 要在一个会议室举办n个活动 - 每个活动有它们各自的起始和结束时间 - 找出在时间上互不冲突的活动组合,能…...

Web3工具集合 - 00
使用 React 和 Material-UI 构建的 Web3 工具集合 大家好! 我很高兴向大家介绍我最近刚启动了一个项目:Web3 工具集合。 这个项目的目的是一个集成各种 Web3 工具的网站,旨在为开发人员和加密货币爱好者提供便捷的工具和资源。 特点&#…...
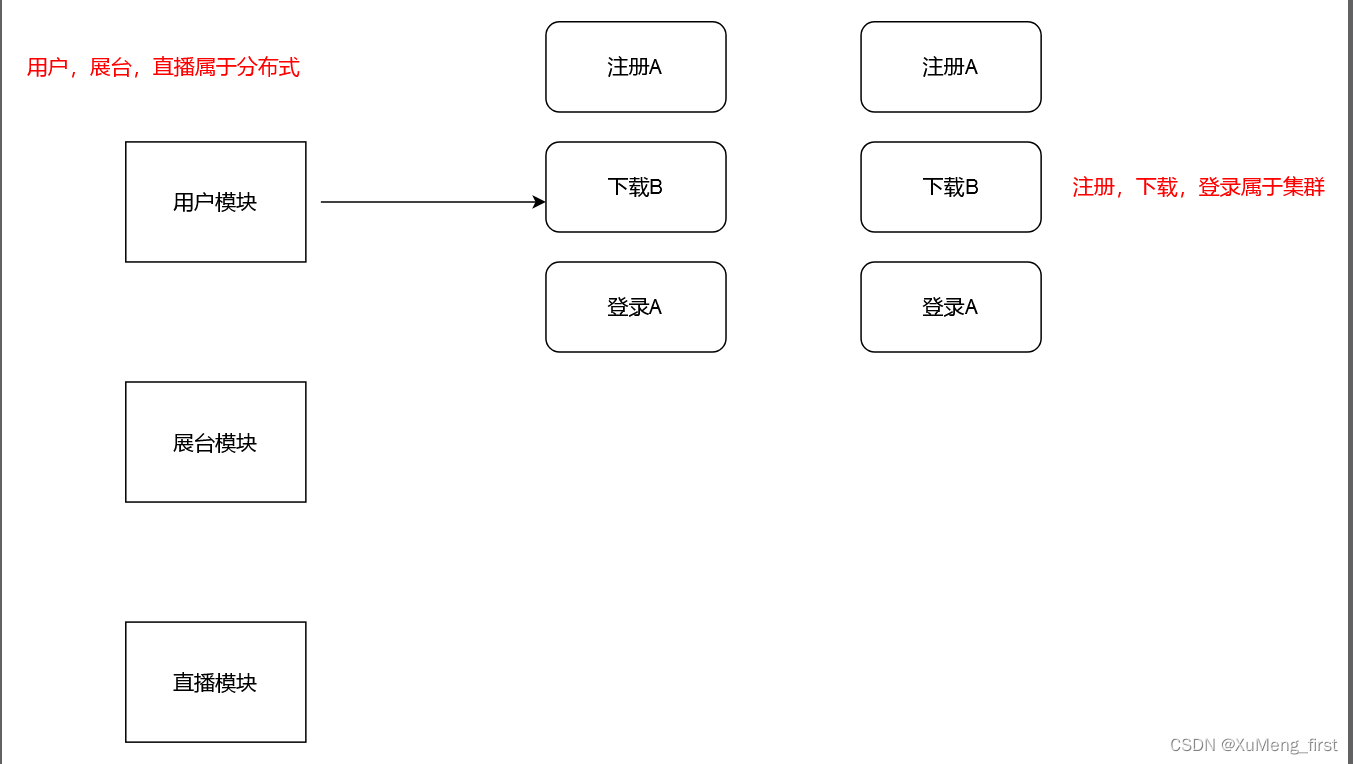
分布式与集群的区别
先说区别: 分布式是并联工作的,集群是串联工作的。 分布式中的每一个节点都可以做集群。而集群并不一定就是分布式的。 集群举例:比如新浪网,访问的人很多,他可以做一个集群,前面放一个相应的服务器&…...

学习心得:如何开始学习一款MCU
一、MCU简介 任何一款MCU,其基本原理和功能都是大同小异,所不同的只是其外围功能模块的配置及数量、指令系统等。对于指令系统,虽然形式上看似千差万别,但实际上只是符号的不同,其所代表的含义、所要完成的功能和寻址…...
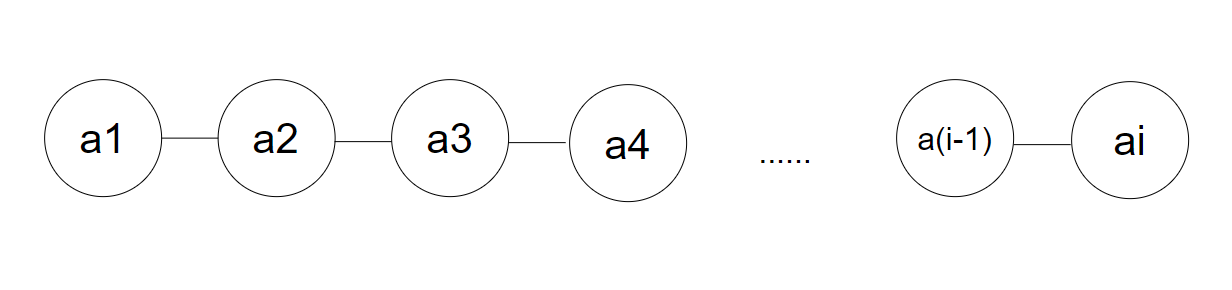
顺序表的实现(迈入数据结构的大门)(1)
上一节我们认识到了什么是数据结构 这一节我们就来实现第一个数据结构的实现 思考一个问题: 假定一个数组,空间为10,已经使用了5个,向其中插入数据的步骤: 1.插入数据,我们先要求数组长度,其…...
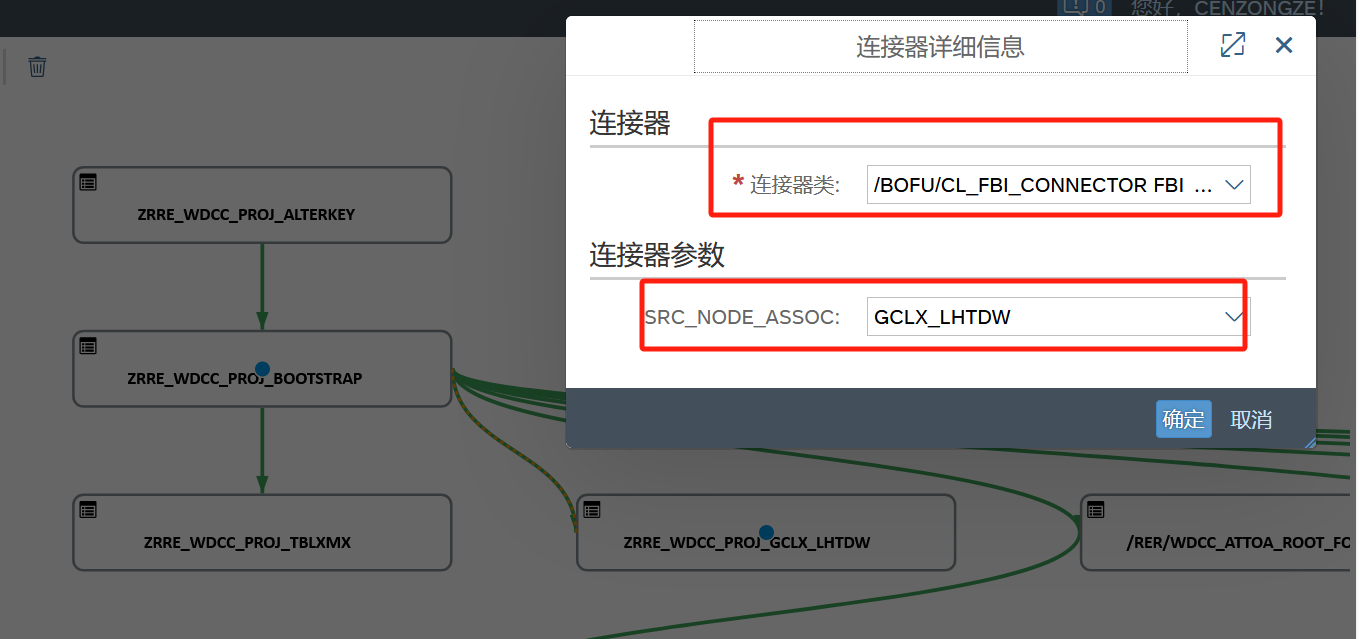
RERCS系统-WDA+BOPF框架实战例子 PART 1-新建List UIBB(列表组件)并分配Feeder Class和Node Element
需求背景: 已有的项目主数据功能,新增一个列表UIBB显示主数据额外的关联数据明细。 1、Fiori页面通过右键-技术帮助打开对应的组件配置; 2、双击对应的组件配置,调整对应的页面新建UIBB; 3、填写对应的UIBB属性字段&a…...

如何从 iPhone 恢复已删除或丢失的联系人?
不小心删除了您的 iPhone 联系人?不用担心。我们将向您展示如何从 iPhone或 iPad恢复已删除或丢失的联系人。当您从 iPhone 中删除联系人时,您可能认为无法将其恢复。但事实是,您可以从 iPhone 或 iPad 恢复已删除的联系人,因为它…...

RISCV 外部GCC 工具链安装@FreeBSD15
在交叉编译的时候,可以使用FreeBSD15默认的工具链:LLVM 也可以使用GCC工具链,GCC可以使用现成pkg包安装,也可以编译安装。 LLVM的特点是高移植性和高效,但学习成本高。GCC的特点是成熟稳定,但优化能力有限…...

全栈开发之路——前端篇(9)插槽、常用api和全局api
全栈开发一条龙——前端篇 第一篇:框架确定、ide设置与项目创建 第二篇:介绍项目文件意义、组件结构与导入以及setup的引入。 第三篇:setup语法,设置响应式数据。 第四篇:数据绑定、计算属性和watch监视 第五篇 : 组件…...

减瘦误区、雷点、陷阱和挑战怎么应对
在减瘦过程中,很多肥胖人群都容易踩到坑。比如陷入误区,认为只有短期快速的减调方式方法,才值得尝试,而忽视身体健康;或是踩到雷点,轻信强速方剂或方法,结果身体产生了排斥或根本没效用白花钱&a…...

Leetcode—946. 验证栈序列【中等】
2024每日刷题(133) Leetcode—946. 验证栈序列 实现代码 class Solution { public:bool validateStackSequences(vector<int>& pushed, vector<int>& popped) {int left 0;for(int i 0; i < popped.size(); i) {while(left &…...

Selenium定位方法及代码
天行健,君子以自强不息;地势坤,君子以厚德载物。 每个人都有惰性,但不断学习是好好生活的根本,共勉! 文章均为学习整理笔记,分享记录为主,如有错误请指正,共同学习进步。…...

GitHub搭建免费博客
一、GitHub仓库准备 搭建博客需要准备两个仓库。一个存放博客图床的仓库,另一个存放博客网站的仓库。 1.1、图床创建 新建仓库 第一步: 第二步: 生成Token令牌 点击右上角头像->Settings->下拉,直到左侧到底&#…...
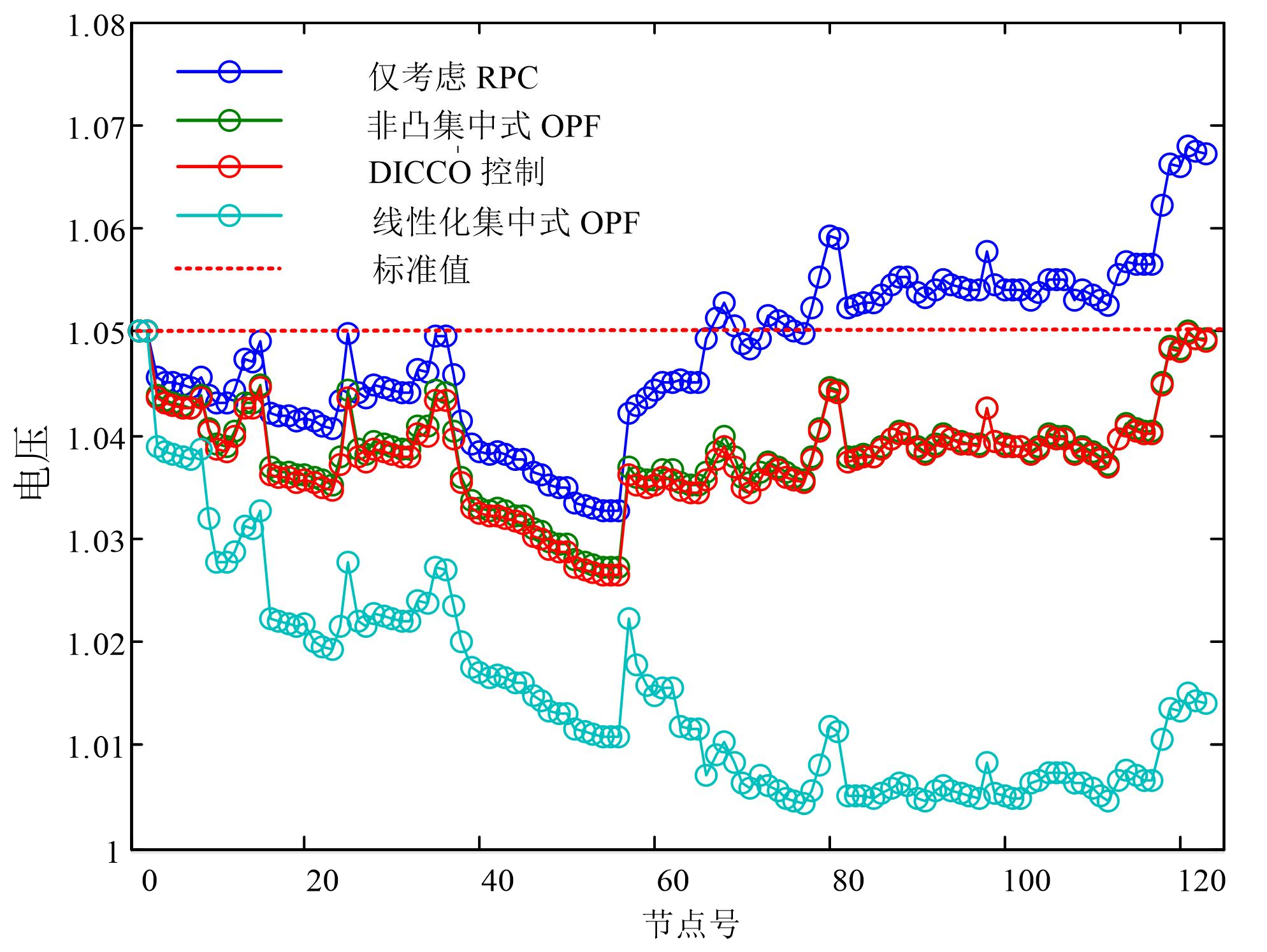
开源代码分享(28)-含分布式光伏的配电网集群划分和集群电压协调控制
参考文献: [1] Chai Y , Guo L , Wang C ,et al.Network Partition and Voltage Coordination Control for Distribution Networks With High Penetration of Distributed PV Units[J].IEEE Transactions on Power Systems, 2018:3396-3407.DOI:10.1109/TPWRS.2018…...
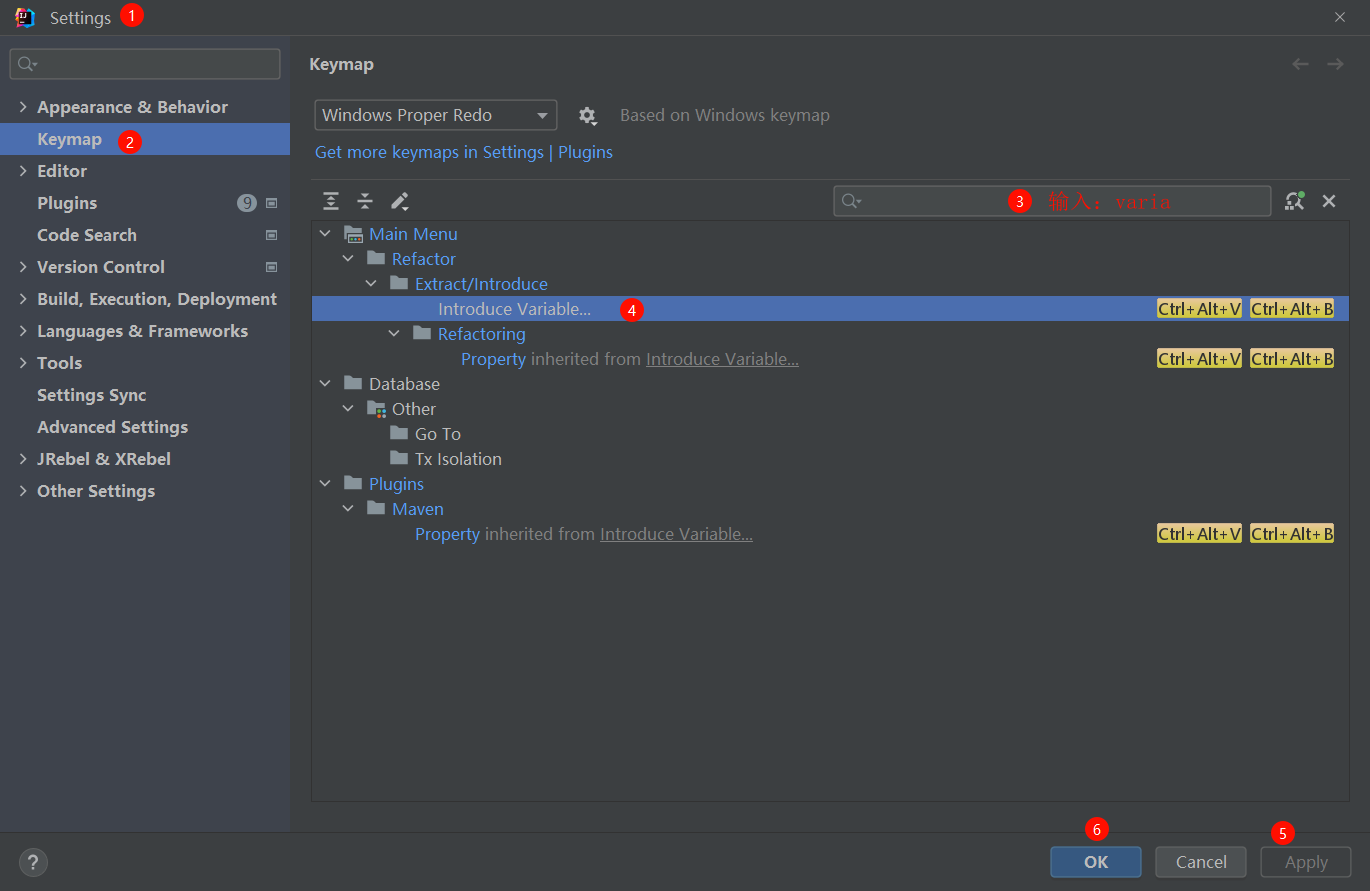
idea-自我快捷键-2
1. 书签 创建书签: 创建书签:F11创建特色标记书签:Ctrl F11快速添加助记符书签:ctrl shift 数字键 查看书签: shift F11快速定位到助记符书签:Ctrl 数字键 删除书签: delete 2. 自动…...
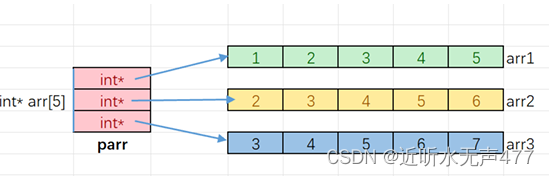
深入学习指针3
目录 前言 1.二级指针 2.指针数组 3.指针数组模拟二维数组 前言 Hello,小伙伴们我又来了,上期我们讲到了数组名的理解,指针与数组的关系等知识,那今天我们就继续深入到学习指针域数组的练联系,如果喜欢作者菌生产的内容还望不…...

礼赞劳动节,致敬劳动者。节日随想:疾笔耕耘也是一种劳动方式。
马克思也快诞辰了206年了,恩格斯领导的第二国际通过的决议节日也迎来了134岁的生日了,我也继续在劳动的路上。 五月是值得纪念的日子,作为一名无上光荣的分子,无比仰慕崇拜的两位先驱前辈大胡子,其一 生于斯࿰…...

学习Java的日子 Day45 HTML常用的标签
Day45 HTML 1.掌握常用的标签 1.1 标题标签 h1-h6 <h1>一级标签</h1> <h2>二级标签</h2> <h3>三级标签</h3> <h4>四级标签</h4> <h5>五级标签</h5> <h6>六级标签</h6> 显示特点: * 文字…...

兔子与狮子
兔子与狮子 一只骨瘦如柴的兔子,在慢悠悠地吃草 趴在边上的狮子说,多吃点吧,你身上一点肉都没有 兔子说,我正在减肥,体重越来越轻,骨头越来越硬 狮子舔了舔嘴巴,你再狡猾,也是我的…...

GNU/Linux - 系统启动流程及rcS脚本介绍
Linux系统启动流程 在 Linux 系统启动过程中,会按特定顺序执行多个脚本和初始化例程,以使系统进入可用状态。虽然具体顺序可能因 Linux 发行版和版本而异,但以下是典型执行顺序的概括性概述: 1. BIOS/UEFI: 系统开机后…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

【Go语言基础【12】】指针:声明、取地址、解引用
文章目录 零、概述:指针 vs. 引用(类比其他语言)一、指针基础概念二、指针声明与初始化三、指针操作符1. &:取地址(拿到内存地址)2. *:解引用(拿到值) 四、空指针&am…...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...
