二叉树进阶 --- 中
目录
1. find 的递归实现
2. insert 的递归实现
3. erase 的递归实现
3.1. 被删除的节点右孩子为空
3.2. 被删除的节点左孩子为空
3.3. 被删除的节点左右孩子都不为空
4. 析构函数的实现
5. copy constructor的实现
6. 赋值运算符重载
7. 搜索二叉树的完整实现
1. find 的递归实现
find的递归实现较为简单,思路是:根据当前节点的 key 与传入的 key 作比较:
- 如果前者大于后者,那么当前节点往左子树走;
- 如果前者小于后者,那么当前节点往右子树走;
- 如果两者相等,返回true;
- 走到空,返回false。
代码实现:
// 对外提供的
bool find_recursion(const T& key)
{return _find_recursion(_root, key);
}
// 类中私有的
bool _find_recursion(Node* root, const T& key)
{if (root == nullptr)return false;else{if (root->_key < key)return _find_recursion(root->_right, key);else if (root->_key > key)return _find_recursion(root->_left, key);elsereturn true;}
}2. insert 的递归实现
insert分为两个过程
- 第一个过程:找到合适位置;
- 第二个过程:构建新节点,并完成连接关系。
假如现在我们已经得到了合适的插入位置,那么如何连接呢?
例如,如下图所示:我们要插入13这个数据,现在的关键问题是,如何将15和13这两个节点连接起来呢? 具体如下:
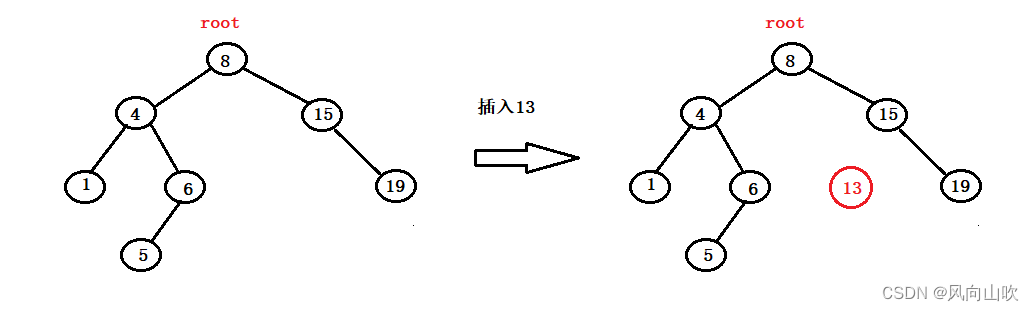
第一种方法:调用函数时,将父亲节点即这里的15也传进来。找到合适位置,创建节点并连接。
但是我们在这里提出一个较好玩的玩法,利用引用传参,如下所示:
// 对外提供的
bool insert_recursion(const T& key)
{ return _insert_recursion(_root, key);
}
// 类中私有的
bool _insert_recursion(Node*& root, const T& key)
{if (root == nullptr){// 走到空, 说明找到了目标位置, 需要构建新节点, 并完成连接关系// 在这里, 我们用上图解释:// root就是15这个节点的左孩子的引用,即root就是15的左孩子// 给root new了一个node(key),等价于插入了这个节点,并连接了起来.root = new Node(key);return true;}else{if (root->_key < key)return _insert_recursion(root->_right, key);else if (root->_key > key)return _insert_recursion(root->_left, key);elsereturn false;}
}3. erase 的递归实现
对于erase的递归实现,其实也可以分为两个过程:
- 第一个过程:找到这个要删除的特殊节点;
- 第二个过程:可以分为三种情况(左孩子为空、右孩子为空、左右孩子都不为空),根据不同情况进行删除。
假设我们现在已经得到了要删除节点的位置,该如何删除呢?
3.1. 被删除的节点右孩子为空
如图所示:我们要删除6号节点(其右孩子为空),该如何删除:
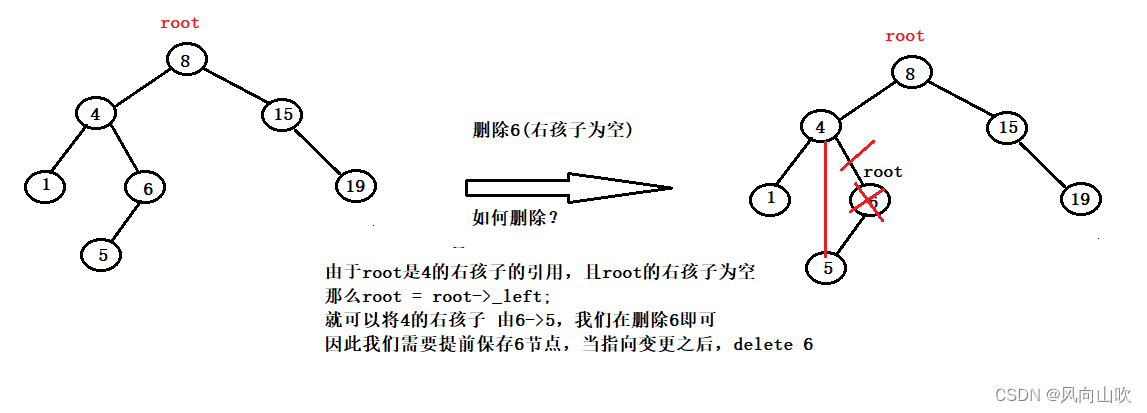
由于 root 是4的右孩子的引用,且 root 的右孩子为空,那么root = root->_left,就可以将4的右孩子由6变更为5,我们在删除6即可,因此我们需要提前保存6节点,当指向变更之后,delete 6。
3.2. 被删除的节点左孩子为空
如图所示:我们要删除15号节点(其左孩子为空),该如何删除:
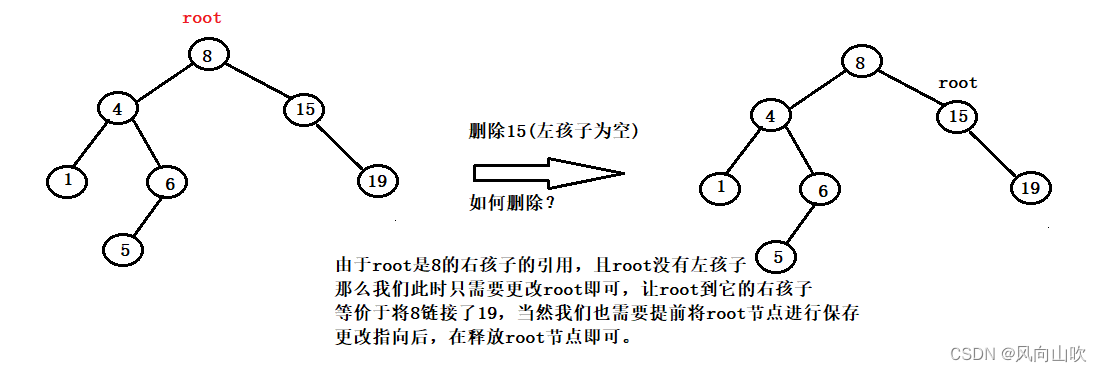
由于 root 是8的右孩子的引用,且 root 没有左孩子,那么我们此时只需要更改 root 即可,让 root 到它的右孩子 (root = root->_right),等价于将8连接了19,当然我们也需要提前将 root 节点进行保存,更改指向后,在释放 root 节点即可。
3.3. 被删除的节点左右孩子都不为空
较为复杂的就是第三种情况了,由于此时被删除节点有两个孩子,因此无法像上面两种情况进行处理。此时我们还是要利用循环实现的思路:
- (1):从被删除的节点开始,先找到左子树的最大节点or右子树的最小节点(我在这里称之为"合适节点");
- (2):交换这个"合适结点"和被删除节点的key;
- (3):将删除原节点转化为删除我们后找的这个"合适节点"。
在这里我们用实例说明,如下图所示:如果我要删除下图中的4,该如何删除?
我在这里实现的"合适节点"是: 左子树的最大(右)节点
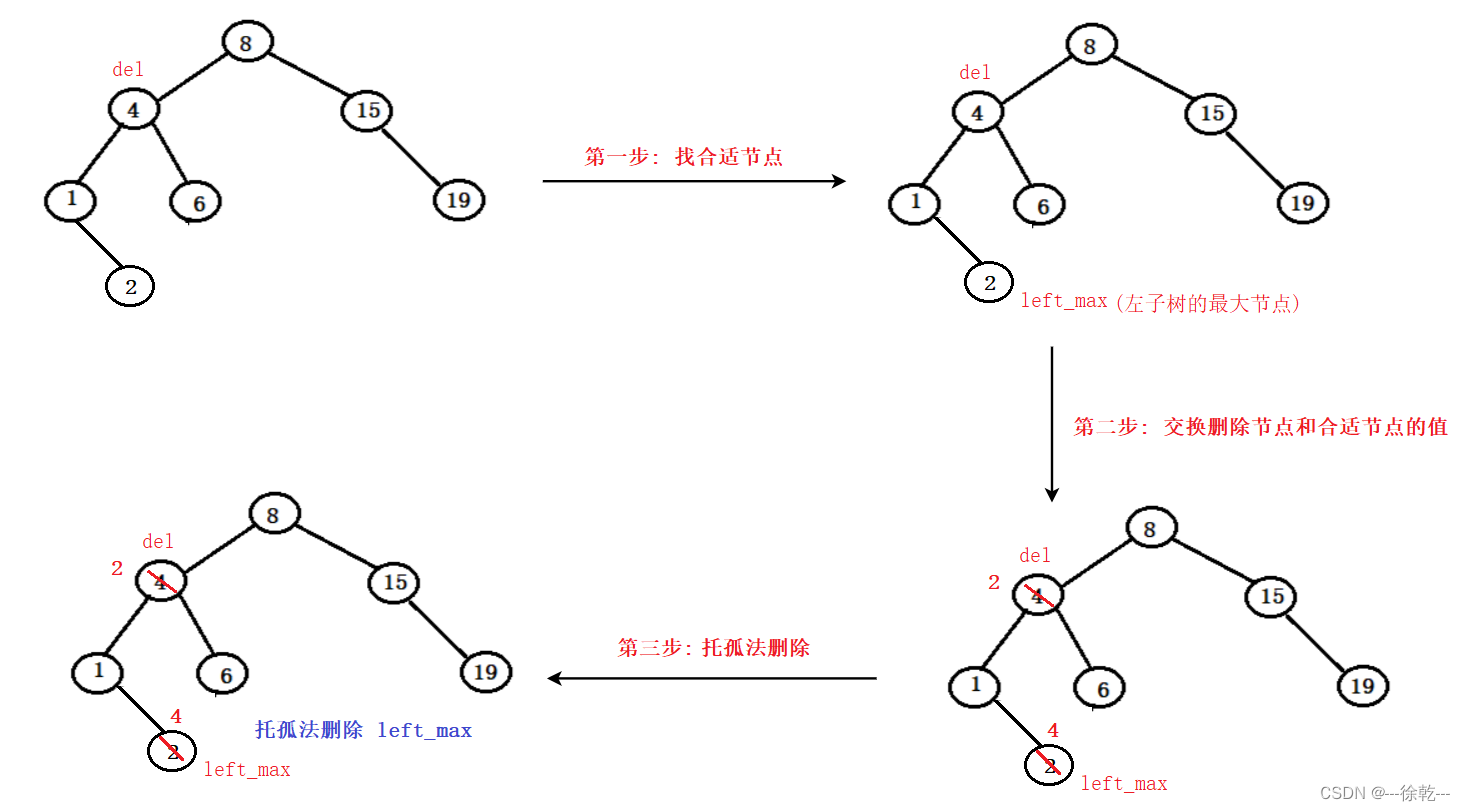
相信前两个过程是没有困难的,最后一步可能不好实现,但是当我们经过了前两个过程,我们发现被删除节点变成了我们找到的"合适节点",而且这个"合适节点"很有特征,如果它是左子树的最大值,那么它一定不会有右子树,反之,如果他是右子树的最小节点,那么它一定不会有左子树。因此我们可以在递归一次,如果"合适节点"是左子树的最大节点,那么我们递归树的左子树即可,反之如果是右子树的最小节点,那么我们递归树的右子树即可。
代码如下:
// 对外提供的
bool erase_recursion(const T& key)
{return _erase_recursion(_root, key);
}
// 类中私有的
bool _erase_recursion(Node*& root, const T& key)
{if (!root)return false;else{// 如果当前节点的key > 目标key,那么递归它的左子树即可if (root->_key > key)return _erase_recursion(root->_left, key);// 如果当前节点的key < 目标key,那么递归它的右子树即可else if (root->_key < key)return _erase_recursion(root->_right, key);// 如果找到了,进行删除else{// 此时的root就是要删除的节点Node* del = root;// a. 左子树为空if (root->_left == nullptr)root = root->_right;// b. 右子树为空else if (root->_right == nullptr)root = root->_left;// c. 左右子树都不为空else{// 左子树的最右节点Node* left_max = root->_left;while (left_max->_right)left_max = left_max->_right;// 交换"合适节点"和"被删除节点"的keystd::swap(left_max->_key, root->_key);// 在这里递归左子树即可return _erase_recursion(root->_left, key);}delete del;del = nullptr;return true;}}
}4. 析构函数的实现
析构函数的实现我们依据的是后序的思想(LRN),先析构左子树、然后是右子树、最后才是根。这种实现的原因是是少了许多的记录信息,例如在这里我们就不用记录下一个节点。因为我们释放的就是当前的叶子节点。
具体实现如下:
~BinarySearchTree()
{_BSTDestroy(_root);
}
// 注意我们这里传递的是根的引用
void _BSTDestroy(Node*& root)
{if (root == nullptr)return;else{// 依据后序的思想_BSTDestroy(root->_left);_BSTDestroy(root->_right);delete root;root = nullptr;}
}5. copy constructor的实现
老生常谈的问题,如果我们没有显示实现拷贝构造函数,那么编译器默认生成的拷贝构造会对内置类型按照字节序的方式进行拷贝,对自定义类型成员属性会去调用它的拷贝构造函数。而字节序的方式进行拷贝会带来两个问题:
- 其一,其中一个对象的修改会影响另一个对象;
- 其二,同一空间会被析构两次,进程crash。
因此,我们在这里必须要实现深拷贝,那如何实现呢?我们可以借助前序的思想(NLR)。从根节点开始进行构造节点,然后递归构造它的左子树和右子树。注意构造的时候需要它们的连接关系。
代码如下:
BinarySearchTree(const BinarySearchTree<T>& copy)
{_root = _creat_new_root(copy._root);
}
Node* _creat_new_root(Node* root)
{// 如果遇到空了,就不用构造了if (root == nullptr)return nullptr;else{// 根据前序的思想(NLR),依次构造它的根、左子树、右子树 // 同时将它们连接起来Node* new_root = new Node(root->_key);new_root->_left = _creat_new_root(root->_left);new_root->_right = _creat_new_root(root->_right);return new_root;}
}6. 赋值运算符重载
赋值运算符重载就比较简单了,因为我们已经实现了copy constructor,在这里利用传值传参会进行拷贝构造的特性实现我们的赋值
代码如下:
// 传值传参会进行拷贝构造
BinarySearchTree<T>& operator=(BinarySearchTree<T> copy)
{std::swap(_root, copy._root);return *this;
}7. 搜索二叉树的完整实现
代码如下:
#ifndef _BINARY_SEARCH_TREE_HPP_
#define _BINARY_SEARCH_TREE_HPP_#include <iostream>namespace Xq
{template<class T>struct BinarySearchTreeNode{BinarySearchTreeNode<T>* _left;BinarySearchTreeNode<T>* _right;T _key;BinarySearchTreeNode(const T& key) :_key(key), _left(nullptr), _right(nullptr) {}};template<class T>class BinarySearchTree{private:typedef BinarySearchTreeNode<T> Node;public:BinarySearchTree(Node* root = nullptr) :_root(root) {}bool insert(const T& key){// 1. 如果是空树,直接对_root赋值即可,插入成功并返回trueif (_root == nullptr){_root = new Node(key);return true;}else{// step 1: 先找目标位置Node* cur = _root;// 为了更好的连接新节点, 因此记录父节点Node* parent = nullptr;while (cur){// 如果当前节点的Key大于目标Key// 当前节点应该向左子树走if (cur->_key > key){parent = cur;cur = cur->_left;}// 如果当前节点的Key小于目标Key// 当前节点应该向右子树走else if (cur->_key < key){parent = cur;cur = cur->_right;}else{// 找到了相同的 key, 在这里不插入return false;}}// cur 走到了空, 即 cur 就是合适的位置cur = new Node(key);// 我们需要判断cur是parent的左节点还是右节点// 如果key小于parent的key,那么插入左节点if (key < parent->_key)parent->_left = cur;// 反之连接到右节点elseparent->_right = cur;return true;}}bool find(const T& key){// 1. 从根节点开始Node* cur = _root;while (cur){// 2. 如果当前关键字大于目标关键字,那么向左子树走if (cur->_key > key)cur = cur->_left;// 3. 如果小于目标关键字,那么向右子树走else if (cur->_key < key)cur = cur->_right;// 4. 相等,就返回trueelsereturn true;}// 5. 循环结束,说明没找到, 返回falsereturn false;}bool erase(const T& key){// 先找要删除的节点Node* del = _root;Node* del_parent = nullptr;while (del){if (del->_key < key){del_parent = del;del = del->_right;}else if (del->_key > key){del_parent = del;del = del->_left;}else{// 锁定了要删除的节点// 分三种情况:// case 1: 左子树为空if (del->_left == nullptr){// 如果要删除的节点是根if (del == _root){Node* newroot = del->_right;delete _root;_root = newroot;}else{// 托孤法删除if (del_parent->_left == del)del_parent->_left = del->_right;elsedel_parent->_right = del->_right;delete del;del = nullptr;}}// case 2: 右子树为空else if (del->_right == nullptr){if (_root == del){Node* newroot = del->_left;delete _root;_root = newroot;}else{if (del_parent->_left == del)del_parent->_left = del->_left;elsedel_parent->_right = del->_left;delete del;del = nullptr;}}// case 3: 左右子树都不为空else{// 从被删除节点开始, 找右子树的最小(左)节点 || 找左子树的最大(右)节点if (del->_right)_erase_right_min_node(del);else_erase_left_max_node(del);}return true;}}return false;}bool find_recursion(const T& key){return _find_recursion(_root, key);}bool insert_recursion(const T& key){return _insert_recursion(_root, key);}bool erase_recursion(const T& key){return _erase_recursion(_root, key);}~BinarySearchTree(){_BSTDestroy(_root);}BinarySearchTree(const BinarySearchTree<T>& copy){_root = _creat_new_root(copy._root);}// 传值传参会进行拷贝构造BinarySearchTree<T>& operator=(BinarySearchTree<T> copy){std::swap(_root, copy._root);return *this;}void InOrder(){_InOrder(_root);std::cout << std::endl;}private:void _InOrder(Node* root){if (root){_InOrder(root->_left);std::cout << root->_key << " ";_InOrder(root->_right);}}bool _find_recursion(Node* root, const T& key){if (root == nullptr)return false;else{if (root->_key < key)return _find_recursion(root->_right, key);else if (root->_key > key)_find_recursion(root->_left, key);elsereturn true;}}bool _insert_recursion(Node*& root, const T& key){if (root == nullptr){root = new Node(key);return true;}else{if (root->_key < key)return _insert_recursion(root->_right, key);else if (root->_key > key)return _insert_recursion(root->_left, key);elsereturn false;}}void _erase_right_min_node(Node* del){// 从被删除结点开始, 找右子树的最小(左)节点Node* right_min = del->_right;// 并记录这个节点的父亲节点, 让其从del开始Node* right_min_parent = del;while (right_min->_left){right_min_parent = right_min;right_min = right_min->_left;}// 交换这个节点和要删除节点的 keystd::swap(del->_key, right_min->_key);// 将删除 del 转化为删除 right_min (托孤法删除)if (right_min_parent->_left == right_min)right_min_parent->_left = right_min->_right;elseright_min_parent->_right = right_min->_right;delete right_min;right_min = nullptr;}void _erase_left_max_node(Node* del){// 从被删除节点开始, 找左子树的最大(右)节点Node* left_max = del->_left;// 并记录这个节点的父亲节点, 让其从del开始Node* left_max_parent = del;while (left_max->_right){left_max_parent = left_max;left_max = left_max->_right;}// 交换这个节点和要删除节点的 keystd::swap(del->_key, left_max->_key);// 将删除 del 转化为删除 left_max (托孤法删除)if (left_max_parent->_left == left_max)left_max_parent->_left = left_max->_left;elseleft_max_parent->_right = left_max->_left;delete left_max;left_max = nullptr;}bool _erase_recursion(Node*& root, const T& key){if (!root)return false;else{// 如果当前节点的key > 目标key,那么递归它的左子树即可if (root->_key > key)return _erase_recursion(root->_left, key);// 如果当前节点的key < 目标key,那么递归它的右子树即可else if (root->_key < key)return _erase_recursion(root->_right, key);// 如果找到了,进行删除else{// 此时的root就是要删除的节点Node* del = root;// a. 左子树为空if (root->_left == nullptr)root = root->_right;// b. 右子树为空else if (root->_right == nullptr)root = root->_left;// c. 左右子树都不为空else{// 左子树的最右节点Node* left_max = root->_left;while (left_max->_right)left_max = left_max->_right;// 交换"合适节点"和"被删除节点"的keystd::swap(left_max->_key, root->_key);// 在这里递归左子树即可return _erase_recursion(root->_left, key);}delete del;del = nullptr;return true;}}}Node* _creat_new_root(Node* root){// 如果遇到空了,就不用构造了if (root == nullptr)return nullptr;else{// 根据前序的思想(NLR),依次构造它的根、左子树、右子树 // 同时将它们连接起来Node* new_root = new Node(root->_key);new_root->_left = _creat_new_root(root->_left);new_root->_right = _creat_new_root(root->_right);return new_root;}}// 注意我们这里传递的是根的引用void _BSTDestroy(Node*& root){if (root == nullptr)return;else{// 依据后序的思想_BSTDestroy(root->_left);_BSTDestroy(root->_right);delete root;root = nullptr;}}private:Node* _root;};
}#endif二叉树进阶 --- 中,结束。
相关文章:

二叉树进阶 --- 中
目录 1. find 的递归实现 2. insert 的递归实现 3. erase 的递归实现 3.1. 被删除的节点右孩子为空 3.2. 被删除的节点左孩子为空 3.3. 被删除的节点左右孩子都不为空 4. 析构函数的实现 5. copy constructor的实现 6. 赋值运算符重载 7. 搜索二叉树的完整实现 1. fi…...

ChatGPT DALL-E绘图,制作各种表情包,实现穿衣风格的自由切换
DALL-E绘图功能探索: 1、保持人物形象一致,适配更多的表情、动作 2、改变穿衣风格 3、小女孩的不同年龄段展示 4、不同社交平台的个性头像创作 如果不会写代码,可以问GPT。使用地址:我的GPT4 视频,B站会发&#…...

程序环境和预处理、编译链接过程、编译的几个阶段、运行环境、预定义符号等的介绍
文章目录 前言一、程序的翻译环境和执行环境二、编译链接过程三、编译的几个阶段四、运行环境五、预定义符号总结 前言 程序环境和预处理、编译链接过程、编译的几个阶段、运行环境、预定义符号的介绍。 一、程序的翻译环境和执行环境 在 ANSI C 的任何一种实现中,…...

MySQL导入导出详细教程
导出 语法 mysqldump [OPTIONS] database [tables] mysqldump [OPTIONS] --databases [OPTIONS] DB1 [DB2 DB3...] mysqldump [OPTIONS] --all-databases [OPTIONS]导出所有数据库 mysqldump -uroot -proot --all-databases >/tmp/all.sql导出db1、db2两个数据库的所有数…...

STM32F103学习笔记 | 8. 二,八,十,十六进制表示方式
文章目录 进制基本信息参考文献 进制基本信息 C语言中的表示,前缀加0表示八进制数,前缀加0x表示十六进制数 基数数码名称描述代码和书本中的表示举例20 和 1二进制逢二进一,几乎所有的电子计算机内部都使用二进位制,分别为“0”…...

ROS2 工作空间
文章目录 ROS2 工作空间创建工作空间自动安装依赖编译工作空间设置环境变量参考链接 ROS2 工作空间 工作空间可以简单理解为工程目录。 ROS 系统中一个典型的工作空间结构如图所示: dev_ws: 根目录,里面会有四个子目录(子空间&a…...
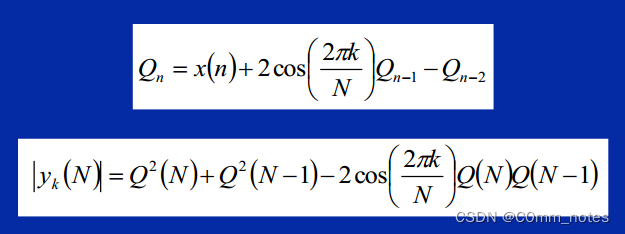
基于CCS5.5的双音多频(DTMF)信号检测仿真实验(①检测型音频文件②输入生成音频并检测)
DTMF的优点 我们知道,DTMF根本上仍然是频谱分析,基础还是DFT,但DFT通常需要对一整段数据做变换,而DTMF不同,每输入一个采样点就计算一次,更有利于硬件实现。 基于CCS的双音多频(DTMF)信号检测原理 公式详细推导 详细的公式推导在下面这篇博客中已经进行了详细的描述,…...
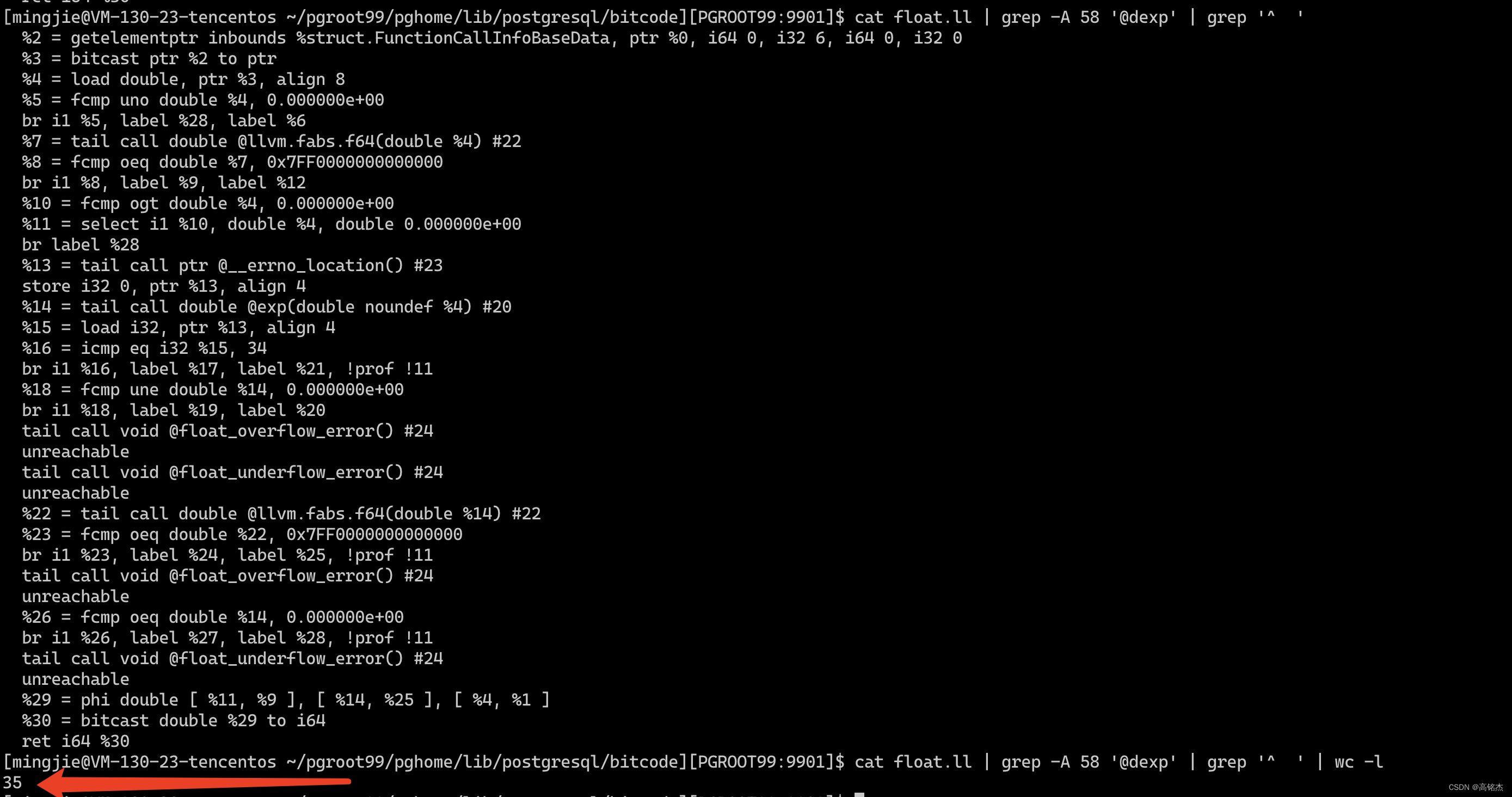
Postgresql中JIT函数能否inline的依据function_inlinable
相关 《Postgresql源码(128)深入分析JIT中的函数内联llvm_inline》 《LLVM的ThinLTO编译优化技术在Postgresql中的应用》 前置阅读:《Postgresql源码(128)深入分析JIT中的函数内联llvm_inline》 在JIT inline函数的过…...

存储过程作为初始化数据例子
查询出每个人员,为每个人员插入11条数据,作为初始化数据 oracle存储过程 CREATE OR REPLACE PROCEDURE initialize_order_warn_config ISv_id NUMBER; BEGINSELECT COALESCE(MAX(id), 0) INTO v_id FROM order_warn_config;FOR rec IN (SELECT DISTINCT…...

【数据分析】 JupyterNotebook安装及使用简介
各位大佬好 ,这里是阿川的博客 , 祝您变得更强 个人主页:在线OJ的阿川 大佬的支持和鼓励,将是我成长路上最大的动力 阿川水平有限,如有错误,欢迎大佬指正 在数据分析中,一般用Pycharm编辑代…...

nginx命令大全
以下是Nginx的一些常用命令,适用于Linux环境,部分命令在Windows系统下也适用,但命令形式可能有所不同: 查看Nginx版本号: nginx -v:简短显示版本号。nginx -V:详细显示版本号及编译配置信息。 启动Nginx…...

【数据结构】顺序表与链表的差异
顺序表和链表都是线性表,它们有着相似的部分,但是同时也有着很大的差异。 存储空间上的差异: 对于插入上的不同点,顺序表在空间不够时需要扩容,而如果在使用realloc函数去扩容,会有原地扩容和异地扩容两种情…...
小程序如何进行评分评价
小程序以其便捷、快速、无需安装的特点,成为了众多企业、品牌与消费者之间的重要连接桥梁。而评价评分机制,作为小程序中不可或缺的一环,对于提升用户体验、建立用户信任、促进商家与用户的互动等方面,都具有至关重要的意义。本文…...

【MATLAB源码-第206期】基于matlab的差分进化算法(DE)机器人栅格路径规划,输出做短路径图和适应度曲线。
操作环境: MATLAB 2022a 1、算法描述 差分进化算法(Differential Evolution, DE)是一种有效的实数编码的进化算法,主要用于解决实值函数的全局优化问题。本文将详细介绍差分进化算法的背景、原理、操作步骤、参数选择以及实际应…...
Tkinter笔记(三):控件的定位(1))
Python图形界面(GUI)Tkinter笔记(三):控件的定位(1)
Tkinter(GUI)设计图形界面时有三种控件的包装方法去定位各控件在窗口(父容器、根窗口)上的位置。 【1】pack()方法:用方位来定位位置,类似于Word文档中的文字对齐方式。 【2】grid()方法:用二维表格式的坐标值定位,类似于EXCEL单位元。 【3】place()方法:用窗口的像…...
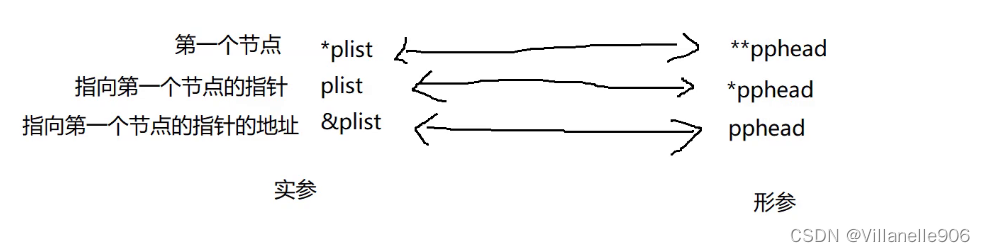
数据结构--单链表 详解(附代码
目录: 1:链表的概念及结构 2:实现单链表 3:常见疑问 解答 (看到最后!!) 一:链表的概念及结构 1.1 概念: 链表是⼀种 物理存储结构上非连续、非顺序的 存储结…...

leetcode 1749.任意子数组和的绝对值的最大值
思路:dp 说到绝对值,大家肯定不陌生,但是用在dp上就会使问题变得稍微复杂一些了。 我们在最大子数组和的那道题中知道,在状态转移的时候,我们会舍弃掉为负数的连续部分,重新构建连续的子串。但是…...

Linux进程——进程地址空间
前言:在讲完环境变量后,相信大家对Linux有更进一步的认识,而Linux进程概念到这也快接近尾声了,现在我们了解Linux进程中的地址空间! 本篇主要内容: 了解程序地址空间 理解进程地址空间 探究页表和虚拟地址空…...

基于 LlaMA 3 + LangGraph 在windows本地部署大模型 (三)
基于 LlaMA 3 LangGraph 在windows本地部署大模型 (三) 大家继续看 https://lilianweng.github.io/posts/2023-06-23-agent/的文档内容 第二部分:内存 记忆的类型 记忆可以定义为用于获取、存储、保留以及随后检索信息的过程。人脑中有多…...
python3如何安装bs4
在python官网找到beautifulsoup模块的下载页面,点击"downloap"将该模块的安装包下载到本地。 将该安装包解压,然后在打开cmd,并通过cmd进入到该安装包解压后的文件夹目录下。 在该文件目录下输入"python install setup.py&quo…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...
