国产操作系统下Chrome的命令行使用 _ 统信 _ 麒麟
原文链接:国产操作系统下Chrome的命令行使用 | 统信 | 麒麟
Hello,大家好啊!今天我们来聊聊如何在国产操作系统上使用命令行操作Google Chrome。无论是进行自动化测试、网页截图还是网页数据抓取,使用命令行操作Google Chrome都能大大提高效率。本文将详细介绍在统信UOS、麒麟KOS等国产操作系统上,如何通过命令行启动和控制Google Chrome。
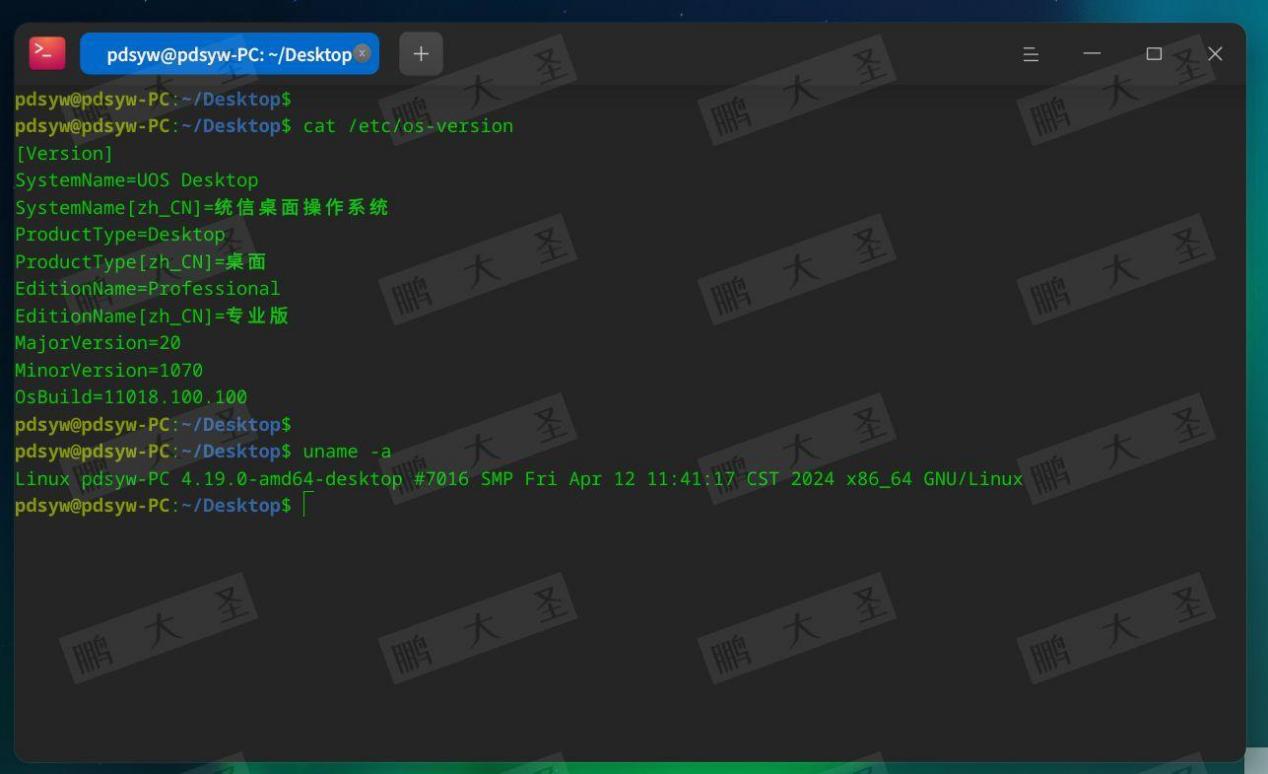
1.查看系统信息
pdsyw@pdsyw-PC:~/Desktop$ cat /etc/os-version
pdsyw@pdsyw-PC:~/Desktop$ uname -a
2.安装Chrome
3.打开Chrome浏览器
pdsyw@pdsyw-PC:~/Desktop$ /opt/apps/cn.google.chrome-pre/files/google/chrome/google-chrome
4.打开特定URL
pdsyw@pdsyw-PC:~/Desktop$ /opt/apps/cn.google.chrome-pre/files/google/chrome/google-chrome https://www.chinauos.com
5.新窗口打开
pdsyw@pdsyw-PC:~/Desktop$ /opt/apps/cn.google.chrome-pre/files/google/chrome/google-chrome --new-window

6.隐身模式
pdsyw@pdsyw-PC:~/Desktop$ /opt/apps/cn.google.chrome-pre/files/google/chrome/google-chrome --incognito

7.指定用户数据目录
pdsyw@pdsyw-PC:~/Desktop$ /opt/apps/cn.google.chrome-pre/files/google/chrome/google-chrome --user-data-dir="/home/pdsyw/chrome"
8.禁用扩展
pdsyw@pdsyw-PC:~/Desktop$ /opt/apps/cn.google.chrome-pre/files/google/chrome/google-chrome --disable-extensions
9.禁用沙盒
pdsyw@pdsyw-PC:~/Desktop$ /opt/apps/cn.google.chrome-pre/files/google/chrome/google-chrome --no-sandbox

10.全屏模式启动
pdsyw@pdsyw-PC:~/Desktop$ /opt/apps/cn.google.chrome-pre/files/google/chrome/google-chrome --start-fullscreen

11.应用模式
(无地址栏和工具栏的窗口)
pdsyw@pdsyw-PC:~/Desktop$ /opt/apps/cn.google.chrome-pre/files/google/chrome/google-chrome --app=http://www.chinauos.com
通过以上命令,您可以在国产操作系统上高效地使用Google Chrome进行各种操作,这对于需要自动化和脚本控制的任务尤为便利。希望这篇文章对大家有所帮助,如果您觉得有用,请分享和转发。同时,别忘了点个关注和在看,以便未来获取更多实用的技术信息和解决方案。感谢大家的阅读,我们下次再见!
相关文章:

国产操作系统下Chrome的命令行使用 _ 统信 _ 麒麟
原文链接:国产操作系统下Chrome的命令行使用 | 统信 | 麒麟 Hello,大家好啊!今天我们来聊聊如何在国产操作系统上使用命令行操作Google Chrome。无论是进行自动化测试、网页截图还是网页数据抓取,使用命令行操作Google Chrome都能…...
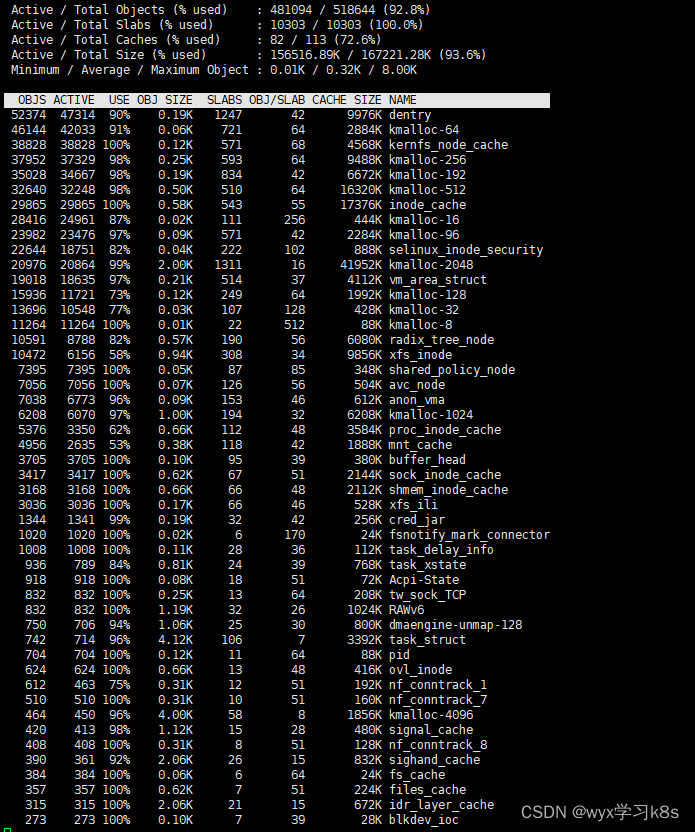
linux性能监控之slabtop
slabtop命令是以实时的方式显示内核slab缓冲区的细节信息,是linux自带的命令 [rootk8s-master ~]# slabtop --helpUsage:slabtop [options]Options:-d, --delay <secs> delay updates-o, --once only display once, then exit-s, --sort <char&…...

Allure 在 Python 中的安装与使用
Allure 是一个灵活轻量级的测试报告工具,它能够生成详细且富有洞察力的测试报告。在 Python 中,Allure 通常与 Pytest 结合使用,以提供更加丰富的测试结果展示。下面我将介绍关于如何在 Python 中使用 Allure 的详细操作。 一、环境准备 在…...

python实现动态时钟功能
欢迎关注我👆,收藏下次不迷路┗|`O′|┛ 嗷~~ 一.前言 时钟,也被称为钟表,是一种用于测量、记录时间的仪器。时钟通常由时针、分针、秒针等计时仪器组成,是现代社会不可或缺的一种计时工具。它的发明和使用极大地改变了人类的生活方式和时间观念。 时钟的类型有很多,…...
QueryPerformanceCounter实现高精度uS(微妙)延时
参考连接 C# 利用Kernel32的QueryPerformanceCounter封装的 高精度定时器Timer_kernel32.dll queryperformancecounter-CSDN博客https://blog.csdn.net/wuyuander/article/details/111831973 特此记录 anlog 2024年5月11日...

Logstash详解
Logstash详解:构建强大日志收集与处理管道的利器 一、引言 在大数据和云计算的时代,日志数据作为企业运营和故障排查的重要依据,其收集、处理和分析能力显得尤为重要。Logstash,作为一款强大的日志收集、处理和转发工具…...

QT设计模式:适配器模式
基本概念 适配器模式(Adapter Pattern)是一种结构型设计模式,允许将一个类的接口转换成客户端所期望的另一个接口,可以让原本由于接口不兼容而不能一起工作的类能够一起工作。 适配器模式需要实现的部分为: Target类…...
开发规范相关
1.对IDEA集成的代码检查 或 AliBaBa的代码检查 定义的规则进行取消或新增 代码自动扫描检查对于代码规范来说至关重要,但有时,我们希望忽略掉某些不必要的检查,比如忽略掉这个检查 可以如下操作 此时即可不再提示告警...
——Set操作)
C++ 容器(五)——Set操作
一、Set容器定义 set 是一个有序关联容器,其中的元素按照升序排列,且不允许重复元素。 set 中的元素是唯一的,即任意两个元素不能相等。 1、set 可以用来对元素进行排序,因为它会自动对元素进行有序排列。 2、set 可以用来去重,当我们需要对一个容器中的元素进行去重操…...

【数字IC设计】芯片设计中的RDC
RDC问题定义 在芯片设计中,RDC是reset domain crossing 的缩写,类似于CDC(clock domain crossing),由于现在SOC芯片是有很多ECUs组成,为了使整个系统能够快速从复位中恢复, 用户希望SOC里面每个ECU模块都可以有自己独立的异步复位信号,这样可以在出问题的时候只复位有错…...

spark history server异常
现象:spark 日志文件突然新增了很多.hprof文件, 查找日志spark配置参数spark_log_dir进入日志目录: 查看historyServer日志: Spark Command: /usr/lib/jvm/java-1.8.0/bin/java -cp /opt/apps/JINDOSDK/jindosdk-current/lib/*:/…...
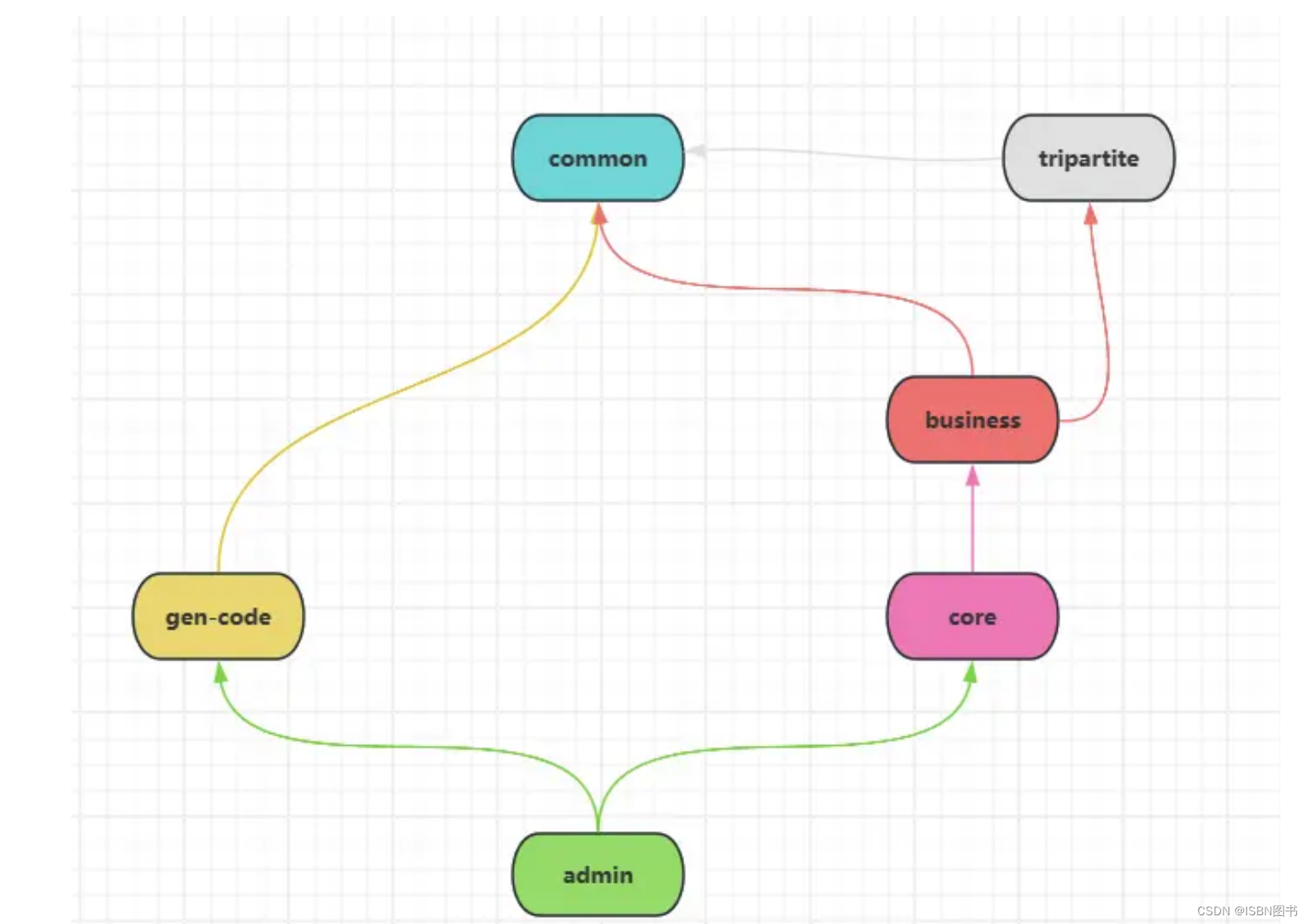
一个优秀 Maven 项目,各 Model 间最佳继承设计方案
1.单一职责原则 (Single Responsibility Principle): 每个模块应该专注于执行一个清晰且明确定义的功能,遵循单一职责原则,以降低模块的复杂性。 2.高内聚性 (High Cohesion): 模块内的组件和类应该紧密相关,共同实现模块的目标。高内聚性…...

MATLAB概述
文章目录 目录结构搜索路径高频命令clearclf/closeclc/homewho/whosformatsave/loadcd/pwdhelp/docsprintf/fprintf/disp tips MATLAB [1] 是美国 MathWorks公司出品的商业 数学软件,用于算法开发、数据可视化、数据分析以及 数值计算的高级技术计算语言和交互式…...

Redis5.0的Stream数据结构
Redis 5.0中引入的Stream数据结构是一种新的、持久化的、可查询的、可扩展的消息队列服务。它可以被视为一个日志或消息队列,由一个有序的、不断增长的日志序列来存储事件流数据。以下是关于Redis 5.0 Stream数据结构的详细解释: 一、Stream数据结构概述…...

避坑指南!RK3588香橙派yolov5生成RKNN模型!
地址1,转换模型 地址2,转换模型 地址3,解决ppa 下载k2 本文目录 一、将.pt模型转为onnx模型文件。(Windows)二、将.onnx模型转为.rknn模型文件。(Linux)三、将.rknn模型部署到开发板RK3588中…...
)
算法学习笔记(Nim游戏)
N i m Nim Nim游戏 n n n堆物品,每堆有 a i a_i ai个,每个玩家轮流取走任意一堆的任意个物品,但不能不取,取走最后一个物品的人获胜。 N i m Nim Nim游戏是一种经典的公平组合游戏。现在对它进行分析。 首先定义两个博弈中的状…...
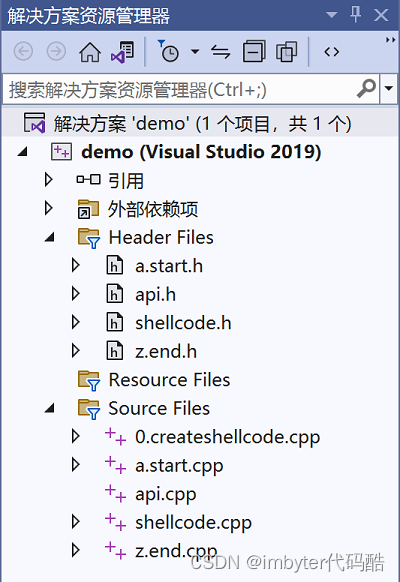
第13节 第二种shellcode编写实战(2)
在第二种shellcode编写实战(1)的基础上,新增加一个CAPI类,将所有用到的函数都在这个类中做动态调用的处理,这样使得整个shellcode功能结构更加清晰。 1. 新建类CAPI(即api.h和api.cpp两个文件): api.h&…...
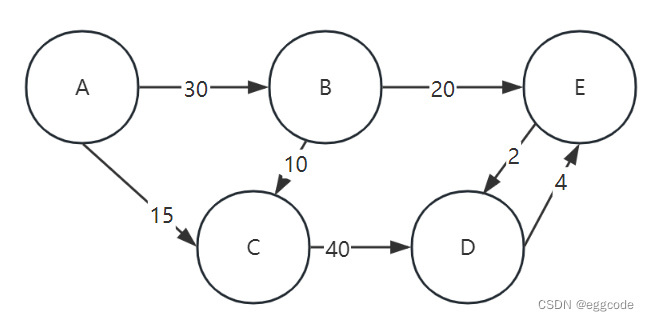
【QuikGraph】C#调用第三方库实现迪杰斯特拉(Dijkstra)算法功能
QuikGraph库介绍 项目地址:https://github.com/KeRNeLith/QuikGraph QuikGraph为.NET提供了通用的有向/无向图数据结构和算法。 QuikGraph提供了深度优先搜索、广度优先搜索、A*搜索、最短路径、k最短路径,最大流量、最小生成树等算法。 QuikGraph最初…...

查看ubuntu当前路径的剩余存储空间
要查看Ubuntu当前路径所在磁盘分区的剩余存储空间,应该使用df命令,而不是du命令,因为df命令能显示磁盘分区的使用情况,包括总容量、已用空间和可用空间。为了使输出更易于阅读,可以加上-h选项。如果你还想知道特定挂载…...

利用预训练模型和迁移学习打造智能狗门
引言 在深度学习的世界里,预训练模型和迁移学习是两个强大的概念,它们允许我们利用已有的模型和知识来解决新的问题。在本博客中,我们将探索如何使用预训练的模型来创建一个智能狗门,这个系统将能够识别狗并允许它们进入…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...

Selenium常用函数介绍
目录 一,元素定位 1.1 cssSeector 1.2 xpath 二,操作测试对象 三,窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四,弹窗 五,等待 六,导航 七,文件上传 …...

STM32HAL库USART源代码解析及应用
STM32HAL库USART源代码解析 前言STM32CubeIDE配置串口USART和UART的选择使用模式参数设置GPIO配置DMA配置中断配置硬件流控制使能生成代码解析和使用方法串口初始化__UART_HandleTypeDef结构体浅析HAL库代码实际使用方法使用轮询方式发送使用轮询方式接收使用中断方式发送使用中…...
