网络安全科普:保护你的数字生活
# 网络安全科普:保护你的数字生活
## 引言
在数字化时代,网络安全已成为每个人都必须面对的问题。从个人隐私保护到金融交易安全,网络的安全性直接关系到我们的日常生活。因此,普及网络安全知识,提高公众的网络安全意识显得尤为重要。
## 网络安全的重要性
网络安全的核心在于保护网络空间不受威胁、破坏、干扰,保护个人信息不被非法获取和使用。根据,网络安全不仅关乎国家安全,也是经济社会稳定运行的基石,与每个网民的切身利益息息相关。
## 常见的网络安全风险
1. **电信网络诈骗**:通过电话、短信、网络等方式进行的诈骗行为,如中提到的刷单返利、虚假投资理财等。
2. **个人信息泄露**:个人资料在网上被非法获取,可能用于诈骗或其他犯罪活动。
3. **恶意软件**:包括病毒、木马、勒索软件等,它们可以破坏系统、窃取信息或锁住用户文件。
## 个人如何提升网络安全防护
1. **警惕诈骗信息**:对于要求提供个人信息的可疑电话、短信或电子邮件保持警惕。
2. **使用复杂密码**:为不同的账户设置独特且复杂的密码,并定期更换。
3. **定期更新软件**:保持操作系统和应用程序更新到最新版本,以利用最新的安全补丁。
4. **避免不安全的网络连接**:不连接不明Wi-Fi,尤其是在公共场合。
5. **备份重要数据**:定期备份重要文件,以防数据丢失或加密勒索。
## 国家层面的网络安全措施
1. **法律法规**:如《中华人民共和国网络安全法》和《中华人民共和国数据安全法》,为网络安全提供法律基础。
2. **安全教育**:通过国家网络安全宣传周等活动,提升全民网络安全意识。
3. **人才培养**:建立网络安全学科,培养专业人才,如中提到的一流网络安全学院建设。
## 结语
网络安全需要我们每个人的共同努力。通过提升个人网络安全意识、学习网络安全知识、遵守网络安全法律法规,我们可以更好地保护自己的网络空间安全,共筑网络安全防线。
相关文章:

网络安全科普:保护你的数字生活
# 网络安全科普:保护你的数字生活 ## 引言 在数字化时代,网络安全已成为每个人都必须面对的问题。从个人隐私保护到金融交易安全,网络的安全性直接关系到我们的日常生活。因此,普及网络安全知识,提高公众的网络安全意…...

Java实战:递归查找指定后缀名的文件
在日常的软件开发中,经常需要处理文件操作。假设我们有一个需求:从一个包含大量JSON文件的文件夹中提取出所有的JSON文件以进行进一步处理。本文将介绍如何利用Java编写一个高效的方法来递归查找指定后缀名的文件。 代码实现: import java.i…...
Linux 操作系统网络编程1
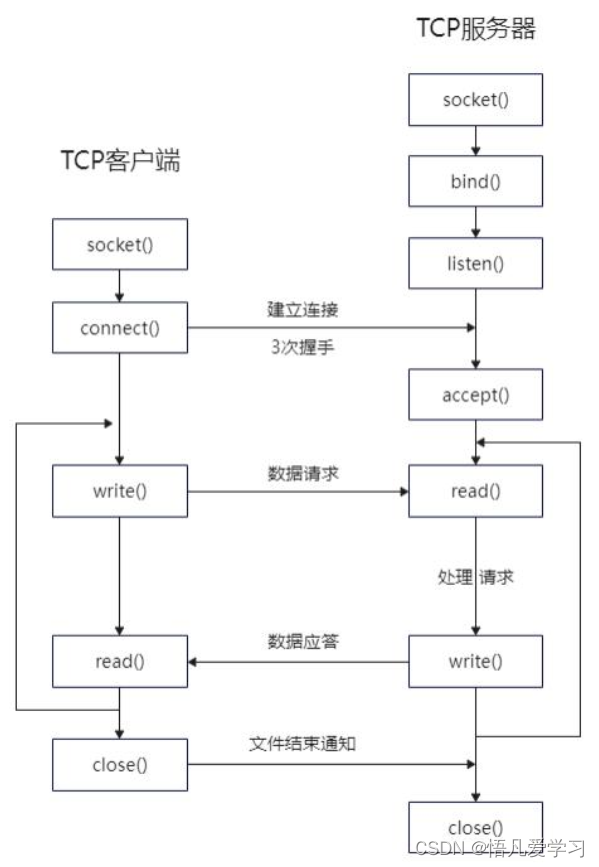
目录 1、网络编程 1.1 OSI 网络七层模型 1.1.1 OSI 参考模型 1.1.2 网络数据传输过程 2 传输层通信协议 2.1 TCP 2.1.1 TCP的3次握手过程 2.1.2 TCP四次挥手过程 2.2 UDP 3 网络编程的IP地址 4 端口 5 套接字 1、网络编程 1.1 OSI 网络七层模型 1.1.1 OSI 参考模型…...
成员、shared_future)
future wait_for()成员、shared_future
future wait_for()成员 wait_for():等待其异步操作操作完成或者超出等待,用于检查异步操作的状态。wait_for()可以接受一个std::chrono::duration类型的参数,它表示等待的最大时间,会返回一个std::future_status枚举值࿰…...

C++ list介绍(迭代器失效)
一、常用接口 reverse逆置 sort排序(默认升序) 仿函数greater<int> merge合并,可以全部合并,也可以一部分合并 unique:去重(先排序,再去重) remove:删除e值&#…...

codeforces 1809C
很巧妙的构造 题目链接 题目大意 要求构造长度为 n n n的数组满足以下条件 任意 i i i, − 1000 < a [ i ] < 1000 -1000<a[i]<1000 −1000<a[i]<1000有 k k k个和为正数的子串其余子串和为负数 思路 我们发现与子数组内元素的和有关&…...
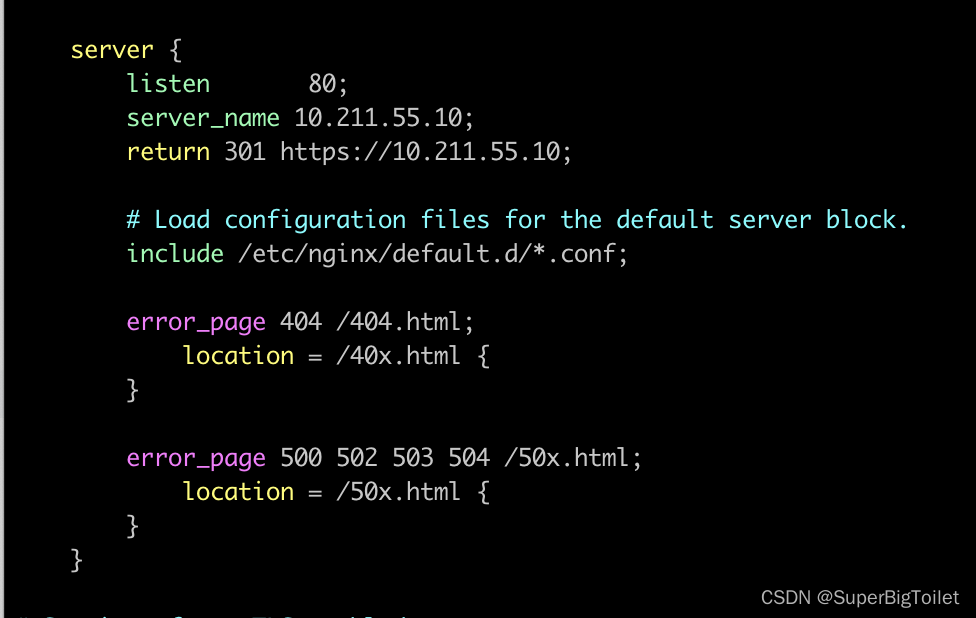
Nginx part3 创建一个https的网站
目录 HTTPS 公钥和密钥 加密解密方式: https搭建步骤 强调一下 1、准备环境 2、配置文件 3、制作证书 4、进行设置 HTTPS 啥是https,根据百度:HTTPS (全称:Hypertext Transfer Protocol Secure)&a…...

事件高级。
一、注册事件(绑定事件) 就是给元素添加事件 注册事件有两种方式:传统方式和方法监听注册方式 1 传统注册方式 方法监听注册事件 2、 addEventListener 事件监听方式 里面的事件类型是字符串,必定加引号,而且不带o…...

Vue从入门到实战Day04
一、组件的三大组成部分(结构/样式/逻辑) 1. scoped样式冲突 默认情况:写在组件中的样式会全局生效 -> 因此很容易造成多个组件之间的样式冲突问题。 1. 全局样式:默认组件中的样式会作用到全局 2. 局部样式:可以…...
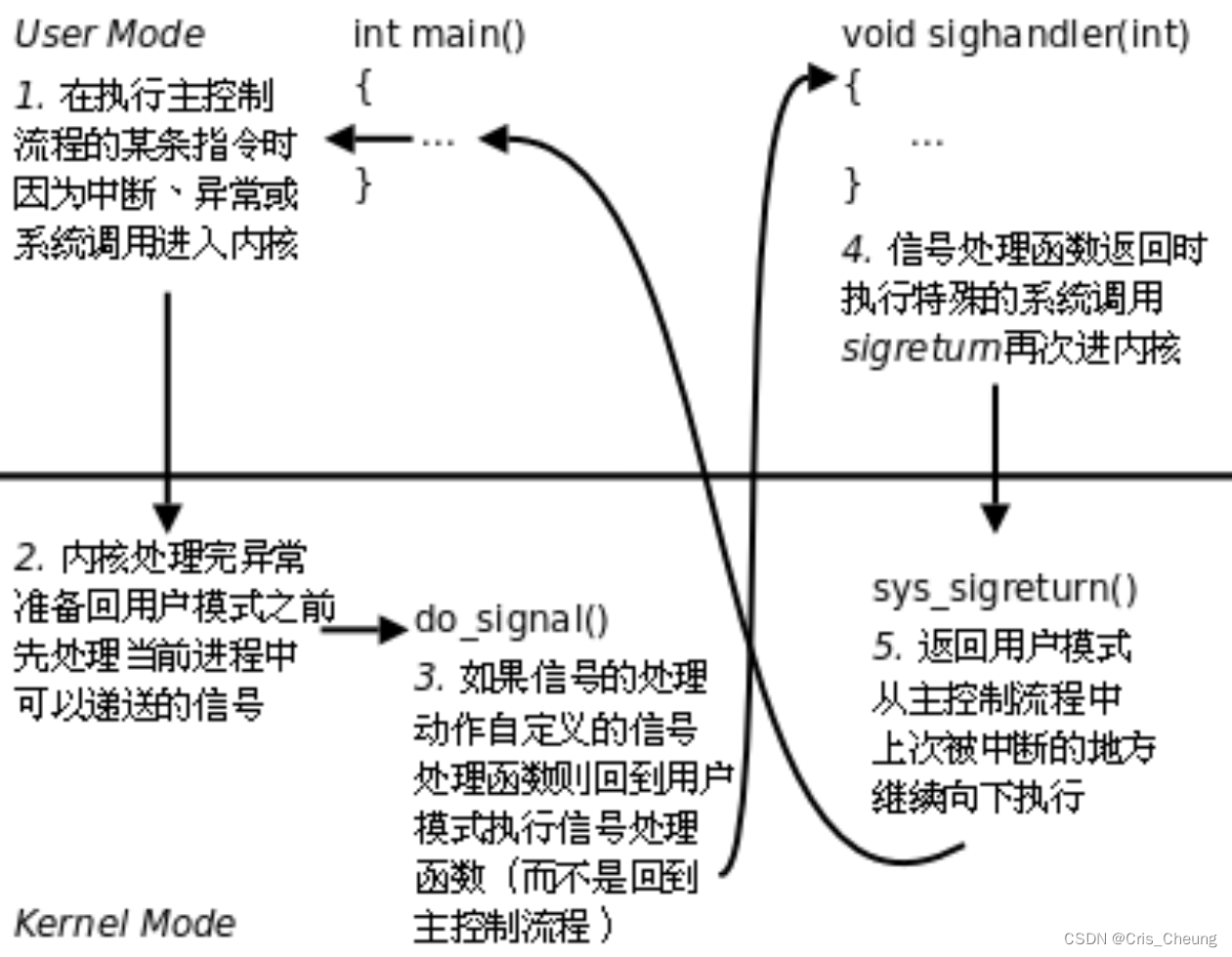
Linux学习笔记:信号
信号 在Linux中什么是信号信号的产生方式硬件产生的信号软件产生的信号异常产生的信号 进程对信号的处理信号的保存信号方法更改函数signal信号处理的更改恢复默认信号忽略 信号的管理信号集 sigset_t对信号集的操作 信号的捕捉过程 在Linux中什么是信号 在 Linux 系统中&…...

C#中的隐式类型转换和显式类型转换
在C#中,类型转换分为隐式类型转换(Implicit Type Conversion)和显式类型转换(Explicit Type Conversion),也称为隐式转换和强制转换。 隐式类型转换(Implicit Type Conversion) 隐…...

linux上如何排查JVM内存过高?
在Linux上排查JVM内存过高的问题,可以采用以下几种方法: 1. **使用top命令查看进程**:通过top命令可以观察到系统中资源占用情况,包括CPU和内存。当收到内存过高的报警时,可以使用top命令来查看是哪个进程的内存使用率…...
第四届上海理工大学程序设计全国挑战赛 J.上学 题解 DFS 容斥
上学 题目描述 usst 小学里有 n 名学生,他们分别居住在 n 个地点,第 i 名学生居住在第 i 个地点,这些地点由 n−1 条双向道路连接,保证任意两个地点之间可以通过若干条双向道路抵达。学校则位于另外的第 0 个地点,第…...

word-排版文本基本格式
1、文本的基本格式:字体格式、段落格式 2、段落:word排版的基本控制单位 3、每敲一次回车,为一个段落标记,注意区分换行符和段落标记,换行符为指向下的箭头,段落标记为带拐弯的箭头,换行符&…...
)
目标检测YOLO实战应用案例100讲-无监督领域自适应目标检测方法研究与应用(五)
目录 多源无监督领域自适应目标检测方法 4.1研究现状及问题形成 4.2相关工作详述...
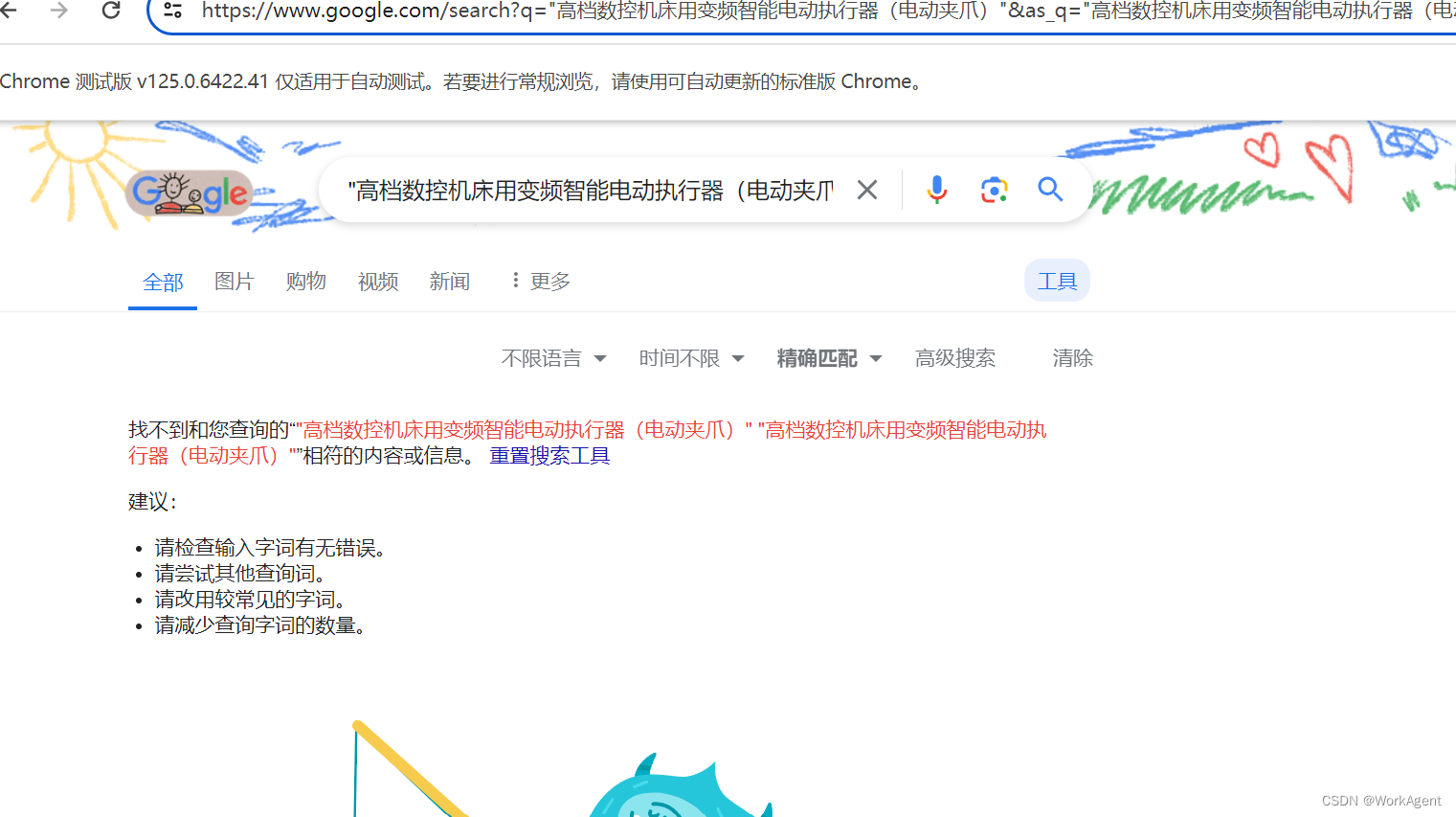
通过python实现Google的精准搜索
问题背景: 我想通过Google或者其他网站通过精准搜索确认该产品是否存在,但是即使该产品不存在Google也会返回一些相关的url链接,现在想通过python实现搜索结果的精准匹配以确认该产品是否为正确的名称【可以通过google搜索到,如果…...
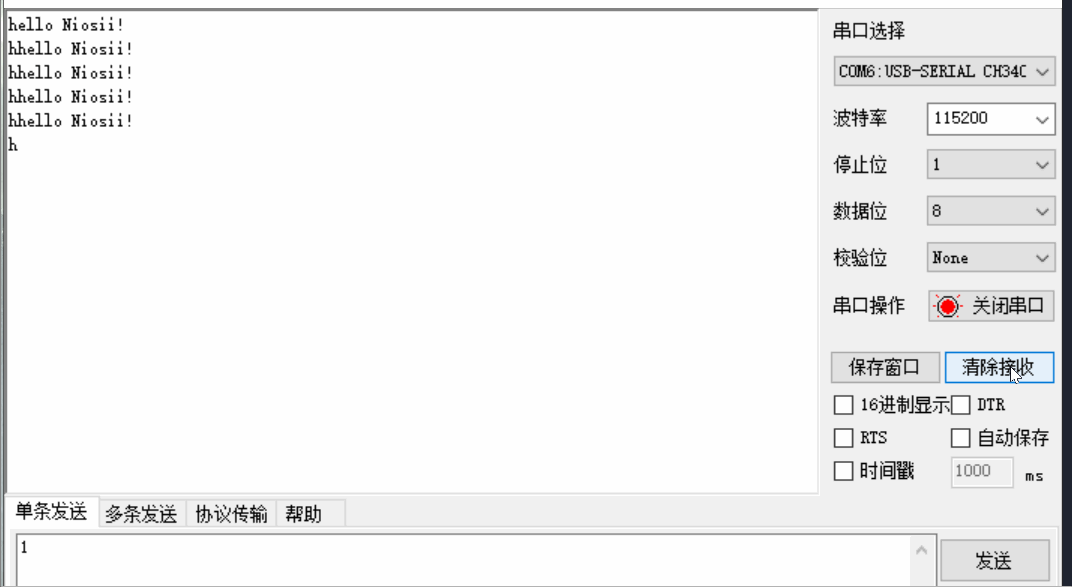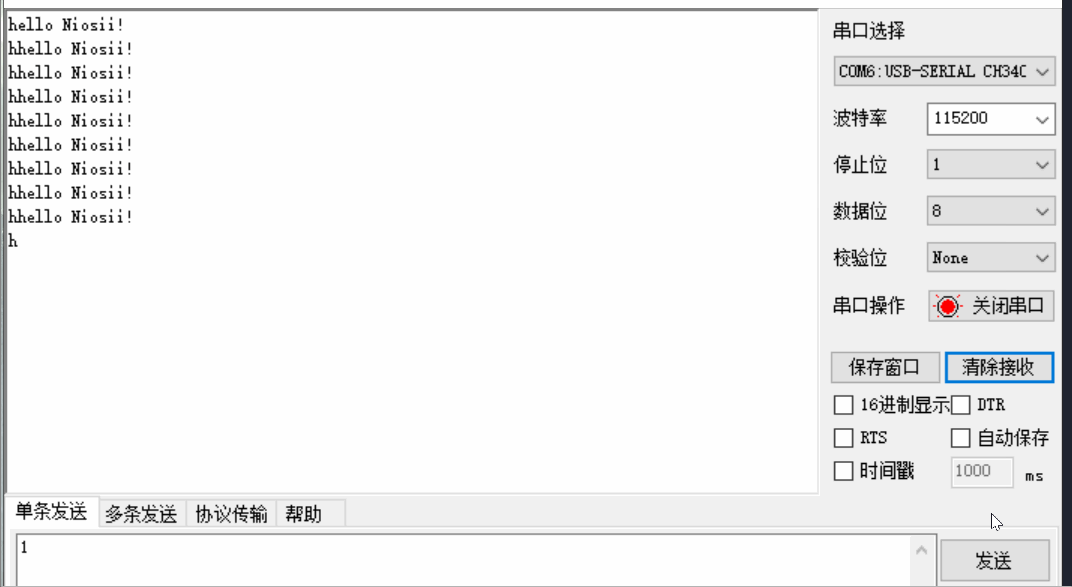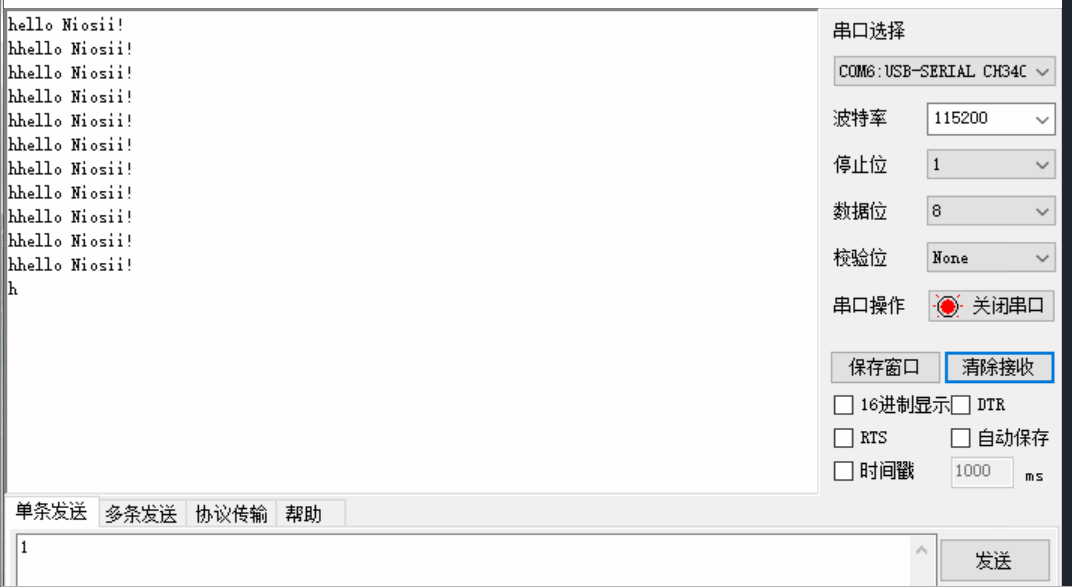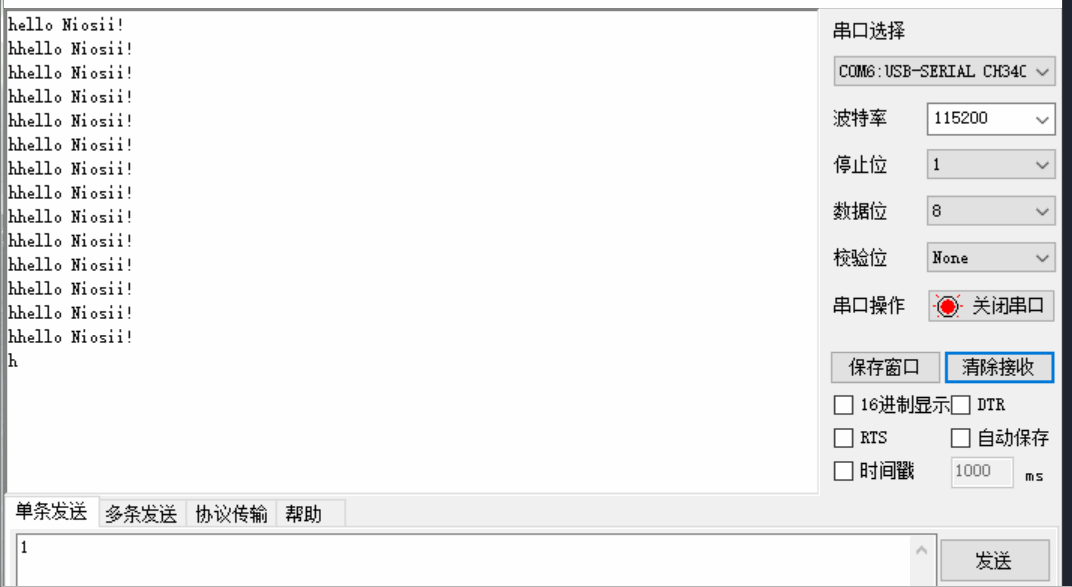
Nios-II编程入门实验
文章目录 一 Verilog实现流水灯二 Nios实现流水灯2.1 创建项目2.2 SOPC添加模块2.3 SOPC输入输出连接2.4 Generate2.5 软件部分2.6 运行结果 三 Verilog实现串口3.1 代码3.2 引脚3.3 效果 四 Nios2实现串口4.1 sopc硬件设计4.2 top文件4.3 软件代码4.4 实现效果 五 参考资料六 …...

从0开始学python(七)
目录 前言 1 break、continue和pass函数 1.1 break 1.2 continue 1.3 pass 2、序列的索引及切片操作 2.1字符串的索引和切片 2.1.1 字符串索引 2.1.2 字符串切片 总结 前言 上一篇文章我们介绍了python中的循环结构,包括for和while的使用。本章接着往下讲。…...

【二叉树算法题记录】404. 左叶子之和
题目描述 给定二叉树的根节点 root ,返回所有左叶子之和。 题目分析 其实这题无论是迭代法还是递归法,最重要的是要明确判断左叶子的条件:当前节点有左孩子,且这个左孩子没有它的左孩子和右孩子。 迭代法 感觉只要二叉树相关…...
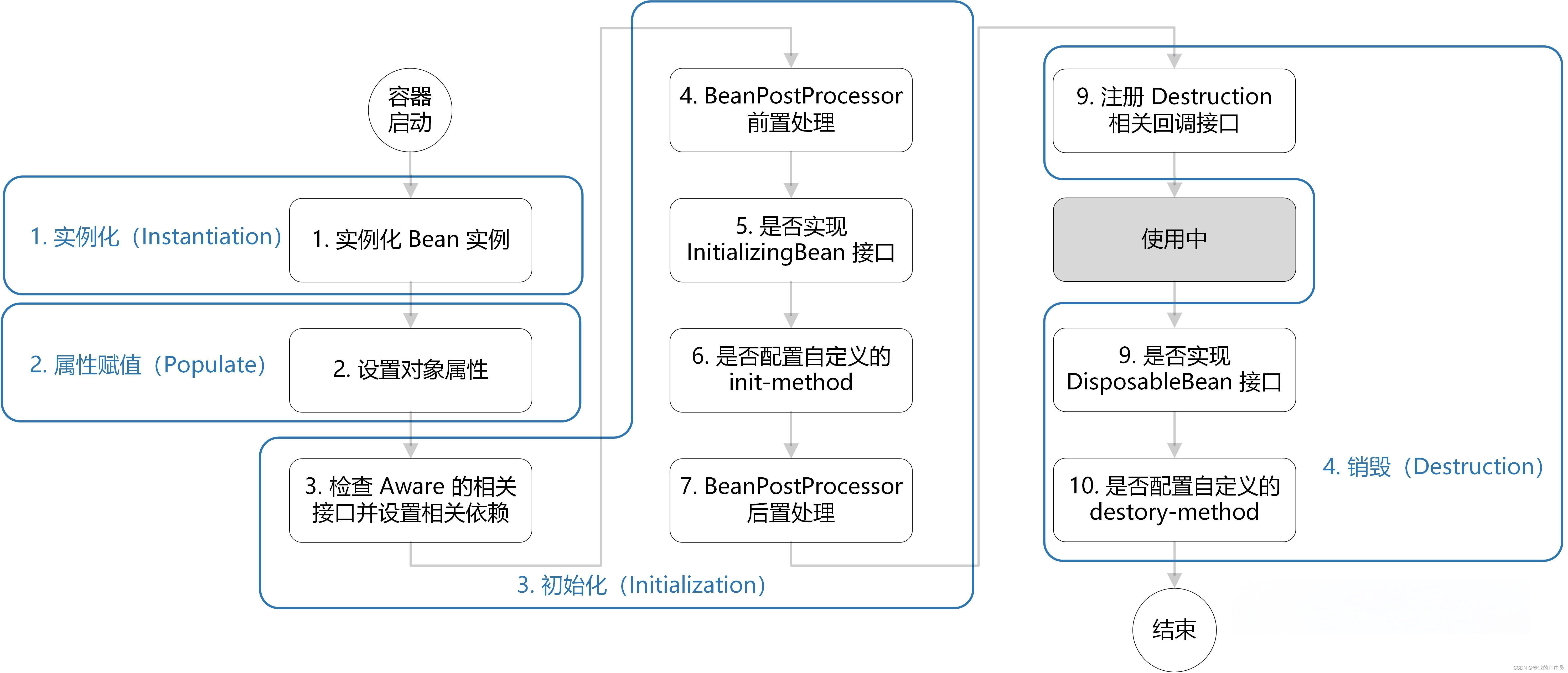
面试集中营—Spring篇
Spring 框架的好处 1、轻量:spring是轻量的,基本的版本大约2MB; 2、IOC:控制反转,Spring的IOC机制使得对象之间的依赖不再需要我们自己来控制了,而是由容易来控制,一个字:爽…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...

GraphQL 实战篇:Apollo Client 配置与缓存
GraphQL 实战篇:Apollo Client 配置与缓存 上一篇:GraphQL 入门篇:基础查询语法 依旧和上一篇的笔记一样,主实操,没啥过多的细节讲解,代码具体在: https://github.com/GoldenaArcher/graphql…...

第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10+pip3.10)
第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10pip3.10) 一:前言二:安装编译依赖二:安装Python3.10三:安装PIP3.10四:安装Paddlepaddle基础框架4.1…...
