代数结构:5、格与布尔代数
16.1 偏序与格
偏序集:设P是集合,P上的二元关系“≤”满足以下三个条件,则称“≤”是P上的偏序关系(或部分序关系)
(1)自反性:a≤a,∀a∈P;
(2)反对称性:∀a,b∈P,若a≤b且b≤a,则a=b;
(3)传递性:∀a,b,c∈P,若a≤b且b≤c,则a≤c;
定义1 格
设 ( L , ⪯ ) (L,\preceq) (L,⪯)为偏序集,如果任意的$a,b\in L 有最小上界与最大下界时,称 有最小上界与最大下界时,称 有最小上界与最大下界时,称L 为 ‘ 格 ‘ ,以 为`格`,以 为‘格‘,以a\lor b = lub(a,b) ( l e a s t u p p e r b o n d ) 表示 (least upper bond)表示 (leastupperbond)表示a,b 的最小上界, 的最小上界, 的最小上界,a\land b =glb(a,b) ( g r e a t e s t l o w e r b o n d ) 表示 (greatest lower bond)表示 (greatestlowerbond)表示a,b$的最大下界。
定义2 覆盖
( L , ⪯ ) (L,\preceq) (L,⪯)为格,如果 a ⪯ b , a ≠ b a\preceq b,a\neq b a⪯b,a=b(记为 a ≺ b a\prec b a≺b),且不存在 u ∈ L − { a , b } u\in L-\{a,b\} u∈L−{a,b},使 a ≺ u ≺ b a\prec u \prec b a≺u≺b,则称 a a a覆盖 b b b.
链:若 a ≺ b a\prec b a≺b,如果有 c 1 , ⋯ , c k ∈ L , k ≥ 1 c_1,\cdots,c_k \in L,k\ge 1 c1,⋯,ck∈L,k≥1 ,使 c i + 1 c_{i+1} ci+1覆盖 c i ( u i = 1 , 2 , ⋯ , k − 1 ) c_i(ui=1,2,\cdots,k-1) ci(ui=1,2,⋯,k−1),且
a = c 1 ≺ c 2 ≺ ⋯ ≺ c k = b a=c_1\prec c_2\prec\cdots\prec c_k = b a=c1≺c2≺⋯≺ck=b
则称 c 1 , ⋯ , c k c_1,\cdots,c_k c1,⋯,ck为连接 a , b a,b a,b的链,如果L中的任意两个元素总有连接它们的链,则称 L L L是离散的。
有限的离散全序集的哈斯图由一条链组成
定义3 完全格
( L ; ≺ ) (L;\prec) (L;≺)为偏序集,当$\forall A\subseteq L 有最大下界、最小上界时, 有最大下界、最小上界时, 有最大下界、最小上界时,L 显然是格,称为 ‘ 完全格 ‘ , 显然是格,称为`完全格`, 显然是格,称为‘完全格‘,L 自身的最小上界是整个格 自身的最小上界是整个格 自身的最小上界是整个格L 的最大元,记为 1 ; 的最大元,记为1; 的最大元,记为1;L 自身的最小下界为整个格 自身的最小下界为整个格 自身的最小下界为整个格L 的最小元记为 0. 子集 的最小元记为0.子集 的最小元记为0.子集A$可以是有限的,也可以是无限的。
定理1 格的关系运算
( L , ⪯ ) (L,\preceq) (L,⪯)为格,则对任意 a , b ∈ L a,b\in L a,b∈L有
- a ≺ a ∨ b , a ∧ b ≺ a a\prec a\lor b ,a\land b \prec a a≺a∨b,a∧b≺a
- a ⪯ b ⟺ a ∨ b = b a\preceq b \Longleftrightarrow a\lor b =b a⪯b⟺a∨b=b
- a ⪯ b ⟺ a ∧ b = a a\preceq b \Longleftrightarrow a\land b = a a⪯b⟺a∧b=a
画个哈斯图是显然的,或者注意到按照定义,我们有 a ∨ b = l u b ( a , b ) , a ∧ b = g l b ( a , b ) a\lor b=lub(a,b),a\land b = glb(a,b) a∨b=lub(a,b),a∧b=glb(a,b),且若 a ⪯ b a\preceq b a⪯b,则 l u b ( a , b ) = b lub(a,b)=b lub(a,b)=b就容易得到了
定理2 格的运算律
- 幂等律: a ∧ a = a , a ∨ a = a a\land a = a, a\lor a = a a∧a=a,a∨a=a
- 交换律: a ∨ b = b ∨ a , a ∧ b = b ∧ a a\lor b=b\lor a,a\land b=b\land a a∨b=b∨a,a∧b=b∧a
- 结合律: a ∨ ( b ∨ c ) = ( a ∨ b ) ∨ c , a ∧ ( b ∧ c ) = ( a ∧ b ) ∧ c a\lor(b\lor c)=(a\lor b )\lor c,a\land(b\land c)=(a\land b)\land c a∨(b∨c)=(a∨b)∨c,a∧(b∧c)=(a∧b)∧c
- 吸收律: a ∨ ( a ∧ b ) = a , a ∧ ( a ∨ b ) = a a\lor(a\land b)=a,a\land(a\lor b)= a a∨(a∧b)=a,a∧(a∨b)=a
P211
那么我们可以将 [ L ; ∧ , ∨ ] [L;\land,\lor] [L;∧,∨]视为代数系统
引理 1 代数系统L中的等价关系
在 [ L ; ∨ , ∧ ] [L;\lor,\land] [L;∨,∧]中二元关系 ∨ , ∧ \lor,\land ∨,∧满足上述4条运算律,则 ∀ a , b ∈ L , a ∧ b = a ⟺ a ∨ b = b \forall a,b\in L ,a\land b= a\Longleftrightarrow a\lor b=b ∀a,b∈L,a∧b=a⟺a∨b=b
KaTeX parse error: Undefined control sequence: \and at position 38: …row a\lor b =(a\̲a̲n̲d̲ ̲b )\lor b =b(最后一步是吸收律)
a ∨ b = b ⇒ a ∧ b = a ∧ ( a ∨ b ) = a a\lor b =b\Rightarrow a\land b = a\land(a\lor b )=a a∨b=b⇒a∧b=a∧(a∨b)=a
引理2 通过L构造偏序集
在 [ L ; ∧ , ∨ ] [L;\land,\lor] [L;∧,∨]中, ∧ , ∨ \land,\lor ∧,∨满足4条运算规律,定义关系 ⪯ \preceq ⪯如下: ∀ a , b ∈ L , a ⪯ b \forall a,b \in L ,a\preceq b ∀a,b∈L,a⪯b,当且仅当 a ∨ b = b a\lor b =b a∨b=b.则 ( L ; ⪯ ) (L;\preceq) (L;⪯)为偏序集
证明自反性,反对称性,传递性 P211
定理3 引理2中的偏序集是格
证明 a ∨ b = l u b ( a , b ) , a ∧ b = g l b ( a , b ) a\lor b = lub(a,b),a\land b = glb(a,b) a∨b=lub(a,b),a∧b=glb(a,b) P211
定义4 格的另一种定义方式
[ L ; ∨ , ∧ ] [L;\lor,\land] [L;∨,∧]是一代数系统, ∨ , ∧ \lor,\land ∨,∧是定义在 L L L上的二元运算,当其满足 L 1 L_1 L1到 L 4 L_4 L4时,称 L L L为格,并称 ∧ \land ∧为积(交), ∨ \lor ∨为和(或并)
定理4 保序性
格 [ L ; ∨ , ∧ ] , ∀ a , b , c ∈ L [L;\lor,\land],\forall a,b,c\in L [L;∨,∧],∀a,b,c∈L,当 b ⪯ c b\preceq c b⪯c时有 a ∧ b ⪯ a ∧ c a\land b \preceq a\land c a∧b⪯a∧c及 a ∨ b ⪯ a ∨ c a\lor b\preceq a\lor c a∨b⪯a∨c
定义5 子格
[ L ; ∨ , ∧ ] [L;\lor,\land] [L;∨,∧]为格, T ≠ ∅ , T ⊆ L T\neq\varnothing,T\subseteq L T=∅,T⊆L, T T T关于 ∨ , ∧ \lor,\land ∨,∧封闭(即 a , b ∈ T , a ∨ b ∈ T , a ∧ b ∈ T a,b\in T,a\lor b \in T,a\land b \in T a,b∈T,a∨b∈T,a∧b∈T)时,称 T T T为 L L L的子格
注意,当 T T T为 L L L的子格时, T T T一定是格,但当 T ⊆ L T\subseteq L T⊆L, T T T关于 L L L中的偏序关系 ⪯ \preceq ⪯为格时, T T T不一定是 L L L的子格,因为 T T T中的运算关系可能不同
例如,一个群 G G G的子群全体 S ( G ) S(G) S(G)关于 ⊆ \subseteq ⊆关系所构成的格不是 G G G的幂集关于 ⊆ \subseteq ⊆关系所构成的格的子格,因为子群的并不一定是子群
定义6 格的同态与同构
设 [ L ; ∨ , ∧ ] [L;\lor,\land] [L;∨,∧]与 [ S ; + , ∘ ] [S;+,\circ] [S;+,∘]为两个格,如果存在映射 φ : L → S , ∀ a , b ∈ L \varphi:L\rightarrow S,\forall a,b\in L φ:L→S,∀a,b∈L,有
φ ( a ∧ b ) = φ ( a ) ∘ φ ( b ) φ ( a ∨ b ) = φ ( a ) + φ ( b ) \varphi(a\land b )=\varphi(a)\circ\varphi(b)\\ \varphi(a\lor b)=\varphi(a)+\varphi(b) φ(a∧b)=φ(a)∘φ(b)φ(a∨b)=φ(a)+φ(b)
则称 φ \varphi φ为 L L L到 S S S的同态映射,当 φ ( L ) = S \varphi(L)=S φ(L)=S时(满射),则说两个格同态,当 φ \varphi φ是一一对应(双射),说同构。如果 L = S L=S L=S,则称为自同态和自同构。
定理 5 同态映射是保序的
若 φ \varphi φ是格 L , S L,S L,S间的同态映射,则 φ \varphi φ是同态映射,即 ∀ a , b ∈ L \forall a,b\in L ∀a,b∈L,若 a ⪯ b a\preceq b a⪯b,则 φ ( a ) ⪯ φ ( b ) \varphi(a)\preceq\varphi(b) φ(a)⪯φ(b)注意不是当且仅当
定理6 同构映射的保序性
a ⪯ b ⟺ φ ( a ) ⪯ φ ( b ) a\preceq b \Longleftrightarrow \varphi(a)\preceq\varphi(b) a⪯b⟺φ(a)⪯φ(b)
定理7 对偶原理
- 设 P P P是对任意
偏序集都为真的一个命题, P ′ P' P′是将 P P P中所有 ⪯ , ⪰ \preceq,\succeq ⪯,⪰对换得到的对偶命题,则 P ′ P' P′对任意偏序集也为真 - 设 P P P是从格 [ B ; ∨ , ∧ ] [B;\lor,\land] [B;∨,∧]推出的命题, P ′ P' P′是将 P P P中 ∨ \lor ∨与 ∧ \land ∧对换得到的对偶命题,则 P ′ P' P′对格 [ B ; ∧ , ∨ ] [B;\land,\lor] [B;∧,∨]也为真
偏序反转后,自然从P得到了P‘
16.2 有补格及分配格
定义7 有界格
一个具有最大元1和最小元0的格 [ L ; ∨ , ∧ ] [L;\lor,\land] [L;∨,∧]称为有界格
定理8 最大元和最小元的性质
有界格中, ∀ a ∈ L : a ∨ 1 = 1 , a ∧ 0 = 0 , a ∧ 1 = a , a ∨ 0 = a \forall a\in L:a\lor 1 =1,a\land 0 =0,a\land 1 =a,a\lor 0 =a ∀a∈L:a∨1=1,a∧0=0,a∧1=a,a∨0=a
定义8 有补格
[ L ; ∨ , ∧ ] [L;\lor,\land] [L;∨,∧]为有界格,$\forall a \in L , 若 ,若 ,若\exist b\in L , 有 ,有 ,有a\lor b =1,a\land b =0 ,则称 ,则称 ,则称b 为 为 为a 的 ‘ 补元 ‘ , 记 的`补元`,记 的‘补元‘,记b 为 为 为a’ . 若 .若 .若L 中的每个元有补元,称 中的每个元有补元,称 中的每个元有补元,称L$为有补格
我们可以发现,对任意格成立分配不等式,即格 [ L ; ∨ , ∧ ] [L;\lor,\land] [L;∨,∧]中任意 a , b , c ∈ L a,b,c\in L a,b,c∈L,有:
- a ∨ ( b ∧ c ) ⪯ ( a ∨ b ) ∧ ( a ∨ c ) a\lor (b\land c)\preceq (a\lor b)\land(a\lor c) a∨(b∧c)⪯(a∨b)∧(a∨c)
- KaTeX parse error: Undefined control sequence: \and at position 34: …and c)\preceq a\̲a̲n̲d̲(b\lor c)
怎么说了,这个不等关系很容易记反,就画哈斯图吧
定义9 分配格
我们可以发现,对任意格成立分配不等式,即格 [ L ; ∨ , ∧ ] [L;\lor,\land] [L;∨,∧]中任意 a , b , c ∈ L a,b,c\in L a,b,c∈L,有:
- a ∨ ( b ∧ c ) = ( a ∨ b ) ∧ ( a ∨ c ) a\lor (b\land c)= (a\lor b)\land(a\lor c) a∨(b∧c)=(a∨b)∧(a∨c)
- KaTeX parse error: Undefined control sequence: \and at position 28: …or(a\land c)= a\̲a̲n̲d̲(b\lor c)
则称格L为分配格
两个典型的非分配格
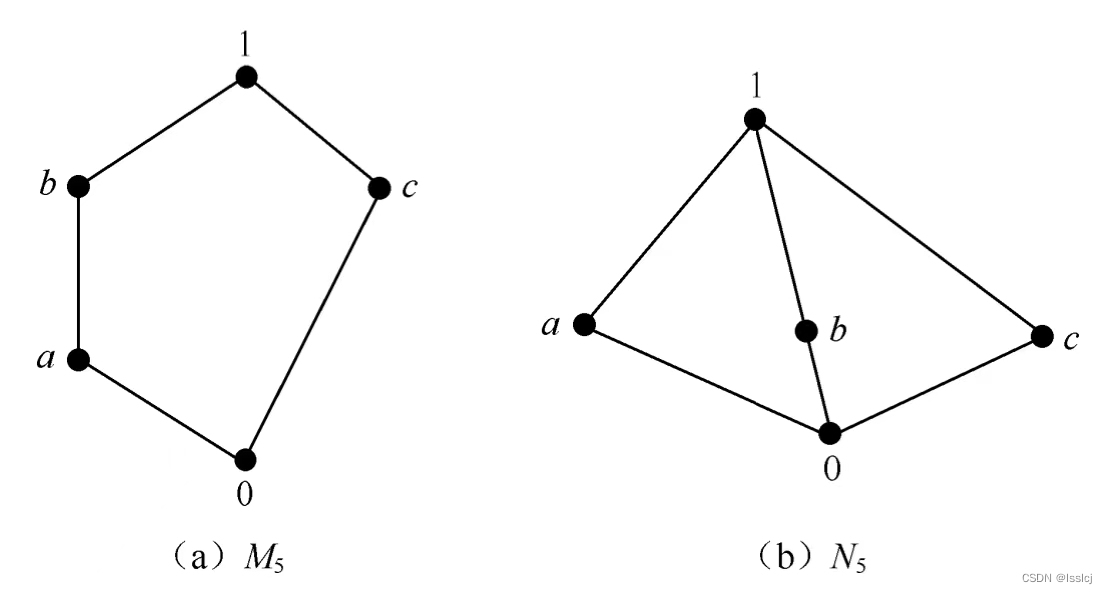
只要哈斯图中含有这种子结构,就可以判断它不是分配格
定理9 分配格的判断
[ L ; ∨ , ∧ ] [L;\lor,\land] [L;∨,∧]为任意格,则下述条件等价
- ∀ a , b , c ∈ L , a ∧ ( b ∨ c ) = ( a ∧ b ) ∨ ( a ∧ c ) \forall a,b,c\in L,a\land(b\lor c)=(a\land b)\lor(a\land c) ∀a,b,c∈L,a∧(b∨c)=(a∧b)∨(a∧c)
- ∀ a , b , c ∈ L , a ∨ ( b ∧ c ) = ( a ∨ b ) ∧ ( a ∨ c ) \forall a,b,c\in L,a\lor(b\land c)=(a\lor b)\land(a\lor c) ∀a,b,c∈L,a∨(b∧c)=(a∨b)∧(a∨c)
- ∀ a , b , c ∈ L , ( a ∧ b ) ∨ ( b ∧ c ) ∨ ( c ∧ a ) = ( a ∨ b ) ∧ ( b ∨ c ) ∧ ( c ∨ a ) \forall a,b,c\in L,(a\land b)\lor (b\land c)\lor(c\land a)=(a\lor b)\land(b\lor c)\land(c\lor a) ∀a,b,c∈L,(a∧b)∨(b∧c)∨(c∧a)=(a∨b)∧(b∨c)∧(c∨a)
- 不含 M 5 M_5 M5或 N 5 N_5 N5同构的子格
相关文章:

代数结构:5、格与布尔代数
16.1 偏序与格 偏序集:设P是集合,P上的二元关系“≤”满足以下三个条件,则称“≤”是P上的偏序关系(或部分序关系) (1)自反性:a≤a,∀a∈P; (2…...
如何使用DEEPL免费翻译PDF
如何使用DEEPL免费翻译PDF 安装DEEPL取消PDF限制 安装DEEPL 安装教程比较多,这里不重复。 把英文pdf拖进去,点翻译,在下面的框中有已经翻译完毕的文档。 但是存在两个问题 问题1:这些文档是加密的。 问题2:带有DeepL标…...

Spring-全面详解
Spring,就像是软件开发界的一个超级英雄,它让编写Java程序变得更简单、更灵活。想象一下,如果你要盖一栋大楼,Spring就是那个提供各种工具、框架和最佳实践的建筑大师,帮助你高效、优雅地搭建起整个项目。 Spring是啥&…...

QT自适应界面 处理高DPI 缩放比界面乱问题
1.pro文件添加 必须添加要不找不到 QT版本需要 5。4 以上才支持 QT widgets 2.main界面提前处理 // 1. 全局缩放使能QApplication::setAttribute(Qt::AA_EnableHighDpiScaling, true);// 2. 适配非整数倍缩放QGuiApplication::setHighDpiScaleFactorRoundingPolicy(Qt::High…...
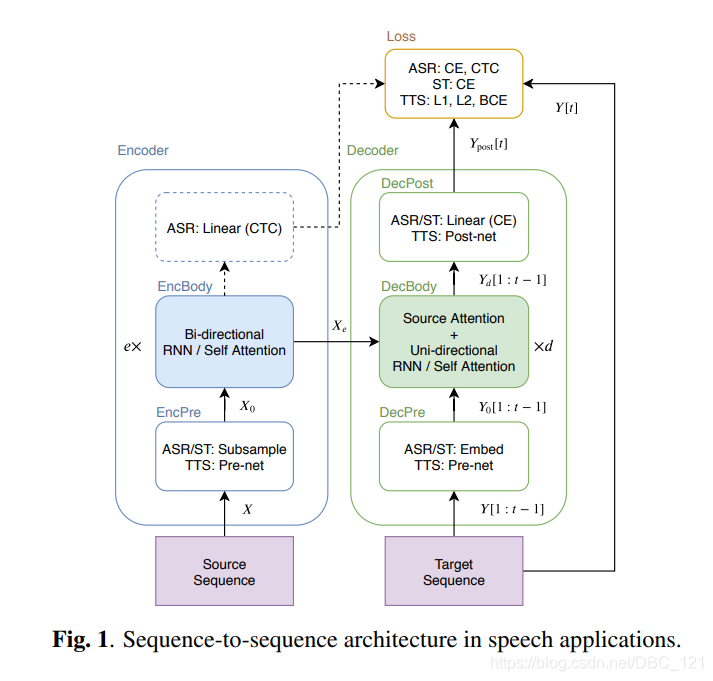
序列到序列模型在语言识别Speech Applications中的应用 Transformer应用于TTS Transformer应用于ASR 端到端RNN
序列到序列模型在语言识别Speech Applications中的应用 A Comparative Study on Transformer vs RNN in Speech Applications 序列到序列(Seq2Seq)模型在语音识别(Speech Applications)中有重要的应用。虽然Seq2Seq模型最初是为了解决自然语言处理中的序列生成问题而设计的…...
【Linux】- Linux环境变量[8]
目录 环境变量 $符号 自行设置环境变量 环境变量 环境变量是操作系统(Windows、Linux、Mac)在运行的时候,记录的一些关键性信息,用以辅助系统运行。在Linux系统中执行:env命令即可查看当前系统中记录的环境变量。 …...
前端笔记-day04
文章目录 01-后代选择器02-子代选择器03-并集选择器04-交集选择器05-伪类选择器06-拓展-超链接伪类07-CSS特性-继承性08-CSS特性-层叠性09-CSS特性-优先级11-Emmet写法12-背景图13-背景图平铺方式14-背景图位置15-背景图缩放16-背景图固定17-background属性18-显示模式19-显示模…...

计算机字符集产生的历史与乱码
你好,我是 shengjk1,多年大厂经验,努力构建 通俗易懂的、好玩的编程语言教程。 欢迎关注!你会有如下收益: 了解大厂经验拥有和大厂相匹配的技术等 希望看什么,评论或者私信告诉我! 文章目录 一…...
Rerank进一步提升RAG效果
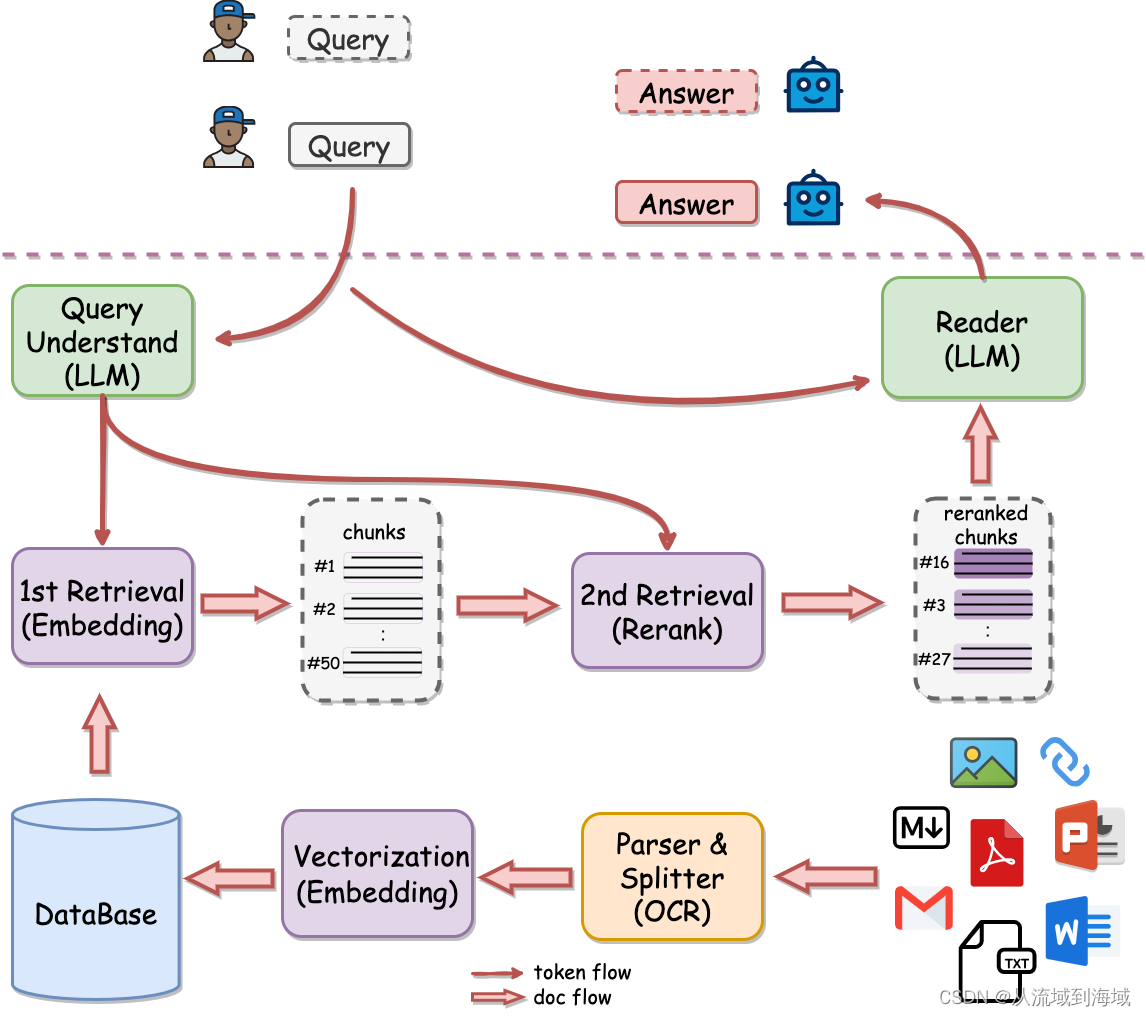
RAG & Rerank 目前大模型应用中,RAG(Retrieval Augmented Generation,检索增强生成)是一种在对话(QA)场景下最主要的应用形式,它主要解决大模型的知识存储和更新问题。 简述RAG without R…...

使用train.py----yolov7
准备工作 在训练之前,数据集的工作和配置环境的工作要做好 数据集:看这里划分数据集,训练自己的数据集。_划分数据集后如何训练-CSDN博客 划分数据集2,详细说明-CSDN博客 配置环境看这里 从0开始配置环境-yolov7_gpu0是inter g…...
机器学习第37周周报 GGNN
文章目录 week37 GGNN摘要Abstract一、文献阅读1. 题目2. abstract3. 网络架构3.1 数据处理部分3.2 门控图神经网络3.3 掩码操作 4. 文献解读4.1 Introduction4.2 创新点4.3 实验过程4.3.1 传感器设置策略4.3.2 数据集4.3.3 实验设置4.3.4 模型参数设置4.3.5 实验结果 5. 结论 …...
Baidu Comate:释放编码潜能,革新软件开发
Baidu Comate Baidu Comate,智能代码助手,凭借着文心大模型的强大支撑,结合了百度多年的编程实战数据和丰富的开源资源,形成了一款崭新的编码辅助利器。它不仅具备着高智能、多场景、价值创造的特质,更可广泛应用于各…...

MATLAB的Bar3函数调节渐变色(内附渐变色库.mat及.m文件免费下载链接)
一. colormap函数 可以使用colormap函数: t1[281.1,584.6, 884.3,1182.9,1485.2; 291.6,592.6,896,1197.75,1497.33; 293.8,596.4,898.6,1204.4,1506.4; 295.8,598,904.4,1209.0,1514.6];bar3(t1,1) set(gca,XTickLabel,{300,600,900,1200,1500},FontSize,10) set…...

使用 TensorFlow.js 和 OffscreenCanvas 实现实时防挡脸弹幕
首先,要理解我们的目标,我们将实时获取视频中的面部区域并将其周围的内容转为不透明以制造出弹幕的“遮挡效应”。 步骤一:环境准备 我们将使用 TensorFlow.js 的 Body-segmentation 库来完成面部识别部分,并使用 OffscreenCanv…...
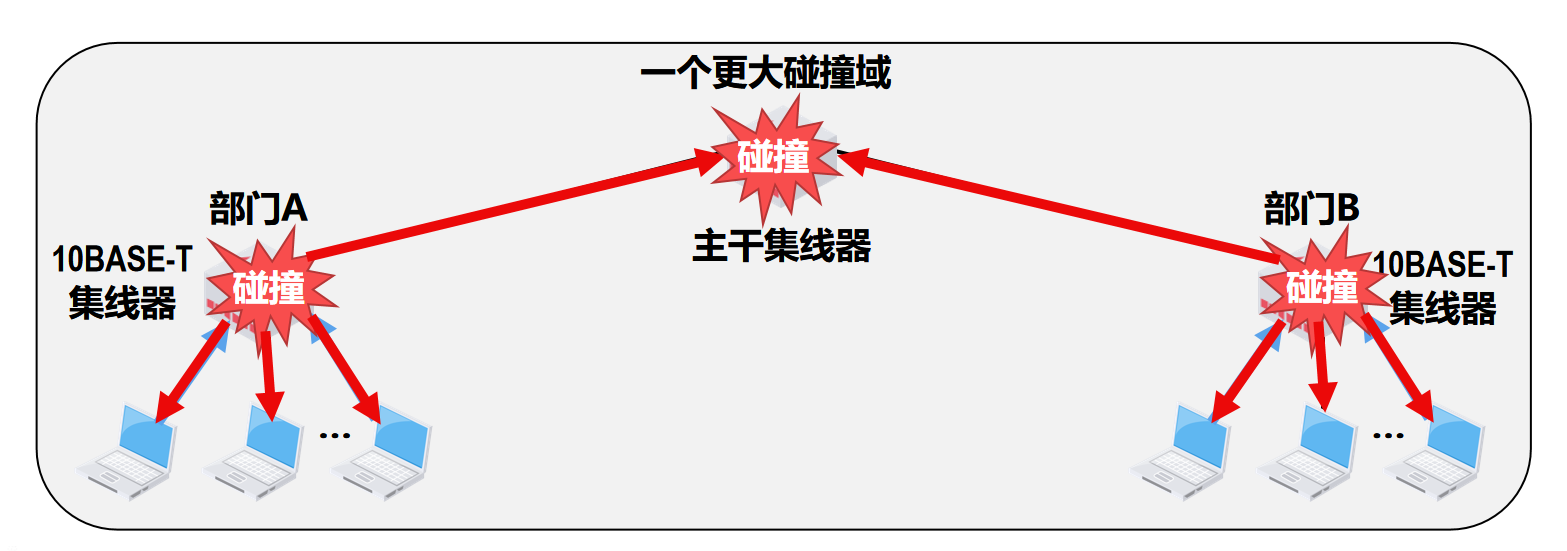
【计算机网络篇】数据链路层(10)在物理层扩展以太网
文章目录 🍔扩展站点与集线器之间的距离🛸扩展共享式以太网的覆盖范围和站点数量 🍔扩展站点与集线器之间的距离 🛸扩展共享式以太网的覆盖范围和站点数量 以太网集线器一般具有8~32个接口,如果要连接的站点数量超过了…...

conan2 基础入门(03)-使用(msvc为例)
conan2 基础入门(03)-使用(msvc为例) 文章目录 conan2 基础入门(03)-使用(msvc为例)⭐准备生成profile文件预备文件和Code ⭐使用指令预览正确执行结果可能出现的问题 ⭐具体讲解conanconanfile.txt执行 install cmakeCMakeLists.txt生成项目构建 END ⭐准备 在阅读和学习本文…...

uniapp this 作用域保持的方法
在 UniApp(或任何基于 Vue.js 的框架)中,this 关键字通常用于引用当前 Vue 实例的上下文。然而,当你在回调函数、定时器、Promise、异步函数等中使用 this 时,你可能会发现 this 的值不再指向你期望的 Vue 实例&#x…...

vue2 与vue3的差异汇总
Vue 2 与 Vue 3 之间存在多方面的差异,这些差异主要体现在性能、API设计、数据绑定、组件结构、以及生命周期等方面。以下是一些关键差异的汇总: 数据绑定与响应式系统 Vue 2 使用 Object.defineProperty 来实现数据的响应式,这意味着只有预…...
Java反射(含静态代理模式、动态代理模式、类加载器以及JavaBean相关内容)
目录 1、什么是反射 2、Class类 3、通过Class类取得类信息/调用属性或方法 4、静态代理和动态代理 5.类加载器原理分析 6、JavaBean 1、什么是反射 Java反射机制的核心是在程序运行时动态加载类并获取类的详细信息,从而操作类或对象的属性和方法。本质是JVM得…...

Scoop国内安装、国内源配置
安装配置源可参考gitee上的大佬仓库,里面的步骤、代码都很详细,实测速度也很好 glsnames/scoop-installer 也可以结合其它bucket使用 使用Github加速网站,也可以换做其他代理方式,自行测试 例如:https://mirror.ghprox…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...
 + 力扣解决)
LRU 缓存机制详解与实现(Java版) + 力扣解决
📌 LRU 缓存机制详解与实现(Java版) 一、📖 问题背景 在日常开发中,我们经常会使用 缓存(Cache) 来提升性能。但由于内存有限,缓存不可能无限增长,于是需要策略决定&am…...

STM32---外部32.768K晶振(LSE)无法起振问题
晶振是否起振主要就检查两个1、晶振与MCU是否兼容;2、晶振的负载电容是否匹配 目录 一、判断晶振与MCU是否兼容 二、判断负载电容是否匹配 1. 晶振负载电容(CL)与匹配电容(CL1、CL2)的关系 2. 如何选择 CL1 和 CL…...

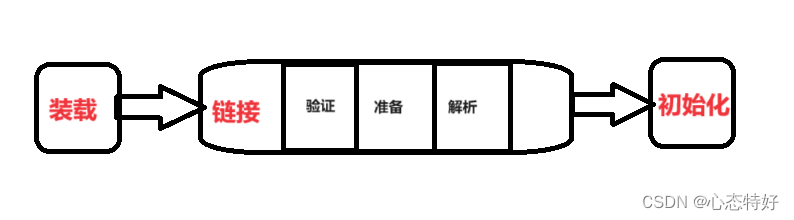
【从零开始学习JVM | 第四篇】类加载器和双亲委派机制(高频面试题)
前言: 双亲委派机制对于面试这块来说非常重要,在实际开发中也是经常遇见需要打破双亲委派的需求,今天我们一起来探索一下什么是双亲委派机制,在此之前我们先介绍一下类的加载器。 目录 编辑 前言: 类加载器 1. …...
