代码随想录Day 41|Leetcode|Python|198.打家劫舍 ● 213.打家劫舍II ● 337.打家劫舍III
198.打家劫舍
你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。
给定一个代表每个房屋存放金额的非负整数数组,计算你 不触动警报装置的情况下 ,一夜之内能够偷窃到的最高金额。
解题思路:
确定dp数组含义:dp[i]遍历到房屋index为i时所能打劫到的最多钱
确认递推公式:dp[i]取决于前一个房屋和前两个房屋是否有被偷,如果前一个被偷,则不能偷第i个,如果第i-2个被偷,可选择是否偷第i个。dp[i] = max(dp[i-2]+nums[i], dp[i-1])
初始化:dp[0] = nums[0], dp[1] = max(nums[0], nums[1])
遍历顺序:从小到大遍历
打印dp数组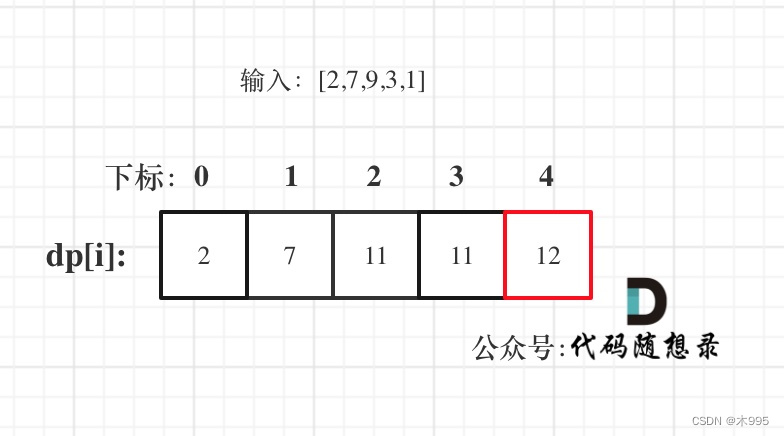
class Solution:def rob(self, nums: List[int]) -> int:if len(nums)<=1:return nums[0]dp = [0]*(len(nums))dp[0] = nums[0]dp[1] = max(nums[0], nums[1])for i in range(2, len(nums)):dp[i] = max(dp[i-2]+nums[i], dp[i-1])return dp[len(nums)-1]213.打家劫舍II
你是一个专业的小偷,计划偷窃沿街的房屋,每间房内都藏有一定的现金。这个地方所有的房屋都 围成一圈 ,这意味着第一个房屋和最后一个房屋是紧挨着的。同时,相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警 。
给定一个代表每个房屋存放金额的非负整数数组,计算你 在不触动警报装置的情况下 ,今晚能够偷窃到的最高金额。
解题思路:
本题与上一题区别在于环形数组和直线数组,环形数组首尾不能同时取值,因此分为三种情况:
- 不考虑首尾的数组
- 不考虑尾部的数组
- 不考虑首部的数组
可以发现2, 3包含情况一,因此只需要在2,3中取最大值即可。
dp五步骤:
确定dp数组含义:dp[i]遍历到房屋index为i时所能打劫到的最多钱
确认递推公式:dp[i]取决于前一个房屋和前两个房屋是否有被偷,如果前一个被偷,则不能偷第i个,如果第i-2个被偷,可选择是否偷第i个。dp[i] = max(dp[i-2]+nums[i], dp[i-1])
初始化:dp[0] = nums[0], dp[1] = max(nums[0], nums[1])
遍历顺序:从小到大遍历
打印dp数组
class Solution:def rob(self, nums: List[int]) -> int:if len(nums)<=1:return nums[0]def helper(subnums):if len(subnums)<=1:return subnums[0]dp = [0]*len(subnums)dp[0] = subnums[0]dp[1] = max(subnums[0], subnums[1])for i in range(2, len(subnums)):dp[i] = max(dp[i-2]+subnums[i], dp[i-1])print(dp)return dp[len(subnums)-1]return max(helper(nums[:-1]), helper(nums[1:]))337.打家劫舍III
小偷又发现了一个新的可行窃的地区。这个地区只有一个入口,我们称之为 root 。
除了 root 之外,每栋房子有且只有一个“父“房子与之相连。一番侦察之后,聪明的小偷意识到“这个地方的所有房屋的排列类似于一棵二叉树”。 如果 两个直接相连的房子在同一天晚上被打劫 ,房屋将自动报警。
给定二叉树的 root 。返回 在不触动警报的情况下 ,小偷能够盗取的最高金额 。
示例 1:
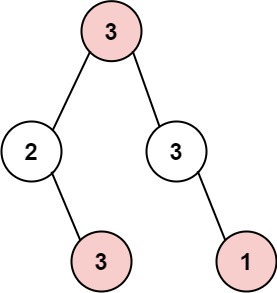
输入: root = [3,2,3,null,3,null,1] 输出: 7 解释: 小偷一晚能够盗取的最高金额 3 + 3 + 1 = 7
解题思路:
本体使用递归三部曲结合dp五步骤,设置dp[0],dp[1]表示打劫当前节点和不打劫当前节点的最大值,每个node有一组对应的dp[0], dp[1]。使用后序遍历,当前节点dp值需要结合其左右节点dp进行分析。 递归三步骤:确定递归参数,确定停止条件,递归逻辑。输入参数统一为当前节点即表示为root, 当root == null停止并返回0,再遍历左右子树,中间值取最大dp值。
重点理解
val1 = root.val + leftdp[0] + rightdp[0]#行窃root
val2 = max(leftdp[0],leftdp[1])+max(rightdp[0], rightdp[1])#不行窃root,选取左右子树行窃或不行窃时的最大值,两边取max。
代码如下:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:def rob(self, root: Optional[TreeNode]) -> int:def helper(root):if not root:return [0,0]leftdp = helper(root.left)rightdp = helper(root.right)val1 = root.val + leftdp[0] + rightdp[0]#行窃rootval2 = max(leftdp[0],leftdp[1])+max(rightdp[0], rightdp[1])#不行窃rootreturn [val2, val1]return max(helper(root))相关文章:

代码随想录Day 41|Leetcode|Python|198.打家劫舍 ● 213.打家劫舍II ● 337.打家劫舍III
198.打家劫舍 你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。 给定一个代表每个…...
【吴恩达机器学习-week2】多个变量的特征缩放和学习率问题
特征缩放和学习率(多变量) 目标 利用上一个实验中开发的多变量例程在具有多个特征的数据集上运行梯度下降探索学习率对梯度下降的影响通过 Z 分数归一化进行特征缩放,提高梯度下降的性能 import numpy as np np.set_printoptions(precisio…...

C#字符串的拼接
在C#中有多种拼接字符串的方式,今天小编就分享一些比较常用的。 方法1 string str "123"; str str "456"; 运行结果: "123456" 方法2 字符串与数字拼接 会将数字默认为字符串进行拼接 string str "123"; str str 1;…...

哈希表Hash table
哈希表是根据关键码的值而直接进行访问的数据结构。 数组就是⼀张哈希表。 哈希表中关键码就是数组的索引下标,然后通过下标直接访问数组中的元素,如下图所示: 那么哈希表能解决什么问题呢,一般哈希表都是用来快速判断⼀个元素是…...

jdk8新特性----Lambda表达式
一、介绍 1、简介 Java的Lambda表达式是Java 8引入的一个特性,它支持函数式编程,允许将函数作为方法的参数或返回值,从而简化了匿名内部类的使用,并提供了对并行编程的更好支持。 2、语法 Lambda表达式的使用前提是存在一…...
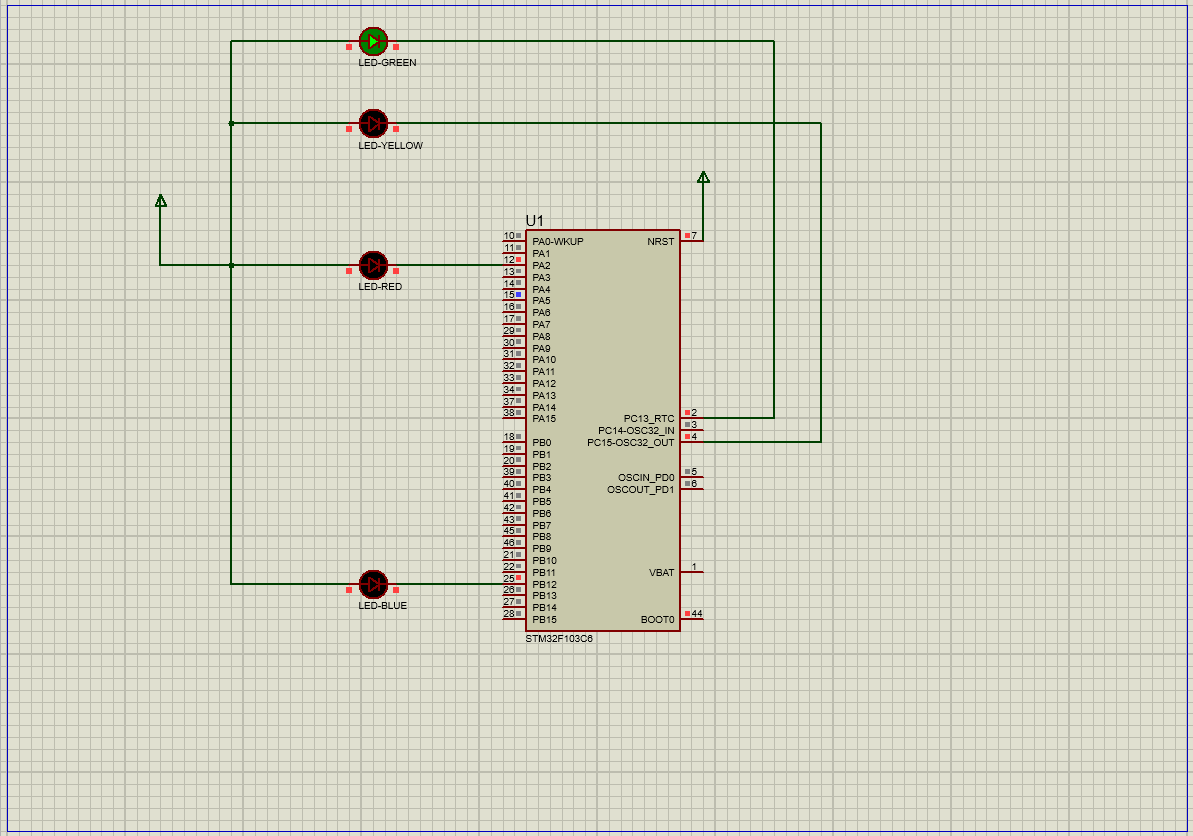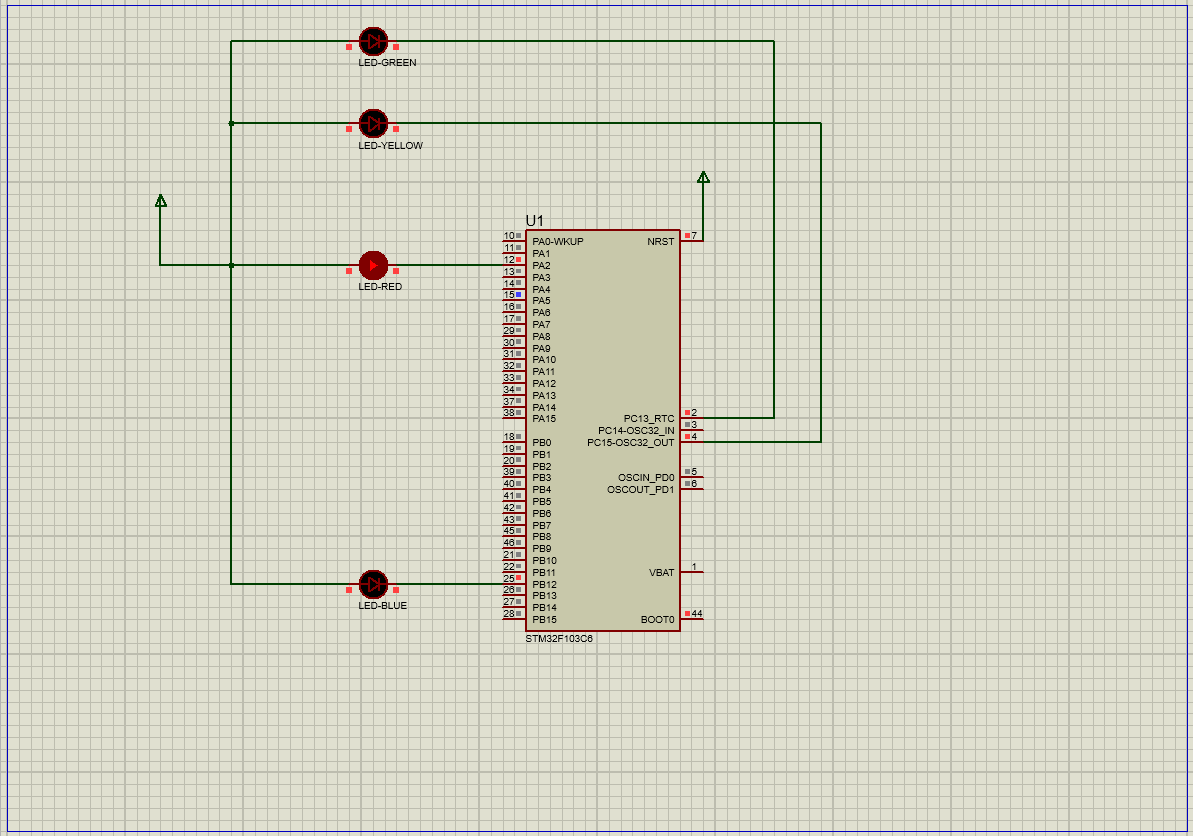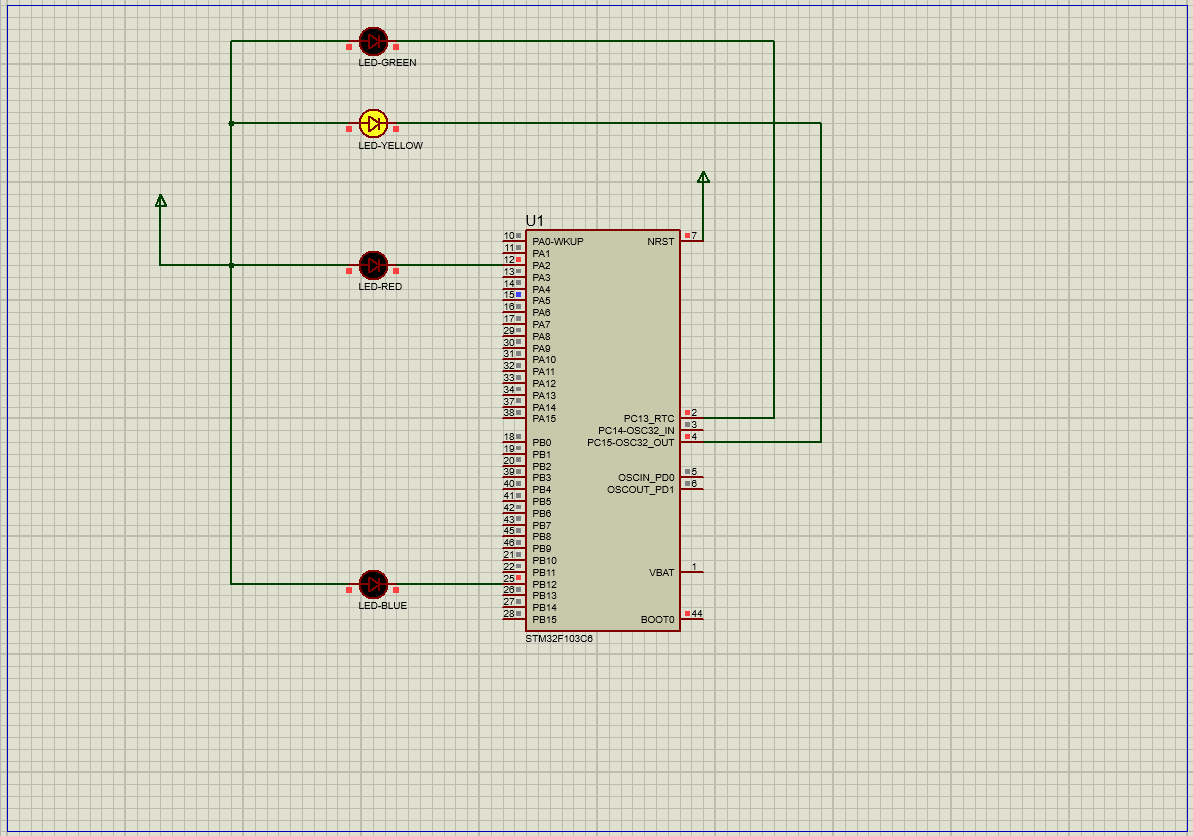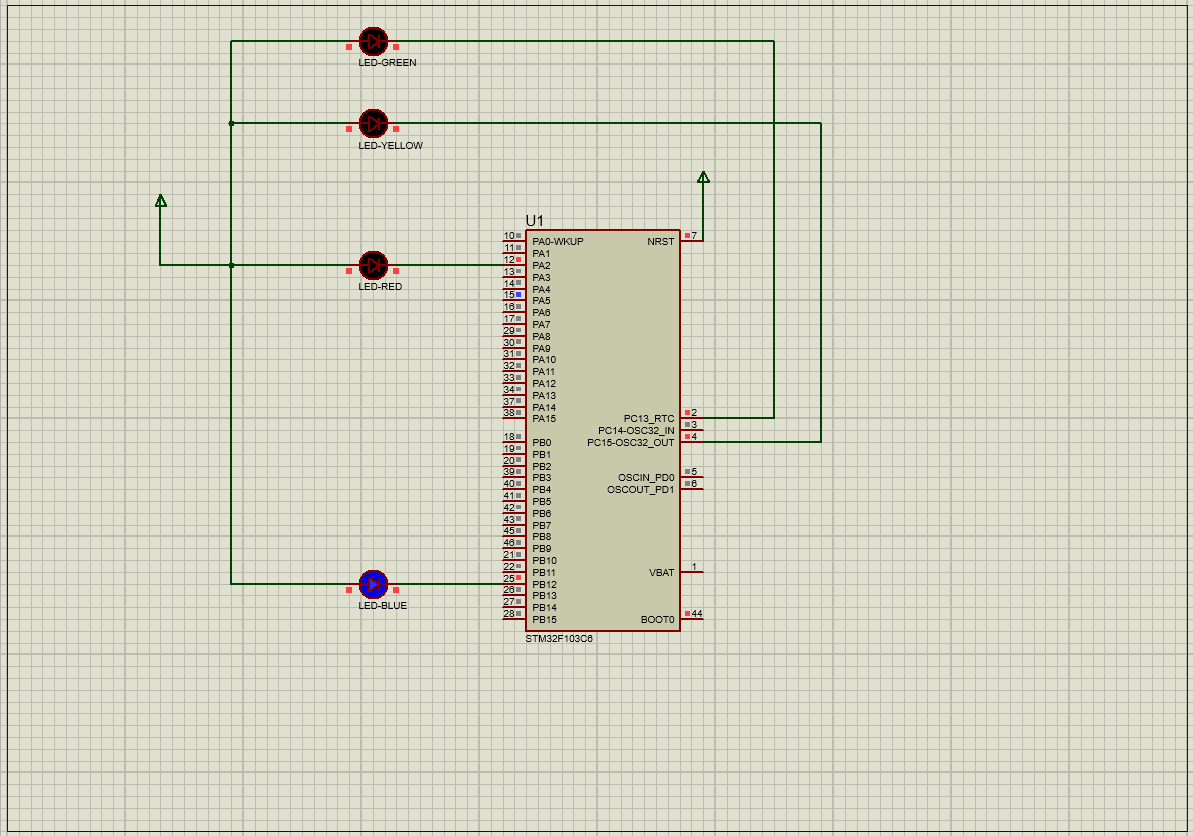
在STM32中用寄存器方式点亮流水灯
文章目录 实验资料一、对寄存器的理解1.通俗认识寄存器2.深入了解寄存器(1)端口配置低寄存器(配置0到7引脚的寄存器)(2)端口配置高寄存器(配置8到15引脚) 3.GPIO口的功能描述 二、配…...
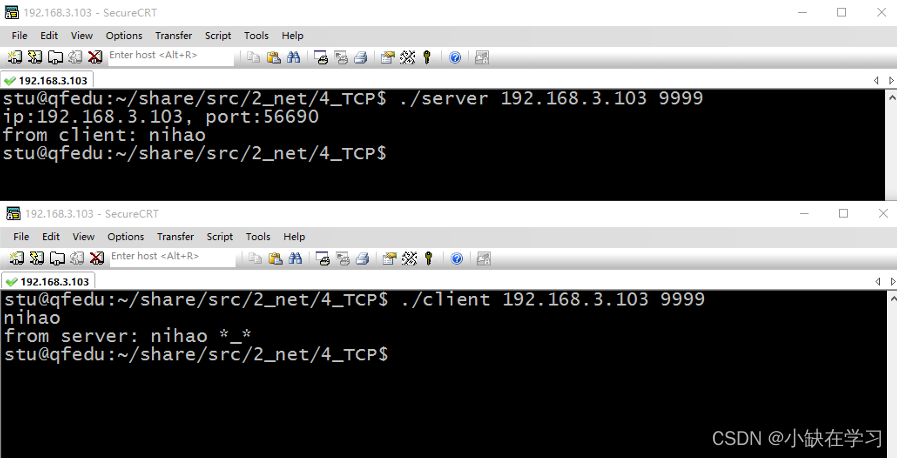
TCP(TCP客户端、服务器如何通信)
一、TCP介绍 TCP的特点: 面向连接的协议:TCP是一种可靠的、面向连接的协议,在通信之前需要建立连接,以确保数据的可靠传输。这意味着在传输数据之前,发送方和接收方之间需要建立一条可靠的连接通道。流式协议&#x…...
)
pdf 文件版面分析--PyMuPDF (python 文档解析提取)
1.介绍 PyMuPDF 和Fitz 是用于Python中处理PDF文件的相关模块。Fitz是P有MuPDF的字模块。提供一个简化和封装版本的P有MuPDF功能。 关系: PyMuPDF: 提供广泛的功能,用于操作PDF文档, 包括方便的高级函数与底层操作Fitz &#x…...

sql update 多表关联 inner join
当您需要更新一个表或者多个表中的数据,而多个表又存在关联时,可以使用 INNER JOIN 子句将多个表关联起来,并使用 SET更新。 格式如下: UPDATE table1 INNER JOIN table2 ON table1.column1 table2.column1 SET table1.column2…...

【OceanBase诊断调优】—— 租户资源统计项及其查询方法
本文主要介绍 OceanBase 数据库中租户资源统计项及其查询方法。 适用版本 OceanBase 数据库 V4.1.x、V4.2.x 版本。 CPU 资源统计项 逻辑 CPU 使用率(线程处理请求的时间占比)。 通过虚拟表 __all_virtual_sysstat 在 SYS 系统租户下,查看…...

【一键录音,轻松转换:用Python打造个性化音频记录工具】
在数字化时代,音频记录已成为日常学习、工作和娱乐不可或缺的一部分。想象一下,只需简单按下几个键,即可随时随地捕捉灵感,记录会议要点,或是珍藏孩子的童言稚语。本文将引领您步入Python编程的奇妙世界,展示如何借助几个强大的库,构建一个既简单又实用的音频录制及转换…...

Java类与对象(一)
类的定义与使用 在Java中使用关键字class定义一个类,格式如下: class 类名{// 成员变量/字段/属性//成员方法/行为 }Java中类和c语言中的结构体有点类似, 在Java中类名一般采用大驼峰(每个首字母大写)的形式…...

python中的装饰器,例子说明
在Python中,嵌套装饰器是指在一个函数上应用多个装饰器。每个装饰器都可以为函数添加一些特定的功能。以下是一个稍微复杂一些的例子,我们将创建一个记录日志和验证权限的嵌套装饰器。 ### 例子:记录日志和权限验证的嵌套装饰器 假设我们正…...

Leetcode经典题目之用队列实现栈
P. S.:以下代码均在VS2019环境下测试,不代表所有编译器均可通过。 P. S.:测试代码均未展示头文件stdio.h的声明,使用时请自行添加。 目录 1、题目展示2、题目分析3、完整代码演示4、结语 1、题目展示 前面我们了解过如何实现队列…...

DBSCAN聚类算法
目录 背景DBSCAN算法DBSCAN算法原理DBSCAN算法基本步骤DBSCAN算法调优DBSCAN算法优缺点参考文献 背景 如果有车队在某一片区域经常规律性作业,现在要让你来绘制这一片的路网,你会选择让一辆车从头到尾把所有路网跑一遍还是基于历史轨迹点通过技术手段构…...

【tauri】安装
https://blog.csdn.net/freewebsys/article/details/136092092 1 安装nodejs curl -sL https://deb.nodesource.com/setup_18.x -o nodesource_setup.sh sudo bash nodesource_setup.sh sudo apt install nodejs # 查看版本 node -v2 安装webkit2 sudo apt update sudo apt i…...

(Java)心得:LeetCode——19.删除链表的倒数第 N 个节点
一、原题 给你一个链表,删除链表的倒数第 n 个结点,并且返回链表的头结点。 示例 1: 输入:head [1,2,3,4,5], n 2 输出:[1,2,3,5]示例 2: 输入:head [1], n 1 输出:[]示例 3&…...
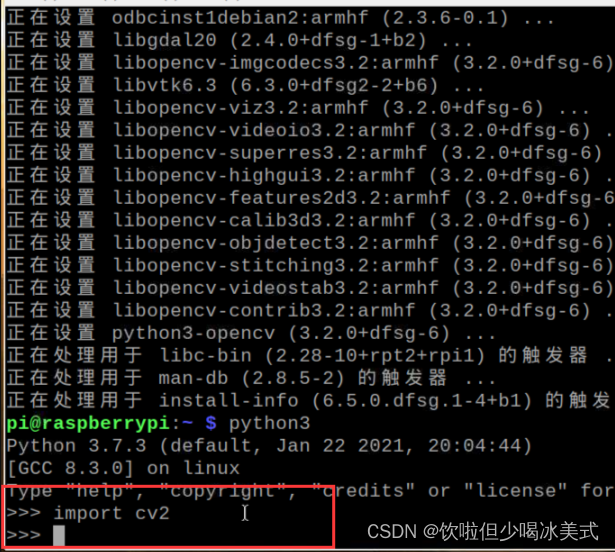
树莓派安装opencv
安装opencv 上述步骤完成后,输入以下代码(基于python3) sudo apt-get install python3-opencv -y不行的话,试试换源,然后 sudo apt-get update成功! 测试opencv是否安装成功 输入 python3 然后再输入 import cv2 没有报错就…...

bert 的MLM框架任务-梯度累积
参考:BEHRT/task/MLM.ipynb at ca0163faf5ec09e5b31b064b20085f6608c2b6d1 deepmedicine/BEHRT GitHub class BertConfig(Bert.modeling.BertConfig):def __init__(self, config):super(BertConfig, self).__init__(vocab_size_or_config_json_fileconfig.get(vo…...
Nginx配置/.well-known/pki-validation/
当你需要在Nginx上配置.well-known/pki-validation/时,这通常是为了支持SSL证书的自动续订或其他验证目的。以下是配置步骤: 创建目录结构: 在你的网站根目录下创建一个名为.well-known的目录(SSL证书申请之如何创建/.well-known/…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

宇树科技,改名了!
提到国内具身智能和机器人领域的代表企业,那宇树科技(Unitree)必须名列其榜。 最近,宇树科技的一项新变动消息在业界引发了不少关注和讨论,即: 宇树向其合作伙伴发布了一封公司名称变更函称,因…...

怎么让Comfyui导出的图像不包含工作流信息,
为了数据安全,让Comfyui导出的图像不包含工作流信息,导出的图像就不会拖到comfyui中加载出来工作流。 ComfyUI的目录下node.py 直接移除 pnginfo(推荐) 在 save_images 方法中,删除或注释掉所有与 metadata …...

Qt 事件处理中 return 的深入解析
Qt 事件处理中 return 的深入解析 在 Qt 事件处理中,return 语句的使用是另一个关键概念,它与 event->accept()/event->ignore() 密切相关但作用不同。让我们详细分析一下它们之间的关系和工作原理。 核心区别:不同层级的事件处理 方…...
