异常检测的学习和实战
1.应用:
1.在工业上的应用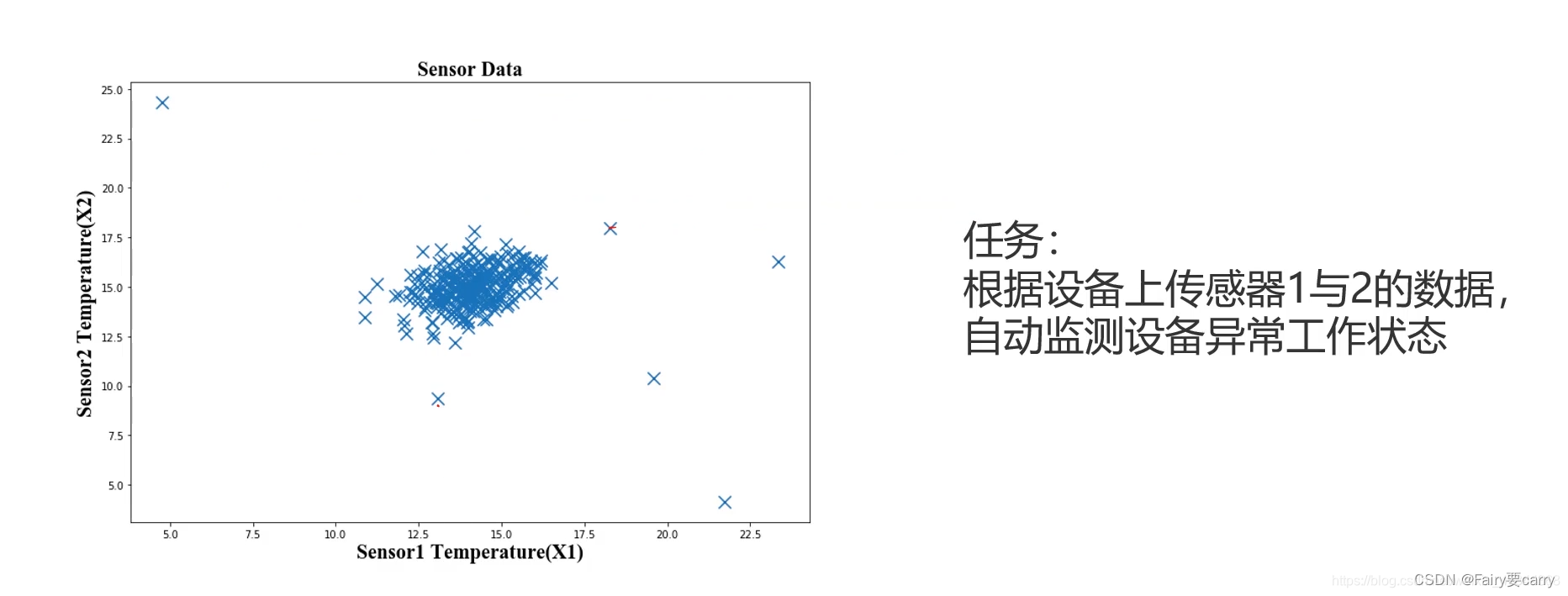
当检测设备是否处于异常工作状态时,可以由上图分析得到:那些零散的点对应的数据是异常数据。因为设备大多数时候都是处于正常工作状态的,所以数据点应该比较密集地集中在一个范围内,而那些明显偏出正常范围内的数据点就是我们要找的异常数据了,此时就可以自动
2.在图像里的应用
通过异常检测,我们也可以检测到图像中的异常图像。(如上图中的小红鱼)
此外,异常检测的应用还有很多,比如:
异常消费检测(商业)
缺陷基因检测(医疗)
劣质产品检测(工业)等等
2.对于异常检测的定义:
根据输入的数据,对不符合预期模式的数据进行识别
3.介绍:
假设我们有一个一维的数据集,在这个数据集中有m个样本: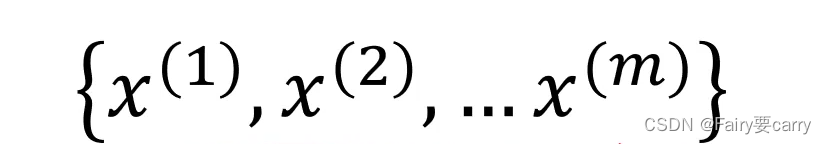
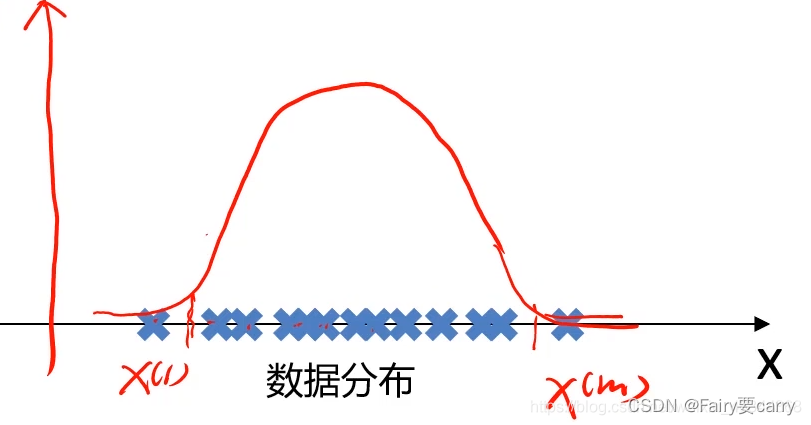
数据在x轴的分别如下图:

我们的目标是自动地找出这上面的异常样本,就可以根据样本在坐标轴上分布的数量多少,计算出坐标轴上各点对应的样本的概率密度,可以设定当概率密度小于某个值时,这时其对应的样本就是我们要找的异常样本。——>根据各个样本对应的概率函数计算出来的值画出数据分布,进而判断是否属于异常样本
这里说一下高斯分布的概率密度函数:

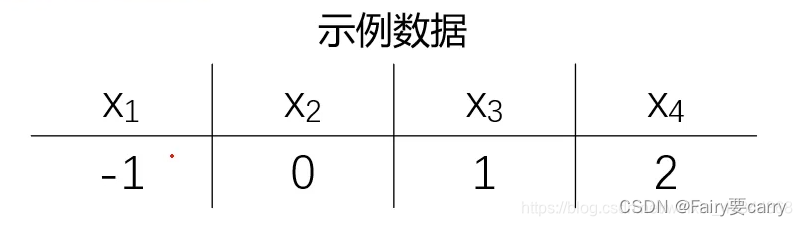
根据以上数据我们就可以计算出我们的均值和方差:
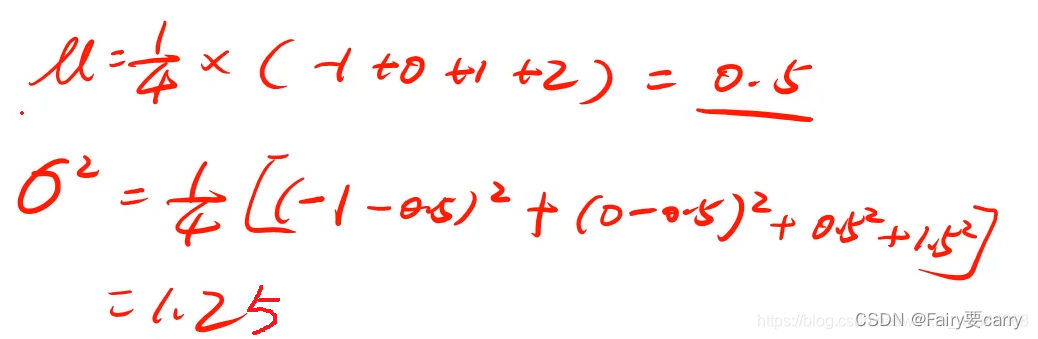
然后我们将均差和方差带入公式就能算出我们的P(x)了:
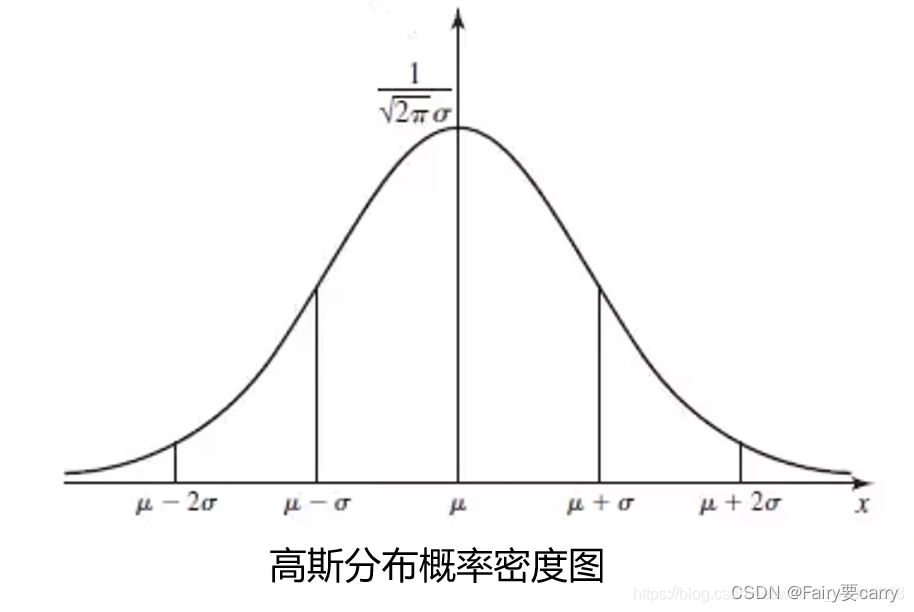
4.如何根据高斯分布概率去解决异常检测的问题呢?

**(第一步)**在我们知道X1、X2……Xm这些数据后,就可以进行相应计算了。
- 计算各个数据均值u,标准差σ
- 计算对应的高斯分布概率密度函数P(x)
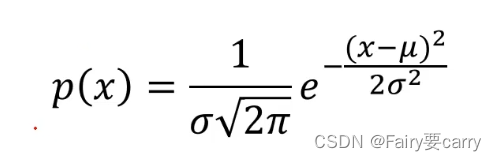
(第二步)计算出来后,数据对应的高斯分布概率密度函数如下图
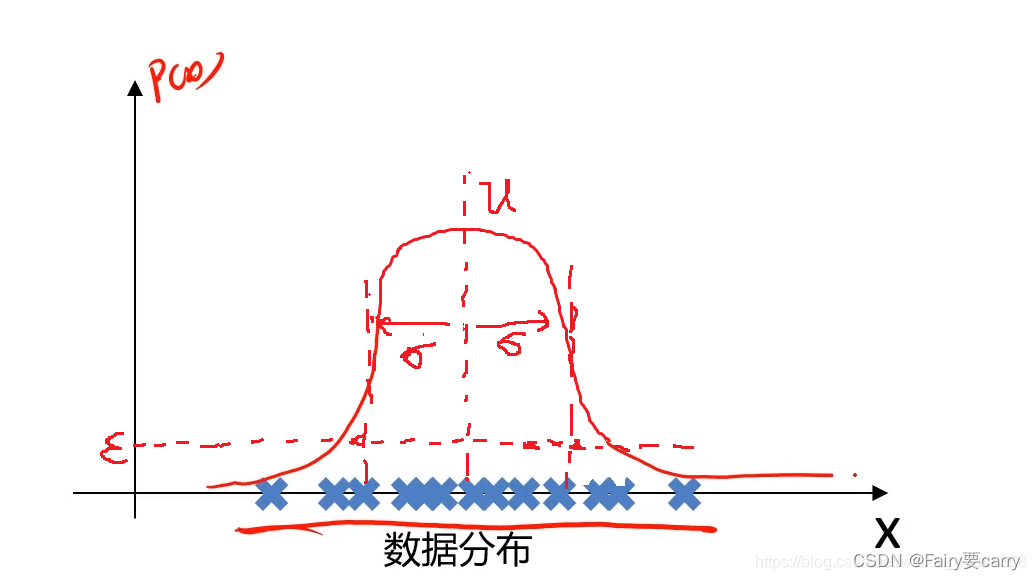
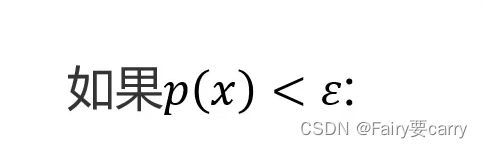 该点就为异常点
该点就为异常点
问:如果数据高于一维怎么办?
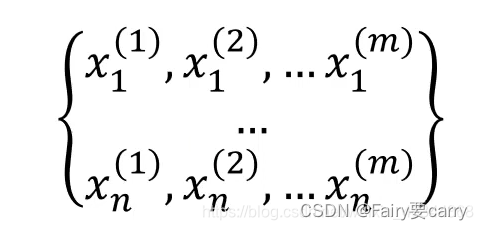
比如这里n维的数据,每一个维度都有m个样本。若要计算其高斯分布概率密度函数,可按如下步骤:
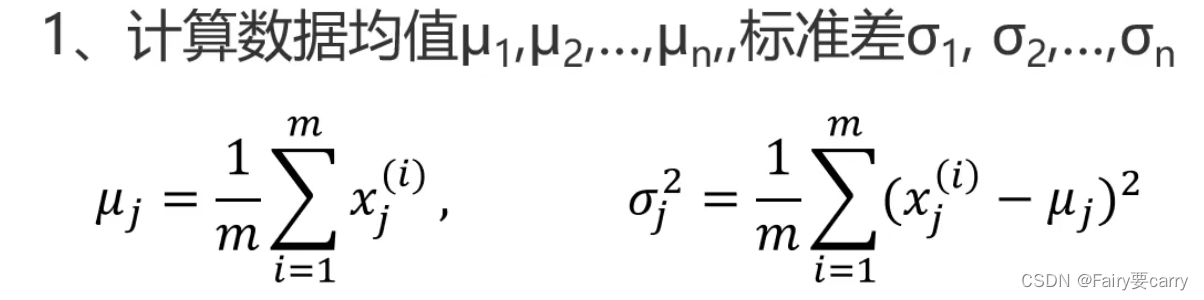 先计算出每一个维度下对应的均值和标准差了,这样就可以计算每个维度下的概率密度函数
先计算出每一个维度下对应的均值和标准差了,这样就可以计算每个维度下的概率密度函数

我们将计算出的每个维度下的概率密度函数相乘就可以计算出总的概率密度函数了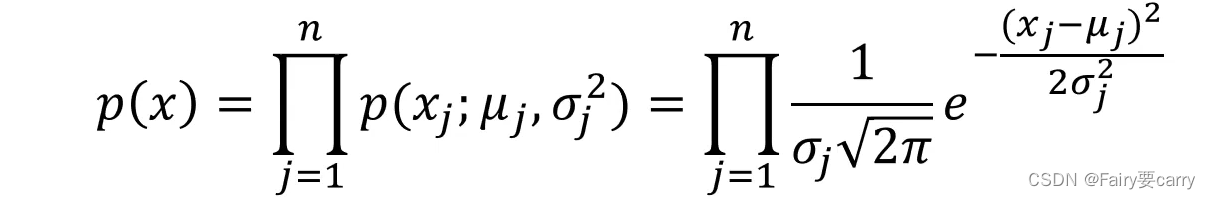
最后再根据高维下的概率密度函数判断其是否小于预期就可以判断异常点了
5.举个例子:
举个例子,下面给出一组二维数据,来判断当x1=3.5,x2=3.5时,对应的点是不是异常点
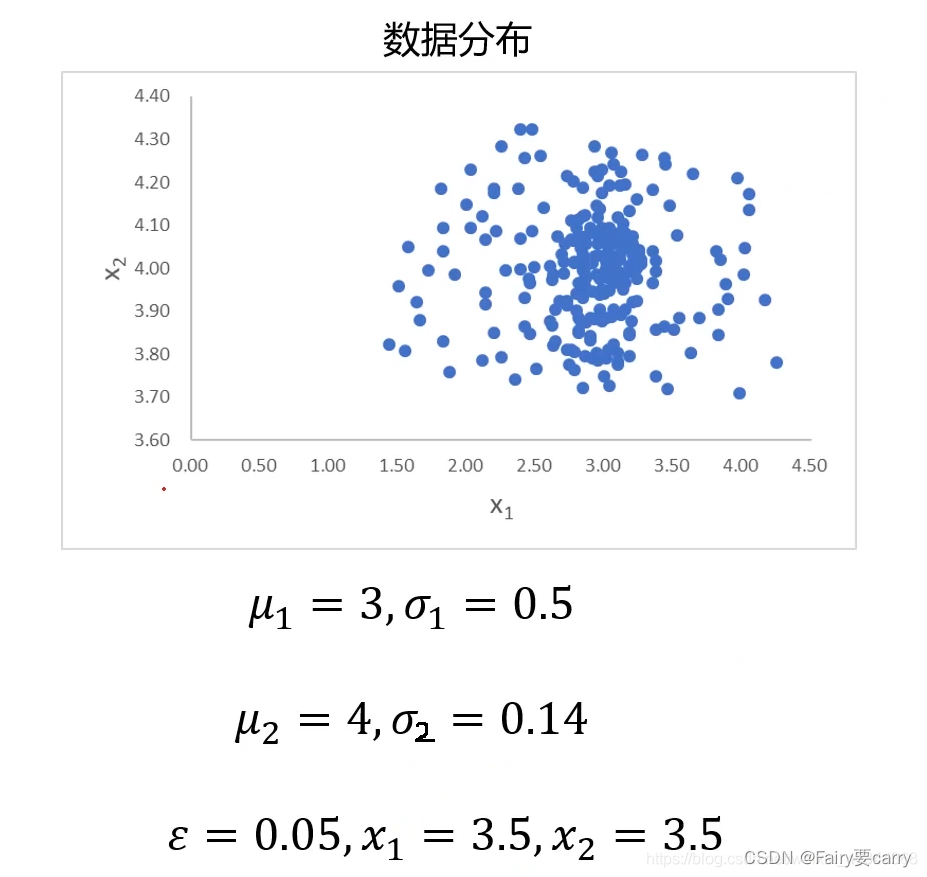
知道了标准差和均值,就可以计算其概率密度函数了
经计算可判断该点为异常点
很多时候,为了更直观的观察概率密度函数,我们是可以把它画出来的,下图是二维数据下的一个概率密度函数图
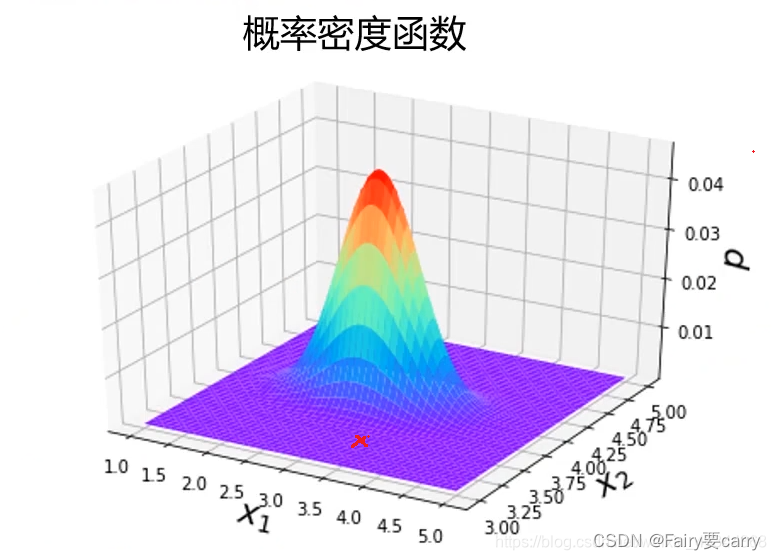
6.实战代码:
import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
import matplotlib as mlp # mlp设置字体
from scipy.stats import norm # norm计算高斯分布概率函数
from sklearn.covariance import EllipticEnvelope # EllipticEnvelope模型专门做异常检测的# 1.预览数据
data = pd.read_csv('D:/pythonDATA/anomaly_data.csv')
print(data.head())
# 2.进行数据分布可视化
fig1 = plt.figure(figsize=(10, 7))
x1 = data.loc[:, 'x1']
x2 = data.loc[:, 'x2']font2 = {'family': 'SimHei', 'weight': 'normal', 'size': '20'} # 定义一下字体(根据自己喜好定义即可)
mlp.rcParams['font.family'] = 'SimHei' # 设置字体
mlp.rcParams['axes.unicode_minus'] = False # 字符显示fig2 = plt.figure(figsize=(20, 7))plt.subplot(121) # 子图一行二列所属第一列(画x1)
plt.hist(x1, bins=100) # 分成100个数据分隔,即有100条条状图
plt.title('x1 数据分布统计', font2)
plt.xlabel('x1', font2)
plt.ylabel('出现次数', font2)plt.subplot(122) # 子图一行二列所属第二列(画x2)
plt.hist(x2, bins=100) # 分成100个数据分隔
plt.title('x2 数据分布统计', font2)
plt.xlabel('x2', font2)
plt.ylabel('出现次数', font2)
plt.show()# 3.计算x1、x2的均值(mean)和标准差(sigma)
print("计算x1,x2的mean均值和标准差sigma")
x1_mean = x1.mean()
x1_sigma = x1.std()
x2_mean = x2.mean()
x2_sigma = x2.std()
print(x1_mean, x1_sigma, x2_mean, x2_sigma)# 4.计算高斯分布概率密度函数
x1_range = np.linspace(0, 20, 300) # x1值得范围是0到20,300个点均分
x1_normal = norm.pdf(x1_range, x1_mean, x1_sigma) # 计算高斯分布概率密度函数x_normal
x2_range = np.linspace(0, 20, 300)
x2_normal = norm.pdf(x2_range, x2_mean, x2_sigma)# 5.可视化高斯分布概率密度函数
fig3 = plt.figure(figsize=(20, 7))
plt.subplot(121)
plt.plot(x1_range, x1_normal) # 可视化分布概率函数(x1的值切分做x,高斯分布概率函数作y)
plt.title('normal p(x1)')
plt.subplot(122)
plt.plot(x2_range, x2_normal) # 可视化分布概率函数(x2的值切分作为x轴,y轴为高斯分布概率函数)
plt.title('normal p(x2)')
plt.show()
# 6.建立模型
ad_model = EllipticEnvelope(contamination=0.03) # 默认阈值是0.1,我们修改为0.03观察变化
ad_model.fit(data)
# 7.预测
y_predict = ad_model.predict(data)
print(pd.value_counts(y_predict))
y_predict = np.array(y_predict)# 可视化结果
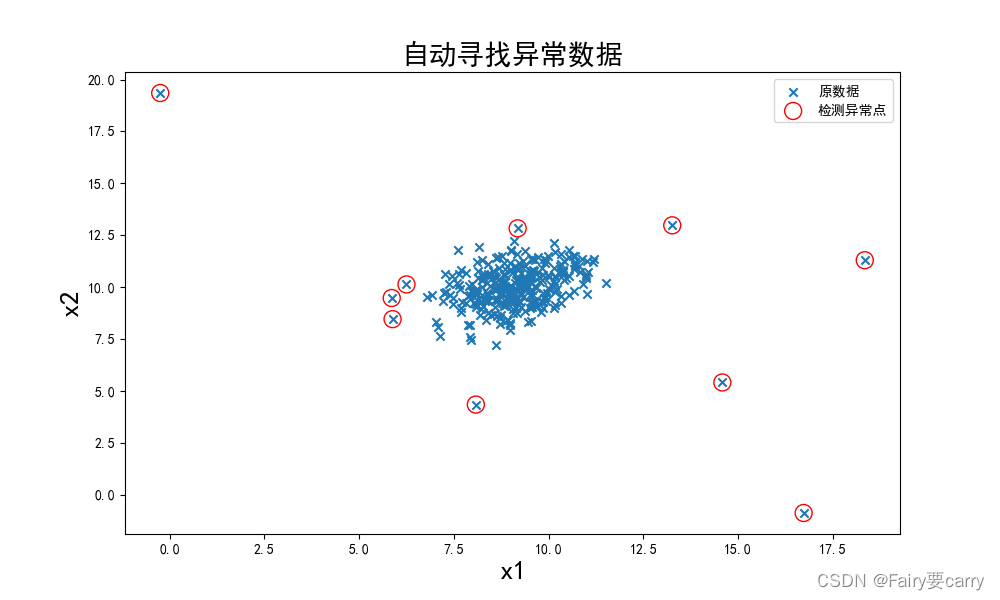
fig4 = plt.figure(figsize=(10, 6))
orginal_data = plt.scatter(data.loc[:, 'x1'], data.loc[:, 'x2'], marker='x') # 将各点用'x'表示
anomaly_data = plt.scatter(data.loc[:, 'x1'][y_predict == -1], data.loc[:, 'x2'][y_predict == -1], marker='o',facecolor='none', edgecolor='red', s=150)
# y_predict==-1即是异常点; marker='o'将异常点用圆圈圈起来; facecolor='none' 不填充,即空心圆; edgecolor='red' 颜色为红色; s=150 圆圈的大小.
plt.title('自动寻找异常数据', font2)
plt.xlabel('x1', font2)
plt.ylabel('x2', font2)
plt.legend((orginal_data, anomaly_data), ('原数据', '检测异常点'))
plt.show()数据分布图:
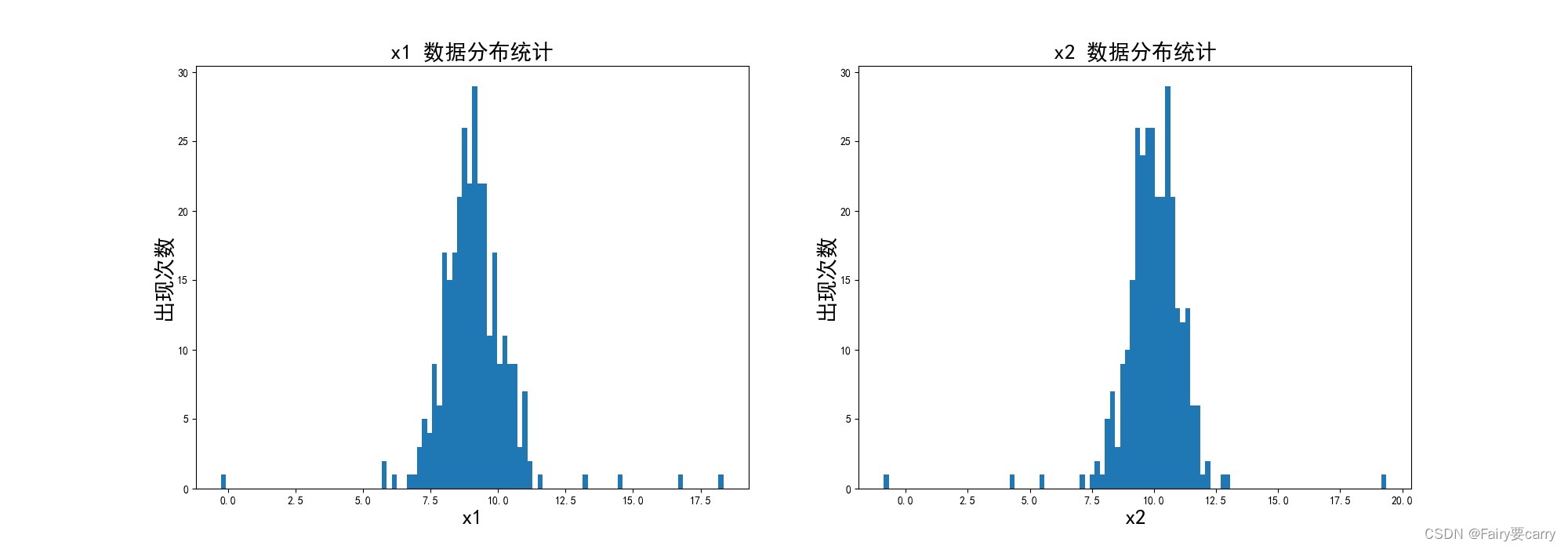
高斯概率分布图:
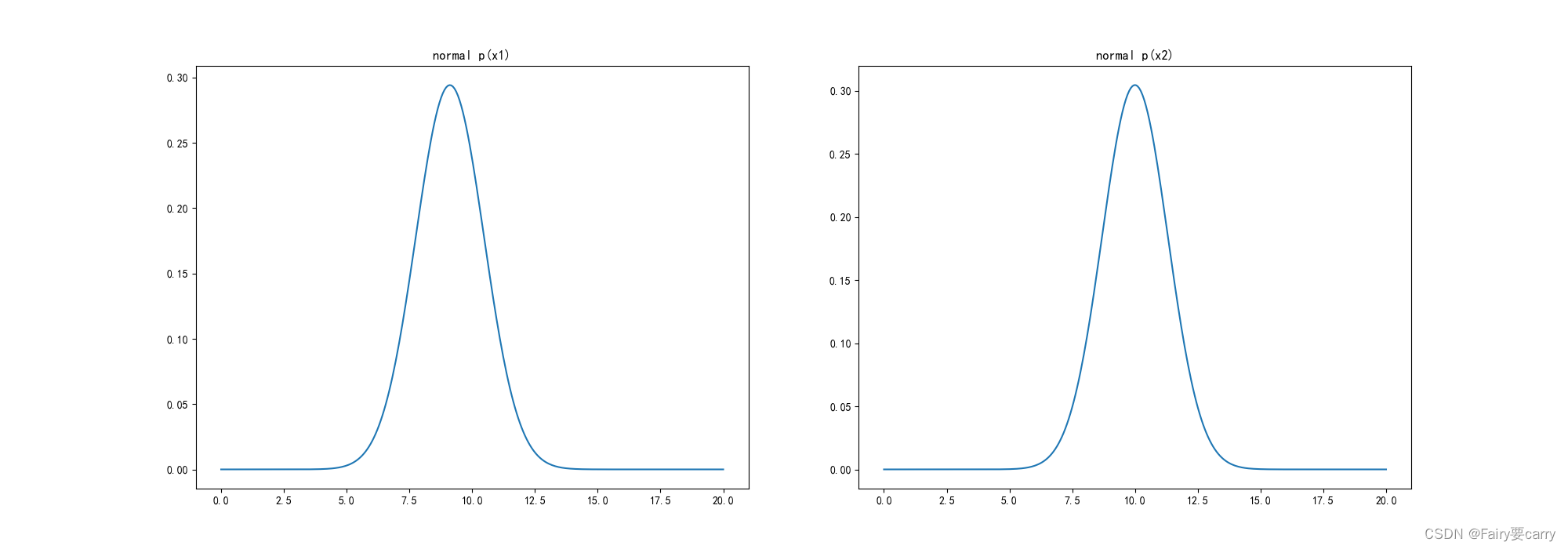
异常数据分布图:
相关文章:

异常检测的学习和实战
1.应用: 1.在工业上的应用 当检测设备是否处于异常工作状态时,可以由上图分析得到:那些零散的点对应的数据是异常数据。因为设备大多数时候都是处于正常工作状态的,所以数据点应该比较密集地集中在一个范围内,而那些明…...
)
RabbitMQ 面试题(一)
1. 简述为什么要使用 RabbitMQ ? 使用 RabbitMQ 的主要原因包括以下几点: 解耦:在复杂的系统中,不同的服务或组件之间往往需要通信和协作。RabbitMQ 作为消息队列,允许这些组件或服务通过发送和接收消息来交互,而无…...
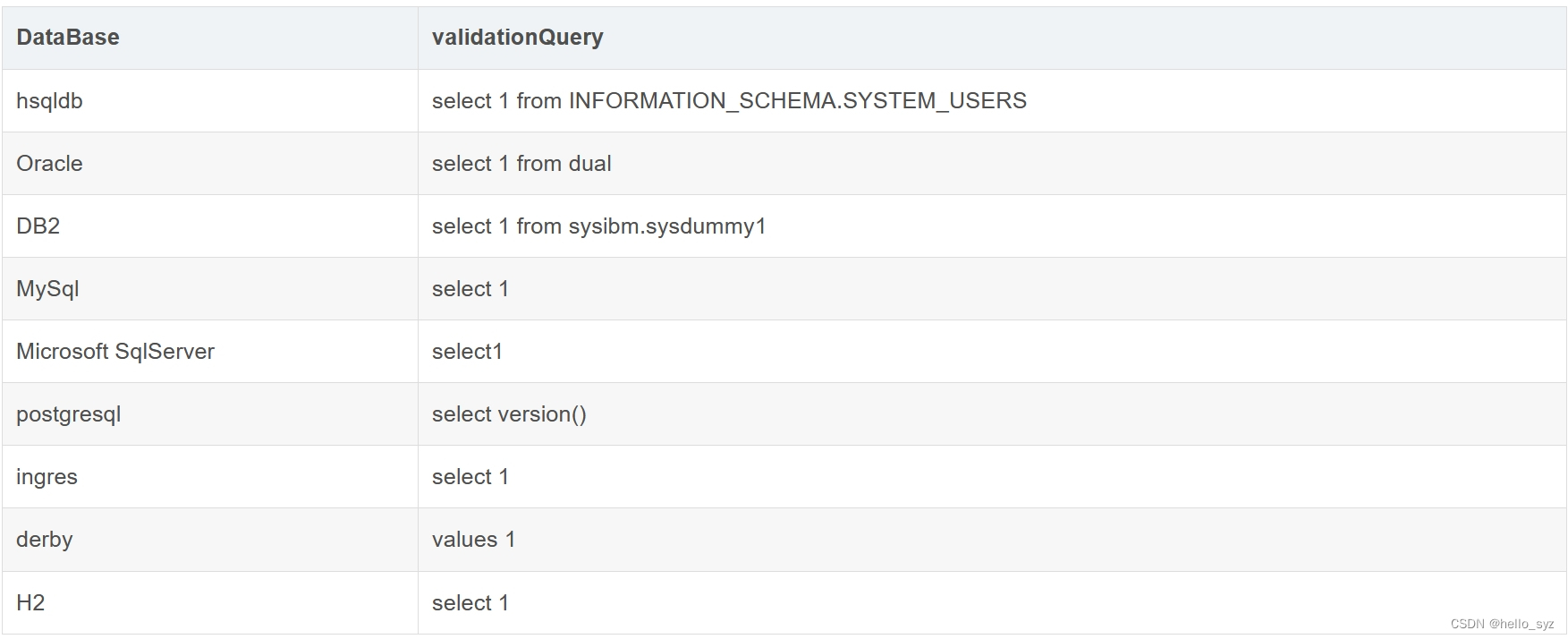
org.postgresql.util.PSQLException: 错误: 关系 “dual“ 不存在
springboot 项目连接 postgreps,启动时报错 org.postgresql.util.PSQLException: 错误: 关系 "dual" 不存在。 查阅资料后发现这是由配置文件中的配置 datasource-dynamic-druid-validationQuery 导致的 spring:datasource:druid:stat-view-servlet:ena…...

mysql权限分类
USAGE --无权限,只有登录数据库,只可以使用test或test_*数据库 ALL --所有权限 select/update/delete/super/slave/reload --指定的权限 with grant option --允许把自己的权限授予其它用户(此用户拥有建立账号的权限) 权限级别: 1、. --全…...
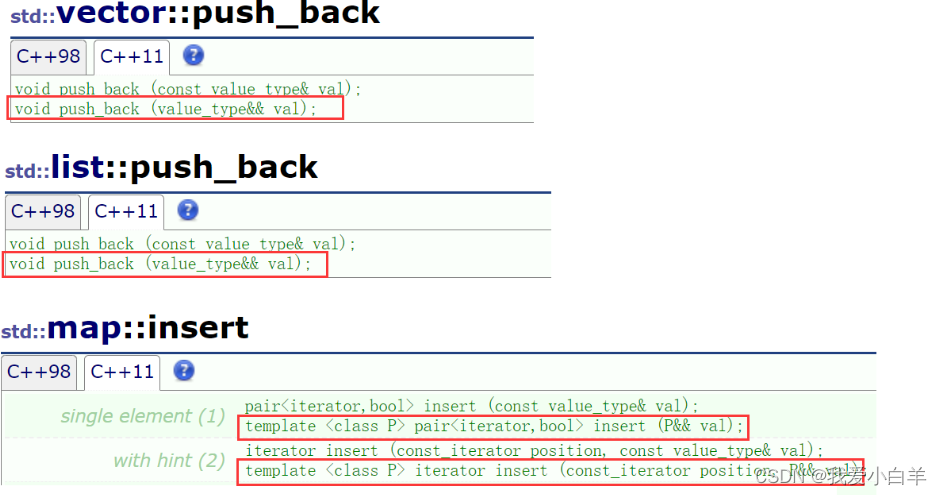
【C++11】列表初始化、右值引用的详细讲解(上)
前言 在一开始学C之前我们就简单的了解了一下C的发展历史。 相比较而言,C11能更好地用于系统开发和库开发、语法更加泛华和简单化、更加稳定和安全,不仅功能更强大,而且能提升程序员的开发效率加了许多特性,约140个新特性。使得C…...

【JAVA进阶篇教学】第十三篇:Java中volatile关键字讲解
博主打算从0-1讲解下java进阶篇教学,今天教学第十三篇:volatile关键字讲解。 在 Java 中,volatile关键字是一种轻量级的同步机制,用于确保变量的可见性和禁止指令重排序。本文将详细解释volatile关键字的工作原理、可见性保证以及…...

蓝桥杯-地宫取宝
X 国王有一个地宫宝库,是 nm 个格子的矩阵,每个格子放一件宝贝,每个宝贝贴着价值标签。 地宫的入口在左上角,出口在右下角。 小明被带到地宫的入口,国王要求他只能向右或向下行走。 走过某个格子时,如果那个…...
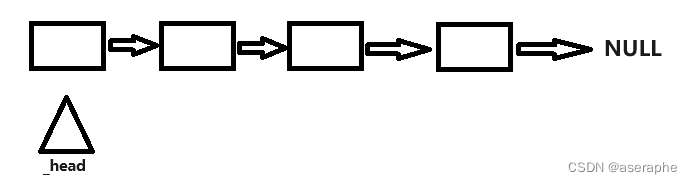
带头单链表 C++实现
节点定义 带头单链表:我们只需要一个结点指针指向整个链表的第一个节点,这样我们就可以通过next指针访问整个链表内的所有节点 template<class T> struct ListNode {T _val;ListNode* _next;ListNode(const T &val):_val(val),_next(nullptr){…...

学习c#第24天 枚举类型
using System; using System.Collections.Generic; using System.Linq; using System.Text; using System.Threading.Tasks; namespace enumType { //定义枚举 public enum Week { 星期一, 星期二, 星期三, 星期四, 星期…...

TensorFlow运行bug汇总
1、ImportError: urllib3 v2.0 only supports OpenSSL 1.1.1 解决方案 pip install urllib31.26.15 -i https://pypi.tuna.tsinghua.edu.cn/simple 升级或者降级 (TF2.1) C:\Users\Administrator>pip install urllib31.26.15 -i https://pypi.tuna.tsinghua.edu.cn/sim…...

docker部署调度程序
Dockerfile(构建初始镜像) # python:3.8-slim-buster为精简版的python FROM python:3.8-slim-buster # 1059为组的id,newgroup为组名,1088为用户的id,newuser为新用户 RUN groupadd -g 1059 newgroup && \useradd -g -u 1088 -g newgroup -m newuser USER newuser RUN…...

websocket和http协议的区别
ws(websocket)协议和http协议是两种不同的协议。 http:http是一种用于传输超文本的应用层协议,通常用于web端浏览器和web端服务器之间传输数据。http也是基于tcp的,但是HTTP只能在同一时刻单向发送消息,是一种半双工通信。&#…...

CSS之定位
目录 CSS定位为什么需要定位定位组成定位的叠放顺序拓展 CSS定位 为什么需要定位 浮动可以让多个块级盒子一行没有缝隙排列显示,经常用于横向排列盒子定位则是可以让盒子自由的在某个盒子内移动位置或者固定屏幕中的某个位置,并且可以压住其他盒子 定…...

[IM002][Microsoft][ODBC 驱动程序管理器] 未发现数据源名称并且未指定默认驱动程序
解决办法: 安装驱动 下载 ODBC Driver for SQL Server - ODBC Driver for SQL Server | Microsoft Learn...

神经网络复习--神经网络算法模型及BP算法
文章目录 神经网络模型的构成BP神经网络 神经网络模型的构成 三种表示方式: 神经网络的三要素: 具有突触或连接,用权重表示神经元的连接强度具有时空整合功能的输入信号累加器激励函数用于限制神经网络的输出 感知神经网络 BP神经网络 …...

【Java】/*方法的使用-快速总结*/
目录 一、什么是方法 二、方法的定义 三、实参和形参的关系 四、方法重载 五、方法签名 一、什么是方法 Java中的方法可以理解为C语言中的函数,只是换了个名称而已。 二、方法的定义 1. 语法格式: public static 返回类型 方法名 (形参列表) { //方…...

kotlin中协程相关
协程 用同步的方式写出异步的效果协程最重要的是通过非阻塞挂起和恢复实现了异步代码的同步编写方式挂起函数(suspend)不一定就是在子线程中执行的,但是通常在定义挂起函数时都会为它指定其他线程,这样挂起才有意义解决多层嵌套回调 协程不是线程&…...

(自适应手机端)物流运输快递仓储网站模板 - 带三级栏目
(自适应手机端)物流运输快递仓储网站模板 - 带三级栏目PbootCMS内核开发的网站模板,该模板适用于物流运输网站、仓储货运网站等企业,当然其他行业也可以做,只需要把文字图片换成其他行业的即可;自适应手机端,同一个后台…...
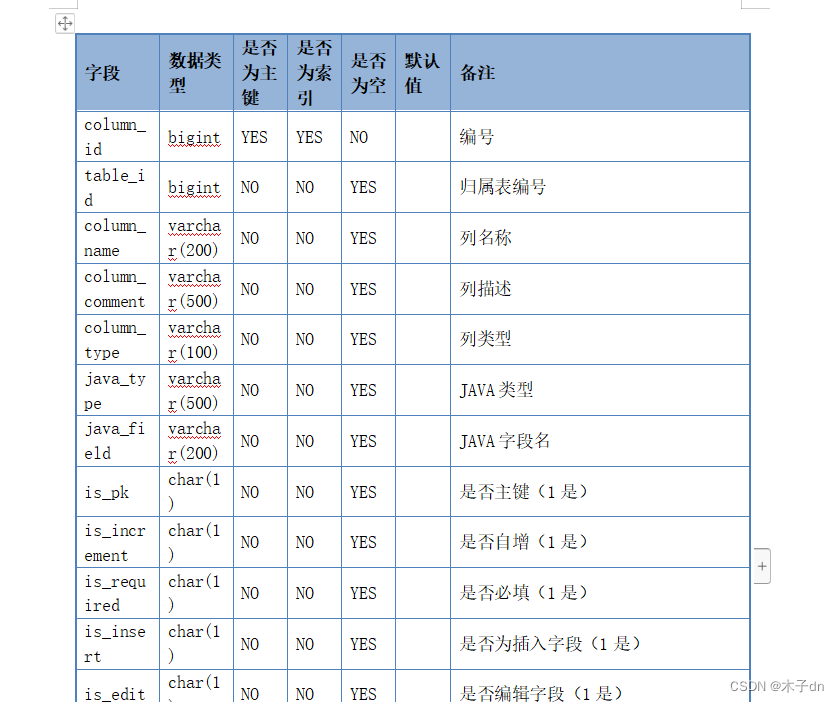
Navicat导出表结构到Excel或Word
文章目录 sql语句复制到excel复制到Word sql语句 SELECTcols.COLUMN_NAME AS 字段,cols.COLUMN_TYPE AS 数据类型,IF(pks.CONSTRAINT_TYPE PRIMARY KEY, YES, NO) AS 是否为主键,IF(idxs.INDEX_NAME IS NOT NULL, YES, NO) AS 是否为索引,cols.IS_NULLABLE AS 是否为空,cols.…...
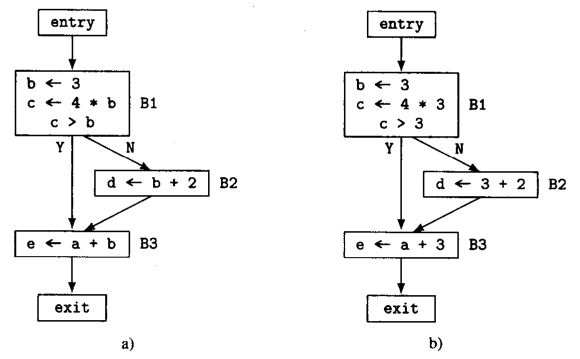
Golang编译优化——稀疏条件常量传播
文章目录 一、概述二、稀疏条件常量传播2.1 初始化worklist2.2 构建def-use链2.3 更新值的lattice2.4 传播constant值2.5 替换no-constant值 一、概述 常量传播(constant propagation)是一种转换,对于给定的关于某个变量 x x x和一个常量 c …...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

Java求职者面试指南:计算机基础与源码原理深度解析
Java求职者面试指南:计算机基础与源码原理深度解析 第一轮提问:基础概念问题 1. 请解释什么是进程和线程的区别? 面试官:进程是程序的一次执行过程,是系统进行资源分配和调度的基本单位;而线程是进程中的…...

Python Einops库:深度学习中的张量操作革命
Einops(爱因斯坦操作库)就像给张量操作戴上了一副"语义眼镜"——让你用人类能理解的方式告诉计算机如何操作多维数组。这个基于爱因斯坦求和约定的库,用类似自然语言的表达式替代了晦涩的API调用,彻底改变了深度学习工程…...
