蓝桥杯-地宫取宝
X 国王有一个地宫宝库,是 n×m 个格子的矩阵,每个格子放一件宝贝,每个宝贝贴着价值标签。
地宫的入口在左上角,出口在右下角。
小明被带到地宫的入口,国王要求他只能向右或向下行走。
走过某个格子时,如果那个格子中的宝贝价值比小明手中任意宝贝价值都大,小明就可以拿起它(当然,也可以不拿)。
当小明走到出口时,如果他手中的宝贝恰好是 k 件,则这些宝贝就可以送给小明。
请你帮小明算一算,在给定的局面下,他有多少种不同的行动方案能获得这 k 件宝贝。
输入格式
第一行 3 个整数,n,m,k,含义见题目描述。
接下来 n 行,每行有 m 个整数 Ci 用来描述宝库矩阵每个格子的宝贝价值。
输出格式
输出一个整数,表示正好取 k 个宝贝的行动方案数。
该数字可能很大,输出它对 1000000007 取模的结果。
数据范围
1≤n,m≤50,
1≤k≤12,
0≤Ci≤12
输入样例1:
2 2 2
1 2
2 1
输出样例1:
2
输入样例2:
2 3 2
1 2 3
2 1 5
输出样例2:
14
题解:
dp分析:
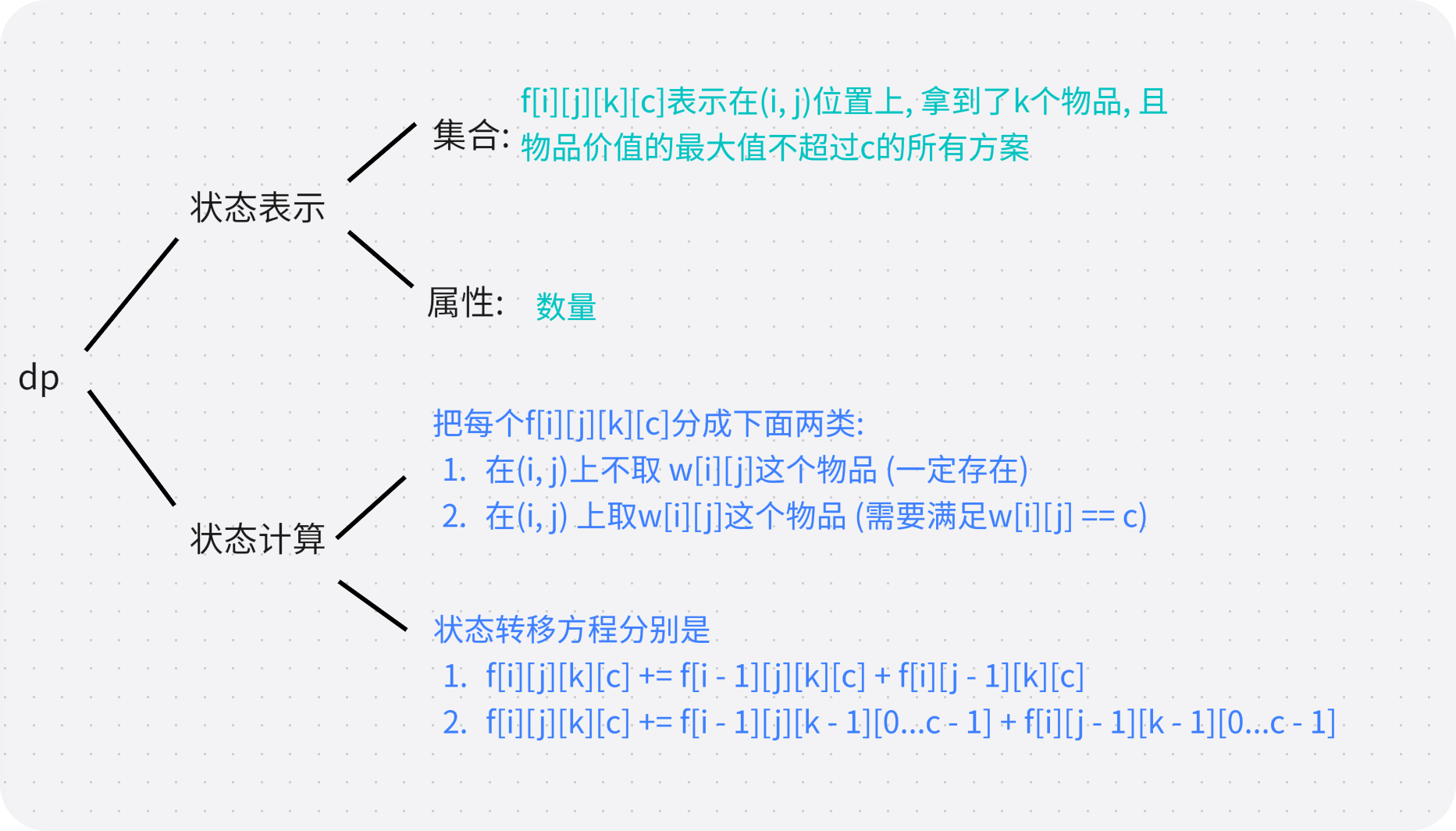
常见问题: 为什么取第(i,j)物品的时候要满足 c == w[i][j] ? 以及为什么状态转移方程2 为什么是0...c累加
- 我们原本定义了f[i][j][k][c]表示的是 在第(i, j)上的, 取了k个物品且这k个物品的最大值不超过c, 这里我们假设把f[i][j][k][c]表示成 在第(i, j)上的, 取了k个物品且这k个物品的最大值等于c, 这时候需要满足(w[i][j] == c)应该能理解吧。
- 那我们要想让我们假设的变成原本表示的含义, 需要让 f[i][j][k][c] 累加上 f[i][j][k][t] t要满足小于c, 这样我们f[i][j][k][c]表示的集合就从假设的变成了原本的, 但是如果f[i][j][k][c]不满足假设的含义, 那么我们没法让f[i][j][k][c]表示成原本的含义
- 所以取(i,j)上的物品是要满足(w[i][j]==c) 是为了能够更好的计算出正确含义的f[i][j][k][c]的值
Orz笔者是这么理解的~
详细的状态转移如下图:

注意事项:
我们f数组的第四维是代表 最大值不超过c, 但是题中 c = [0,12], 由于当我们没有选择任何一个物品的时候应该表示成-1, 但是下标没法是负的, 所以我们可以把每个 c 都加1, 也就是w[i][j] + 1. 这样我们 f 的第四维在没有取任何物品时就可以用 下标 0 表示了
看不懂的话, 可以先看这两个题, 摘花生 和 最长上升子序列, 本题是前两道题的揉和
ac代码👇
#include <bits/stdc++.h>
using namespace std;
const int N = 55, MOD = 1000000007;int w[N][N], n, m, k;
int f[N][N][13][14]; int main()
{cin >> n >> m >> k;for (int i = 1; i <= n; i ++)for (int j = 1; j <= m; j ++) cin >> w[i][j], w[i][j] ++;// 初始化f[1][1][1][w[1][1]] = 1; // 取f[1][1][0][0] = 1; // 不取for (int i = 1; i <= n; i ++)for (int j = 1; j <= m; j ++){if (i == 1 && j == 1) continue; // 初始话的跳过for (int u = 0; u <= k; u ++)for (int v = 0; v <= 13; v ++){f[i][j][u][v] = (f[i][j][u][v] + f[i][j - 1][u][v]) % MOD; // 状态计算 1f[i][j][u][v] = (f[i][j][u][v] + f[i - 1][j][u][v]) % MOD; // 状态计算 2if (u > 0 && w[i][j] == v) // u > 0 加不加都行, 不影响答案, 因为 u == 0的时候表示什么都没选, 进入下面的循环也没意义{for (int c = 0; c < v; c ++) // 常见问题解释的就是这里, 需要加上比 v 小的f, 才能让 f[i][j][k][c]表示的含义正确{f[i][j][u][v] = (f[i][j][u][v] + f[i][j - 1][u - 1][c]) % MOD; // 状态计算 3f[i][j][u][v] = (f[i][j][u][v] + f[i - 1][j][u - 1][c]) % MOD; // 状态计算 4}}}}int res = 0;for (int i = 0; i <= 13; i ++) res = (res + f[n][m][k][i]) % MOD;cout << res << endl;return 0;
}觉得写的不错的话, 点个赞吧~
相关文章:

蓝桥杯-地宫取宝
X 国王有一个地宫宝库,是 nm 个格子的矩阵,每个格子放一件宝贝,每个宝贝贴着价值标签。 地宫的入口在左上角,出口在右下角。 小明被带到地宫的入口,国王要求他只能向右或向下行走。 走过某个格子时,如果那个…...
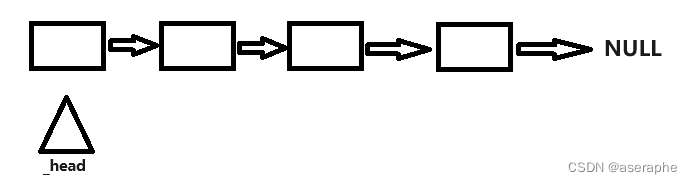
带头单链表 C++实现
节点定义 带头单链表:我们只需要一个结点指针指向整个链表的第一个节点,这样我们就可以通过next指针访问整个链表内的所有节点 template<class T> struct ListNode {T _val;ListNode* _next;ListNode(const T &val):_val(val),_next(nullptr){…...

学习c#第24天 枚举类型
using System; using System.Collections.Generic; using System.Linq; using System.Text; using System.Threading.Tasks; namespace enumType { //定义枚举 public enum Week { 星期一, 星期二, 星期三, 星期四, 星期…...

TensorFlow运行bug汇总
1、ImportError: urllib3 v2.0 only supports OpenSSL 1.1.1 解决方案 pip install urllib31.26.15 -i https://pypi.tuna.tsinghua.edu.cn/simple 升级或者降级 (TF2.1) C:\Users\Administrator>pip install urllib31.26.15 -i https://pypi.tuna.tsinghua.edu.cn/sim…...

docker部署调度程序
Dockerfile(构建初始镜像) # python:3.8-slim-buster为精简版的python FROM python:3.8-slim-buster # 1059为组的id,newgroup为组名,1088为用户的id,newuser为新用户 RUN groupadd -g 1059 newgroup && \useradd -g -u 1088 -g newgroup -m newuser USER newuser RUN…...

websocket和http协议的区别
ws(websocket)协议和http协议是两种不同的协议。 http:http是一种用于传输超文本的应用层协议,通常用于web端浏览器和web端服务器之间传输数据。http也是基于tcp的,但是HTTP只能在同一时刻单向发送消息,是一种半双工通信。&#…...

CSS之定位
目录 CSS定位为什么需要定位定位组成定位的叠放顺序拓展 CSS定位 为什么需要定位 浮动可以让多个块级盒子一行没有缝隙排列显示,经常用于横向排列盒子定位则是可以让盒子自由的在某个盒子内移动位置或者固定屏幕中的某个位置,并且可以压住其他盒子 定…...

[IM002][Microsoft][ODBC 驱动程序管理器] 未发现数据源名称并且未指定默认驱动程序
解决办法: 安装驱动 下载 ODBC Driver for SQL Server - ODBC Driver for SQL Server | Microsoft Learn...

神经网络复习--神经网络算法模型及BP算法
文章目录 神经网络模型的构成BP神经网络 神经网络模型的构成 三种表示方式: 神经网络的三要素: 具有突触或连接,用权重表示神经元的连接强度具有时空整合功能的输入信号累加器激励函数用于限制神经网络的输出 感知神经网络 BP神经网络 …...

【Java】/*方法的使用-快速总结*/
目录 一、什么是方法 二、方法的定义 三、实参和形参的关系 四、方法重载 五、方法签名 一、什么是方法 Java中的方法可以理解为C语言中的函数,只是换了个名称而已。 二、方法的定义 1. 语法格式: public static 返回类型 方法名 (形参列表) { //方…...

kotlin中协程相关
协程 用同步的方式写出异步的效果协程最重要的是通过非阻塞挂起和恢复实现了异步代码的同步编写方式挂起函数(suspend)不一定就是在子线程中执行的,但是通常在定义挂起函数时都会为它指定其他线程,这样挂起才有意义解决多层嵌套回调 协程不是线程&…...

(自适应手机端)物流运输快递仓储网站模板 - 带三级栏目
(自适应手机端)物流运输快递仓储网站模板 - 带三级栏目PbootCMS内核开发的网站模板,该模板适用于物流运输网站、仓储货运网站等企业,当然其他行业也可以做,只需要把文字图片换成其他行业的即可;自适应手机端,同一个后台…...
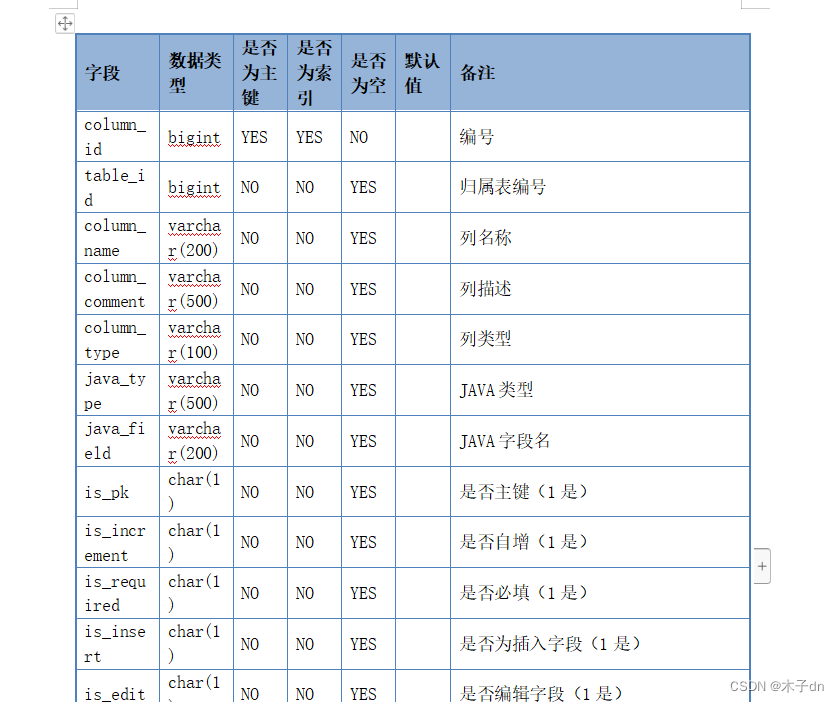
Navicat导出表结构到Excel或Word
文章目录 sql语句复制到excel复制到Word sql语句 SELECTcols.COLUMN_NAME AS 字段,cols.COLUMN_TYPE AS 数据类型,IF(pks.CONSTRAINT_TYPE PRIMARY KEY, YES, NO) AS 是否为主键,IF(idxs.INDEX_NAME IS NOT NULL, YES, NO) AS 是否为索引,cols.IS_NULLABLE AS 是否为空,cols.…...
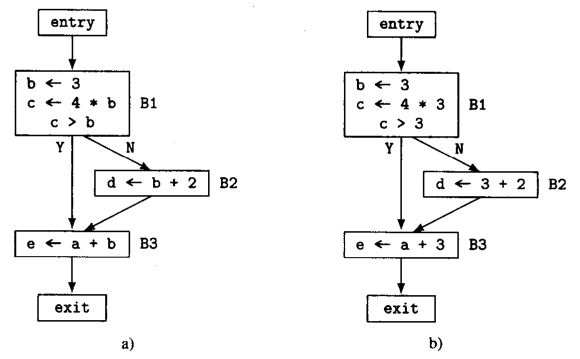
Golang编译优化——稀疏条件常量传播
文章目录 一、概述二、稀疏条件常量传播2.1 初始化worklist2.2 构建def-use链2.3 更新值的lattice2.4 传播constant值2.5 替换no-constant值 一、概述 常量传播(constant propagation)是一种转换,对于给定的关于某个变量 x x x和一个常量 c …...

人工智能培训讲师咨询叶梓介绍及智能医疗技术与ChatGPT临床应用三日深度培训提纲
1、授课老师简介 叶梓,上海交通大学计算机专业博士毕业,高级工程师。主研方向:数据挖掘、机器学习、人工智能。历任国内知名上市IT企业的AI技术总监、资深技术专家,市级行业大数据平台技术负责人。 长期负责城市信息化智能平台的…...
HCIP(BGP综合实验)--8
一:实验要求 二:实现过程 (一)配置IP地址: AR1: [AR1]int g0/0/0 [AR1-GigabitEthernet0/0/0]ip add 12.1.1.1 24 [AR1-GigabitEthernet0/0/0]int l0 [AR1-LoopBack0]ip add 172.16.0.1 32 [AR1-LoopBack0]int l1 […...

深入理解C++中的Vector容器:用容器构建高效程序
文章目录 vector介绍vector常用的成员函数有关vector定义的函数vector的迭代器使用vector关于空间操作的成员函数vector的增删查改 总结 vector介绍 在C语言的库中包含有公共数据结构的实现,C的这个部分内容就是众所周知的STL(标准模版库)&a…...
)
目标检测YOLO实战应用案例100讲-基于深度学习的交通场景多尺度目标检测算法研究与应用(下)
目录 3.2 基于空洞卷积的特征融合模块设计 3.3 改进k-means聚类算法的anchor尺寸优化设计...

react 类组件 和 函数组件 声明周期 对比
React 的类组件和函数组件在生命周期方面存在一些差异。以下是它们之间的对比: 类组件的生命周期 React 类组件的生命周期可以分为三个阶段:挂载、更新和卸载。 1、挂载阶段: constructor():组件实例化时调用,用于…...
智慧变电站守护者:TSINGSEE青犀AI视频智能管理系统引领行业革新
一、方案概述 随着科技的不断进步,人工智能(AI)技术已经深入到各个领域。在变电站安全监控领域,引入AI视频监控智能分析系统,可以实现对站内环境、设备状态的实时监控与智能分析,从而提高变电站的安全运行…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...

人工智能 - 在Dify、Coze、n8n、FastGPT和RAGFlow之间做出技术选型
在Dify、Coze、n8n、FastGPT和RAGFlow之间做出技术选型。这些平台各有侧重,适用场景差异显著。下面我将从核心功能定位、典型应用场景、真实体验痛点、选型决策关键点进行拆解,并提供具体场景下的推荐方案。 一、核心功能定位速览 平台核心定位技术栈亮…...

Linux安全加固:从攻防视角构建系统免疫
Linux安全加固:从攻防视角构建系统免疫 构建坚不可摧的数字堡垒 引言:攻防对抗的新纪元 在日益复杂的网络威胁环境中,Linux系统安全已从被动防御转向主动免疫。2023年全球网络安全报告显示,高级持续性威胁(APT)攻击同比增长65%,平均入侵停留时间缩短至48小时。本章将从…...

开疆智能Ethernet/IP转Modbus网关连接鸣志步进电机驱动器配置案例
在工业自动化控制系统中,常常会遇到不同品牌和通信协议的设备需要协同工作的情况。本案例中,客户现场采用了 罗克韦尔PLC,但需要控制的变频器仅支持 ModbusRTU 协议。为了实现PLC 对变频器的有效控制与监控,引入了开疆智能Etherne…...

Caliper 配置文件解析:config.yaml 和 fisco-bcos.json 附加在caliper中执行不同的合约方法
Caliper 配置文件解析:config.yaml 和 fisco-bcos.json Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO…...

PublishSubject、ReplaySubject、BehaviorSubject、AsyncSubject的区别
python容易编辑,因此用pyrx代替rxjava3做演示会比较快捷。 pyrx安装命令: pip install rx 一、Subject(相当于 RxJava 的 PublishSubject) PublishSubject PublishSubject 将对观察者发送订阅后产生的元素,而在订阅前…...

C语言内存管理和编译优化实战
参考: C语言内存管理“玄学”:从崩溃到精通的避坑指南C语言编译优化实战:从入门到进阶的高效代码优化技巧...
