单调栈问题
原理
单调栈的核心原理是:在栈内保持元素的单调性(递增或递减)
单调递增栈:
用于处理“下一个更小的元素”问题。当新元素比栈顶元素小或等于时,直接入栈;否则,一直从栈顶弹出元素,直到栈顶元素小于新元素或栈为空。
单调递减栈:
用于处理“下一个更大的元素”问题。当新元素比栈顶元素大时,一直从栈顶弹出元素,直到栈顶元素大于新元素或栈为空,然后将新元素入栈。
核心代码框架
#include <vector>
#include <stack>
using namespace std;vector<int> nextGreaterElement(vector<int>& nums) {int n = nums.size();vector<int> res(n, -1); // 默认值为-1,表示没有找到stack<int> stk; // 用于存储元素索引的单调栈for (int i = 0; i < n; i++) {// 维护栈的单调递减性while (!stk.empty() && nums[stk.top()] < nums[i]) {int idx = stk.top(); // 栈顶元素索引stk.pop();res[idx] = nums[i]; // 找到了下一个更大的元素}stk.push(i); // 入栈当前元素索引}return res;
}739. 每日温度

class Solution {
public:vector<int> dailyTemperatures(vector<int>& temperatures) {int n = temperatures.size();vector<int> res(n,0);stack<int>stk;for(int i = 0;i<n;i++){// 递增while(!stk.empty() && temperatures[stk.top()]<temperatures[i]){int index = stk.top(); // 栈顶元素stk.pop();res[index] = i-index;//res[index] = temperatures[i];}stk.push(i);}for(int i = 0;i<n;i++){cout<<res[i]<<endl;}return res;}
};
496.下一个更大元素 I

思路:暴力法
直接足步循环
先找到和 nums1 对应的 nums2 数,找到后,在循环找更大的,找到就退出
class Solution {
public:vector<int> nextGreaterElement(vector<int>& nums1, vector<int>& nums2) {int n = nums1.size();int m = nums2.size();vector<int> res (n,-1); // -1代表没找到stack<int>stk;for(int i = 0;i<n;i++){int j = 0;while(nums1[i] != nums2[j]){j++;}for(int k = j+1; k<m;k++){if(nums2[k]>nums1[i]){res[i] = nums2[k];break;}}}return res;}
};
思路二:单调栈
我们可以先对 nums2 进行单调栈,找到他每个元素的的下一个更大的数
再根据 nums1 创建数组
class Solution {
public:vector<int> nextGreaterElement(vector<int>& nums1, vector<int>& nums2) {int n = nums1.size();int m = nums2.size();unordered_map<int, int> nxetnum;vector<int> res (n,-1); // -1代表没找到stack<int>stk;// 遍历 nums2for(int num : nums2){while(!stk.empty()&& stk.top()<num){nxetnum[stk.top()] = num;stk.pop();}stk.push(num);}// 如果没有更大元素,则对应结果为 -1;while(!stk.empty()){nxetnum[stk.top()] = -1;stk.pop();}// 从nums1 中查找对应的;for(int i = 0;i<n;i++){res[i] = nxetnum[nums1[i]];}return res;}
};
503.下一个更大元素II

思路:
因为可以循环,直接将数组进行拼接,这样就破解循环问题了,就如同前面的每日温度问题了
class Solution {
public:vector<int> nextGreaterElements(vector<int>& nums) {int n = nums.size();vector<int>realnums;// 暴力拼接for(int i = 0; i<2;i++){for(int num:nums){realnums.push_back(num);}}vector<int> res(2*n,-1);stack<int>stk;for(int i = 0;i<realnums.size();i++){while(!stk.empty() && realnums[stk.top()]<realnums[i]){int index = stk.top();stk.pop();res[index] = realnums[i];}stk.push(i);}vector<int>resnum;resnum.insert(resnum.end(),res.begin(),res.begin()+n);return resnum;}
};
代码优化一下:
class Solution {
public:vector<int> nextGreaterElements(vector<int>& nums) {int n = nums.size();vector<int>realnums(n,-1);stack<int>stk;for(int i = 0 ;i<2*n;i++){int num = nums[i % n];while(!stk.empty() && nums[stk.top()] <num){int index = stk.top();stk.pop();realnums[index] = num;}if(i<n){stk.push(i);}}return realnums;}
};
相关文章:

单调栈问题
原理 单调栈的核心原理是:在栈内保持元素的单调性(递增或递减) 单调递增栈: 用于处理“下一个更小的元素”问题。当新元素比栈顶元素小或等于时,直接入栈;否则,一直从栈顶弹出元素,…...

Hexo博客重新部署与Git配置
由于电脑重装了一次,发现之前Hexo与NexT主题版本过于落后,重新部署了下。 1 Node.js与git安装 这一块安装就不赘述了。去两个官网找安装文件安装即可。 node.js git 打开git以后配置的几个关键命令行。 git config --global user.name "你的gi…...

KUKA机器人专业名词解释
1、CCU Cabinet Control Unit (控制柜控制单元) 2、CIB Cabinet Interface Board (控制柜接口板) 3、HMI Human Machine Interface (人机界面);KUKA.HMI 是 KUKA 操作界面。 4、KCB …...
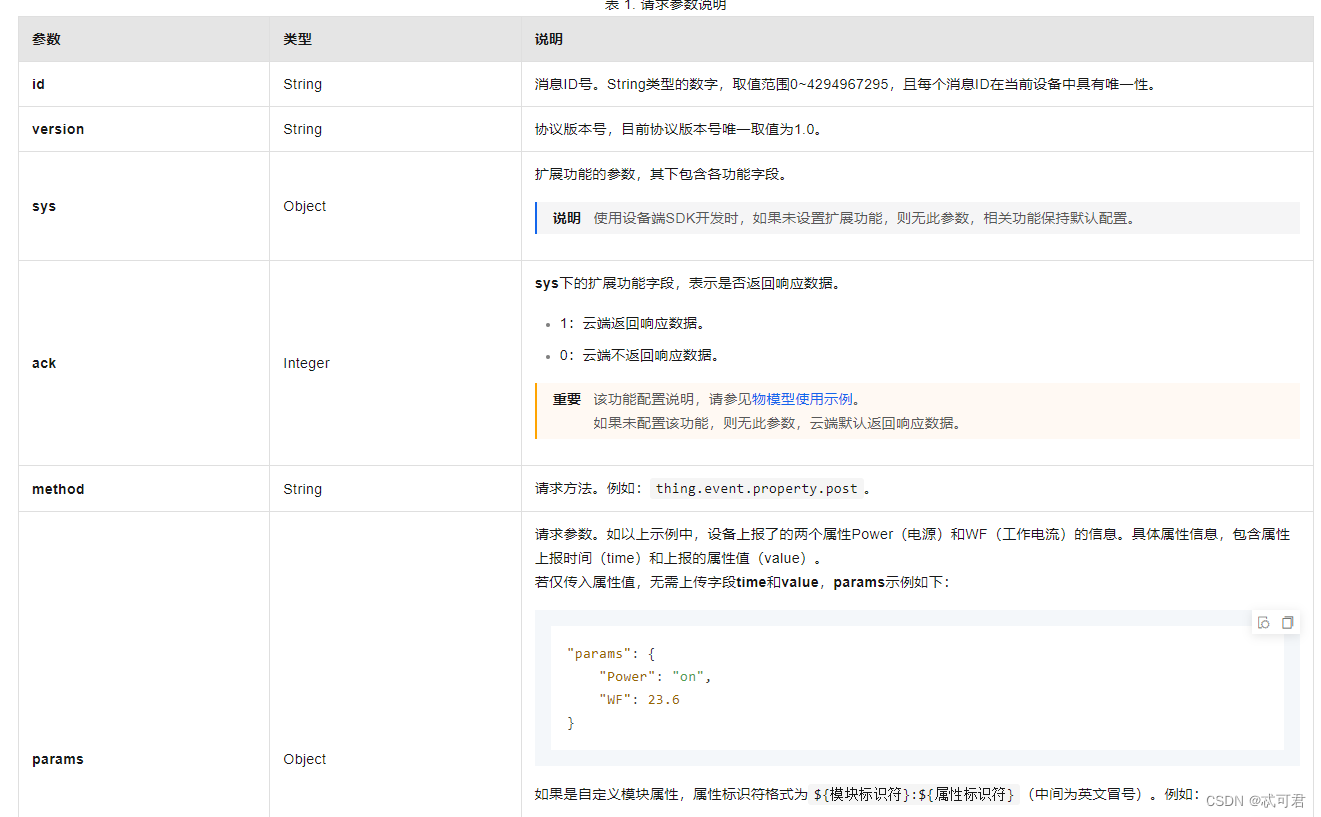
阿里云 物联网平台 MQTT连接、数据传输
阿里云 物联网平台 MQTT连接、数据传输 1、设备连接阿里云 2、多设备之前的通信、数据流转 3、设备数据来源的读取。 基于C# winform 开发上位机,读取设备、仪器、MES或者电子元器件的数据,MQTT传输至阿里云平台,可视化界面构建界面&#…...
栈和队列OJ练习题及解答
前言 上一篇博客已经讲到了栈和队列的数据结构,概括一下:栈后进先出(Last In First Out)、队列先进先出(First In First Out)。那么,接下来就来讲讲,关于栈和队列的相关练习题&#…...

渗透测试-信息收集
网络安全信息收集是网络安全领域中至关重要的一环,它涉及到对目标系统、网络或应用进行全面而细致的信息搜集和分析。这一过程不仅有助于理解目标网络的结构、配置和潜在的安全风险,还能为后续的渗透测试、风险评估和安全加固提供有力的支持。 在网络安…...

电力乙级资质延伸换证:企业转型的契机
电力乙级资质延伸换证不仅是企业合规运营的必要步骤,同时也为企业转型提供了重要的契机。在这个过程中,企业可以重新审视自身的业务模式、管理体系、技术能力等方面,寻找新的增长点和发展方向。 首先,电力乙级资质延伸换证要求企业…...

基于Redis实现分布式锁——Java版本
基于Redis实现分布式锁——Java版本 版本一版本二版本三Redisson 定义分布式锁接口如下: public interface ILock {boolean tryLock(long timeoutSec);void unlock(); }版本一 设定业务超时时间,到期自动解锁。缺点是超时时间不好估计,需要…...

Qt自定义控件--提升为
为什么要自定义控件 1,有复合小控件需要组合为一个整体控件时; 2,一个复合控件需要重复使用时; 实现 自定义控件文件 新增三个文件 关联不同组的控件 关联之前的准备工作 1,在主控件选择和子控件所有控件所在控件…...

Lua 基础 01 入门
Lua 基础相关知识 第一期 注释 -- 单行注释--[[多行注释 --]]-- 多加一个横杠符号就能重新启用注释内的代码 ---[[print("Lua") --]]数据类型 Lua 是动态类型语言,变量不需要类型定义,只需要为变量赋值。 Lua 有 8 种基本类型:…...
远程连接阿里云ECS
说明:ECS(阿里云服务器)可选择的系统镜像如下: 本文介绍基于Windows系统,对CentOS、Ubuntu、Windows这三个操作系统的连接方式,以及连接工具Windterm的使用。 CentOS & Windterm CentOS是我使用时间最…...
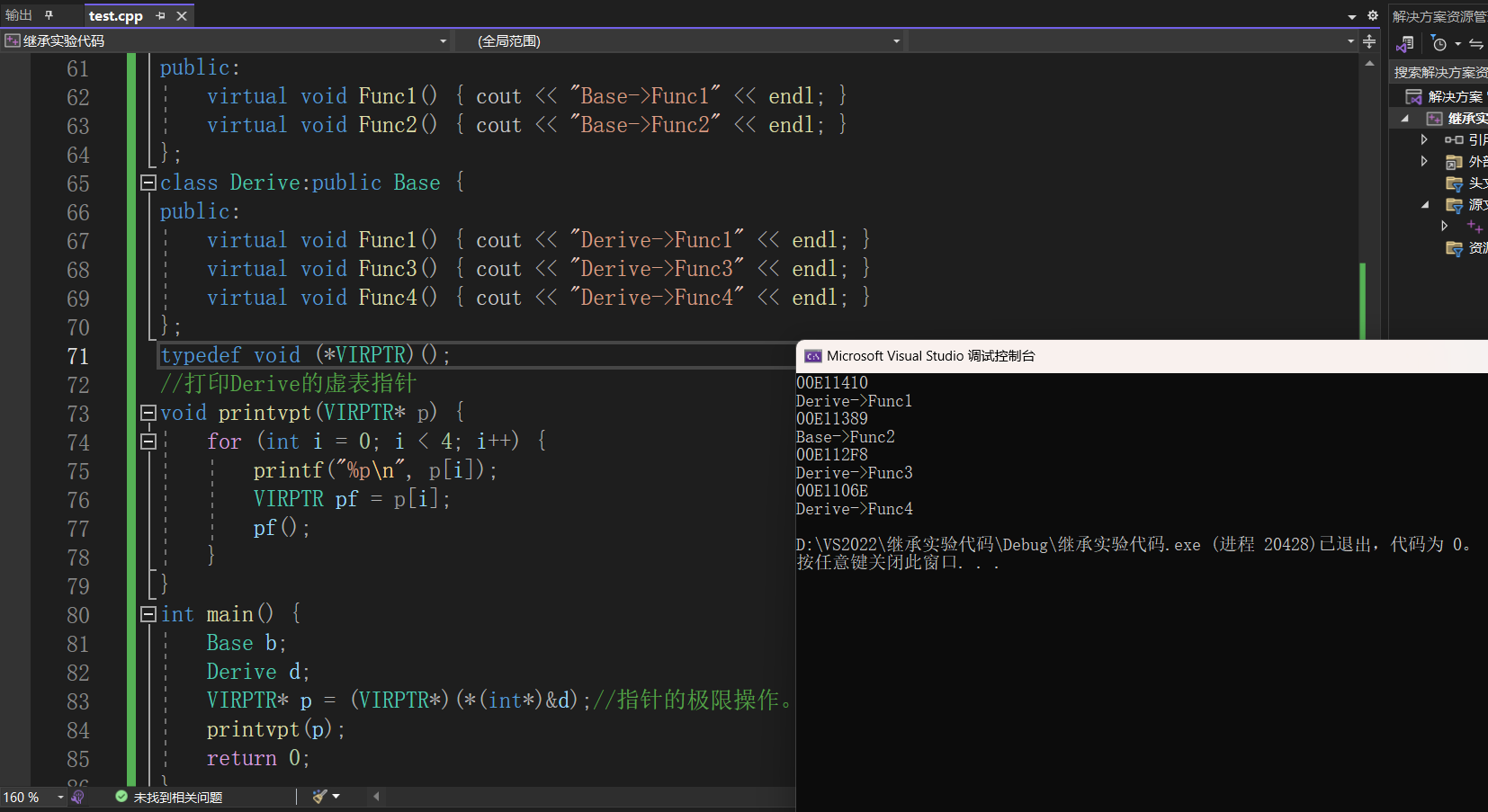
【C++】多态(上)超详细
封装,继承,多态不只是C的三大特性,而是面向对象编程的三大特性。 什么是多态: 不同的对象做同一件事情,结果会出现多种形态。 1.满足多态的几个条件 1.父子类完成虚函数重写(需要满足三同:函…...

【Git】 Git分支操作指南
隐形的纪念躲在心里面 也许吧 也许不会再见 阴天或晴天 一天又一年 风它在对我说莫忘这一切 🎵 蔡淳佳《隐形纪念》 Git是一种非常强大的分布式版本控制系统,允许用户在开发过程中创建不同的分支(branch)来分…...

智慧文旅赋能旅游服务升级:以科技创新驱动行业变革,打造智慧化、个性化、高效化的旅游新体验,满足游客日益增长的多元化需求
目录 一、引言 二、智慧文旅的概念与内涵 三、智慧文旅在旅游服务升级中的应用 1、智慧旅游服务平台建设 2、智慧景区管理 3、智慧旅游营销 四、智慧文旅推动旅游行业变革的案例分析 案例一:某智慧旅游城市建设项目 案例二:某景区智慧化改造项目…...

AtCoder Beginner Contest 310 E题 NAND repeatedly
E题:NAND repeatedly 标签:动态规划题意:给定一个长度为 n n n的 01 01 01字符串 A i A_i Ai,给定规则: 0 ⊼ 0 1 , 0 ⊼ 1 1 , 1 ⊼ 0 1 , 1 ⊼ 1 0 0⊼01,0⊼11,1⊼01,1⊼10 0⊼01,0⊼11,1⊼01,1⊼10。 求 ∑…...

一款简易的免费抽奖软件
一、介绍 这款抽奖软件设计简洁,操作便捷。用户可以轻松将参与名单通过EXCEL文件导入至程序中,并可根据需要设定各类奖品和对应的中奖人数。在选定了奖品后,用户只需点击“开始”按钮,随后再按下“暂停”按钮,软件便会…...

Kubernetes 监控管理
目录 1. Metrics Server2. Prometheus & Grafana3. cAdvisor4. 日志收集5. 告警与通知6. 最佳实践 Kubernetes 监控管理是确保集群稳定运行和应用服务质量的关键环节。它涉及收集、聚合、分析集群及其上运行的应用程序的各种指标和日志数据。 1. Metrics Server 作用&…...

哈希表第6/9题--四数相加II
题目描述: 给你四个整数数组 nums1、nums2、nums3 和 nums4 ,数组长度都是 n ,请你计算有多少个元组 (i, j, k, l) 能满足: 0 < i, j, k, l < nnums1[i] nums2[j] nums3[k] nums4[l] 0 示例 1: 输入&…...

使用JavaScript将富文本HTML转换为纯文本
在Web开发中,我们经常需要处理HTML内容,但有时为了特定的目的,比如文本处理、搜索或显示在非HTML环境中,我们可能希望将富文本HTML转换为纯文本。这里,我们将探讨如何使用JavaScript来实现这一功能。 为什么要将HTML转…...

2024-05-13 问AI: 介绍一下 google wavenet 声码器
文心一言 Google的WaveNet声码器是一个深度学习模型,用于生成高质量的音频信号,特别是人类语音。与传统的声码器相比,WaveNet可以生成更加自然和流畅的音频,因为它直接模拟了原始音频信号的波形生成过程。 WaveNet的核心思想是使…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...
