04 贝尔曼最优公式
贝尔曼最优公式
- 前言
- 1、Motivating examples
- 2、Definition of optimal policy
- 3、Bellman optimality equation(BOE):Introduction
- 4、 BOE:Maximization on the right-hand side
- 5、BOE:Rewrite as v = f(v)
- 6、Contraction mapping theorem
- 7、BOE:Solution
- 8、BOE:Optimality
- 9、Analyzing optimal policies
前言
本文来自西湖大学赵世钰老师的B站视频。
本节课介绍最优策略和贝尔曼最优公式。贝尔曼最优公式是贝尔曼公式的一个特殊情况,本次学习有两个重要概念和一个工具。
(1) 两个概念:optimal state value 和optimal policy.
(2) 一个工具:bellman optimality equation(BOE).
强化学习的目标就是寻找最优策略,因此本文主要讲最优策略。本文大纲如下:

1、Motivating examples

这是上节课介绍的贝尔曼方程,有了贝尔曼方程,我们就可以求解state value,有了state value,我们就可以进一步求解action value。下图是求解action value的流程,以状态s1出发为例:

以上是对前几次课的复习,由此我们可以提出一个问题,就是当前这个策略如果是不好的,我们应该怎么去提升它?这个就依赖于action value。当前的策略可以写成以下形式:
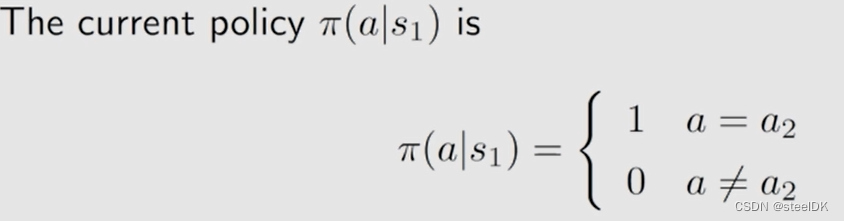

由上可知,我们已经知道a3是最好的,如果选择a3是这个新的策略,我们就获得了new policy。新的策略就是对应action value 最大。
我们首先对每一个状态都选择action value最大的 action,选择完了一次,然后再来一次迭代得到了一个新的策略,就这样不断迭代,最后那个策略就会趋向于一个最优的策略。
2、Definition of optimal policy

3、Bellman optimality equation(BOE):Introduction

贝尔曼最优公式就是在贝尔曼公式的前面加一个max,这个max就涉及到一个优化问题,就是要先解决优化问题,求解出一个策略π,带入到贝尔曼公式中。

上面是矩阵形式。

4、 BOE:Maximization on the right-hand side
下面是BOE的两种表示形式,实际上我们是得到一个式子,但有两个未知量,如何求解呢?
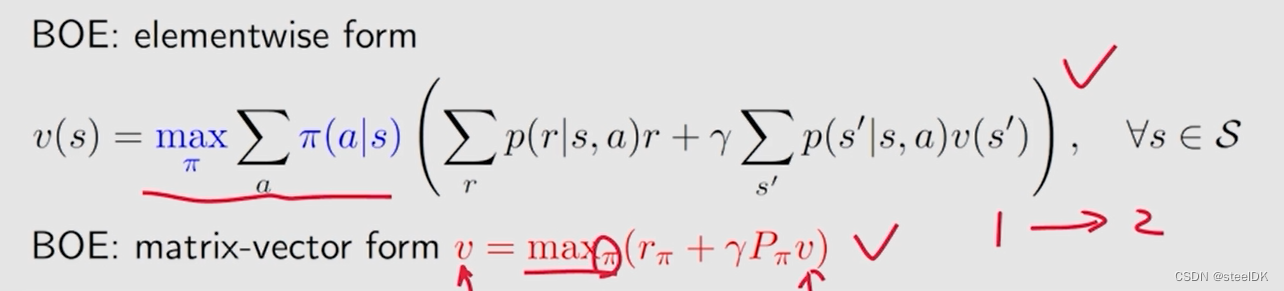
下面是一个小例子:

这个小例子的求解思路就可以放到贝尔曼最优公式求解中。
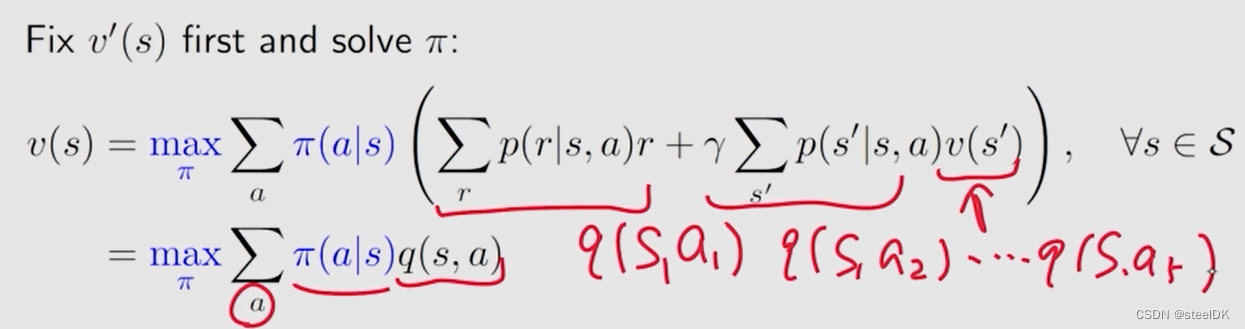
我们先给定公式右边的v(s’)一个初值,这样q(s,a)就是确定的了,此时我们需要把π(a|s)确定下来。我们知道对于网格问题有5个action,则有5个q(s,a),我们怎样求解π(a|s)?再看一个例子,假设有3个q值:
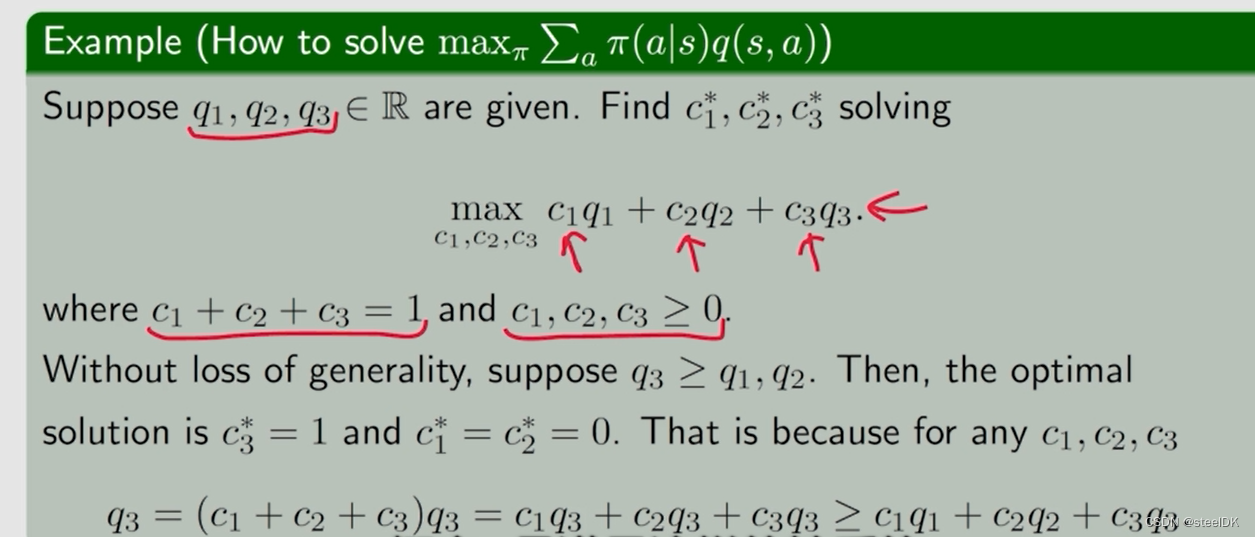

至此,我们解决了π(a|s)如何求解的问题。
5、BOE:Rewrite as v = f(v)
本文第4小节,我们知道了如何选择π(a|s),此时贝尔曼最优公式的求解问题就变的比较简单了,我们就可以给等式右边一个初值,用矩阵迭代求解了。

6、Contraction mapping theorem
下面介绍一些概念:



以上实际上是迭代法求解矩阵收敛性的公式证明。

7、BOE:Solution

8、BOE:Optimality



9、Analyzing optimal policies
利用贝尔曼最优公式我们求解最优的策略,求解最优的state value。下面我们就用这个工具分析一些最优的策略。

已知红色的量,把黑色的量求解出来。

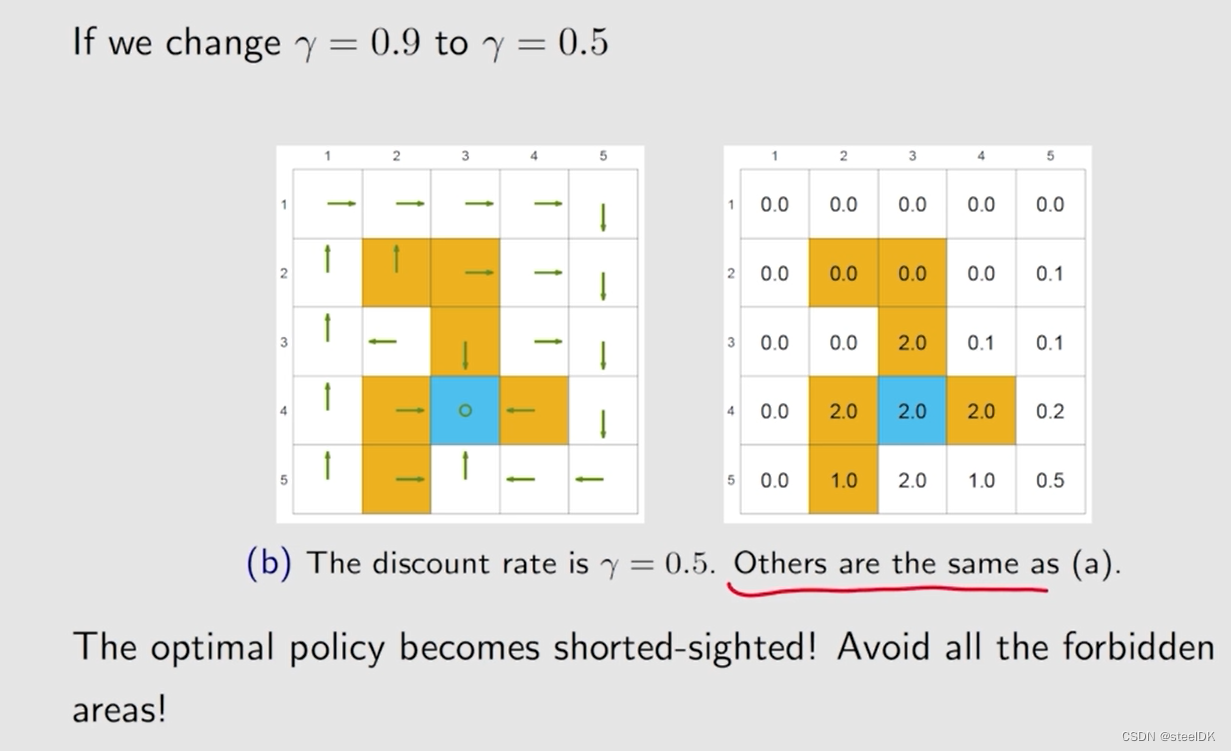
γ比较大的时候,策略会考虑的更长远。相反,γ如果等于0,策略会更加短视。

当我们把forbidden arera的惩罚值设置的比较大时,策略会选择绕过forbidden area。

策略选择的重点不在于奖励值设置的绝对大小,而在于相对大小。

下面再看一个例子:

很多人可能会觉得,我每走一步,应该给一个惩罚,即r=-1,实际当中这个r=-1就代表一种能量的消耗,这样的话智能体就不会绕远路,它就会尽可能地走最短的路径到目标区域,如果没有r=-1的话,好像就会绕远路,是这个样子吗?通过上图示例我们可以发现并不是这样子的,因为除了r来约束它不要绕远路之外,还有γ,因为它越绕远路就意味着我得到到达目标的奖励越晚,那么对应γ的次方就会越大,那么打折就会越厉害,所以它自然就会找一个最短的路径过去。
最后总结如下:

相关文章:

04 贝尔曼最优公式
贝尔曼最优公式 前言1、Motivating examples2、Definition of optimal policy3、Bellman optimality equation(BOE):Introduction4、 BOE:Maximization on the right-hand side5、BOE:Rewrite as v f(v)6、Contraction mapping theorem7、BO…...

印象笔记使用技巧
印象笔记(Evernote)是一款广泛使用的笔记应用,它帮助用户整理个人信息、文件和备忘录。以下是一些提高在印象笔记中效率的使用技巧: ### 1. 使用标签和笔记本组织笔记 - **建立笔记本**:为不同的项目或类别创建笔记本…...
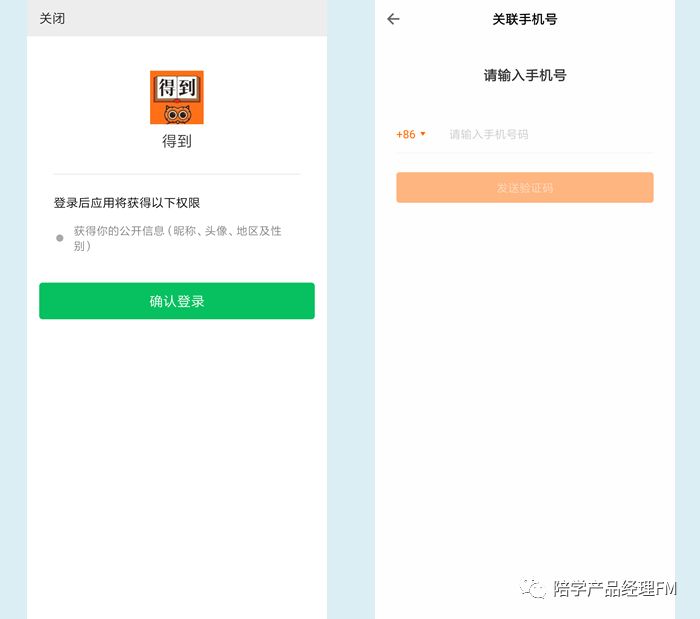
产品设计中的“注册”说明
在使用网站或应用的时候必不可少的就是账号系统,账号系统有些人可能觉得简单,无非就是账号密码。真的是这样吗? 一个完整的账号系统通常大家会分成四部分: 1.注册(手机号、邮箱、用户名/密码限制/验证码)…...
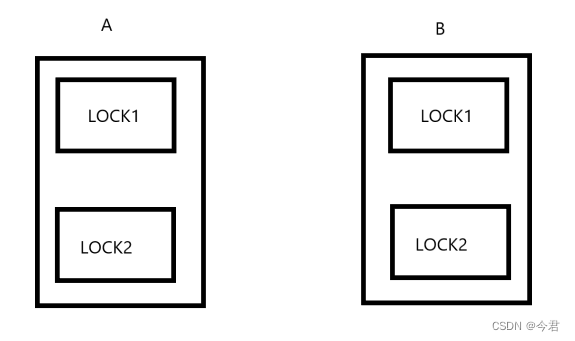
【linux学习】多线程(1)
文章目录 线程的概念线程与进程 线程的用法线程的创建多线程 线程的等待线程锁死锁 线程的概念 在Linux中,线程(Thread)是程序执行流的最小单位,是进程中的一个实体,负责在程序中执行代码。线程本身不拥有系统资源&…...

Leetcode 3149. Find the Minimum Cost Array Permutation
Leetcode 3149. Find the Minimum Cost Array Permutation 1. 解题思路2. 代码实现 题目链接:3149. Find the Minimum Cost Array Permutation 1. 解题思路 这一题的话就是一个动态规划的问题,不过他这个错位着实是把题目变得复杂了不少,唉…...

Python | 为列表中的元素分配唯一值
我们可以给列表中的所有数字分配一个唯一的值,重复时它会保留给它的值。这是一个非常常见的问题,在Web开发中,处理物品id时会遇到。让我们讨论一下解决这个问题的一些方法。 1. 使用enumerate() 列表解析 # initializing list test_list …...
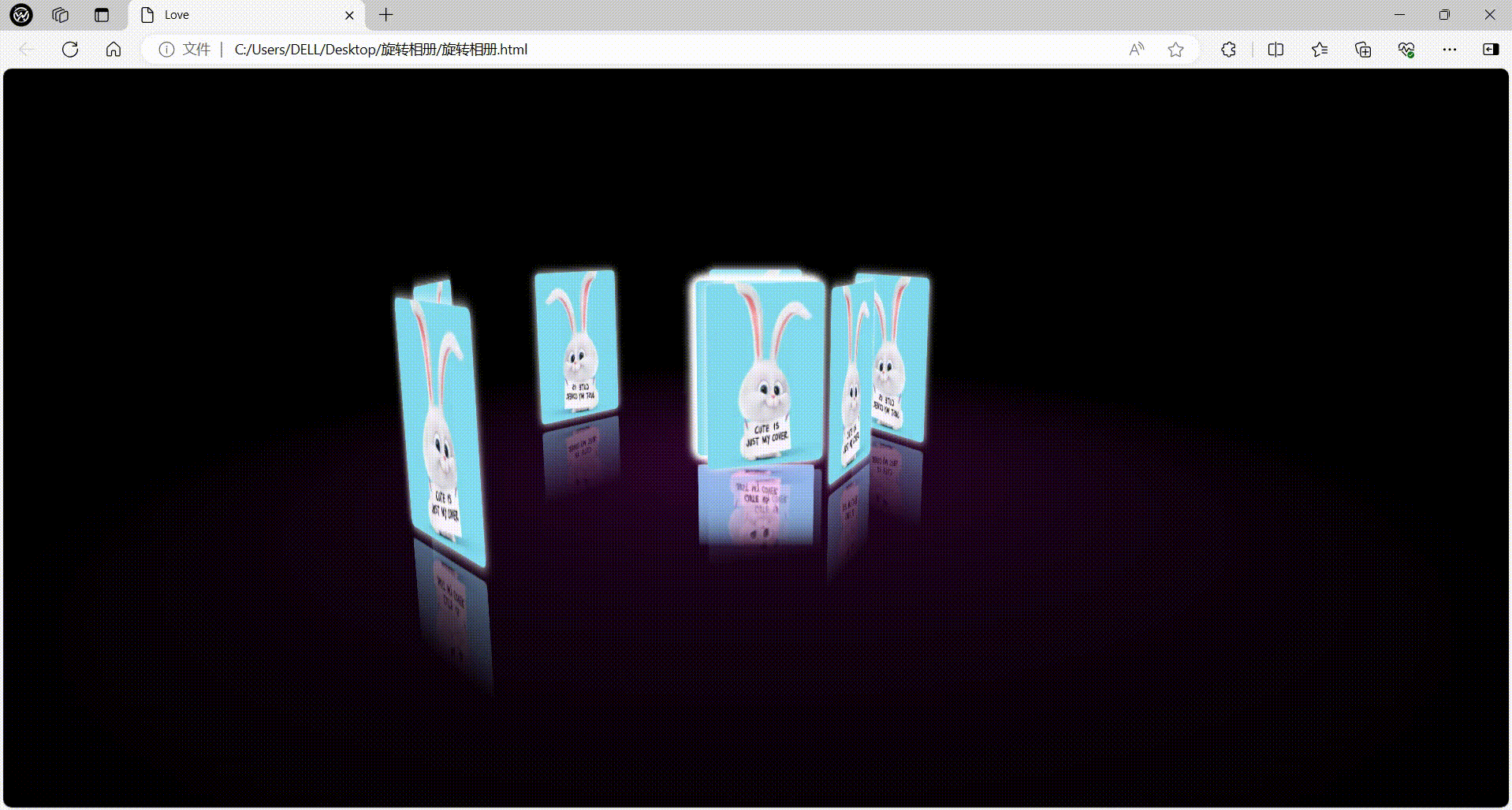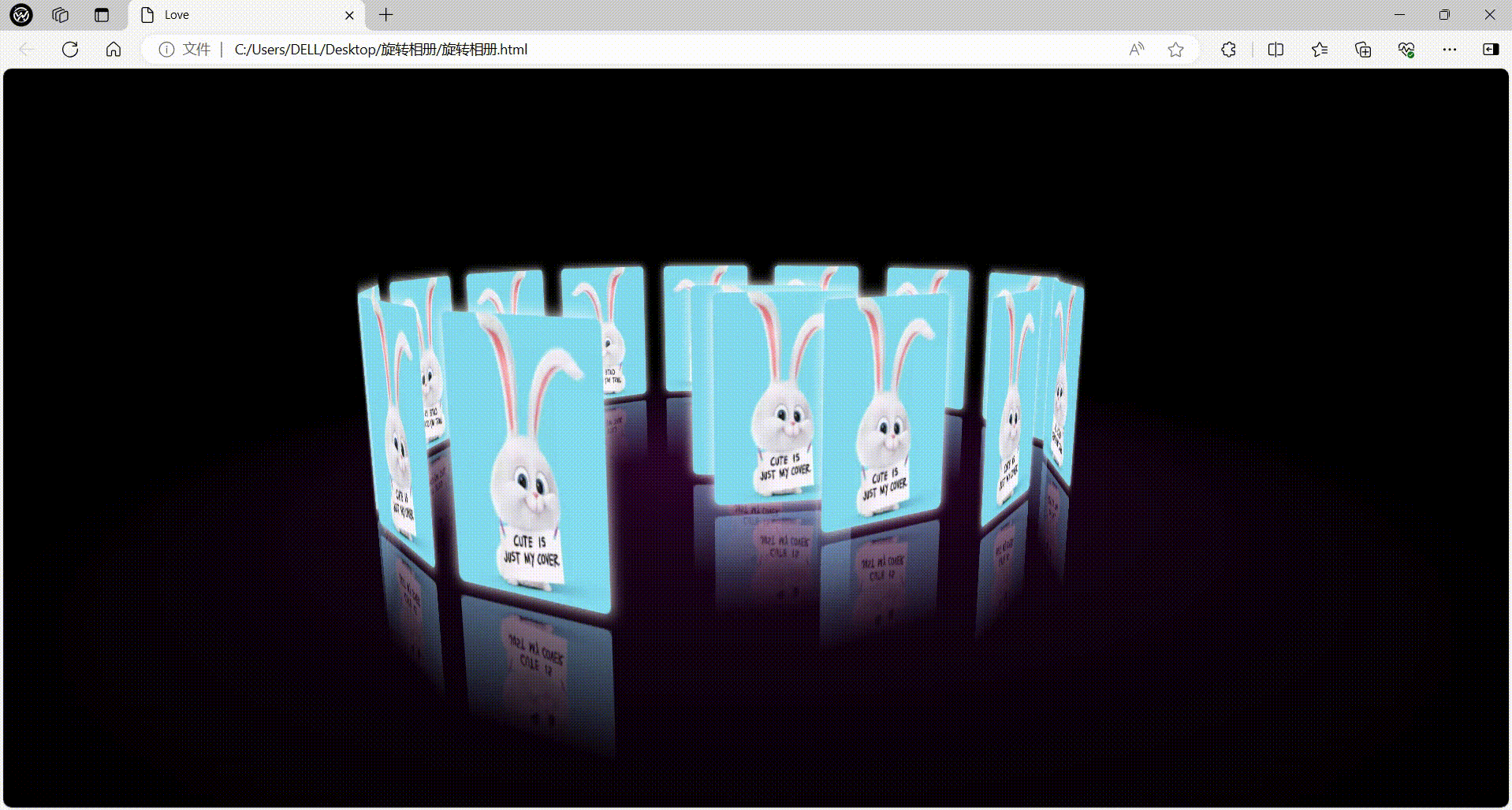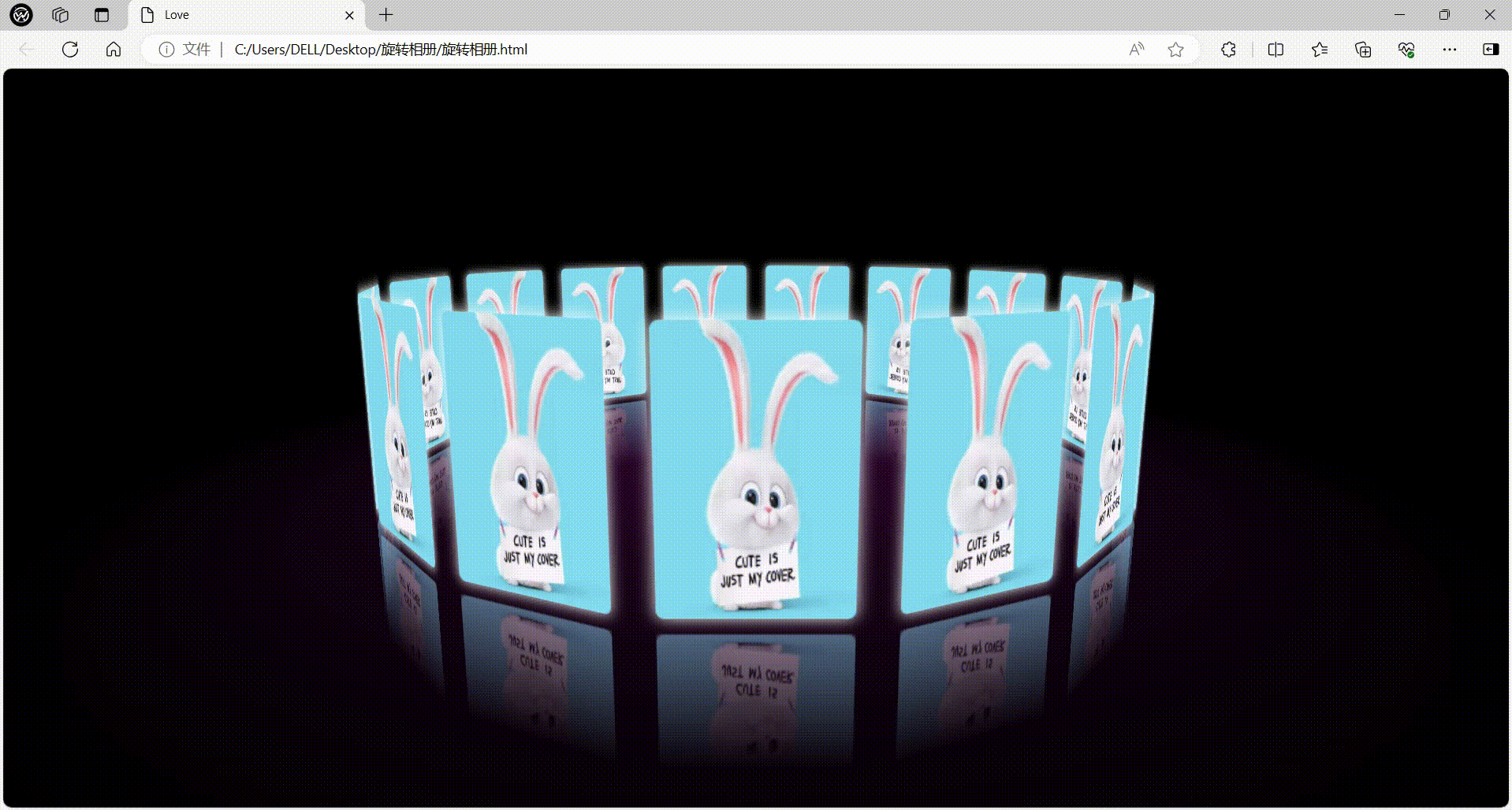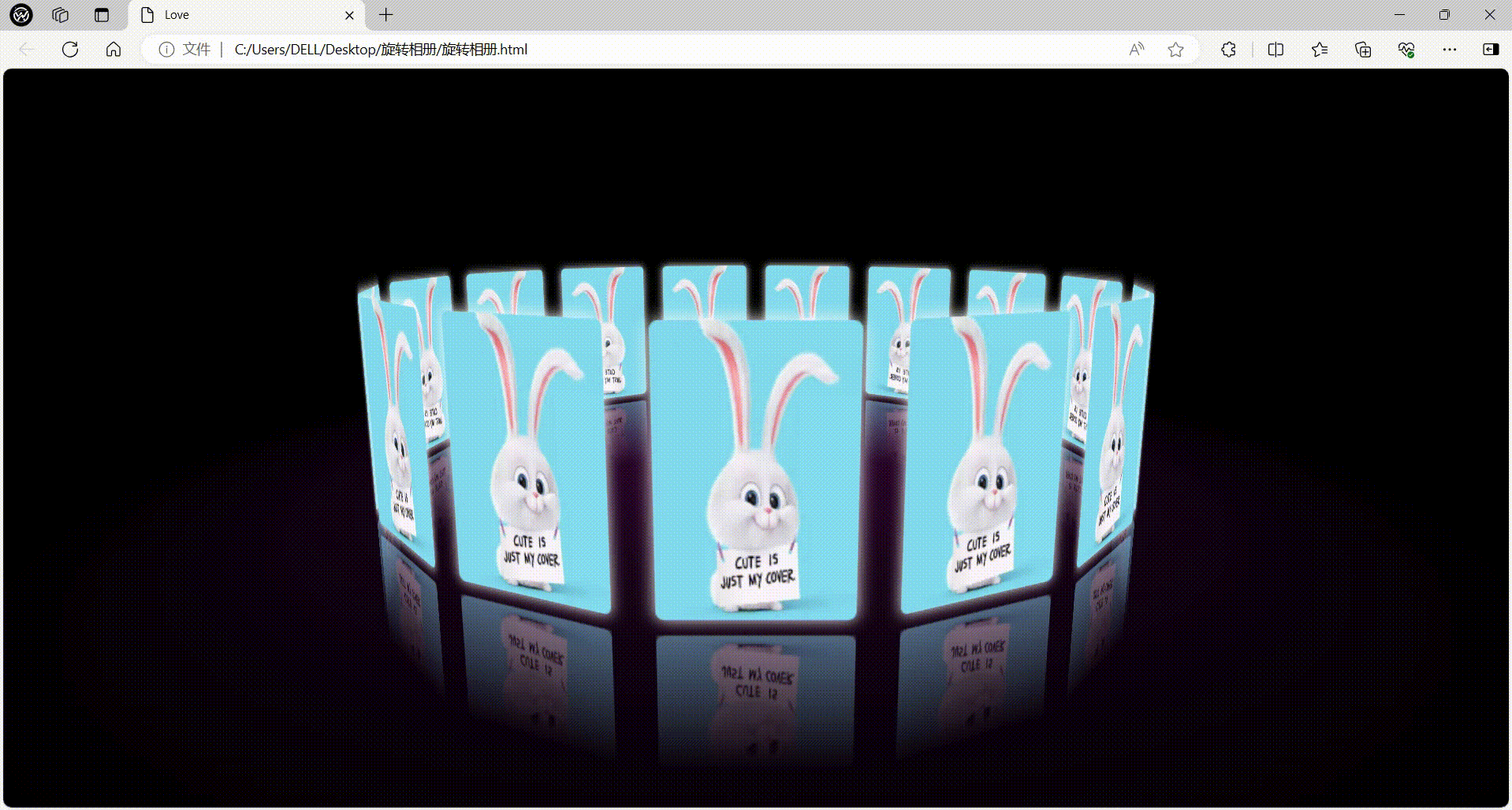
HTML炫酷的相册
目录 写在前面 HTML简介 完整代码 代码分析 系列推荐 写在最后 写在前面 本期小编给大家带来一个炫酷的旋转相册,快来解锁属于你的独家记忆吧! HTML简介 HTML(全称为超文本标记语言)是一种用于创建网页结构和内容的标记语…...
C++笔试强训day20
目录 1.经此一役小红所向无敌 2.连续子数组最大和 3.非对称之美 1.经此一役小红所向无敌 链接 简单模拟即可。 需要注意的是: 除完之后有无余数,若有,则还可以再挨一次打。 #include <iostream> using namespace std; #define in…...

【PHP【实战项目】系统性教学】——使用最精简的代码完成用户的登录与退出
👨💻个人主页:开发者-曼亿点 👨💻 hallo 欢迎 点赞👍 收藏⭐ 留言📝 加关注✅! 👨💻 本文由 曼亿点 原创 👨💻 收录于专栏:…...
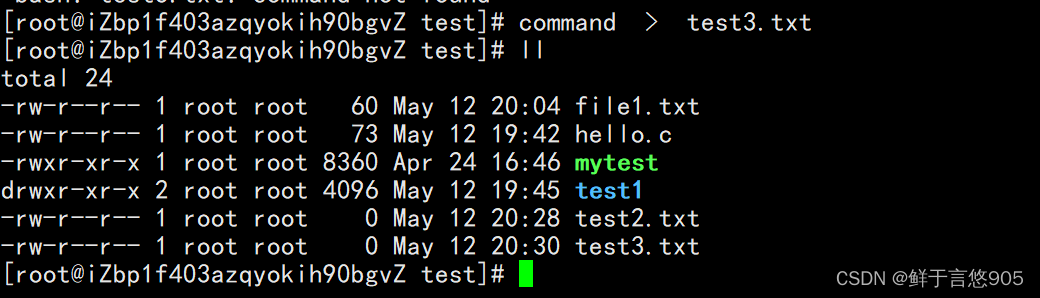
Linux下的常用基本指令
基本指令 前言一、ls 指令语法功能常用选项举例注意要点关于拼接关于 -a关于文件ls与/的联用ls与根目录ls与任意文件夹ls与常用选项与路径 ls -d与ls -ldls与ll 二、pwd命令语法功能常用选项注意要点window与Linux文件路径的区别家目录 三、cd 指令语法功能举例注意要点cd路径.…...

phpstorm环境配置与应用
在 PhpStorm 中配置 PHP 开发环境及进行一些常用的应用设置涉及以下几个主要步骤: ### 1. 安装和激活 PhpStorm - **下载安装**: 访问 JetBrains 官网下载最新版本的 PhpStorm 安装包,然后按照提示进行安装。 - **激活**: 启动 PhpStorm,你可…...

【Qt 学习笔记】Qt常用控件 | 布局管理器 | 水平布局Horizontal Layout
博客主页:Duck Bro 博客主页系列专栏:Qt 专栏关注博主,后期持续更新系列文章如果有错误感谢请大家批评指出,及时修改感谢大家点赞👍收藏⭐评论✍ Qt常用控件 | 布局管理器 | 水平布局Horizontal Layout 文章编号&…...
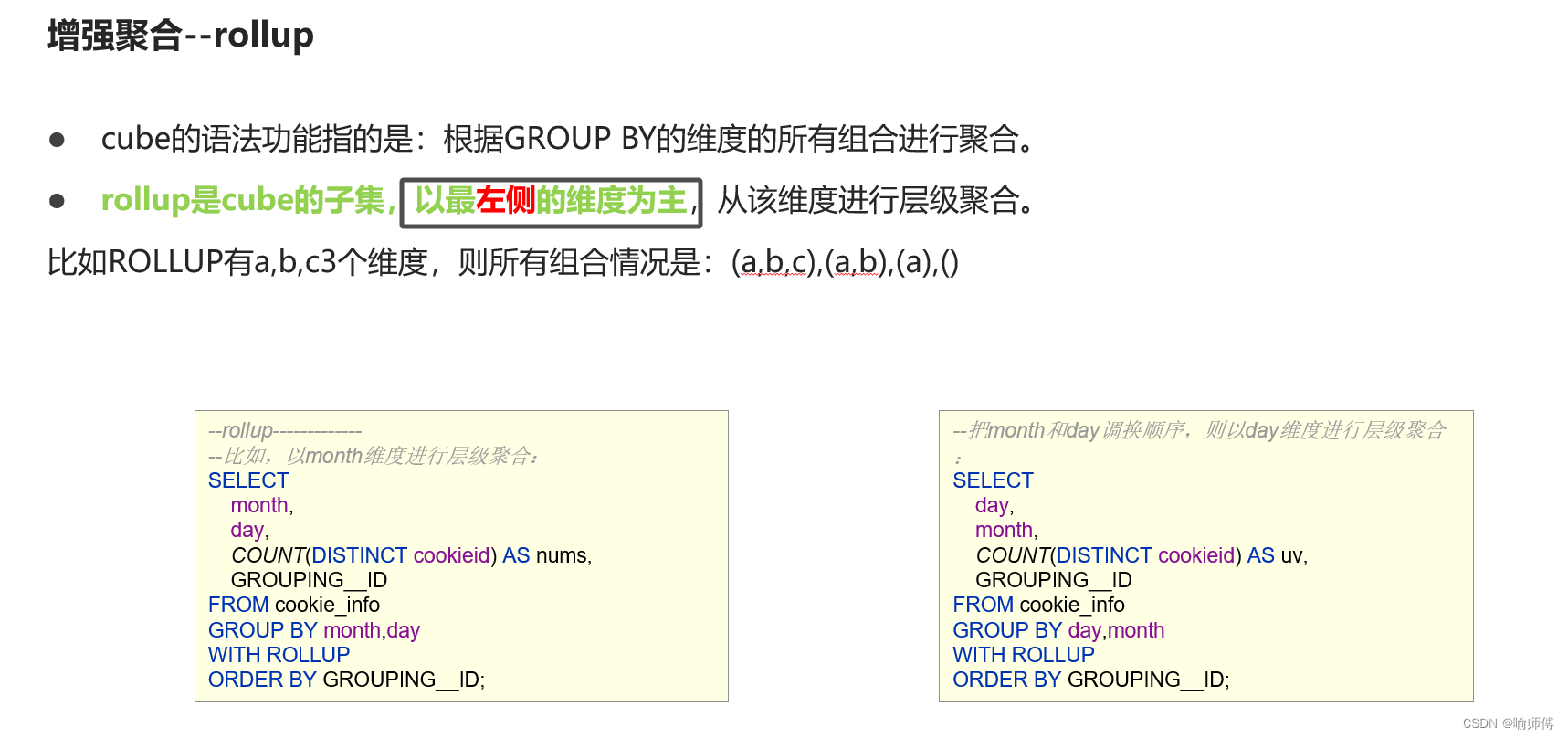
Hive Aggregation 聚合函数
Hive Aggregation 聚合函数 基础聚合 增强聚合...
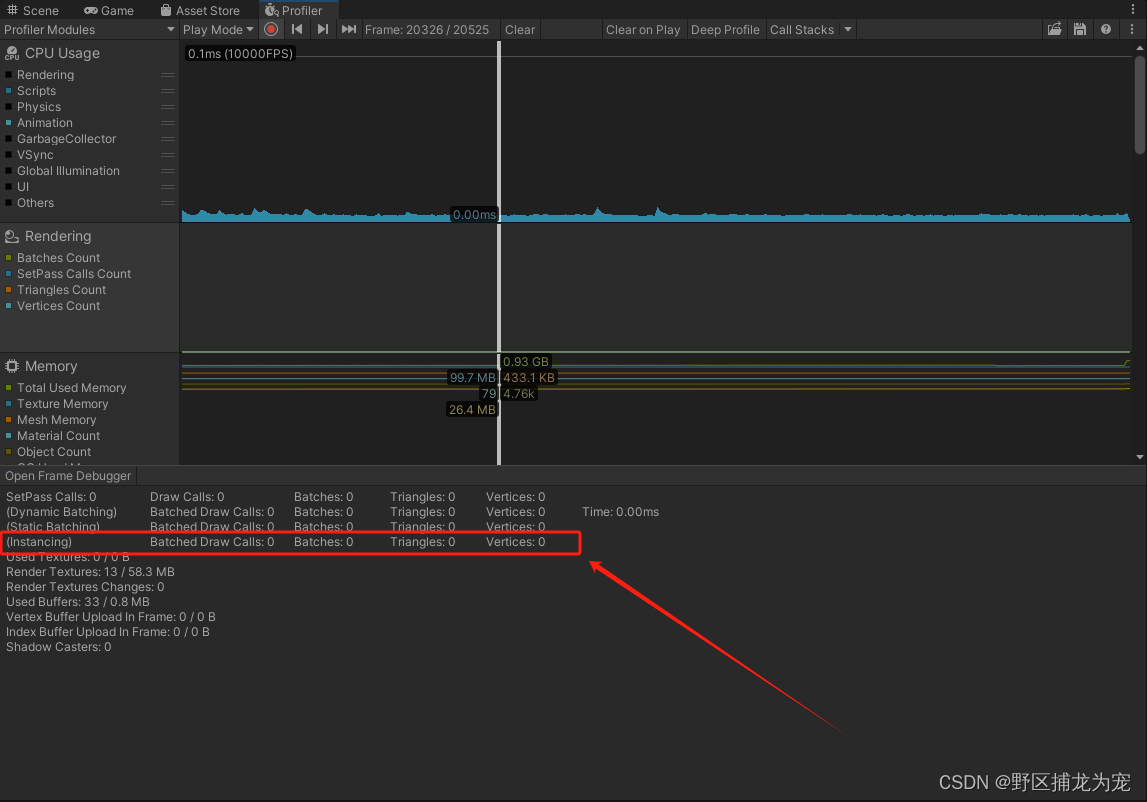
Unity 性能优化之GPU Instancing(五)
提示:仅供参考,有误之处,麻烦大佬指出,不胜感激! 文章目录 前言一、GPU Instancing使用方法二、使用GPU Instancing的条件三、GPU Instancing弊端四、注意五、检查是否成功总结 前言 GPU Instancing也是一种Draw call…...
LeetCode 138. 随机链表的复制
目录 1.原题链接: 2.结点拆分: 代码实现: 3.提交结果: 4.读书分享: 1.原题链接: 138. 随机链表的复制 2.结点拆分: ①.拷贝各个结点,连接在原结点后面; ②.处…...

【PC微信小程序点不动处理方法】
描述 在使用电脑小程序抓包的时候发现原来能点的小程序今天不能点了。就是原来有个输入车牌号的输入框点击会出现车牌号键盘,现在不行了,经过卸载安装发现不是微信的问题,是WeChatAppEx.exe 的bug。早期使用的是不带ex的都没有问题升级以后&…...

量化交易:日内网格交易策略.md
哈喽,大家好,我是木头左! 本文将详细介绍日内网格交易策略的原理,并结合Python代码示例,展示如何在掘金平台上实现这一策略。 策略原理 日内网格交易策略的核心思想是在一天的交易时间内,通过设置多个买卖…...
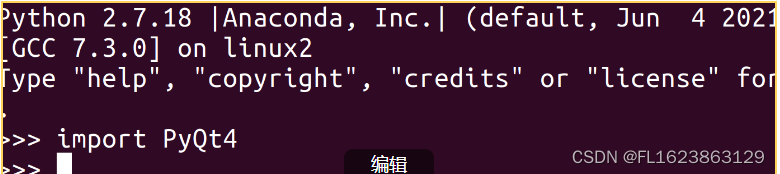
Ubuntu 20.04在Anaconda虚拟环境中配置PyQt4
一、创建一个虚拟环境 1 创建一个python2.7的虚拟环境: conda create -n pyqt4 numpy matplotlib python2.72 在环境中安装几个需要的包: pip install Theano pip install python-opencv3.4.0.14 pip install qdarkstyle pip install dominate二、在主…...

charts3D地球--添加航线
要在地球视角下画出海运路线图 方案 添加 globl 地球创建geo地理坐标系创建canvas对象用于承载地图世界地图this.worldChart //初始化canvas节点let cav document.createElement("canvas");this.$echarts.registerMap("world", geoJson);this.worldCha…...

变色龙还是树懒:揭示大型语言模型在知识冲突中的行为
你是知识变色龙还是树懒?我今天在ICLR学到一个很有趣的术语,叫做证据顺序(order of evidence)。 大模型RAG处理知识冲突的探讨: 在检索增强生成(Retrieval-Augmented Generation, RAG)的过程中,技术团队会将检索到的前几名文档作为证据,并提示(prompt)给大型语言模型(Large La…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...

ubuntu系统文件误删(/lib/x86_64-linux-gnu/libc.so.6)修复方案 [成功解决]
报错信息:libc.so.6: cannot open shared object file: No such file or directory: #ls, ln, sudo...命令都不能用 error while loading shared libraries: libc.so.6: cannot open shared object file: No such file or directory重启后报错信息&…...

C++实现分布式网络通信框架RPC(2)——rpc发布端
有了上篇文章的项目的基本知识的了解,现在我们就开始构建项目。 目录 一、构建工程目录 二、本地服务发布成RPC服务 2.1理解RPC发布 2.2实现 三、Mprpc框架的基础类设计 3.1框架的初始化类 MprpcApplication 代码实现 3.2读取配置文件类 MprpcConfig 代码实现…...
