【数据结构】堆(Heap)
文章目录
- 一、堆的概念及结构
- 二、堆的实现
- 1.向上调整算法
- 2.向下调整算法
- 3.堆的创建
- 4.堆的插入
- 5.堆的删除
- 6.堆的其他操作
- 三、堆的应用
- 1.堆排序
- 2.Top-K问题
一、堆的概念及结构
堆(Heap)是一种特殊的非线性结构。堆中的元素是按完全二叉树的顺序存储方式存储在数组 中。满足任意结点的值都大于等于左右子结点的值,叫做大堆,或者大根堆;反之,则是小堆,或者小根堆。
不熟悉二叉树的小伙伴可以先跳转→二叉树详解←学习。
堆分为小根堆和大根堆。
小根堆:所有父结点都小于等于左右孩子结点。
大根堆:所有父结点都大于等于左右孩子结点。
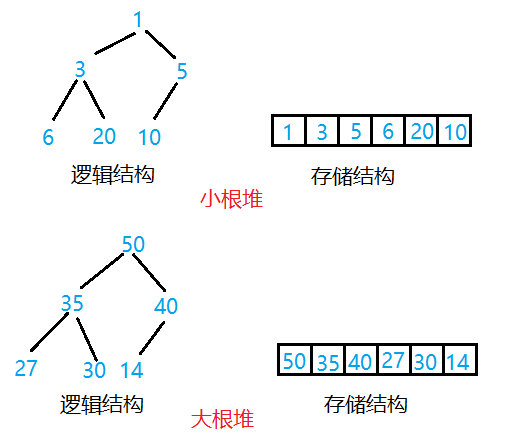
堆的性质:
1.堆是一棵完全二叉树。
2.堆中某个节点的值总是不大于或不小于其父节点的值。
3.如果一个堆为大(小)根堆,则它的左右子树也都是大(小)根堆。
4.小堆的存储结构不是升序,大堆的存储结构也不是降序。
5.堆中任意结点下标为 i,则它的左孩子结点下标为2i+1,右孩子结点下标为2i+2,父结点下标为(i-1)/2。
二、堆的实现
堆的两个重要算法:向上调整和向下调整。
1.向上调整算法
向上调整一般在堆中插入元素时使用。
具体实现(小根堆示例):
1.给定一个数组和一个结点下标,该结点与其父结点的值进行比较。
2.如果该结点的值 ≥ 其父结点的值,已经是小堆了,则不再继续调整;
3.如果该结点的值 < 其父结点的值,需要将二者交换,然后将父结点当做孩子结点,继续向上对比和交换,直到调整到堆顶。
如果是小根堆,只需要改变判断符号>改为<即可。
//小根堆 向上调整
void AdjustUp(DataType* a, int child)
{int parent = (child - 1) / 2;//父结点下标while (a[child] < a[parent])//建大堆{Swap(&a[child], &a[parent]);child = parent;parent = (child - 1) / 2;}
}
//交换函数
void Swap(DataType* p1, DataType* p2)
{DataType tmp = *p1;*p1 = *p2;*p2 = tmp;
}
向上调整算法的比较次数最多不超过二叉树的高度,所以时间复杂度为O(logN)
2.向下调整算法
堆的向下调整算法比较常用,堆排序和堆的创建都会用到向下调整算法。
向下调整算法有一个前提:左右子树必须是一个堆,才能调整。
具体实现(小根堆示例):
1.从该结点开始,与其左右孩子结点中比较大(较小)的结点进行比较。
2.如果该结点的值 ≤ 其较小(较大)孩子结点的值,已经是小堆了,则不再继续调整;
3.如果该结点的值 > 其较小(较大)孩子结点的值,需要将二者交换,然后将较小的孩子结点当做父结点,继续向下对比和交换,直到调整到叶子结点。
//向下调整
void AdjustDown(DataType* a, int parent, int n)
{int child = 2 * parent + 1;while (child < n){//选出较小的孩子if (child + 1 < n && a[child + 1] < a[child])//右孩子不能越界访问,注意判断顺序不能反{child++;}if (a[parent] > a[child]){Swap(&a[parent], &a[child]);parent = child;child = 2 * parent + 1;}else{break;}}
}
同样,向下调整算法的比较次数最多也不会超过二叉树的高度,所以时间复杂度为O(logN)
3.堆的创建
给定一个数组,怎么创建成一个堆呢? 根结点的左右子树都不是堆,该怎么调整?
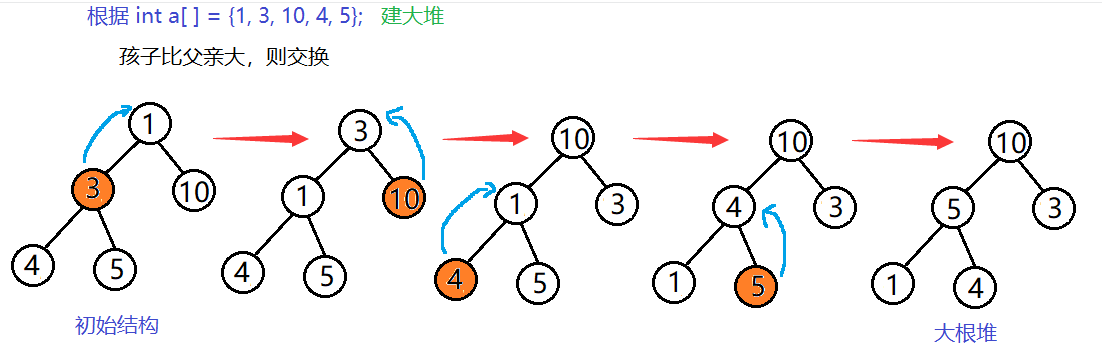
向上调整建堆:
从根结点开始调整
从根结点的左孩子结点开始(因为根结点本身可以看做一个堆),每个结点都向上调整,此时该结点前面的所有结点都已经构成了一个堆,直到调整到最后一个结点,就可以调整成堆。
// 向上调整建堆 效率O(N*logN)
for (int i = 1; i < n; i++)
{AdjustUp(a, i);
}
 向上调整建堆的时间复杂度是多少?
向上调整建堆的时间复杂度是多少?
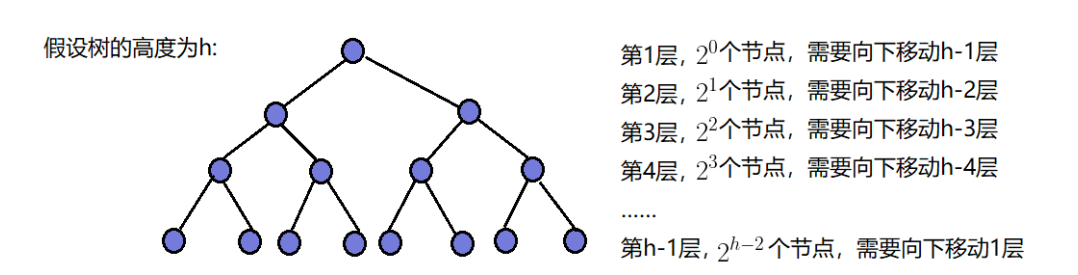
每个结点最多需要向上调整的次数与层数有关,若层数为k,则最多最多向上调整logk次。而随着层数越大,每层的结点数也越多。假设二叉树的高度为h,则向上调整为堆最多需要调整的次数为0×20+1×21+2×22+3×23+…+(h-1)×2h-1
= (h-2)×2h(错位相减,高中知识,具体过程略),又因为树的高度h=log(n+1),所以时间复杂度的量级为O(N*logN)。
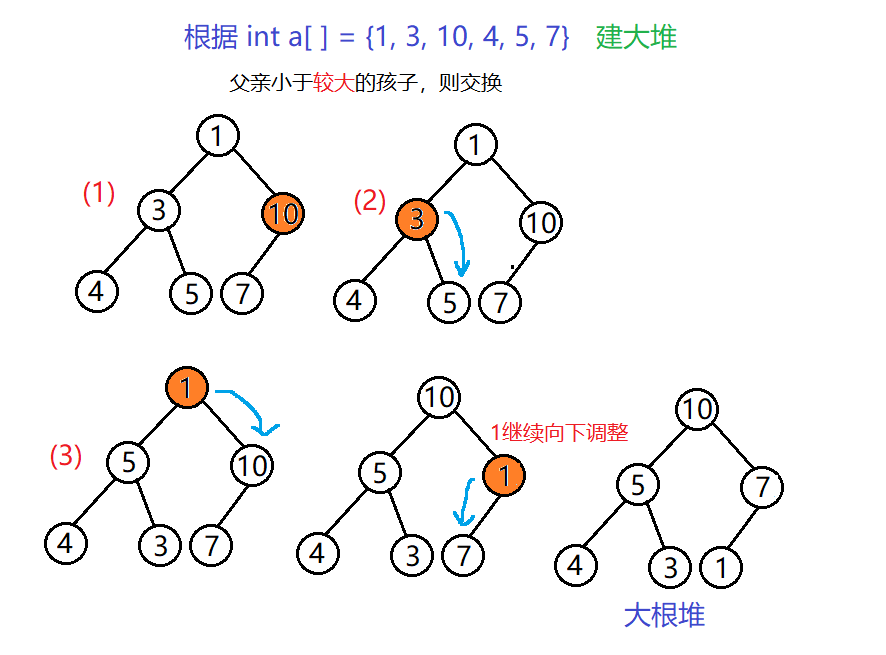
向下调整建堆:
从最后一个非叶子结点开始倒着调整
因为向下调整建堆需要满足左右子树都是堆的前提,所以我们可以从最后一个结点开始依次向下调整,因为最后一个结点本身可以看做是一个堆。但是因为叶子结点向下调整并不会发生变化,所以我们可以优化代码,从最后一个叶子结点的父结点也就是最后一个非叶子结点开始调整。
//向下调整建堆 效率O(N)
for (int i = (n - 1 - 1) / 2; i >= 0; i--)
{AdjustDown(a, i, n);
}
 向下调整建堆的时间复杂度是多少?
向下调整建堆的时间复杂度是多少?
因为向下调整建堆是从最后一个非叶子结点开始倒着调整的,随着层数的减小,每层的结点数也越少,但是结点向下调整的次数在增加,具体推导过程这里不过多介绍,最后的时间复杂度的量级是O(N)。
综上所述,向上调整建堆的时间复杂度为O(N*logN),向下调整建堆的时间复杂度为O(N),所以使用向下调整建堆的效率更高效。实际应用中,一般都使用向下调整算法建堆。
堆的定义、初始化、销毁
堆是以数组的方式存储的,所以堆的定义、初始化、销毁和顺序表一样。
#define INIT_SZ 10//初始空间大小
#define INC_SZ 4 //每次扩容的数量
typedef int HDataType;
typedef struct Heap
{HDataType* a;int size;int capacity;
}Heap;//初始化
void HeapInit(Heap* php)
{assert(php);php->a = (HDataType*)malloc(sizeof(HDataType) * INIT_SZ);if (NULL == php->a){perror("malloc");return;}php->size = 0;php->capacity = INIT_SZ;
}//销毁
void HeapDestroy(Heap* php)
{assert(php);free(php->a);php->a = NULL;php->size = php->capacity = 0;
}
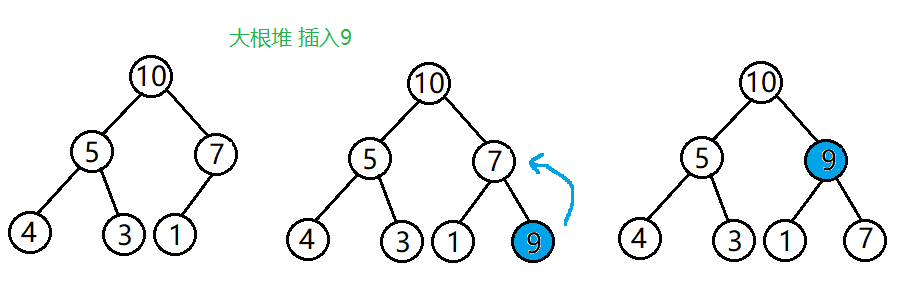
4.堆的插入
堆的插入需要用到向上调整算法。
实现步骤:
1.在堆的末尾插入一个元素;
2.该元素向上调整,直到满足堆的性质。
//入堆
void HeapPush(Heap* php, HDataType x)
{assert(php);//扩容if (php->size == php->capacity){HDataType* tmp = (HDataType*)realloc(php->a, sizeof(HDataType) * (INC_SZ + php->capacity));if (NULL == tmp){perror("malloc");return;}php->a = tmp;php->capacity += INC_SZ;}php->a[php->size++] = x;//尾插AdjustUp(php->a, php->size - 1);//向上调整
}
5.堆的删除
删除的是堆顶的元素,删除之后仍然保证是堆
堆的删除需要用到向下调整算法。
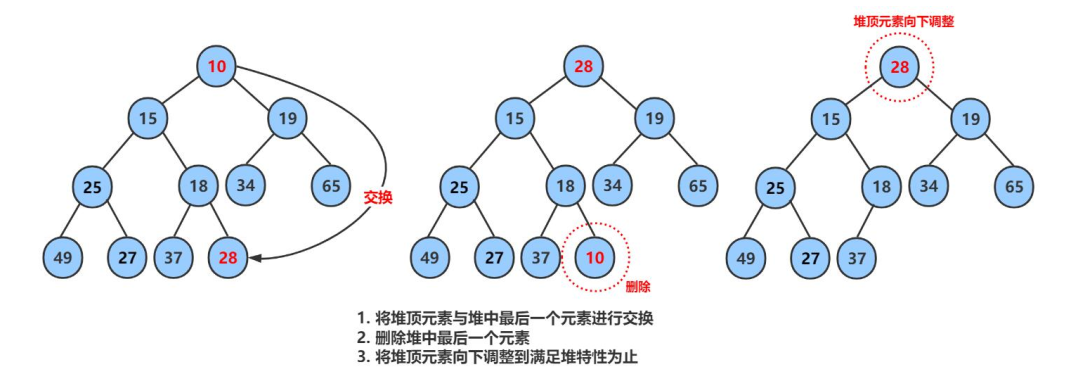
实现步骤:
1.将堆顶元素与最后一个元素交换;
2.堆长度-1,即删除最后一个位置;
3.将交换后的堆顶元素向下调整。
void HeapPop(Heap* php)
{assert(php);assert(!HeapEmpty(php));//将尾数据和堆顶数据交换,交换后的堆顶元素再向下调整Swap(&php->a[php->size - 1], &php->a[0]);php->size--;//堆的有效长度-1AdjustDown(php->a, 0, php->size);
}
6.堆的其他操作
//返回堆顶元素
HDataType HeapTop(Heap* php)
{assert(php);return php->a[0];
}
//判堆空
bool HeapEmpty(Heap* php)
{assert(php);return php->size == 0;
}
//堆的元素个数
int HeapSize(Heap* php)
{assert(php);return php->size;
}
三、堆的应用
1.堆排序
从前面的学习我们知道,堆结构的层序遍历,也就是从上到下每一层的从左到右,并非是有序的,也就是说堆存储在数组中的数据并不是有序的。比如下面这个大根堆,在数组中就是10,5,9,4,3,1,7 我们如何利用堆的特性将这些数据排序呢?
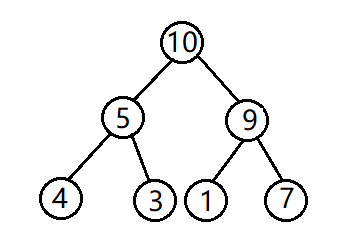
我们知道,大根堆的堆顶一定是最大的,小根堆的堆顶一定是最小的,所以利用这一个特点,我们可以取出堆顶元素,然后将剩下的元素重新调整成堆,再取堆顶元素,再调整剩下的元素,依次类推直到最后一个元素,就可以实现堆排序了。
但是,如果我们将堆顶元素按兵不动,将剩下的元素原地调整成堆,但剩下的元素会被完全打乱,完全不符合堆的性质,需要重新建堆,最后虽然也可以排序,但是效率却很低。这样的话跟普通排序没什么区别,每次找最大值(最小值)就好了,并没有用到堆的优势。
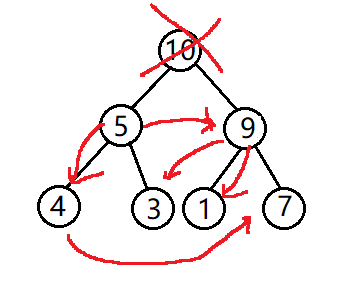
堆排序的实现步骤:
1.先将数组建堆;
2.将堆顶元素与堆末尾元素交换;
3.堆有效长度-1;
4.再将堆顶元素向下调整,直到调整到成堆
这不就是先建一个堆,再进行堆的删除操作吗?没毛病,原理是一样的。
比如一个大根堆,我们取出堆顶元素(最大数)与最后一个数交换,交换后的最大数不看作在堆里面,那么堆顶元素的左右子树仍满足堆的性质,堆的结构并没有被破坏,然后堆顶元素向下调整成堆,即可选出第二大的数,以此类推到最后一个元素,就可以成功实现堆排序了。
堆排序就是每次将堆顶元素从数组的末尾往前放,所以排升序建大堆,排降序建小堆
//堆排序
void HeapSort(int* a, int n)
{//建堆:排升序建大堆,排降序建小堆//倒着调整,从最后一个非叶子结点开始向下调整建堆 效率O(N)for (int i = (n - 1 - 1) / 2; i >= 0; i--){AdjustDown(a, i, n);}//O(N*logN)int end = n - 1;//堆的有效长度while (end > 0){Swap(&a[0], &a[end]);AdjustDown(a, 0, end);end--;}
}
堆排序的时间复杂度是O(N*logN)
2.Top-K问题
Top-K问题:求集合中前K个最大的元素或者最小的元素,一般情况下数据量都比较大。
比如:游戏中排行榜前50名,全校前10名等。
对于Top-K问题,自然第一个想到的就是排序,没毛病。但是数据量很大的情况下,排序就不太可取了(可能
数据都不能一下子全部加载到内存中)。
第二种方法就是用堆来解决。
实现方法:
- 用数据集合中前K个元素来建堆。
前k个最大的元素,则建小堆
前k个最小的元素,则建大堆- 用剩余的N-K个元素依次与堆顶元素来比较,不满足则替换堆顶元素。比较完后,堆中剩余的K个元素就是所求的前K个最小或者最大的元素。
如果选前k个最大值,需要建小堆。
原理分析:小堆的堆顶元素是这k个数据中最小的元素,如果剩下N-K个元素中有大于堆中最小值的,说明这个数可以进入前k名;如果剩下N-K个元素中有小于堆中最小值的,则无法进入前k名。但是如果建大堆的话,堆顶元素就无法作为标准了。
void TopK(int* a, int n, int k)
{//用a中前k个元素建堆for (int i = (k - 2) / 2; i >= 0; i--)AdjustDown(a, i, k);for (int i = k; i < n; i++){if (a[i] < a[0]){Swap(&a[i], &a[0]);//不满足则交换AdjustDown(a, 0, k);//向下调整}}for (int i = 0; i < k; i++)printf("%d ", a[i]);
}
上述代码只是选出前k个最大值或最小值,并没有将这k个数排序,如果要实现排序功能自行添加即可。
堆的完整代码放在gitee:https://gitee.com/ncu-ball/study/tree/master/24_4_19
相关文章:

【数据结构】堆(Heap)
文章目录 一、堆的概念及结构二、堆的实现1.向上调整算法2.向下调整算法3.堆的创建4.堆的插入5.堆的删除6.堆的其他操作 三、堆的应用1.堆排序2.Top-K问题 一、堆的概念及结构 堆(Heap)是一种特殊的非线性结构。堆中的元素是按完全二叉树的顺序存储方式存储在数组 中。满足任意…...
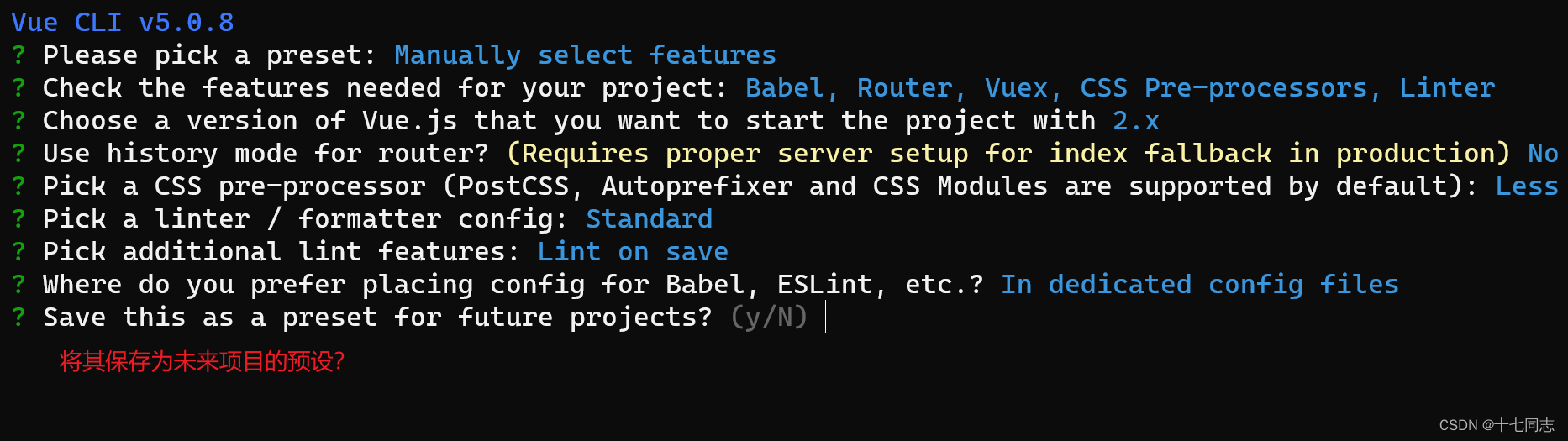
vue cli 自定义项目架子,vue自定义项目架子,超详细
脚手架Vue CLI基本介绍: Vue CLI 是Vue官方提供的一个全局命令工具 可以帮助我们快速创建一个开发Vue项目的标准化基础架子【集成了webpack配置】 脚手架优点: 开箱即用,零配置内置babel等工具标准化的webpack配置 脚手架 VueCLI相关命令…...

flink cdc,读取datetime类型
:flink cdc,读取datetime类型,全都变成了时间戳 Flink CDC读取MySQL的datetime类型时会转换为时间戳的问题,可以通过在Flink CDC任务中添加相应的转换器来解决。具体来说,可以在MySQL数据源的debezium.source.converter配置项中指…...

Kotlin 编译器和工具链:深入解析与实践案例
Kotlin 编译器和工具链是构建 Kotlin 项目的核心组件,它们负责将 Kotlin 代码转换为可在 JVM 或 JavaScript 环境中运行的代码。本文将详细介绍 Kotlin 编译器和工具链的工作原理、使用方法,以及在实际开发中的应用案例。 1. 引言 Kotlin 作为一种现代…...

kettle
文章目录 读取共享数据库连接报错 读取共享数据库连接报错 读取共享数据库连接报错 解决方法:修改共享文件中的中文字符,文件位置一般是默认的:C:\Users\Administrator.kettle。将shared.xml文件中的中文字符改成英文后问题就解决了。...
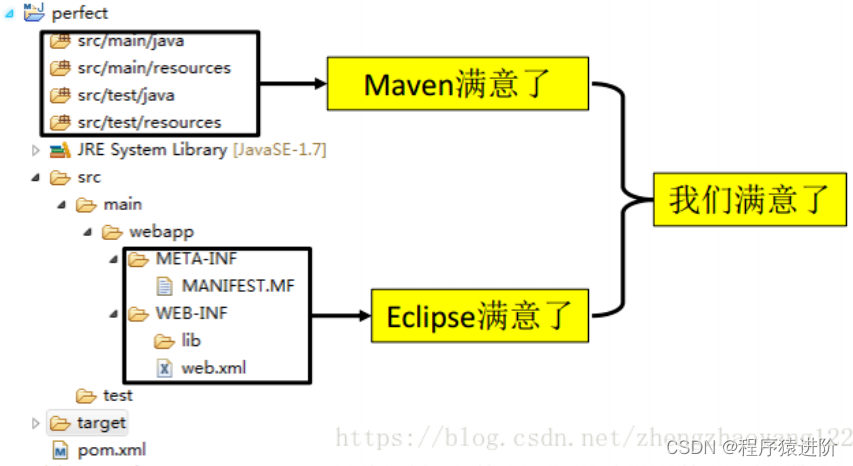
Maven 自动化构建
优质博文:IT-BLOG-CN 一、Maven:是一款服务于 Java平台的自动化构建工具 【1】Maven可以将一个项目按模块划分成不同的工程,利于分工协作; 【2】Maven可以将 jar包保存在自己的中央“仓库”中进行统一管理,有需要使用的工程引用这…...

Unicode字符集和UTF编码
文章目录 前言一、字符集和编码方式二、unicode字符集utf32编码utf8编码utf8编码函数示例utf8解码函数示例 utf16编码utf16编码解码函数示例 总结 前言 本文详细介绍 u n i c o d e unicode unicode 字符集和其相关的三种编码方式: u t f 8 utf8 utf8,…...

echarts默认图例(横线+圈圈)
修改echarts 图例样式 项目里折线图需要去掉圆点, 但是图例样式需要是默认样式(横线和圈圈) 原始代码:(只展示series 和legend配置 ) series: [{name: chartObj.names[ind_one],yAxisIndex: yIndex,type: ele_one,barMaxWidth: 15,tooltip: {show: true},data: chartObj.yAx…...
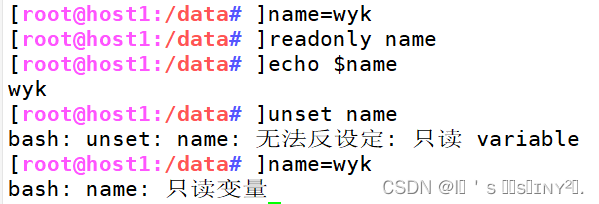
Shell脚本的基础和变量
1.shell脚本基础 1.1 shell的作用 Linux 系统中的 Shell 是一个特殊的应用程序,它介于操作系统内核与用户之间,充当 了一个“命令解释器”的角色,负责接收用户输入的操作指令(命令)并进行解释,将需要执 行的…...
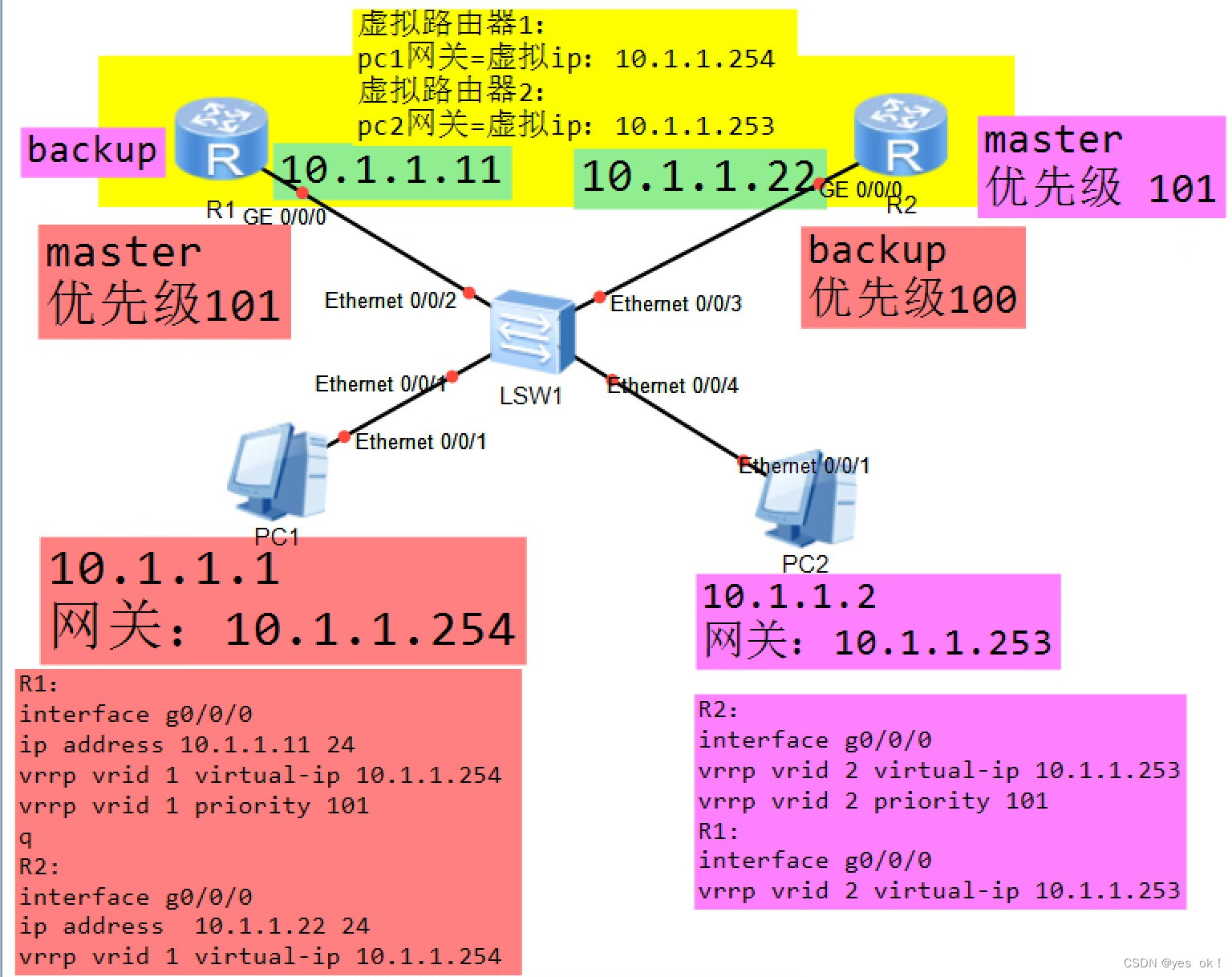
VRRP协议-负载分担配置【分别在路由器与交换机上配置】
VRRP在路由器与交换机上的不同配置 一、使用路由器实现负载分担二、使用交换机实现负载分担一、使用路由器实现负载分担 使用R1与R2两台设备分别进行VRRP备份组 VRRP备份组1,虚拟pc1的网关地址10.1.1.254 VRRP备份组2,虚拟pc2的网关地址10.1.1.253 ①备份组1的vrid=1,vrip=…...
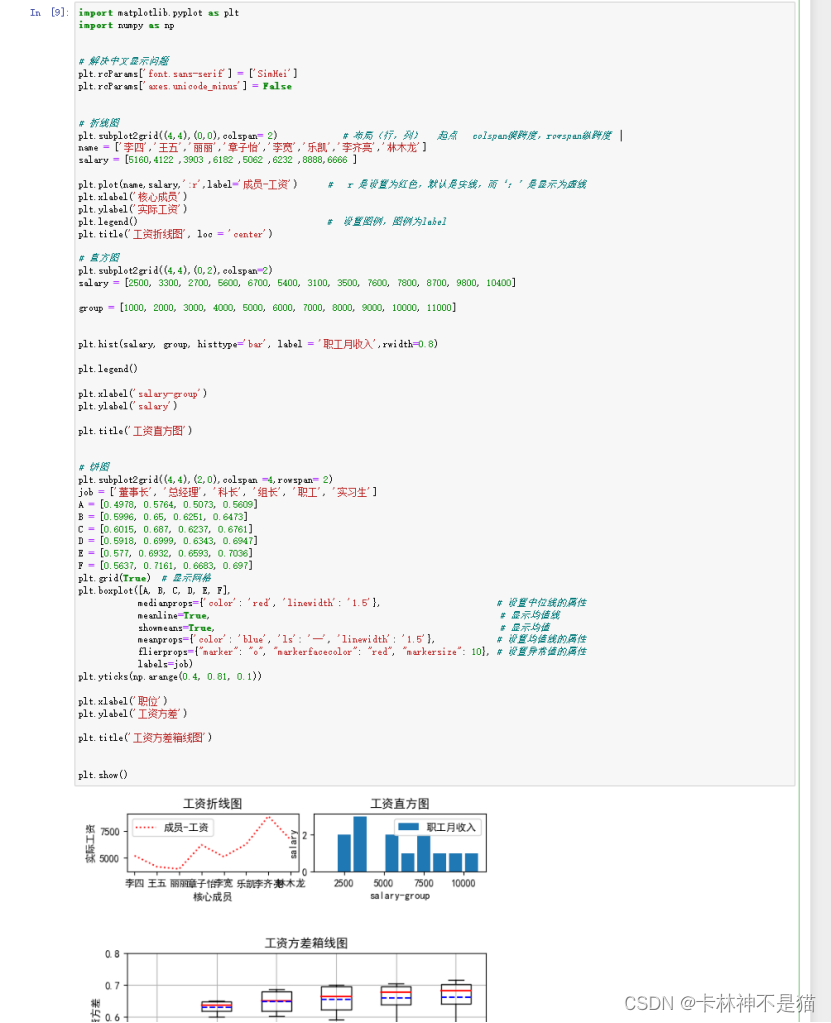
商务分析方法与工具(十):Python的趣味快捷-公司财务数据最炫酷可视化
Tips:"分享是快乐的源泉💧,在我的博客里,不仅有知识的海洋🌊,还有满满的正能量加持💪,快来和我一起分享这份快乐吧😊! 喜欢我的博客的话,记得…...
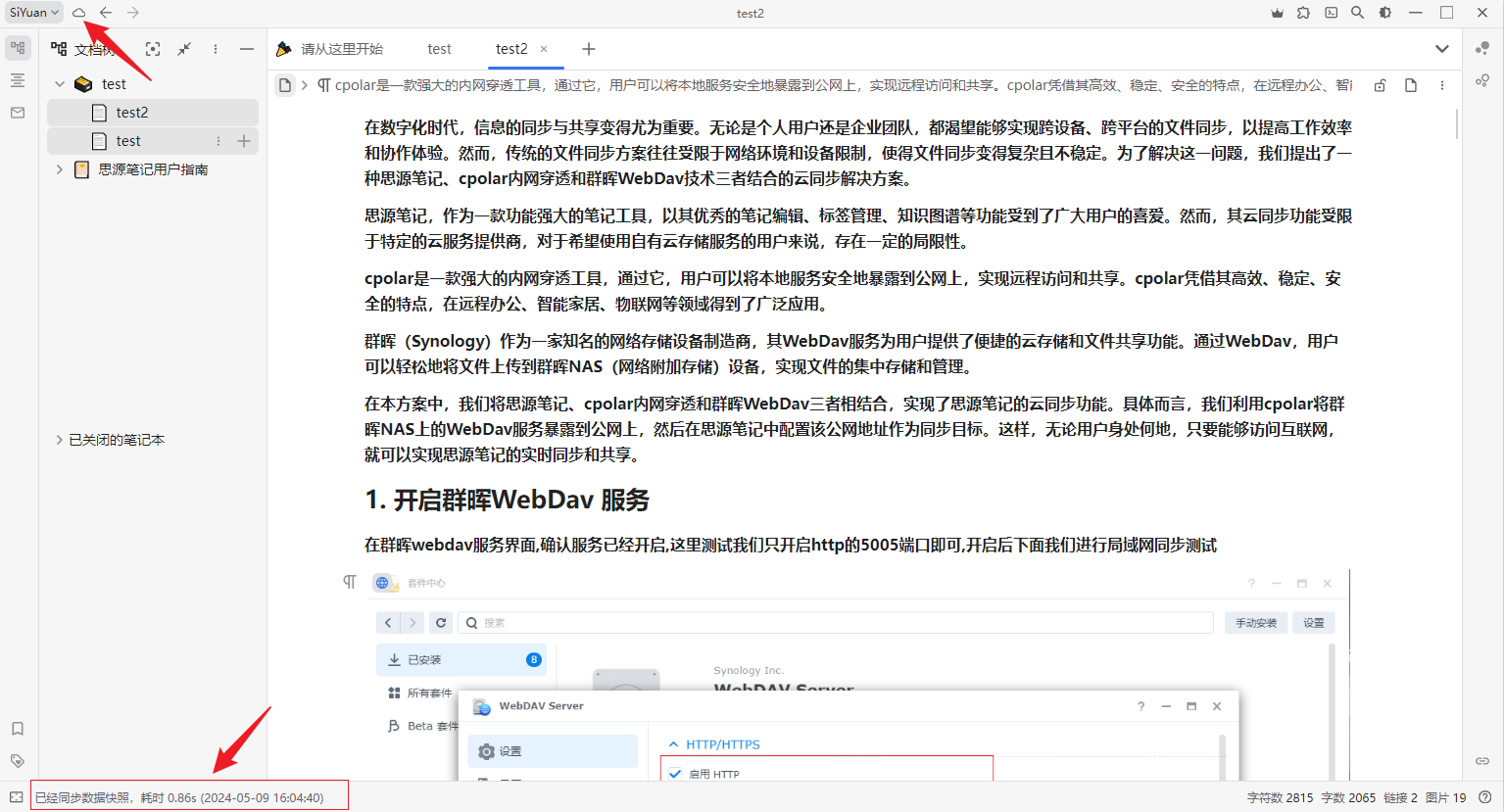
思源笔记如何结合群晖WebDav实现云同步数据
文章目录 1. 开启群晖WebDav 服务2. 本地局域网IP同步测试3. 群晖安装Cpolar4. 配置远程同步地址5. 笔记远程同步测试6. 固定公网地址7. 配置固定远程同步地址 在数字化时代,信息的同步与共享变得尤为重要。无论是个人用户还是企业团队,都渴望能够实现跨…...
)
Electron Forge | 跨平台实战详解(中)
简介 上篇 介绍了 Electron 和 Electron Builder 的基本用法,本篇将介绍更常用也更方便的打包工具,Electron Forge 。 Electron Forge 是一个为 Electron 应用的开发、打包和分发而设计的全功能工具集。它整合了多个底层 Electron 工具到一个统一的命令…...

stable diffusion教程
Stable Diffusion 是一种流行的图像生成模型,它可以根据文本提示生成高质量的图片。如果你想了解如何使用 Stable Diffusion,这里有一些基本的步骤和资源,可以帮助你开始使用: ### 1. 安装 Stable Diffusion 首先,你需…...
)
音频文件分析-- whisper(python 文档解析提取)
使用whisper转文本,这里使用的是large-v3版本 pip install githttps://github.com/openai/whisper.git import whisper import os from tqdm import tqdmmodel whisper.load_model("large-v3")path "rag_data" for fi in tqdm(os.listdir(pa…...
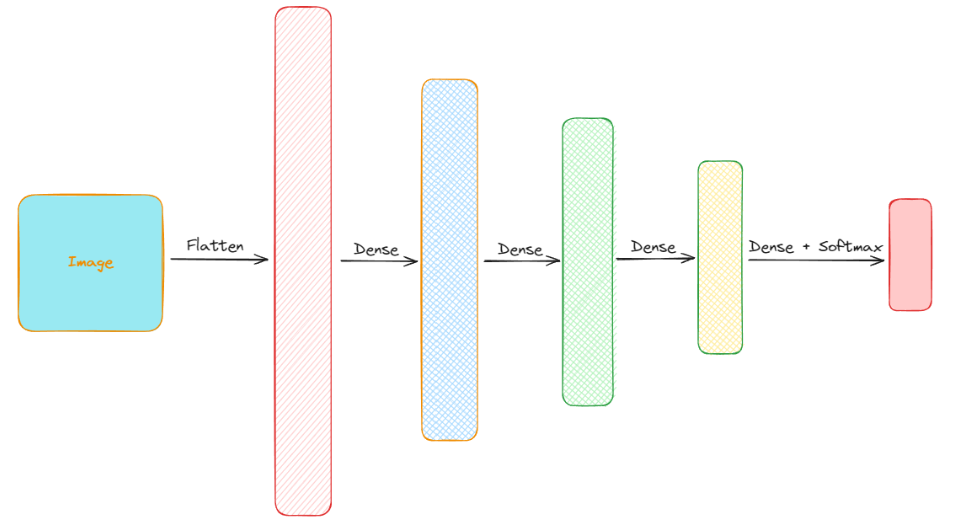
Python深度学习基于Tensorflow(3)Tensorflow 构建模型
文章目录 数据导入和数据可视化数据集制作以及预处理模型结构低阶 API 构建模型中阶 API 构建模型高阶 API 构建模型保存和导入模型 这里以实际项目CIFAR-10为例,分别使用低阶,中阶,高阶 API 搭建模型。 这里以CIFAR-10为数据集,C…...
火爆多年的抖音小店,2024年想要入驻需要什么条件呢?
大家好,我是电商糖果 我相信现在只要会上网的年轻人,对抖音小店一定不会感觉陌生。 它最近几年的风头,可是远远超过某宝,某多多了。 不少抖音用户也有了在抖音购物的习惯,现在的抖音上入驻了上百万家电商商家。 这…...
STM32G030C8T6:EEPROM读写实验(I2C通信)
本专栏记录STM32开发各个功能的详细过程,方便自己后续查看,当然也供正在入门STM32单片机的兄弟们参考; 本小节的目标是,系统主频64 MHZ,采用高速外部晶振,实现PB11,PB10 引脚模拟I2C 时序,对M24C08 的EEPRO…...
使用Git管理github的代码库-上
1、下载安装Git https://download.csdn.net/download/notfindjob/11451730?spm1001.2014.3001.5503 2、注册一个github的账号(已经注册的,可略过这一步) 3、打开git命令行,配置github账号 git config --global user.name &quo…...
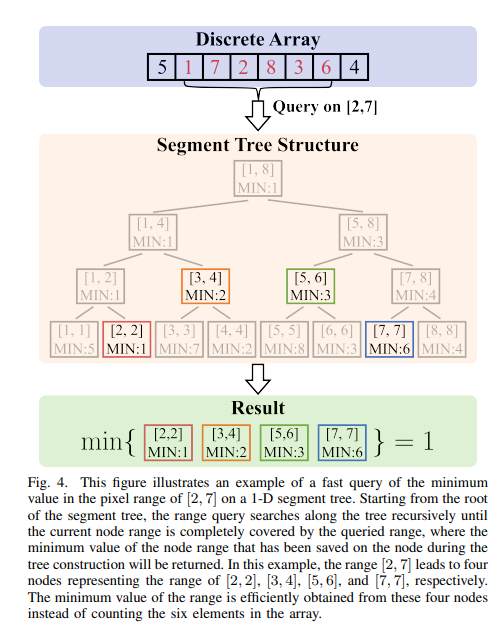
经典文献阅读之--D-Map(无需射线投射的高分辨率激光雷达传感器的占据栅格地图)
0. 简介 占用地图是机器人系统中推理环境未知和已知区域的基本组成部分。《Occupancy Grid Mapping without Ray-Casting for High-resolution LiDAR Sensors》介绍了一种高分辨率LiDAR传感器的高效占用地图框架,称为D-Map。该框架引入了三个主要创新来解决占用地图…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...

Selenium常用函数介绍
目录 一,元素定位 1.1 cssSeector 1.2 xpath 二,操作测试对象 三,窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四,弹窗 五,等待 六,导航 七,文件上传 …...

Git常用命令完全指南:从入门到精通
Git常用命令完全指南:从入门到精通 一、基础配置命令 1. 用户信息配置 # 设置全局用户名 git config --global user.name "你的名字"# 设置全局邮箱 git config --global user.email "你的邮箱example.com"# 查看所有配置 git config --list…...