react 逻辑 AND 运算符 ()
在 React 组件中,当你想在条件为 true 时渲染一些 JSX 时,它经常会出现,或者什么都不渲染。使用 ,只有在以下情况下才能有条件地呈现复选标记:&&isPackedtrue
return (<li className="item">{name} {isPacked && '✔'}</li>
);您可以将其理解为“if isPacked, then (&&) render the checkmark, else , render nothing ”。
这是在行动:
function Item({ name, isPacked }) {return (<li className="item">{name} {isPacked && '✔'}</li>);
}export default function PackingList() {return (<section><h1>Sally Ride's Packing List</h1><ul><Item isPacked={true} name="Space suit" /><Item isPacked={true} name="Helmet with a golden leaf" /><Item isPacked={false} name="Photo of Tam" /></ul></section>);
}如果 JavaScript 的左侧(我们的条件)为 ,则 JavaScript && 表达式返回其右侧的值(在本例中为复选标记)。但是如果条件是 ,则整个表达式变为 。React 将其视为 JSX 树中的一个“洞”,就像 或 一样,并且不会在其位置上渲染任何东西。truefalsefalsefalsenullundefined
不要将数字放在
&&. 的左侧。为了测试条件,JavaScript 会自动将左侧转换为布尔值。但是,如果左侧是 ,那么整个表达式都会得到该值 (),并且 React 会很乐意渲染而不是什么都没有。
000例如,一个常见的错误是编写类似 .很容易假设它在 is 时什么都不渲染,但它确实渲染了它本身!
messageCount && <p>New messages</p>messageCount00要修复它,请将左侧设为布尔值:。
messageCount > 0 && <p>New messages</p>
有条件地将 JSX 分配给变量
当快捷方式妨碍编写纯代码时,请尝试使用语句和变量。您可以重新分配使用 let 定义的变量,因此首先提供要显示的默认内容,即名称:if
let itemContent = name; 使用语句将 JSX 表达式重新赋值给 if :ifitemContentisPackedtrue
if (isPacked) { itemContent = name + " ✔"; } 大括号打开“JavaScript 之窗”。在返回的 JSX 树中嵌入带有大括号的变量,将先前计算的表达式嵌套在 JSX 中:
<li className="item"> {itemContent} </li> 这种风格是最冗长的,但也是最灵活的。这是在行动:
function Item({ name, isPacked }) {let itemContent = name;if (isPacked) {itemContent = name + " ✔";}return (<li className="item">{itemContent}</li>);
}export default function PackingList() {return (<section><h1>Sally Ride's Packing List</h1><ul><Item isPacked={true} name="Space suit" /><Item isPacked={true} name="Helmet with a golden leaf" /><Item isPacked={false} name="Photo of Tam" /></ul></section>);
}相关文章:
)
react 逻辑 AND 运算符 ()
在 React 组件中,当你想在条件为 true 时渲染一些 JSX 时,它经常会出现,或者什么都不渲染。使用 ,只有在以下情况下才能有条件地呈现复选标记:&&isPackedtrue return (<li className"item">{…...
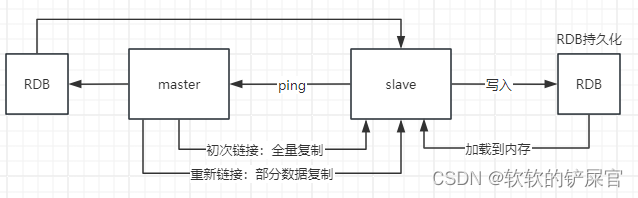
Redis详解(二)
事务 什么是事务? 事务是一个单独的隔离操作:事务中的所有命令都会序列化、按顺序地执行。事务在执行的过程中,不会被其他客户端发送来的命令请求所打断。 事务是一个原子操作:事务中的命令要么全部被执行,要么全部都…...

嵌入式:基于STM32的智能家居照明控制系统
在智能家居系统中,自动照明控制不仅提高了居住舒适度,还有助于节能减排。本教程旨在引导读者通过使用STM32微控制器来开发一个智能照明控制系统。该系统能够根据环境光线自动调整室内照明的亮度,并支持通过简单的用户界面手动控制光线。 一、…...

三种基本排序-冒泡,选择,二分
闲话不多说,直接上代码,简明易懂,条理清晰,交互性强,尽善尽美 码住,建议copy下来: 先上二分法吧,稍复杂点的,代码多一些,用了函数调用 二分排序࿱…...

windows查找重复的物理地址
单独查询所有物理(mac)地址(cmd执行):arp -a 查找同一局域网下重复的mac,打开power shell执行以下命令: Get-NetNeighbor | Where-Object { $_.State -eq "Reachable" } | Select-O…...
-shell脚本应用(三))
linux进阶高级配置,你需要知道的有哪些(8)-shell脚本应用(三)
1、for循环语句的结构: for 变量名 in 取值列表 do 命令序列 done 2、while循环语句结构: while 条件测试 do 命令序列 done 3、for和while的区别 for:控制循环来自于取值列表 while:控制循环来自于条件测试 4、case语句的…...

安全测试|常见SQL注入攻击方式、影响及预防
SQL注入 什么是SQL注入? SQL注入是比较常见的网络攻击方式之一,主要攻击对象是数据库,针对程序员编写时的疏忽,通过SQL语句,实现无账号登录,篡改数据库。 SQL注入简单来说就是通过在表单中填写包含SQL关键…...
【Git】Git在Gitee上的基本操作指南
文章目录 1. 查看 git 版本2. 从Gitee克隆仓库:3. 复制文件到工作目录:4. 将未跟踪的文件添加到暂存区:5. 在本地提交更改:6. 将更改推送到远程仓库(Gitee):7. Windows特定提示: 1. …...
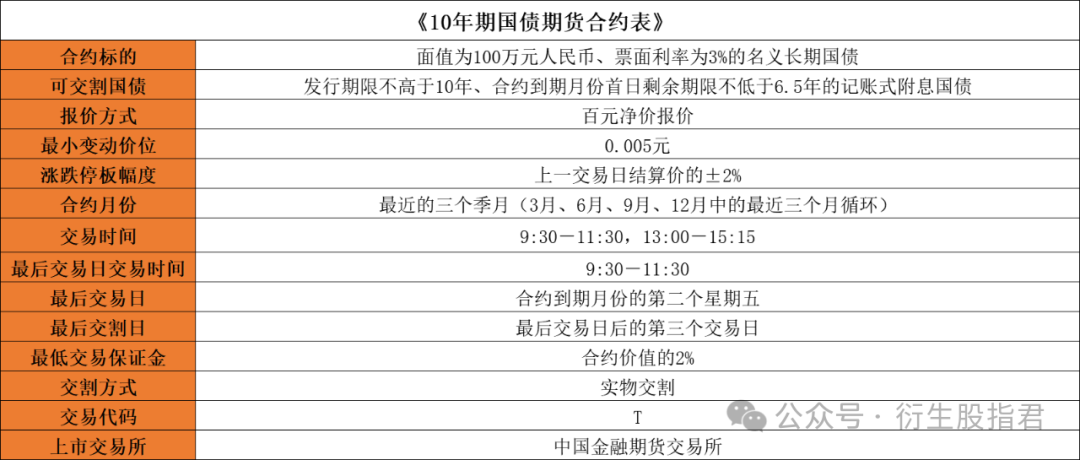
国债期货怎么买?十年国债交易手册
国债,简单来说,就是国家为了筹集资金而向大众借钱的一种方式。国家通过发行债券,向投资者承诺在约定的时间里支付利息,并在到期时归还本金。因为是国家发行的,所以国债的信用等级非常高,通常被认为是非常安…...
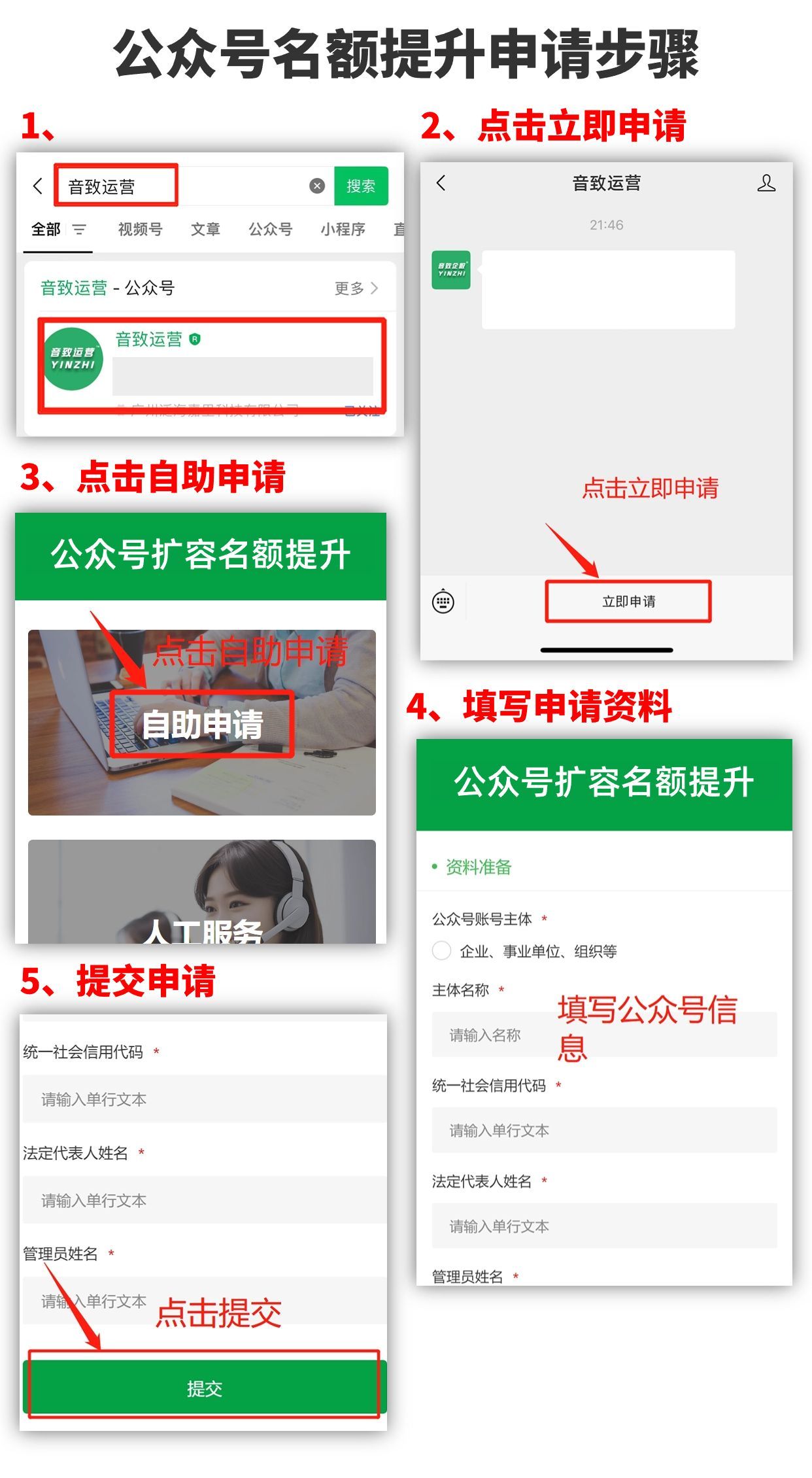
公司申请增加公众号数量
一般可以申请多少个公众号?众所周知,在2013年前后,公众号申请是不限制数量的,后来企业开始限制申请50个,直到2018年的11月tx又发布,其中个人主体可申请公众号由2个调整为1个,企业主体由50个调整…...

什么是.faust勒索病毒?应该如何防御?
faust勒索病毒详细介绍 faust勒索病毒是一种新型的勒索软件,最早出现在2018年。该病毒通过加密计算机系统中的文件并要求支付赎金来解锁文件,从而获取经济利益。与传统的勒索软件相比,faust勒索病毒采用了更加先进的加密算法和隐藏技术&#…...
邓闲小——生存、生活、生命|真北写作
人生有三个层次∶生存、生活、生命。 生存就是做必须做的事。生存的模式是邓,是交易,是买卖。别人需要的东西,你生产出来,卖给他。哪怕这个东西没啥用,也可以卖,情绪也可以卖。你需要的东西,你花…...

品牌舆情都包含什么内容?建议收藏
一个品牌的声誉、形象、产品质量、服务质量等,无时无刻不在接受着大众的检验。互联网传播迅速,一个不好的舆论直接导致整个品牌的声誉受到严重影响。品牌舆情都包含什么内容?接下来伯乐网络传媒就来给大家讲一讲。 一、品牌舆情的基本构成 1…...
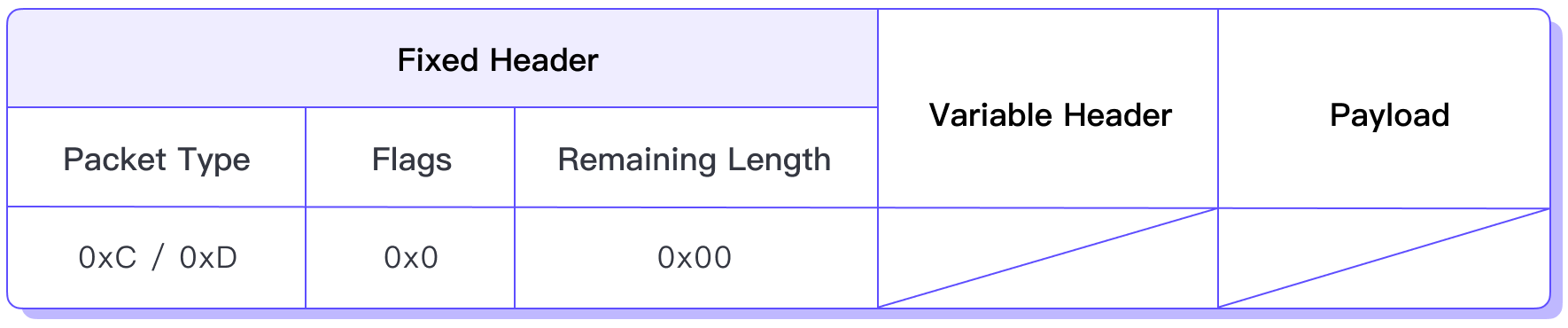
MQTT 5.0 报文解析 04:PINGREQ 与 PINGRESP
欢迎阅读 MQTT 5.0 报文系列 的第四篇文章。在上一篇中,我们已经介绍了 MQTT 5.0 中的 SUBSCRIBE 报文和 UNSUBSCRIBE 报文。现在,我们将介绍用于维持连接的控制报文:PINGREQ 和 PINGRESP。 除了用于连接、发布和订阅的控制报文,…...

【算法刨析】完全背包
完全背包与01背包的区别 01背包对于一个物品只能选择一次,但是完全背包可以选择任意次; 思路 和01背包类似,01背包我们只需要判断选或不选,完全背包也是如此,不同的是,对于这个物品我们在判断选后在增加一…...
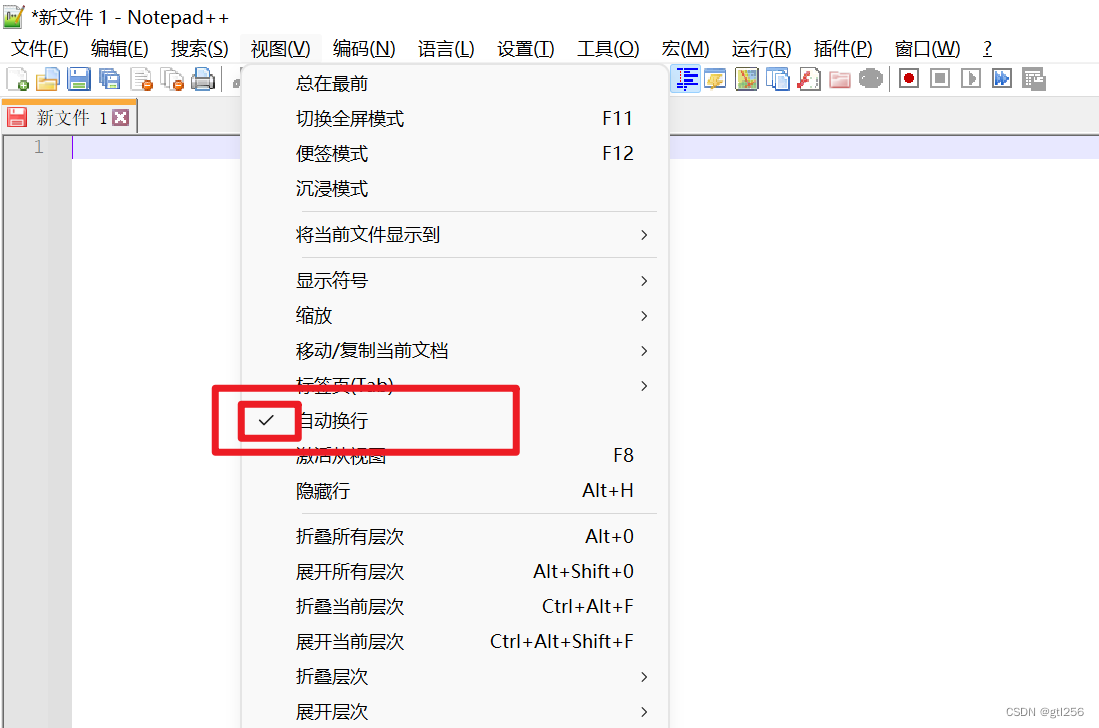
notepad++
文章目录 换行 换行 根据需要选择是否要自动换行或者一行展示。 点击视图 选中或者取消选中自动换行...
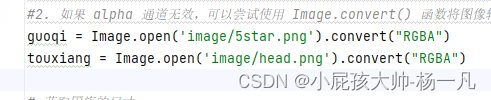
Python ValueError: bad transparency mask
修改前 修复后 运行正常 from PIL import Image# 读取图片 #报错信息解决ValueError: bad transparency mask--相关文档地址https://blog.csdn.net/kalath_aiur/article/details/103945309 #1. 检查 alpha 通道是否是一个有效的掩码。如果不是,则需要对 alpha 通道…...

Linux本地部署Nightingale夜莺监控并实现远程访问提高运维效率
💝💝💝欢迎来到我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:kwan 的首页,持续学…...
开关电源功率测试方法:输入、输出功率测试步骤
在现代电子设备中,开关电源扮演着至关重要的角色,其效率和稳定性直接影响到整个系统的性能。因此,对开关电源进行功率测试成为了电源管理的重要环节。本文将详细介绍如何使用DC-DC电源模块测试系统对开关电源的输入输出功率进行准确测量&…...

QT 文字转语言插件
1.在工程.pro文件中添加 QT texttospeech 2.在头文件中添加 #include <QTextToSpeech> 3.使用的方法 QString str"欢迎使用智慧教育学习平台";QTextToSpeech *Speechernew QTextToSpeech;const QVector<QVoice> voices Speecher->availableV…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...

MFC 抛体运动模拟:常见问题解决与界面美化
在 MFC 中开发抛体运动模拟程序时,我们常遇到 轨迹残留、无效刷新、视觉单调、物理逻辑瑕疵 等问题。本文将针对这些痛点,详细解析原因并提供解决方案,同时兼顾界面美化,让模拟效果更专业、更高效。 问题一:历史轨迹与小球残影残留 现象 小球运动后,历史位置的 “残影”…...

Golang——9、反射和文件操作
反射和文件操作 1、反射1.1、reflect.TypeOf()获取任意值的类型对象1.2、reflect.ValueOf()1.3、结构体反射 2、文件操作2.1、os.Open()打开文件2.2、方式一:使用Read()读取文件2.3、方式二:bufio读取文件2.4、方式三:os.ReadFile读取2.5、写…...
