[动态规划] 完美覆盖
描述
一张普通的国际象棋棋盘,它被分成 8 乘 8 (8 行 8 列) 的 64 个方格。设有形状一样的多米诺牌,每张牌恰好覆盖棋盘上相邻的两个方格,即一张多米诺牌是一张 1 行 2 列或者 2 行 1 列的牌。那么,是否能够把 32 张多米诺牌摆放到棋盘上,使得任何两张多米诺牌均不重叠,每张多米诺牌覆盖两个方格,并且棋盘上所有的方格都被覆盖住?我们把这样一种排列称为棋盘被多米诺牌完美覆盖。这是一个简单的排列问题,同学们能够很快构造出许多不同的完美覆盖。但是,计算不同的完美覆盖的总数就不是一件容易的事情了。不过,同学们 发挥自己的聪明才智,还是有可能做到的。
现在我们通过计算机编程对 3 乘 n 棋盘的不同的完美覆盖的总数进行计算。
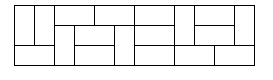
任务
对 3 乘 n 棋盘的不同的完美覆盖的总数进行计算。
输入
一次输入可能包含多行,每一行分别给出不同的 n 值 ( 即 3 乘 n 棋盘的列数 )。当输入 -1 的时候结束。
n 的值最大不超过 30.
输出
针对每一行的 n 值,输出 3 乘 n 棋盘的不同的完美覆盖的总数。
样例输入
2 8 12 -1
样例输出
3 153 2131
解题分析
首先,由于多米诺牌本身占两个格子,所以如果完全覆盖的话,那么n一个要偶数,否则3乘上一个奇数会导致格子总数为奇数,这就矛盾了。
然后,我们可以明显地感知到,我们当前排列的结果与前面的排列是有一定关系的。我们先计算一个n=2的时候,这是最小的单元(n=1的时候很明显,不可能被完全覆盖,或者从n必须为偶数理解)。我们自己脑子里摆一摆,知道n=2的时候有三种摆法。现在我们设置一个数组dp,dp[i]表示n=i时的摆法。显然,dp[i]中有一部分摆法是3*dp[i-2]。但是这显然没有包括全部的情况。那我们还漏掉了哪些情况?
简单举个例子,有两种很重要的情况被我们忽略了。比如n=4的时候,如果我们只是计算3*dp[2],那实际上我们在n=2,3这两列可以横着放多米诺牌。这部分被我们忽略了。所以我们还需要考虑dp[i-4],即我们空出四列出来,然后计算dp[i-4]*2,然后保持这两列横着放,继续i-=2,因为我们刚刚使用了dp[i-4],这是没有考虑i-4和i-5列横着放并且i-3和i-2列横着放的情况。
代码实现
#include <iostream>
using namespace std;
int dp[31]={0};int compute(int m){if(dp[m]) return dp[m];for(int i=4;i<=30;i++){dp[i]=dp[i-2]*3;for(int j=i-4;j>=0;j-=2){dp[i]+=dp[j]*2;}}return dp[m];
}int main(){int n;dp[0]=1;dp[2]=3;while(cin>>n){if(n==-1){break; }cout<<compute(n)<<endl;}return 0;
}相关文章:

[动态规划] 完美覆盖
描述 一张普通的国际象棋棋盘,它被分成 8 乘 8 (8 行 8 列) 的 64 个方格。设有形状一样的多米诺牌,每张牌恰好覆盖棋盘上相邻的两个方格,即一张多米诺牌是一张 1 行 2 列或者 2 行 1 列的牌。那么,是否能够把 32 张多米诺牌摆放…...
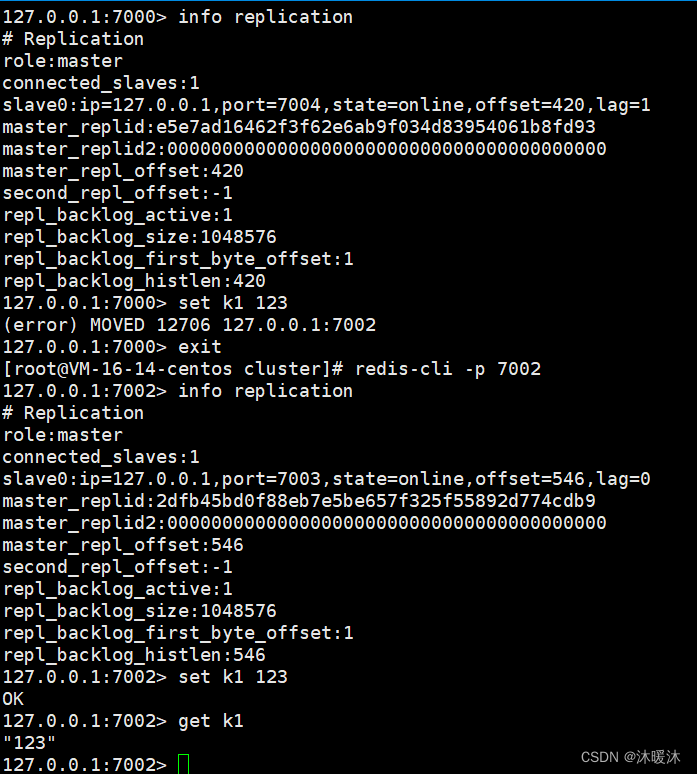
redis深入理解之实战
1、SpringBoot整合redis 1.1 导入相关依赖 <dependency><groupId>redis.clients</groupId><artifactId>jedis</artifactId> </dependency> <dependency><groupId>org.springframework.boot</groupId><artifactId&g…...

python设计模式---工厂模式
定义了一个抽象类Animal,并且让具体的动物类(Dog、Cat、Duck)继承自它,并实现了speak方法。然后创建了AnimalFactory工厂类,根据传入的参数来决定创建哪种动物的实例。 from abc import abstractmethod, ABCclass Anim…...

探索Vue 3.0中的v-html指令
探索Vue 3.0中的v-html指令 一、什么是v-html指令?1、 在Vue 3.0中使用v-html2、 注意事项 二、结语 一、什么是v-html指令? Vue.js作为一款流行的JavaScript框架,不断地演进着。随着Vue 3.0的发布,开发者们迎来了更加强大和灵活…...

anaconda 环境配置
官方网站下载地址: https://www.anaconda.com/download/ 国内清华镜像下载地址: https://mirrors.tuna.tsinghua.edu.cn/anaconda/archive/ 配置国内环境: conda config --add channels https://mirrors.tuna.tsinghua.edu.cn/anaconda/pkgs/free/ …...

DS:顺序表、单链表的相关OJ题训练(2)
欢迎各位来到 Harper.Lee 的学习世界! 博主主页传送门:Harper.Lee的博客主页 想要一起进步的uu欢迎来后台找我哦! 一、力扣--141. 环形链表 题目描述:给你一个链表的头节点 head ,判断链表中是否有环。如果链表中有某个…...
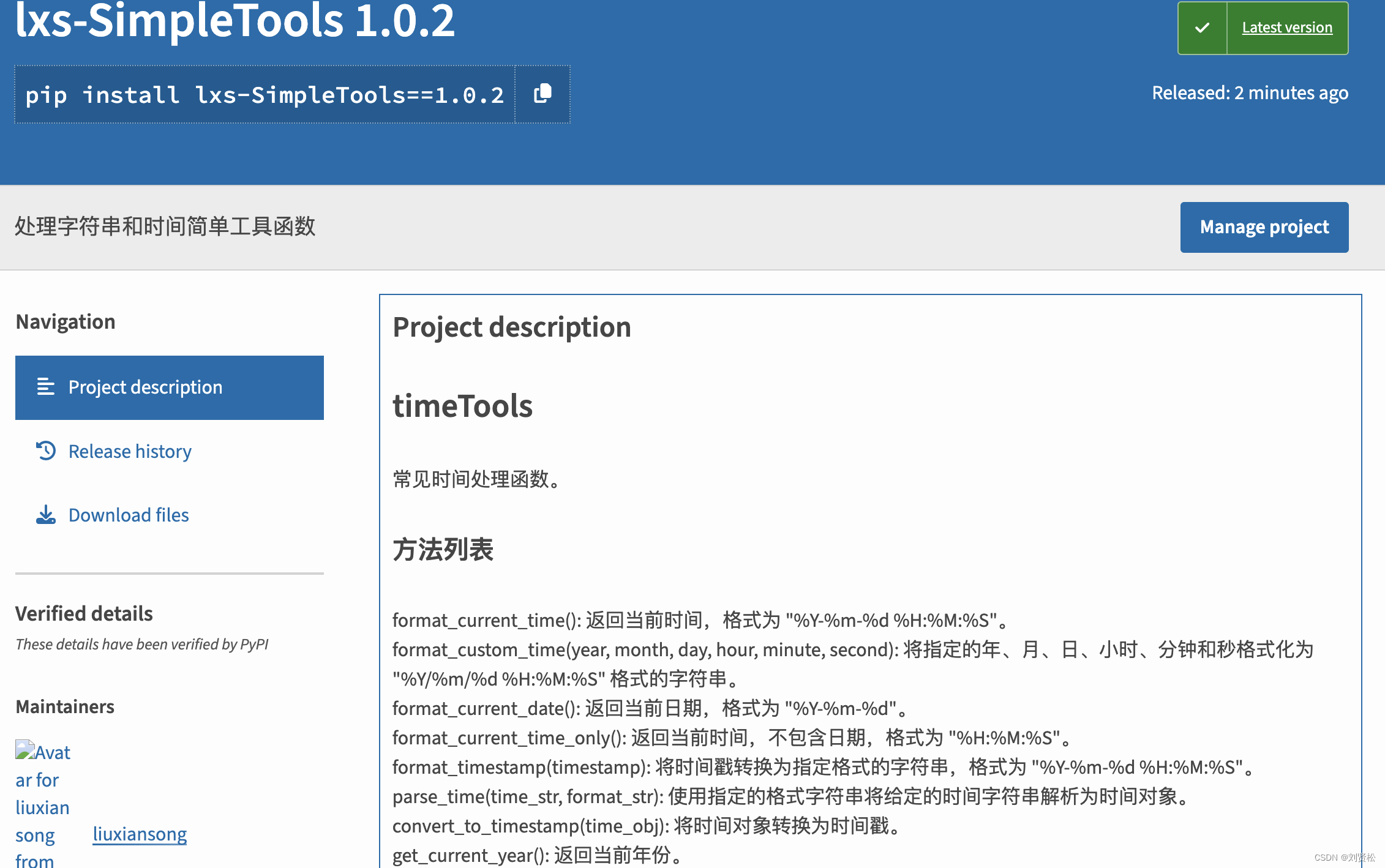
上传到 PyPI
将软件包上传到 PyPI(Python Package Index),您需要遵循以下步骤: 准备软件包:确保您的软件包满足以下要求: 包含一个 setup.py 文件,用于描述软件包的元数据和依赖项。包含软件包的源代码和必要…...
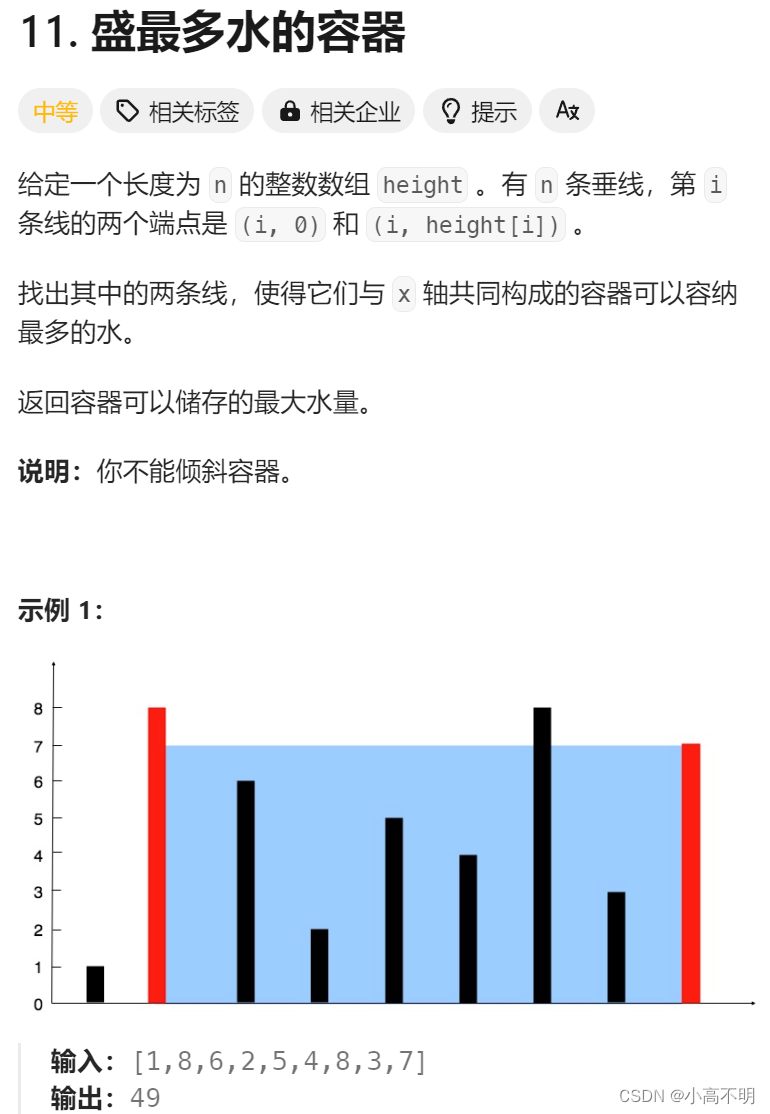
盛最多水的容器(双指针)
解题思路: 1,暴力解法(超时) 我们可以使用两层for循环进行遍历。找到那个最大的面积即可,这里我就不写代码了,因为写了也是超时。 2,双指针法 先定义两个指针一个在最左端,一个在…...
【深度学习】实验3 特征处理
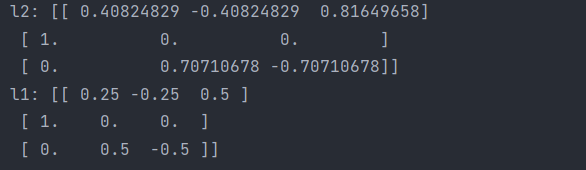
特征处理 python 版本 3.7 scikit-learn 版本 1.0.2 1.标准化 from sklearn.preprocessing import StandardScaler from sklearn.preprocessing import MinMaxScaler from matplotlib import gridspec import numpy as np import matplotlib.pyplot as plt cps np.random.…...
MoneyPrinter国内版改造
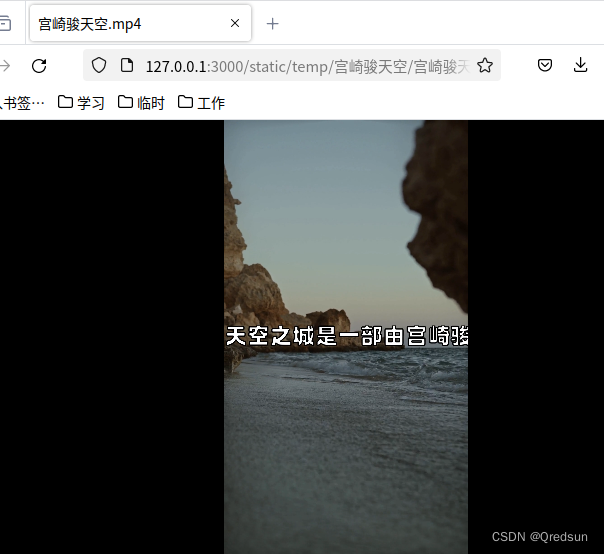
背景: MoneyPrinter 是一个自动生成短视频的开源项目。只需要输入短视频主题,然后就可以生成视频。 在国内环境运行时,框架中使用的youtube、抖音文字转语音等功能无法使用,需要对框架进行国内版改造,使其使用国内网络…...

C++ 派生类的引入与特性
一 继承与派生 从上面的例子可以看出: 继承:一旦指定了某种事物父代的本质特征,那么它的子代将会自动具有哪些性质。这就是一种朴素的可重用的概念。 派生:而且子代可以拥有父代没有的特性,这是可扩充的概念。 1 C 的…...
Poe是什么?怎样订阅Poe?
Poe(全称“开放探索平台”,Platform for Open Exploration)是一款由Quora开发的移动应用程序,于2022年12月推出。该应用程序内置建基于AI技术的聊天机器人,可供用户向机器人询问专业知识、食谱、日常生活,甚…...

基于FPGA的视频矩阵切换方案
一、单个显示设备的系统方案:会议室只有1个显示设备 会议室的信号源有很多,但是显示设备只有1个,这个时候最佳方案是使用切换器。 (1)切换器(控制方式:遥控器、软件、机箱面板、中控ÿ…...

.NET周刊【5月第1期 2024-05-05】
国内文章 一个开源轻量级的C#代码格式化工具(支持VS和VS Code) https://www.cnblogs.com/Can-daydayup/p/18164905 CSharpier是一个开源、免费的C#代码格式化工具,特点是轻量级且依赖Roslyn引擎重构代码格式。支持的IDE包括Visual Studio …...
springcloud -nacos实战
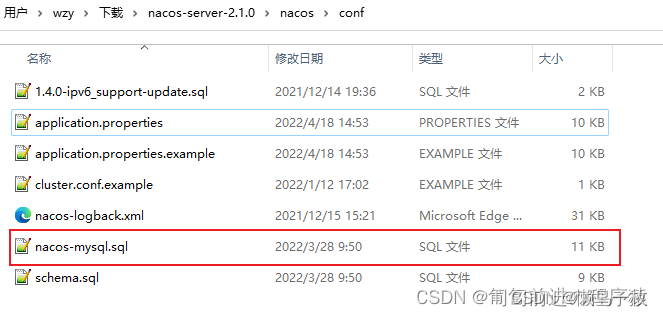
一、nacos 功能简介 1.1.什么是Nacos? 官方简介:一个更易于构建云原生应用的动态服务发现(Nacos Discovery )、服务配置(Nacos Config)和服务管理平台。 Nacos的关键特性包括: 服务发现和服务健康监测动态配置服务动态DNS服务服务及其元数…...

第十五章 数据管理成熟度评估练习
单选题 (每题1分,共19道题) 1、 [单选] 下列选项中属于数据管理成熟度2级特征的选项是? A:很少或没有治理;有限的工具集;单个竖井(系统)内定义角色;控件(如果有的话的应用完全不一致);未解决的数据质量问题 B:治理开始出现;引入一致的工具集;定义了一些角色和…...

tcpdump速查表
tcpdump 速查表 -D 列出网络设备 ~]$ sudo tcpdump -D1.eth02.nflog (Linux netfilter log (NFLOG) interface)3.nfqueue (Linux netfilter queue (NFQUEUE) interface)4.any (Pseudo-device that captures on all interfaces)5.lo [Loopback]-i 指定网卡 前面列出的设备可以…...

单元测试与集成测试:软件质量的双重保障
目录 概述 单元测试 集成测试 单元测试的方法 白盒测试 黑盒测试 白盒测试的方法和用例设计 代码审查 集成测试 单元测试工具 结语 在软件开发中,测试是一个不可或缺的环节,它能够帮助我们发现和修复缺陷,确保软件的质量和可靠性。…...
孙宇晨对话大公网:香港Web3政策友好环境示范意义重大
日前,全球知名华文媒体大公网发布《湾区web3大有可为》重磅系列报道。报道通过对中国香港与大湾区其他城市Web3政策、行业创新和生态建设等方面的梳理,以及对行业领袖和重要行业机构的走访,全面展现了在大湾区一体化发展的背景下,Web3等数字经济模式在该地区的长远发展潜力。 …...

Python运维之多线程!!
一、多线程 二、多线程编程之threading模块 2.1、使用threading进行多线程操作有两种方法: 三、多线程同步之Lock(互斥锁) 四、多线程同步之Semaphore(信号量) 五、多线程同步之Condition 六、多线程同步之Event…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...
