第五百零三回
文章目录
- 1. 概念介绍
- 2. 使用方法
- 2.1 普通路由
- 2.2 命名路由
- 3. 示例代码
- 4. 内容总结
我们在上一章回中介绍了"使用get显示Dialog"相关的内容,本章回中将介绍使用get进行路由管理.闲话休提,让我们一起Talk Flutter吧。

1. 概念介绍
我们在本章回中介绍的路由管理主要是指页面之间的跳转,该功能是Get包的主要功能之一,不过原生SDK中也提供了该功能。我们在前面章回中介绍Get包时提到过路
由管理功能,本章回中将详细介绍该功能的用法,同时也会和原生SDK中的功能做比较。
2. 使用方法
我们在本章回中介绍的路由管理功能主要包含普通路由管理和命名路由管理两个功能。我们将分不同的小节来介绍它们。
2.1 普通路由
我们在这里说的普通路由是指在路由中直接使用页面类对象,比如下面的代码中直接使用了YourPage这个对象,它代表项目中的某个页面。
Get.to(const YourPage());Navigator.of(context).push(MaterialPageRoute(builder: (context) => const YourPage()));
原生SDK中通过Navigator类来实现路由管理,该类提供了push,pop,push,pushReplacement等方法来实现路由跳转功能。Get包对此类进行了封装,它提供了相
关的方法来实现路由跳转功能,包中常用的方法如下:
- to():用来从当前页面跳转到参数是指定的页面,与原生中的push方法功能相同;
- back():用来从当前页面返回到上一级页面,与原生中的pop方法功能相同;
- off():用来从当前页面跳转到参数是指定的页面,并且取消下一个页面的导航(返回箭头),与原生中的pushReplacement方法功能相同;
- offAll():用来从当前页面跳转到参数指定的页面,并且删除所的有路由,与原生中的pushAndRemoveUntil方法功能相同;
上面介绍的这些方法使用十分方便,主要体现在两个方面:通过包名就可以直接调用;只需要在参数中传入跳转的页面就可以,不需要BuildContext对象;
2.2 命名路由
命名路由就是给页面起一个别名,在页面跳转时通过别名来跳转到指定的页面。它的用法详细如下:
- 给页面创建别名,并且把别名赋值给GetMaterialApp组件的getPages属性;
- 在GetMaterialApp组件的initialRoute属性中指定根路由;
- 使用包中的toNamed方法跳转到指定页面,该方法的的参数是页面的别名;
掌握上面介绍的使用步骤就可以调用包中的方法来使用命名路由,下面是包中提供的相关方法: - toNamed():用来从当前页面跳转到参数是指定的页面,与原生中的push方法功能相同;
- offNamed():用来从当前页面跳转到参数是指定的页面,并且取消下一个页面的导航(返回箭头),与原生中的pushReplacement方法功能相同;
- offAllNamed():用来从当前页面跳转到参数指定的页面,并且删除所的有路由,与原生中的pushAndRemoveUntil方法功能相同;
上面介绍的这些方法使用十分方便,主要体现在两个方面:通过包名就可以直接调用;只需要在参数中传入跳转的页面就可以,不需要BuildContext对象;此外,包中
还提供了其它的命名路由方法,大家可以去查看接口相关的代码。
3. 示例代码
GetMaterialApp(// home: GetHomePage(),///配置好路由后可以使用命名路由,配置方法和Material方法相同initialRoute: '/',getPages: [GetPage(name: '/', page: () => const GetHomePage(),),GetPage(name: '/overlay', page: () => const ExOverlayEntry(),),GetPage(name: '/html', page: () => const ExHtmlView(),),],
);ElevatedButton(onPressed: (){Get.toNamed('/html');// Navigator.of(context).pushNamed('/html');},child: const Text("Named"),),
上面的示例代码完全按照上一小节中的实现方法来编写,同时把包中路由方法赋值给了按钮的onPressed属性,这样在点击按钮时就可以跳转到其它的页面。这里只演示
了一种命名路由方法,其它的方法用法相同,大家可以自己动手去实践。
4. 内容总结
最后,我们对本章回的内容做一个全面的总结:
- Get提供了两种方法管理路由:普通路由和命名路由;
- 普通路由通过to,back,off()等方法来实现路由管理;
- 命名路由通过toNamed,offNamed(),offAllNamed()等方法来实现路由管理;
- Get包中进行路由管理的方法都是静态方法,并且不需要提供Context对象,使用十分方便;
看官们,与"使用get进行路由管理"相关的内容就介绍到这里,欢迎大家在评论区交流与讨论!
相关文章:

第五百零三回
文章目录 1. 概念介绍2. 使用方法2.1 普通路由2.2 命名路由 3. 示例代码4. 内容总结 我们在上一章回中介绍了"使用get显示Dialog"相关的内容,本章回中将介绍使用get进行路由管理.闲话休提,让我们一起Talk Flutter吧。 1. 概念介绍 我们在本章…...
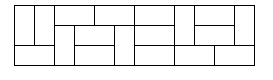
[动态规划] 完美覆盖
描述 一张普通的国际象棋棋盘,它被分成 8 乘 8 (8 行 8 列) 的 64 个方格。设有形状一样的多米诺牌,每张牌恰好覆盖棋盘上相邻的两个方格,即一张多米诺牌是一张 1 行 2 列或者 2 行 1 列的牌。那么,是否能够把 32 张多米诺牌摆放…...
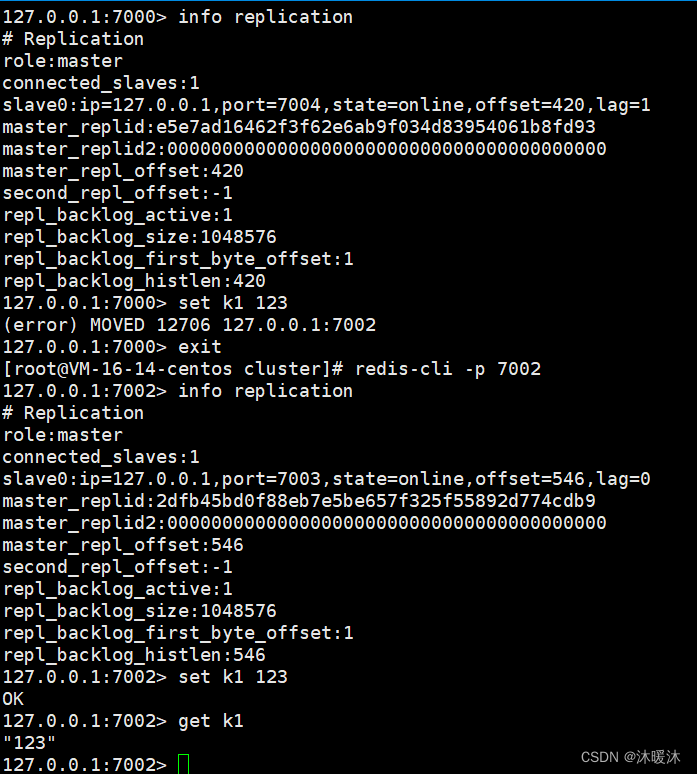
redis深入理解之实战
1、SpringBoot整合redis 1.1 导入相关依赖 <dependency><groupId>redis.clients</groupId><artifactId>jedis</artifactId> </dependency> <dependency><groupId>org.springframework.boot</groupId><artifactId&g…...

python设计模式---工厂模式
定义了一个抽象类Animal,并且让具体的动物类(Dog、Cat、Duck)继承自它,并实现了speak方法。然后创建了AnimalFactory工厂类,根据传入的参数来决定创建哪种动物的实例。 from abc import abstractmethod, ABCclass Anim…...

探索Vue 3.0中的v-html指令
探索Vue 3.0中的v-html指令 一、什么是v-html指令?1、 在Vue 3.0中使用v-html2、 注意事项 二、结语 一、什么是v-html指令? Vue.js作为一款流行的JavaScript框架,不断地演进着。随着Vue 3.0的发布,开发者们迎来了更加强大和灵活…...

anaconda 环境配置
官方网站下载地址: https://www.anaconda.com/download/ 国内清华镜像下载地址: https://mirrors.tuna.tsinghua.edu.cn/anaconda/archive/ 配置国内环境: conda config --add channels https://mirrors.tuna.tsinghua.edu.cn/anaconda/pkgs/free/ …...

DS:顺序表、单链表的相关OJ题训练(2)
欢迎各位来到 Harper.Lee 的学习世界! 博主主页传送门:Harper.Lee的博客主页 想要一起进步的uu欢迎来后台找我哦! 一、力扣--141. 环形链表 题目描述:给你一个链表的头节点 head ,判断链表中是否有环。如果链表中有某个…...
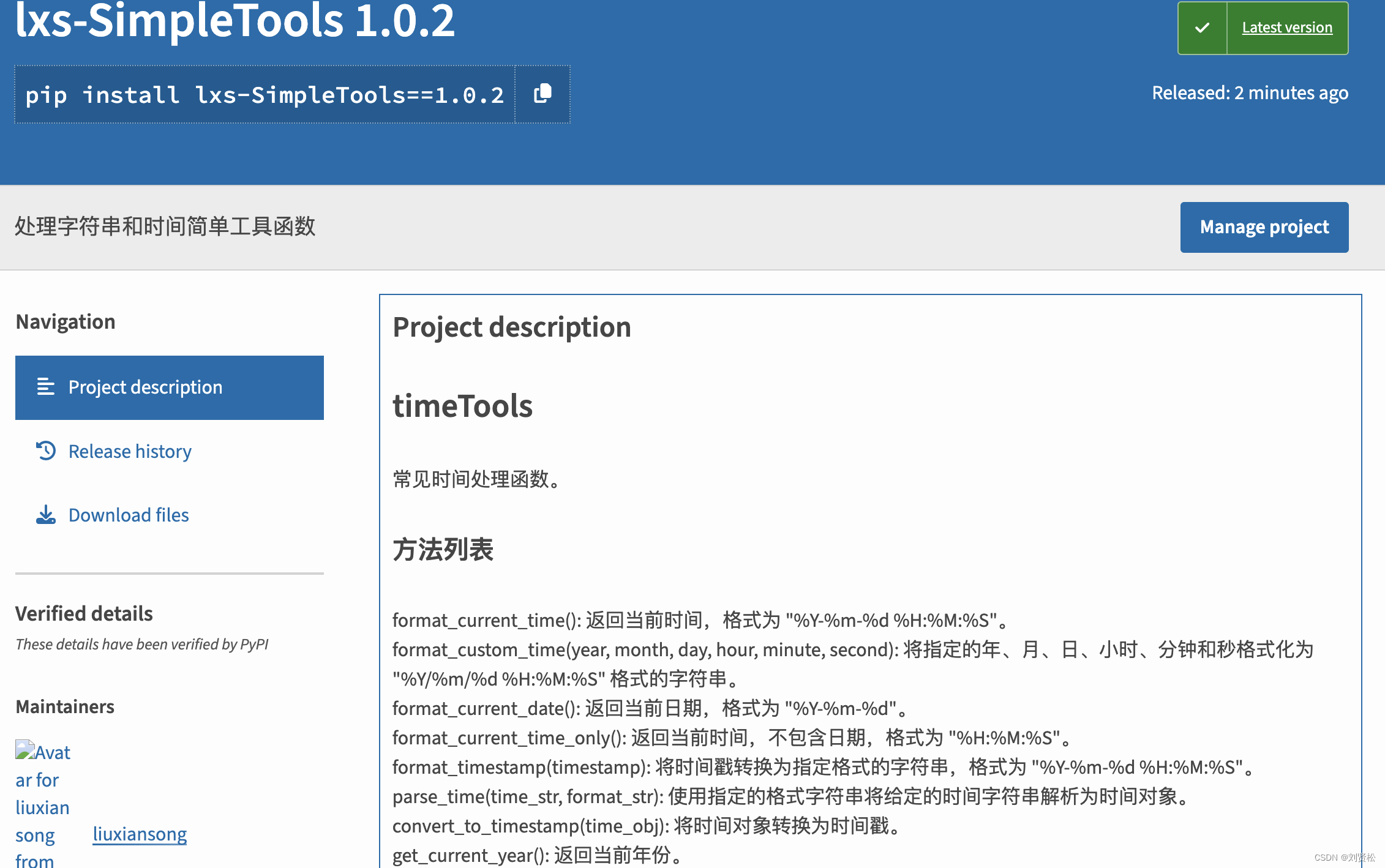
上传到 PyPI
将软件包上传到 PyPI(Python Package Index),您需要遵循以下步骤: 准备软件包:确保您的软件包满足以下要求: 包含一个 setup.py 文件,用于描述软件包的元数据和依赖项。包含软件包的源代码和必要…...
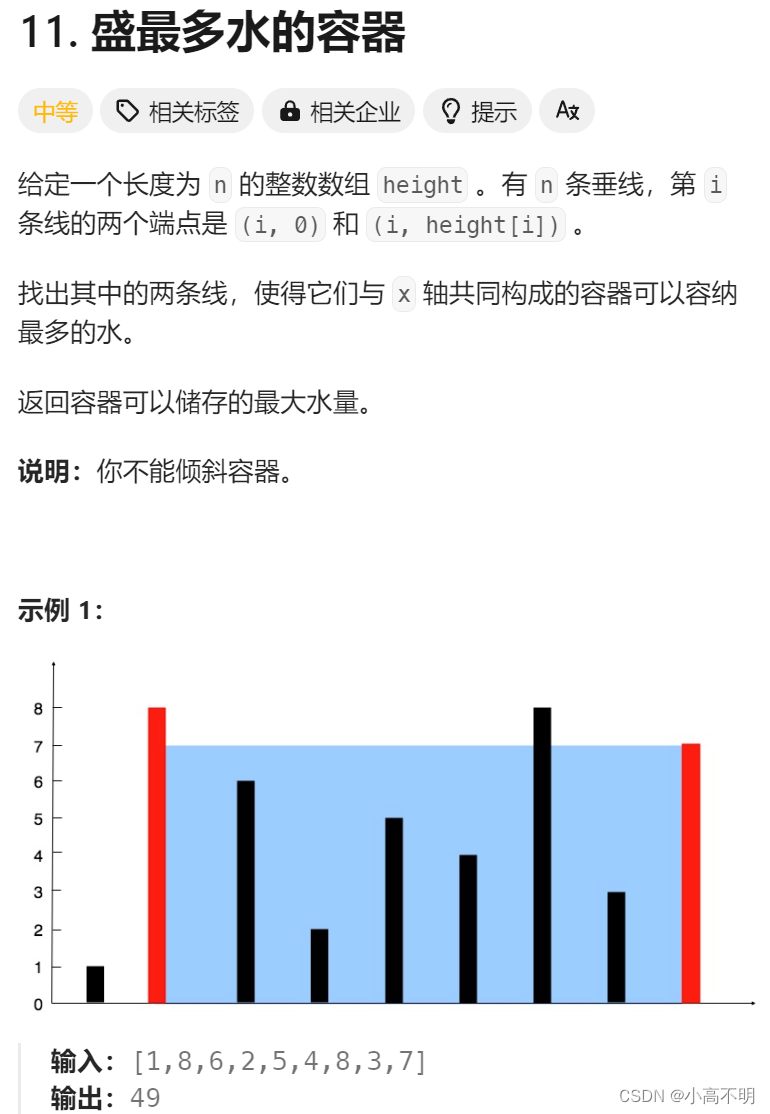
盛最多水的容器(双指针)
解题思路: 1,暴力解法(超时) 我们可以使用两层for循环进行遍历。找到那个最大的面积即可,这里我就不写代码了,因为写了也是超时。 2,双指针法 先定义两个指针一个在最左端,一个在…...
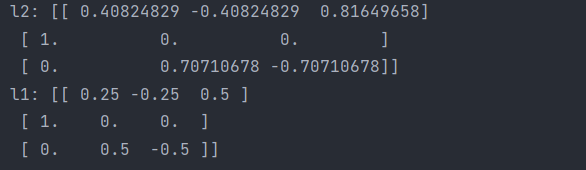
【深度学习】实验3 特征处理
特征处理 python 版本 3.7 scikit-learn 版本 1.0.2 1.标准化 from sklearn.preprocessing import StandardScaler from sklearn.preprocessing import MinMaxScaler from matplotlib import gridspec import numpy as np import matplotlib.pyplot as plt cps np.random.…...
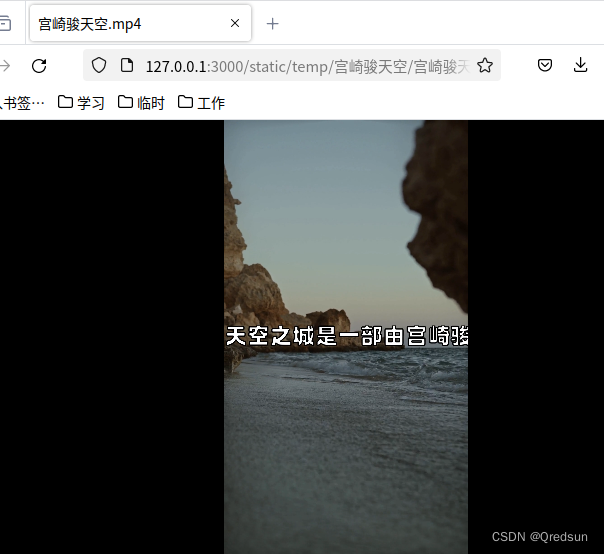
MoneyPrinter国内版改造
背景: MoneyPrinter 是一个自动生成短视频的开源项目。只需要输入短视频主题,然后就可以生成视频。 在国内环境运行时,框架中使用的youtube、抖音文字转语音等功能无法使用,需要对框架进行国内版改造,使其使用国内网络…...

C++ 派生类的引入与特性
一 继承与派生 从上面的例子可以看出: 继承:一旦指定了某种事物父代的本质特征,那么它的子代将会自动具有哪些性质。这就是一种朴素的可重用的概念。 派生:而且子代可以拥有父代没有的特性,这是可扩充的概念。 1 C 的…...
Poe是什么?怎样订阅Poe?
Poe(全称“开放探索平台”,Platform for Open Exploration)是一款由Quora开发的移动应用程序,于2022年12月推出。该应用程序内置建基于AI技术的聊天机器人,可供用户向机器人询问专业知识、食谱、日常生活,甚…...

基于FPGA的视频矩阵切换方案
一、单个显示设备的系统方案:会议室只有1个显示设备 会议室的信号源有很多,但是显示设备只有1个,这个时候最佳方案是使用切换器。 (1)切换器(控制方式:遥控器、软件、机箱面板、中控ÿ…...

.NET周刊【5月第1期 2024-05-05】
国内文章 一个开源轻量级的C#代码格式化工具(支持VS和VS Code) https://www.cnblogs.com/Can-daydayup/p/18164905 CSharpier是一个开源、免费的C#代码格式化工具,特点是轻量级且依赖Roslyn引擎重构代码格式。支持的IDE包括Visual Studio …...
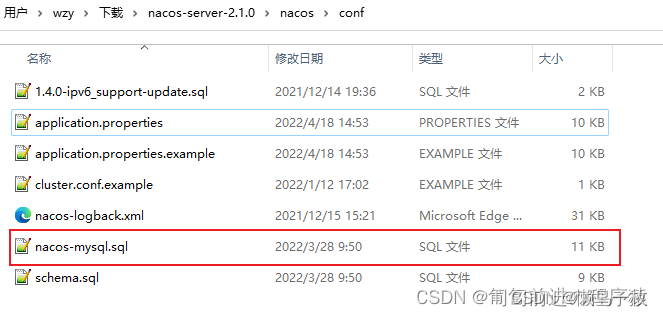
springcloud -nacos实战
一、nacos 功能简介 1.1.什么是Nacos? 官方简介:一个更易于构建云原生应用的动态服务发现(Nacos Discovery )、服务配置(Nacos Config)和服务管理平台。 Nacos的关键特性包括: 服务发现和服务健康监测动态配置服务动态DNS服务服务及其元数…...

第十五章 数据管理成熟度评估练习
单选题 (每题1分,共19道题) 1、 [单选] 下列选项中属于数据管理成熟度2级特征的选项是? A:很少或没有治理;有限的工具集;单个竖井(系统)内定义角色;控件(如果有的话的应用完全不一致);未解决的数据质量问题 B:治理开始出现;引入一致的工具集;定义了一些角色和…...

tcpdump速查表
tcpdump 速查表 -D 列出网络设备 ~]$ sudo tcpdump -D1.eth02.nflog (Linux netfilter log (NFLOG) interface)3.nfqueue (Linux netfilter queue (NFQUEUE) interface)4.any (Pseudo-device that captures on all interfaces)5.lo [Loopback]-i 指定网卡 前面列出的设备可以…...

单元测试与集成测试:软件质量的双重保障
目录 概述 单元测试 集成测试 单元测试的方法 白盒测试 黑盒测试 白盒测试的方法和用例设计 代码审查 集成测试 单元测试工具 结语 在软件开发中,测试是一个不可或缺的环节,它能够帮助我们发现和修复缺陷,确保软件的质量和可靠性。…...
孙宇晨对话大公网:香港Web3政策友好环境示范意义重大
日前,全球知名华文媒体大公网发布《湾区web3大有可为》重磅系列报道。报道通过对中国香港与大湾区其他城市Web3政策、行业创新和生态建设等方面的梳理,以及对行业领袖和重要行业机构的走访,全面展现了在大湾区一体化发展的背景下,Web3等数字经济模式在该地区的长远发展潜力。 …...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

初探Service服务发现机制
1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能:服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

【Elasticsearch】Elasticsearch 在大数据生态圈的地位 实践经验
Elasticsearch 在大数据生态圈的地位 & 实践经验 1.Elasticsearch 的优势1.1 Elasticsearch 解决的核心问题1.1.1 传统方案的短板1.1.2 Elasticsearch 的解决方案 1.2 与大数据组件的对比优势1.3 关键优势技术支撑1.4 Elasticsearch 的竞品1.4.1 全文搜索领域1.4.2 日志分析…...

WEB3全栈开发——面试专业技能点P7前端与链上集成
一、Next.js技术栈 ✅ 概念介绍 Next.js 是一个基于 React 的 服务端渲染(SSR)与静态网站生成(SSG) 框架,由 Vercel 开发。它简化了构建生产级 React 应用的过程,并内置了很多特性: ✅ 文件系…...

前端调试HTTP状态码
1xx(信息类状态码) 这类状态码表示临时响应,需要客户端继续处理请求。 100 Continue 服务器已收到请求的初始部分,客户端应继续发送剩余部分。 2xx(成功类状态码) 表示请求已成功被服务器接收、理解并处…...

boost::filesystem::path文件路径使用详解和示例
boost::filesystem::path 是 Boost 库中用于跨平台操作文件路径的类,封装了路径的拼接、分割、提取、判断等常用功能。下面是对它的使用详解,包括常用接口与完整示例。 1. 引入头文件与命名空间 #include <boost/filesystem.hpp> namespace fs b…...

Faiss vs Milvus 深度对比:向量数据库技术选型指南
Faiss vs Milvus 深度对比:向量数据库技术选型指南 引言:向量数据库的时代抉择 在AI应用爆发的今天,企业和开发者面临着如何存储和检索海量向量数据的重大技术选择。作为当前最受关注的两大解决方案,Faiss和Milvus代表了两种不同…...
