B树与B+树的奥秘:原理解析与性能
引言
B树和B+树是计算机科学中两个重要的数据结构,它们在数据库和文件系统中扮演着至关重要的角色。在处理大量数据时,高效的数据组织和检索方式是至关重要的,而B树和B+树正是为此而设计的。
B树和B+树都是多路查找树的变体,它们通过将多个键值存储在一个节点中,有效地减少了磁盘I/O访问次数,从而提高了数据检索的效率。这种优化对于处理大型数据库和文件系统特别重要,因为它们可以大大减少磁盘访问次数,提高了数据的读取和写入速度。
在本文中,我们将深入探讨B树和B+树的原理、操作以及它们之间的区别。首先,我们将介绍树结构的基础概念,包括二叉树、平衡树和多路查找树。然后,我们将详细讨论B树和B+树的定义、性质和节点结构,以及它们的构建过程、查找过程和删除过程。
接着,我们将比较B树和B+树在结构上的差异和性能上的差异,包括查找效率、插入和删除效率、磁盘读写性能以及范围查询的性能。我们还将探讨B树和B+树在不同场景下的适用性,并提供选择索引结构的依据。
通过分析一些著名数据库系统中B树和B+树的实际应用案例,我们将进一步理解它们在现实世界中的应用和优劣势。最后,我们将总结B树和B+树的主要特点,强调它们在现代计算机系统中的重要性,并指出它们的优缺点。
本文将帮助读者深入了解B树和B+树的奥秘,以及它们在数据库和文件系统中的应用。通过清晰的解释和丰富的内容,读者将能够更好地理解这两种重要的数据结构,并在实际应用中做出更明智的选择。
基础概念
树结构简介
二叉树
二叉树是一种常见的树结构,每个节点最多有两个子节点,分别称为左子节点和右子节点。这种结构方便了对数据的快速查找和排序操作。
平衡树
平衡树是一种特殊的二叉树,它的左右子树的高度差不超过1。通过保持树的平衡,平衡树能够确保在最坏情况下的查找效率仍然很高,避免了出现退化为链表的情况。
多路查找树
多路查找树是指每个节点可以包含多个子节点的树结构。相比于二叉树,多路查找树能够在每个节点存储更多的数据,提高了存储和检索的效率。
B树定义
B树的概念
B树是一种多路平衡查找树,它的每个节点可以含有多个子节点,且每个节点中的数据按顺序排列。B树通常应用于文件系统和数据库中,能够有效地支持范围查找和大数据量的存储。
B树的性质
- 所有叶子节点位于同一层级。
- 每个节点包含的关键字数量有上下界限。
- 根节点至少包含一个关键字。
- 非叶子节点的关键字按非降序排列。
B树的节点结构
B树的节点包含两种类型:内部节点和叶子节点。内部节点存储关键字和子节点指针,而叶子节点存储关键字和相关数据。
B+树定义
B+树的概念
B+树也是一种多路平衡查找树,与B树相比,B+树的叶子节点形成了一个有序链表,能够更快地支持范围查找操作。
B+树的性质
- 所有叶子节点通过指针连接成一个有序链表。
- 非叶子节点只存储索引,不存储数据。
- 叶子节点存储了全部数据,并且按顺序排列。
B+树的节点结构
B+树的节点结构与B树类似,但是在B+树中,叶子节点包含了全部数据,而内部节点仅包含索引。
这些基础概念是理解B树与B+树的重要前提,后续我们将深入探讨它们的构建过程、查找过程、删除过程以及在不同场景下的应用和性能比较。
B树的原理与操作
构建过程
节点分裂
B树的构建过程中,当一个节点已满时,需要进行节点分裂操作。节点分裂的基本思想是将一个节点中的关键字按中值分成两部分,并将中值提升到父节点中。这样可以保持B树的平衡性质。
节点分裂的具体步骤如下:
- 找到满节点中的中值。
- 将中值提升到父节点,并创建一个新的节点作为原节点的兄弟节点。
- 将原节点中较小的一部分关键字移动到新节点中,并更新节点的指针。
节点分裂操作的目的是保持B树的平衡,确保每个节点的关键字数量在一个合理的范围内,同时保持树的高度平衡。
键值插入
在B树中插入新的键值时,需要遵循以下步骤:
- 从根节点开始,按照关键字的大小顺序逐级向下查找合适的位置。
- 如果目标节点未满,则直接将键值插入到该节点中,并保持节点的关键字有序。
- 如果目标节点已满,则进行节点分裂操作,然后继续插入。
键值插入操作保证了B树的平衡性和有序性,使得数据的插入操作具有较好的性能。
查找过程
查找算法描述
B树的查找算法类似于二叉查找树,但由于B树的节点含有多个关键字,因此查找过程稍微复杂一些。查找算法描述如下:
- 从根节点开始,比较目标值与节点中的关键字,选择合适的子节点继续查找。
- 如果目标值小于当前节点中的最小关键字,则向左子节点查找;如果目标值大于当前节点中的最大关键字,则向右子节点查找。
- 重复以上步骤,直到找到目标值或者到达叶子节点为止。
B树的查找算法保证了在平衡树结构中高效地查找目标值,时间复杂度为O(log n)。
删除过程
节点合并
B树的删除操作可能导致节点的关键字数量低于最小要求,需要进行节点合并操作以保持树的平衡。节点合并的基本思想是将两个相邻节点合并成一个节点,并从父节点中删除相应的关键字。
节点合并的具体步骤如下:
- 找到待合并的两个相邻节点和它们的父节点。
- 将父节点中的一个关键字下移至合并后的节点中。
- 将另一个节点中的所有关键字移动至合并后的节点中。
- 更新父节点的指针,删除一个子节点指针。
节点合并操作的目的是减少树的高度,保持B树的平衡性质,同时避免了节点数量过多的情况。
键值删除
B树的键值删除操作涉及节点的合并和关键字的移动,具体步骤如下:
- 找到待删除的关键字所在的节点。
- 如果目标节点是叶子节点,则直接删除关键字。
- 如果目标节点是内部节点,则选择一个合适的后继关键字替换被删除的关键字,然后递归删除后继关键字。
键值删除操作保证了B树的平衡性和有序性,使得数据的删除操作也具有较好的性能。
这些原理和操作使得B树成为了一种在数据库和文件系统中广泛应用的高效数据结构。
B+树的原理与操作
构建过程
节点分裂
B+树的构建过程中,与B树相似,当一个节点已满时,也需要进行节点分裂操作。节点分裂的目的是保持B+树的平衡性和有序性,同时利用B+树叶子节点的链表结构提高范围查询的效率。
节点分裂的步骤如下:
- 找到满节点中的中值。
- 将中值提升到父节点中,并创建一个新的节点作为原节点的兄弟节点。
- 将原节点中较大的一部分关键字和相关数据移动到新节点中。
- 更新父节点中的指针,确保指向正确的子节点。
B+树的节点分裂操作保证了树的平衡性和有序性,同时维护了叶子节点的链表结构。
键值插入
B+树的键值插入操作与B树类似,但有一点不同的是,新插入的键值总是被插入到叶子节点中,而不会出现内部节点中的情况。插入操作的具体步骤包括:
- 从根节点开始,按照关键字的大小顺序逐级向下查找合适的叶子节点。
- 如果目标叶子节点未满,则直接将键值插入到该节点中,并保持节点的关键字有序。
- 如果目标叶子节点已满,则进行节点分裂操作,然后继续插入。
键值插入操作保证了B+树的平衡性和有序性,同时利用了叶子节点的链表结构提高了范围查询的效率。
查找过程
查找算法描述
B+树的查找算法与B树类似,但是在B+树中,所有的数据都存储在叶子节点中,并且叶子节点通过指针连接成一个有序链表。查找过程如下:
- 从根节点开始,比较目标值与节点中的关键字,选择合适的子节点继续查找。
- 如果目标值小于当前节点中的最小关键字,则向左子节点查找;如果目标值大于当前节点中的最大关键字,则向右子节点查找。
- 重复以上步骤,直到找到目标值或者到达叶子节点为止。
- 如果到达叶子节点,则在叶子节点的链表中顺序查找目标值。
B+树的查找算法保证了在平衡树结构中高效地查找目标值,同时通过链表结构提高了范围查询的效率。
删除过程
节点合并
B+树的删除操作可能导致节点的关键字数量低于最小要求,需要进行节点合并操作以保持树的平衡。节点合并的步骤与B树相似,具体操作如下:
- 找到待合并的两个相邻节点和它们的父节点。
- 将父节点中的一个关键字下移至合并后的节点中。
- 将另一个节点中的所有关键字移动至合并后的节点中。
- 更新父节点的指针,删除一个子节点指针。
节点合并操作保持了B+树的平衡性和有序性,同时通过合并叶子节点的链表提高了范围查询的效率。
键值删除
B+树的键值删除操作涉及节点的合并和关键字的移动,具体步骤与B树相似,但只需删除叶子节点中的目标关键字即可。
键值删除操作保证了B+树的平衡性和有序性,同时维护了叶子节点的链表结构,使得删除操作具有较好的性能。
B+树通过节点分裂、键值插入、查找和删除等操作,以及叶子节点的链表结构,实现了高效的数据存储和检索功能。
B树与B+树的区别
结构上的差异
节点存储
-
B树:
- B树的每个节点既存储关键字,又存储对应的数据。
- 内部节点和叶子节点的结构相同,都可以存储数据。
- B树的节点通常更大,因为每个节点需要存储数据,这可能导致更多的磁盘I/O操作。
-
B+树:
- B+树的内部节点只存储关键字,不存储数据,只有叶子节点存储数据。
- 内部节点和叶子节点的结构不同,内部节点只存储索引。
- B+树的内部节点通常更小,因为不需要存储数据,这减少了磁盘I/O操作的次数。
键值分布
-
B树:
- B树的每个节点包含了一部分关键字和对应的数据,且按照大小顺序存储。
- 可以直接通过内部节点查找到对应的数据,而不需要在叶子节点中进行额外的查找操作。
-
B+树:
- B+树的内部节点仅包含了关键字,不包含数据,数据全部存储在叶子节点中。
- 内部节点的关键字范围与其子节点的范围完全对应,而叶子节点通过链表连接,使得范围查询更高效。
性能比较
查找效率
-
B树:
- 由于B树的节点中包含了部分数据,因此在查找过程中可以直接访问内部节点,减少了查找路径的长度,提高了查找效率。
-
B+树:
- B+树的内部节点仅包含了索引,查找过程需要沿着内部节点一直查找到叶子节点才能找到数据,因此在查找过程中可能需要更多的磁盘I/O操作。
插入和删除效率
-
B树:
- 插入和删除操作可能需要更新内部节点和叶子节点,但由于数据存储在内部节点中,所以这些操作相对较快。
-
B+树:
- 插入和删除操作只需要更新内部节点和叶子节点的关键字索引,因此这些操作通常更快,尤其是在大规模数据插入和删除时。
磁盘读写性能
-
B树:
- 由于B树的节点包含了数据,因此可能需要更多的磁盘I/O操作来读取或写入节点数据,导致性能略低于B+树。
-
B+树:
- B+树的内部节点只存储索引,叶子节点通过链表连接,减少了磁盘I/O操作的次数,因此具有更好的磁盘读写性能。
范围查询
-
B树:
- B树在进行范围查询时可能需要遍历多个节点来获取满足条件的数据,因为数据分散在各个节点中。
-
B+树:
- B+树在进行范围查询时只需要在叶子节点的链表上顺序查找,因此范围查询的效率更高。
综上所述,B树和B+树在结构上和性能上存在一些差异,具体的选择取决于应用场景和需求。通常来说,对于大规模数据存储和范围查询频繁的场景,B+树更适合;而对于需要频繁进行插入和删除操作的场景,B树可能更合适。
应用场景
B树的适用场景
-
文件系统:
- 在文件系统中,B树常用于索引文件的内容和目录结构,能够快速定位到文件块的位置,提高文件的访问速度。
-
数据库系统:
- 在数据库系统中,B树通常用于构建索引,加速数据库的查找、插入和删除操作。特别是在磁盘存储的情况下,B树的结构有利于减少磁盘I/O操作。
-
文件检索:
- B树可以用于构建搜索引擎的倒排索引,能够快速检索到包含特定关键字的文件或文档,应用于信息检索和全文检索系统中。
-
内存管理:
- 在操作系统中,B树可以用于管理虚拟内存和物理内存的分配和释放,以及页面置换算法的实现。
B+树的适用场景
-
数据库索引:
- B+树是数据库系统中常用的索引结构,特别适合用于范围查询和排序操作,提高了数据库查询的效率。
-
数据仓库:
- 在数据仓库中,B+树可以用于构建OLAP(联机分析处理)系统的多维索引,支持复杂的查询和分析操作。
-
文件存储:
- B+树可以用于构建文件系统的目录结构和索引,加速文件的查找和访问操作,尤其适用于大型文件存储系统。
-
地理信息系统:
- 在GIS(地理信息系统)中,B+树可以用于管理地理数据的空间索引,实现快速的地理空间查询和分析功能。
不同场景下的选择依据
-
数据访问模式:
- 如果系统主要进行范围查询和排序操作,B+树更适合;如果系统主要进行随机查找和频繁的插入、删除操作,B树可能更合适。
-
存储介质:
- 在磁盘存储的情况下,B+树通常具有更好的性能,因为其内部节点更小,减少了磁盘I/O操作的次数;而在内存存储的情况下,B树可能更适合,因为其节点包含了数据,减少了内存访问的次数。
-
查询需求:
- 如果系统需要支持范围查询、分页查询等复杂查询操作,B+树更适合;如果系统主要进行单个关键字的查找操作,B树可能更合适。
综上所述,选择B树还是B+树取决于具体的应用场景和需求,需要根据系统的数据特点、访问模式和性能要求进行权衡和选择。
实际案例分析
MySQL中的索引结构选择
MySQL数据库中使用了B树和B+树索引结构,具体选择取决于存储引擎和索引类型。
-
InnoDB引擎:
- InnoDB存储引擎使用B+树索引结构,这是默认的存储引擎。
- B+树索引适用于范围查询和排序操作,因此对于大多数应用场景都能够提供良好的性能。
-
MyISAM引擎:
- MyISAM存储引擎默认使用B树索引结构。
- B树索引在单点查询性能上可能略优于B+树,但在范围查询等场景下性能不及B+树。
Oracle中的索引结构选择
Oracle数据库中也支持多种索引类型,包括B树索引和B+树索引。
-
B树索引:
- Oracle数据库中的普通索引(Non-Unique Index)使用了B树索引结构。
- B树索引适用于单点查询,但在范围查询和排序操作上性能相对较低。
-
B+树索引:
- Oracle数据库中的唯一索引(Unique Index)和聚集索引(Clustered Index)使用了B+树索引结构。
- B+树索引在范围查询和排序操作上性能更好,适用于多种查询场景。
总体比较
-
MySQL与Oracle:
- MySQL和Oracle数据库都采用了B树和B+树索引结构,但默认的存储引擎和索引类型不同。
- MySQL的默认引擎InnoDB使用了B+树索引,而Oracle的普通索引采用了B树索引。
-
性能考量:
- 对于需要大量范围查询和排序操作的应用,B+树索引更适合;而对于单点查询较多的场景,B树索引可能更合适。
-
数据库优化:
- 在实际应用中,根据数据库的具体需求和性能瓶颈,可以针对性地选择适合的索引类型和存储引擎,进行数据库性能优化。
综上所述,MySQL和Oracle等数据库系统在选择B树和B+树索引结构时,需要根据具体的应用场景和性能需求进行选择,以实现最佳的数据库性能和效率。
总结
B树和B+树作为常见的索引结构,在数据库和文件系统中发挥着重要作用。它们各自具有一系列特点,针对不同的应用场景有着各自的优势和劣势。
B树的特点
- 节点存储:B树的内部节点和叶子节点都存储数据,适用于内存较小的情况。
- 键值分布:节点中的键值按顺序存储,适合单点查询操作。
- 性能表现:在单点查询时性能可能略优于B+树,但在范围查询等操作上性能较差。
- 适用场景:适合单点查询较多的情况,如文件系统的目录结构。
B+树的特点
- 节点存储:B+树的内部节点只存储键值信息,数据全部存储在叶子节点上,适合大规模数据存储。
- 键值分布:叶子节点之间通过链表相连,适合范围查询和排序操作。
- 性能表现:在范围查询、排序和插入删除等操作上性能较优。
- 适用场景:适合需要支持范围查询和排序操作的数据库系统。
总体评价
- B树适用于单点查询较多的场景,性能可能略优于B+树,但在范围查询和排序操作上性能不及B+树。
- B+树适用于需要支持范围查询和排序操作的场景,性能优于B树,尤其适合大规模数据存储。
综上所述,选择B树还是B+树取决于具体的应用需求和性能要求,需要根据系统的数据特点、访问模式和存储介质进行权衡和选择,以达到最佳的性能和效率。
参考文献
-
Cormen, T. H., Leiserson, C. E., Rivest, R. L., & Stein, C. (2009). Introduction to Algorithms (Third Edition). MIT Press.
-
Silberschatz, A., Korth, H. F., & Sudarshan, S. (2010). Database System Concepts. McGraw-Hill Education.
-
MySQL Documentation: https://dev.mysql.com/doc/
-
Oracle Documentation: https://docs.oracle.com/
-
Garcia-Molina, H., Ullman, J. D., & Widom, J. (2008). Database Systems: The Complete Book. Pearson.
-
Comer, D. (1979). The Ubiquitous B-Tree. ACM Computing Surveys (CSUR), 11(2), 121-137.
-
Lehman, P. L., & Yao, S. B. (1981). Efficient Locking for Concurrent Operations on B-Trees. ACM Transactions on Database Systems (TODS), 6(4), 650-670.
-
Bayer, R., & McCreight, E. M. (1972). Organization and Maintenance of Large Ordered Indexes. Acta Informatica, 1(3), 173-189.
-
Härder, T., & Reuter, A. (1983). Principles of Transaction-Oriented Database Recovery. Computing Surveys (CSUR), 15(4), 287-317.
-
Lewis, P. M., Bernstein, P. A., & Karger, D. R. (1980). An Efficient Algorithm for Concurrently Inserting and Deleting Keys in a B-tree. ACM Transactions on Database Systems (TODS), 5(3), 354-382.
相关文章:

B树与B+树的奥秘:原理解析与性能
引言 B树和B树是计算机科学中两个重要的数据结构,它们在数据库和文件系统中扮演着至关重要的角色。在处理大量数据时,高效的数据组织和检索方式是至关重要的,而B树和B树正是为此而设计的。 B树和B树都是多路查找树的变体,它们通…...

Unity组件入门篇目录
Audio AudioChorusFilter......................................点击导航AudioDistortionFilter..................................点击导航AudioEchoFilter.........................................点击导航AudioHighPassFilter..................................点击导…...

【Python技术】使用akshare、pandas高效复盘每日涨停板行业分析
作为一个程序员宝爸,每天的时间很宝贵,工作之余除了辅导孩子作业,就是补充睡眠。 怎么快速高效的进行当天A股涨停板的复盘,便于第二天的跟踪。这里简单写个示例, 获取当天连涨数排序,以及所属行业排序。 …...
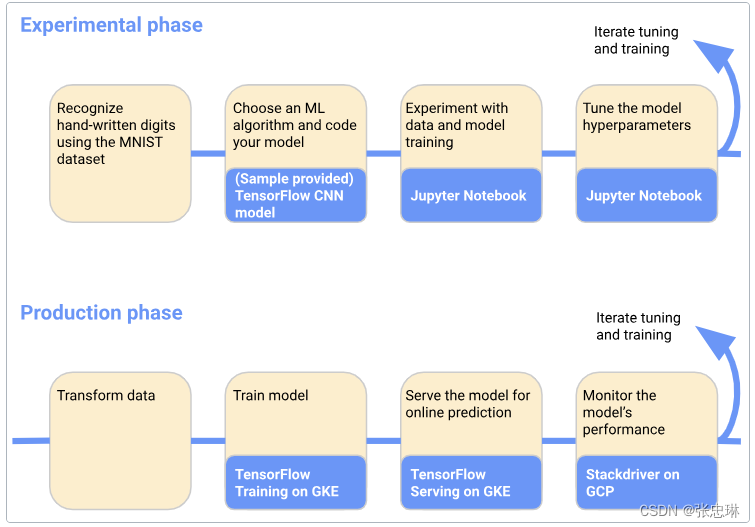
kubeflow文档-介绍与架构
1. kubeflow介绍 Kubeflow项目致力于使机器学习(ML)工作流在Kubernetes上的部署变得简单、可移植和可扩展。目标不是重新创建其他服务,而是提供一种直接的方法,将ML的开源系统部署到不同的基础设施中。无论在哪里运行Kubernetes&a…...

传输层的TCP流量控制比数据链路层作用范围更广
数据链路层的流量控制主要在相邻节点之间进行,它确保在单个链路或网络段上不会发生数据过载。例如,在以太网中,数据链路层使用停止-等待协议或滑动窗口机制来限制发送方发送的数据量,以避免接收方无法处理数据。 而传输层的 TCP 流…...

CSS表格
标准的表格结构 table标签:定义表格 caption标签:定义表格标题,这个标题会居中显示在表格上,一个表格只能定义一个标题 th标签:定义表格的表头,通常成粗体居中表示 tr标签:定义表格的一行 td标…...

东芝移动硬盘数据恢复方法有哪些
谁能懂我此刻的心情啊!移动硬盘用起来真的超级方便,如今我的工作几乎都离不开它,用来存放各种重要文件。可是,让人头疼的事情发生了,昨天我发现移动硬盘里的部分数据竟然莫名其妙地消失了!这可咋整啊&#…...

FullCalendar日历组件集成实战(1)
背景 有一些应用系统或应用功能,如日程管理、任务管理需要使用到日历组件。虽然Element Plus也提供了日历组件,但功能比较简单,用来做数据展现勉强可用。但如果需要进行复杂的数据展示,以及互动操作如通过点击添加事件࿰…...
wps
文章目录 取消自动升级、WPS热点及广告推送excel数字大小排序函数不起作用vlookup函数 取消自动升级、WPS热点及广告推送 打开WPS Office,点击左上角“首页”图标,依次点击右上角“设置”—>“配置和修复工具”。在弹出框点击“高级”,选…...
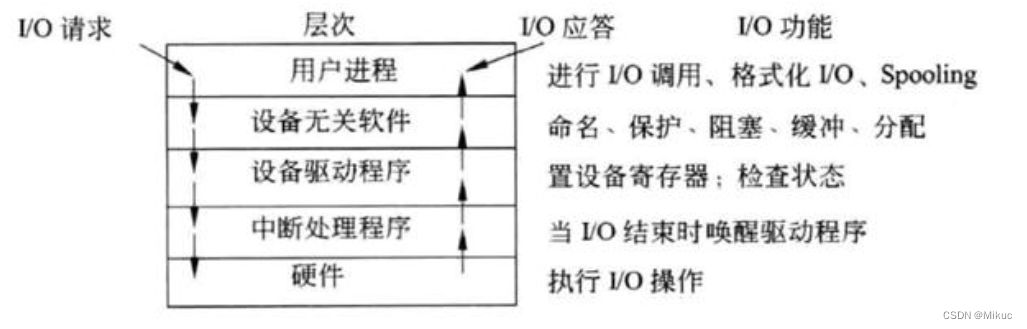
【软设】常见易错题汇总
目录 计算机系统基础 程序语言基础 数据结构 算法设计与分析 计算机网络与信息安全 软件工程基础 开发方法(结构化与面向对象) 数据库 操作系统 知识产权相关的法律法规 🤯🤯🤯🤯🤯ǹ…...

安全数据交换系统哪个好?该如何选型?
安全数据交换系统是用于在不同网络或组织之间安全、高效地传输和共享数据的解决方案。安全数据交换系统对于任何需要处理敏感数据、确保数据安全、并满足合规要求的组织来说都是至关重要的。 这种系统通常用于以下目的: 1)数据传输:允许用户…...
用matplotlib制作代码和色块
代码如下: # 声明 # -*- coding: utf-8 -*- """ Created on Mon May 13 11:18:59 2024author: sankang """ # 这里调用包 import matplotlib as mpl import matplotlib.pyplot as plt import numpy as npplt.rcParams[axes.unicode_…...

centos无法tab补全至文件
很奇怪的需求:redhat 7.9版本用cd 只能到目录,无法到文件 我个人认为不是个问题,但是甲方需求,你懂的 首先,我们要搞清楚tab补全功能的包bash-completion是否安装,这里肯定是安装了,不过还是看…...
: 训练设置)
大模型训练框架DeepSpeed使用入门(1): 训练设置
文章目录 一、安装二、训练设置Step1 第一步参数解析Step2 初始化后端Step3 训练初始化 三、训练代码展示 官方文档直接抄过来,留个笔记。 https://deepspeed.readthedocs.io/en/latest/initialize.html 使用案例来自: https://github.com/OvJat/DeepSp…...
自定义类型——结构体、枚举和联合
自定义类型——结构体、枚举和联合 结构体结构体的声明匿名结构体结构体的自引用结构体的初始化结构体的内存对齐修改默认对齐数结构体传参 位段枚举联合 结构体 结构是一些值的集合,这些值被称为成员变量,结构的每个成员可以是不同类型的变量。 数组是…...

Windows11系统安装Mysql8之后,启动服务net start mysql报错“服务没有响应控制功能”的解决办法
问题 系统环境:Windows11 数据库版本:Mysql8 双击安装,一路下一步,完成,很顺利,但是开启服务后 net start mysql 报错: 服务没有响应控制功能。 请键入 NET HELPMSG 2186 以获得更多的帮助 不…...

WIFI模块的AT指令联网数据交互--第十天
1.1.蓝牙,ESP-01s,Zigbee, NB-Iot等通信模块都是基于AT指令的设计 初始配置和验证 ESP-01s出厂波特率正常是115200, 注意:AT指令,控制类都要加回车,数据传输时不加回车 1.2.上电后,通过串口输出一串系统…...

设计模式Java实现-迭代器模式
✨这里是第七人格的博客✨小七,欢迎您的到来~✨ 🍅系列专栏:设计模式🍅 ✈️本篇内容: 迭代器模式✈️ 🍱 本篇收录完整代码地址:https://gitee.com/diqirenge/design-pattern 🍱 楔子 很久…...
单页源码加密屋zip文件加密API源码
简介: 单页源码加密屋zip文件加密API源码 api源码里面的参数已改好,往服务器或主机一丢就行,出现不能加密了就是加密次数达到上限了,告诉我在到后台修改加密次数 点击下载...

47.全排列
1.题目 47. 全排列 II - 力扣(LeetCode)https://leetcode.cn/problems/permutations-ii/description/ 2.思路 注意剪枝的条件 3.代码 class Solution {vector<int> path;vector<vector<int>> ret;bool check[9]; public:vector<…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...
