数学建模——线性回归模型

目录
1.线性回归模型的具体步骤和要点:
1.收集数据:
2.探索性数据分析:
3.选择模型:
4.拟合模型:
5.评估模型:
1.R平方(R-squared):
2.调整R平方(Adjusted R-squared):
3.残差分析:
4.方差膨胀因子(VIF):
6.解释结果:
7.预测与应用:
8.检验假设:
2.线性回归模型公式分析包括以下几个方面:
编辑
3.模型代码实现
1.代码_python
2.图形
1.线性回归模型的具体步骤和要点:
1.收集数据:
首先,需要收集与研究问题相关的数据。这些数据应包括一个或多个自变量(特征)和一个因变量(目标)。
2.探索性数据分析:
在建立模型之前,通常会对数据进行探索性分析,包括可视化和描述性统计分析,以了解数据的分布、相关性和异常值等情况。
3.选择模型:
根据问题的特点选择合适的线性回归模型。如果只有一个自变量,可以使用简单线性回归模型;如果有多个自变量,可以使用多元线性回归模型。
4.拟合模型:
利用最小二乘法或其他拟合方法来估计模型的参数。最小二乘法是一种常用的方法,它通过最小化观测值与模型预测值之间的残差平方和来确定参数。
5.评估模型:
评估模型的好坏以及对数据的拟合程度。常用的评估指标包括R平方、调整R平方、均方误差等。
1.R平方(R-squared):
R平方是一个衡量模型拟合优度的指标,表示因变量的变异中能被自变量解释的比例。R平方越接近1,说明模型对数据的拟合越好。
2.调整R平方(Adjusted R-squared):
调整R平方考虑了自变量的数量和样本量,相比于R平方更可靠。
3.残差分析:
分析残差是否呈现出随机分布,检查是否满足模型假设。
4.方差膨胀因子(VIF):
用于检测自变量之间的多重共线性问题。
6.解释结果:
分析模型的参数估计,理解自变量与因变量之间的关系。通过检查参数的符号和大小,可以了解自变量对因变量的影响方向和程度。
7.预测与应用:
利用拟合好的模型进行预测或者应用。可以使用模型对新的数据进行预测,也可以利用模型进行决策支持或政策制定等。
8.检验假设:
在应用模型时,需要检验模型的假设是否成立,例如线性关系、常数方差、独立误差等。如果假设不成立,可能需要对模型进行修正或者选择其他的建模方法。
2.线性回归模型公式分析包括以下几个方面:
3.模型代码实现
具体的需要根据具体数据磨合
1.代码_python
import numpy as np
import statsmodels.api as sm
import matplotlib.pyplot as plt# 准备数据
np.random.seed(0)
X = np.random.rand(100, 2) # 两个自变量
y = 2 * X[:,0] + 3 * X[:,1] + np.random.randn(100) # 因变量# 添加常数项
X = sm.add_constant(X)# 拟合线性回归模型
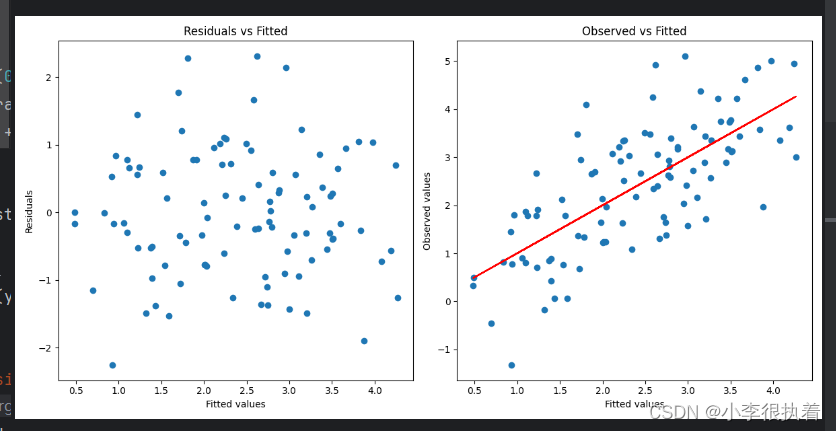
model = sm.OLS(y, X).fit()# 绘制残差图
plt.figure(figsize=(12, 6))
plt.subplot(1, 2, 1)
plt.scatter(model.fittedvalues, model.resid)
plt.xlabel('Fitted values')
plt.ylabel('Residuals')
plt.title('Residuals vs Fitted')# 绘制预测值与观测值的散点图
plt.subplot(1, 2, 2)
plt.scatter(model.fittedvalues, y)
plt.xlabel('Fitted values')
plt.ylabel('Observed values')
plt.title('Observed vs Fitted')# 添加拟合直线
plt.plot(model.fittedvalues, model.fittedvalues, color='red')plt.tight_layout()
plt.show()# 绘制参数估计的置信区间
plt.figure(figsize=(8, 6))
model_params = model.params
conf_int = model.conf_int()
plt.errorbar(model_params.index, model_params, yerr=model_params - conf_int[:, 0], fmt='o')
plt.axhline(0, color='red', linestyle='--')
plt.xlabel('Parameters')
plt.ylabel('Estimate')
plt.title('Parameter Estimates with Confidence Intervals')
plt.xticks(rotation=45)
plt.show()2.图形
相关文章:

数学建模——线性回归模型
目录 1.线性回归模型的具体步骤和要点: 1.收集数据: 2.探索性数据分析: 3.选择模型: 4.拟合模型: 5.评估模型: 1.R平方(R-squared): 2.调整R平方(Ad…...

景源畅信:抖音小店比较冷门的品类分享?
在抖音小店的世界里,热门品类总是吸引着众多商家和消费者的目光。然而,就像星空中的繁星,虽不那么耀眼却依然存在的冷门品类同样值得我们关注。它们或许不似服装、美妆那样日进斗金,但正是这些小众市场的存在,为平台带…...

java项目之企业资产管理系统(springboot+vue+mysql)
风定落花生,歌声逐流水,大家好我是风歌,混迹在java圈的辛苦码农。今天要和大家聊的是一款基于springboot的企业资产管理系统。项目源码以及部署相关请联系风歌,文末附上联系信息 。 项目简介: 管理员功能有个人中心&…...

[ardunio ide导入blinker库]
1 blinker库下载地址 https://github.com/blinker-iot/blinker-library2 导入方法一 zip导入 项目 -> 导入库 ->添加.zip库 3 导入方法二...

Llama 3 超级课堂 -笔记
课程文档: https://github.com/SmartFlowAI/Llama3-Tutorial 课程视频:https://space.bilibili.com/3546636263360696/channel/series 1 环境配置 1.1 创建虚拟环境,名为:llama3 conda create -n llama3 python3.10 1.2 下载、安装 pyt…...

Leetcode 第 129 场双周赛题解
Leetcode 第 129 场双周赛题解 Leetcode 第 129 场双周赛题解题目1:3127. 构造相同颜色的正方形思路代码复杂度分析 题目2:3128. 直角三角形思路代码复杂度分析 题目3:3129. 找出所有稳定的二进制数组 I思路代码复杂度分析 题目4:…...
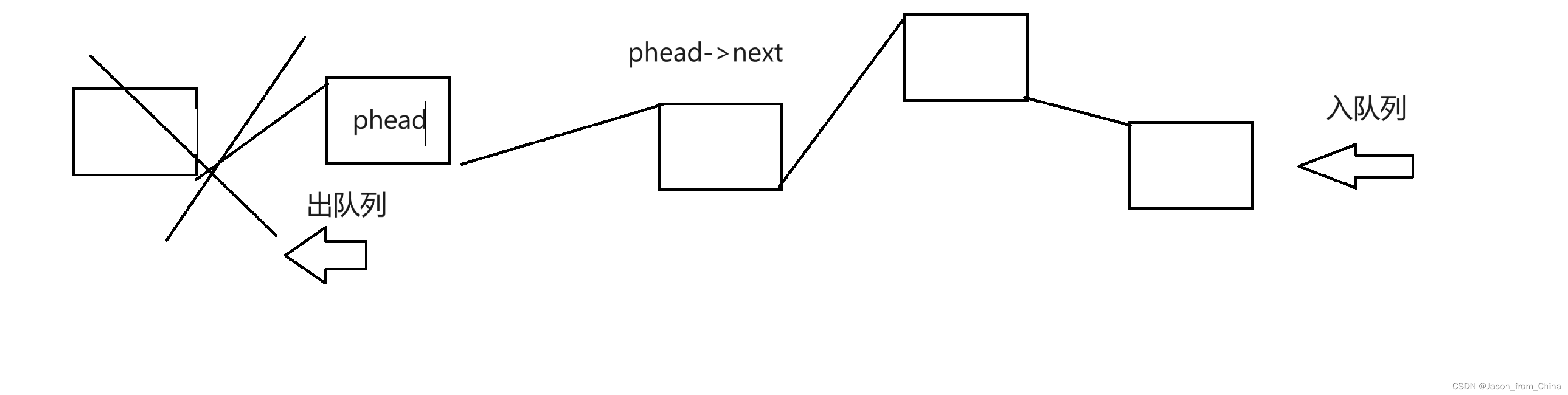
队列的讲解
队列的概念 队列:只允许在一端进行插入数据操作,在另一端进行删除数据操作的特殊线性表,队列具有先进先出FIFO(First In First Out) 入队列:进行插入操作的一端称为队尾 出队列:进行删除操作的一端称为队头 一端进另一端出 也就是可以做到,先…...
)
算法学习笔记(LCA)
L C A LCA LCA:树上两个点的最近公共祖先。(两个节点所有公共祖先中,深度最大的公共祖先) L C A LCA LCA的性质: 在所有公共祖先中, L C A ( x , y ) LCA(x,y) LCA(x,y)到 x x x和 y y y的距离都最短。 x …...

记一次苹果appstore提审拒审问题1.2
有关苹果appstore审核1.2问题的处理方案 2023.8.6苹果回复 Bug Fix Submissions The issues weve identified below are eligible to be resolved on your next update. If this submission includes bug fixes and youd like to have it approved at this time, reply to thi…...
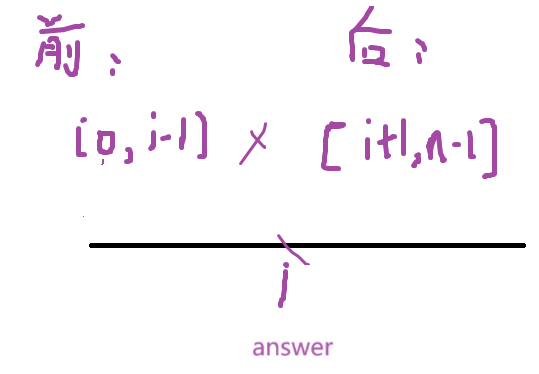
在做题中学习(59):除自身以为数组的乘积
238. 除自身以外数组的乘积 - 力扣(LeetCode) 解法:前缀积和后缀积 思路:answer中的每一个元素都是除自己以外所有元素的和。那就处理一个前缀积数组和后缀积数组。 而前缀积(f[i])是:[0,i-1]所有元素的乘积 后缀…...

centos 把nginx更新到最新版本
yum install epel-release # 添加 EPEL 软件仓库,这是 Nginx 官方软件仓库的依赖项 yum install yum-utils # yum-utils 包含了 yum-config-manager 工具,它可以让您轻松地启用、禁用或配置 yum 软件仓库 vi /etc/yum.repos.d/nginx.repo # 增加以下内容…...
01.认识HTML及常用标签
目录 URL(统一资源定位系统) HTML(超文本标记语言) 1)html标签 2)head标签 3)title标签 4)body标签 标签的分类 DTD文档声明 基础标签 1)H系列标签 2)…...

从零开始:C++ String类的模拟实现
文章目录 引言1.类的基本结构2.构造函数和析构函数3.基本成员函数总结 引言 在C编程中,字符串操作是非常常见且重要的任务。标准库中的std::string类提供了丰富且强大的功能,使得字符串处理变得相对简单。然而,对于学习C的开发者来说&#x…...
银河麒麟服务器操作系统V10-SP2部署gitlab服务
安装依赖 yum -y install python3-policycoreutils openssh-server openssh-clients postfix cronie curl下载gitlab-ce-15.4.2-ce.0.el8.x86_64.rpm安装包。 wget --content-disposition https://packages.gitlab.com/gitlab/gitlab-ce/packages/el/8/gitlab-ce-15.4.2-ce.0…...
【计算机毕业设计】基于SSM+Vue的线上旅行信息管理系统【源码+lw+部署文档+讲解】
目录 1 绪论 1.1 研究背景 1.2 设计原则 1.3 论文组织结构 2 系统关键技术 2.1JSP技术 2.2 JAVA技术 2.3 B/S结构 2.4 MYSQL数据库 3 系统分析 3.1 可行性分析 3.1.1 技术可行性 3.1.2 操作可行性 3.1.3 经济可行性 3.1.4 法律可行性 3.2系统功能分析 3.2.1管理员功能分析 3.2.…...

链表CPP简单示例
链表创建 链表打印全部内容 获取链表长度 链表根据指定位置添加元素 链表根据指定位置删除元素 #include <iostream> using namespace std;// 1、创建结构体// typedef 经常在结构中使用 typedef 别名 typedef struct node {int date;struct node* next; // 必须要自己…...

智能EDM邮件群发工具哪个好?
企业之间的竞争日益激烈,如何高效、精准地触达目标客户,成为每个市场战略家必须面对的挑战。在此背景下,云衔科技凭借其前沿的AI技术和深厚的行业洞察,匠心推出了全方位一站式智能EDM邮件营销服务平台,重新定义了邮件营…...

低代码与AI技术发展:开启数字化新时代
随着数字化转型的深入推进,低代码和AI技术逐渐成为各行各业关注的焦点。这两种技术的发展不仅改变了传统开发模式,还为企业创新和产业升级提供了新契机。本文将探讨这两种技术在实际应用中的相互促进作用,以及它们为我国经济社会发展带来的机…...

风电功率预测 | 基于遗传算法优化BP神经网络实现风电功率预测(附matlab完整源码)
风电功率预测 风电功率预测 | 基于遗传算法优化BP神经网络实现风电功率预测(附matlab完整源码)完整代码风电功率预测 | 基于遗传算法优化BP神经网络实现风电功率预测(附matlab完整源码) 基于遗传算法优化BP神经网络是一种常见的方法,用于改进BP神经网络在风电功率预测中的性…...

uni-segmented-control插件使用
dcloud插件市场 前端/uniapp 1.HBuildX打开目标项目 2.进入dcloud插件市场下载目标插件 3.看到如下提示(已经可以在目标项目中使用插件啦) 4.项目正式使用...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

Python+ZeroMQ实战:智能车辆状态监控与模拟模式自动切换
目录 关键点 技术实现1 技术实现2 摘要: 本文将介绍如何利用Python和ZeroMQ消息队列构建一个智能车辆状态监控系统。系统能够根据时间策略自动切换驾驶模式(自动驾驶、人工驾驶、远程驾驶、主动安全),并通过实时消息推送更新车…...

永磁同步电机无速度算法--基于卡尔曼滤波器的滑模观测器
一、原理介绍 传统滑模观测器采用如下结构: 传统SMO中LPF会带来相位延迟和幅值衰减,并且需要额外的相位补偿。 采用扩展卡尔曼滤波器代替常用低通滤波器(LPF),可以去除高次谐波,并且不用相位补偿就可以获得一个误差较小的转子位…...
的打车小程序)
基于鸿蒙(HarmonyOS5)的打车小程序
1. 开发环境准备 安装DevEco Studio (鸿蒙官方IDE)配置HarmonyOS SDK申请开发者账号和必要的API密钥 2. 项目结构设计 ├── entry │ ├── src │ │ ├── main │ │ │ ├── ets │ │ │ │ ├── pages │ │ │ │ │ ├── H…...

Yii2项目自动向GitLab上报Bug
Yii2 项目自动上报Bug 原理 yii2在程序报错时, 会执行指定action, 通过重写ErrorAction, 实现Bug自动提交至GitLab的issue 步骤 配置SiteController中的actions方法 public function actions(){return [error > [class > app\helpers\web\ErrorAction,],];}重写Error…...
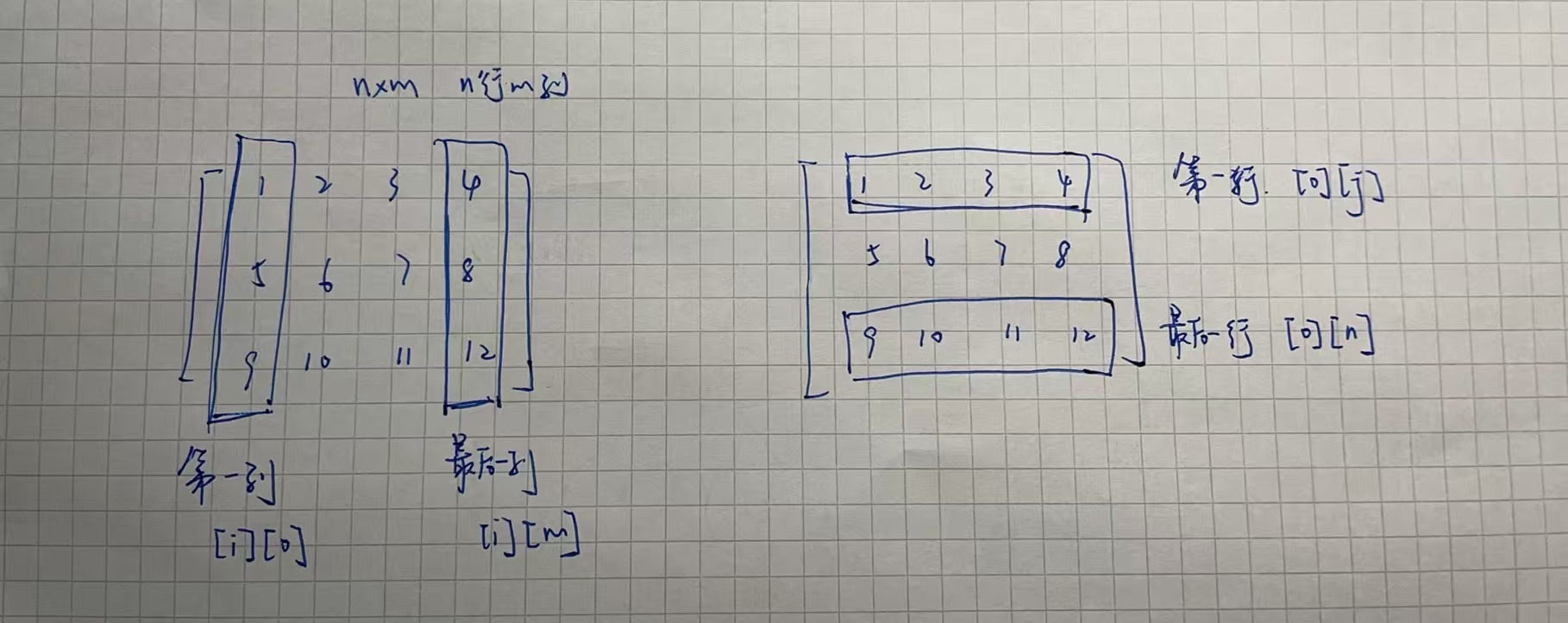
二维数组 行列混淆区分 js
二维数组定义 行 row:是“横着的一整行” 列 column:是“竖着的一整列” 在 JavaScript 里访问二维数组 grid[i][j] 表示 第i行第j列的元素 let grid [[1, 2, 3], // 第0行[4, 5, 6], // 第1行[7, 8, 9] // 第2行 ];// grid[i][j] 表示 第i行第j列的…...

MCP和Function Calling
MCP MCP(Model Context Protocol,模型上下文协议) ,2024年11月底,由 Anthropic 推出的一种开放标准,旨在统一大模型与外部数据源和工具之间的通信协议。MCP 的主要目的在于解决当前 AI 模型因数据孤岛限制而…...

