Leetcode 第 129 场双周赛题解
Leetcode 第 129 场双周赛题解
- Leetcode 第 129 场双周赛题解
- 题目1:3127. 构造相同颜色的正方形
- 思路
- 代码
- 复杂度分析
- 题目2:3128. 直角三角形
- 思路
- 代码
- 复杂度分析
- 题目3:3129. 找出所有稳定的二进制数组 I
- 思路
- 代码
- 复杂度分析
- 题目4:3130. 找出所有稳定的二进制数组 II
- 思路
- 代码
- 复杂度分析
Leetcode 第 129 场双周赛题解
题目1:3127. 构造相同颜色的正方形
思路
枚举 + 计数。
枚举矩阵中的每个 2×2 子矩形。
对于每个子矩形,统计 B 和 W 的个数,如果其中一个字母的出现次数 ≥3,则返回 true。
如果 4 个子矩形都不满足要求,返回 false。
代码
/** @lc app=leetcode.cn id=3127 lang=cpp** [3127] 构造相同颜色的正方形*/// @lc code=start
class Solution
{
public:bool canMakeSquare(vector<vector<char>> &grid){// 判断以 (row, col) 为左上角的 2*2 的正方形是否满足要求auto check = [&](int row, int col) -> bool{int cntB = 0, cntW = 0;for (int i = row; i <= row + 1; i++)for (int j = col; j <= col + 1; j++){if (grid[i][j] == 'B')cntB++;elsecntW++;}return cntB >= 3 || cntW >= 3;};// 对于 3*3 的矩阵,只需要考虑 4 种情况return check(0, 0) || check(0, 1) || check(1, 0) || check(1, 1);}
};
// @lc code=end
复杂度分析
时间复杂度:O(1)。
空间复杂度:O(1)。
题目2:3128. 直角三角形
思路
套路:有三个顶点,枚举「中间」的直角顶点更容易计算。
设第 i 行有 rows[i] 个 1,第 j 列有 cols[j] 个 1。根据乘法原理,直角顶点为 (i,j) 的直角三角形有 (rows[i] - 1) * (cols[j] - 1) 个,加到答案中。
代码
/** @lc app=leetcode.cn id=3128 lang=cpp** [3128] 直角三角形*/// @lc code=start
class Solution
{
public:long long numberOfRightTriangles(vector<vector<int>> &grid){int m = grid.size(), n = m ? grid[0].size() : 0;// 每行 1 的个数vector<int> rows(m, 0);for (int i = 0; i < m; i++){int row = 0;for (int j = 0; j < n; j++)row += grid[i][j];rows[i] = row;}// 每列 1 的个数vector<int> cols(n, 0);for (int j = 0; j < n; j++){int col = 0;for (int i = 0; i < m; i++)col += grid[i][j];cols[j] = col;}long long ans = 0LL;for (int i = 0; i < m; i++)for (int j = 0; j < n; j++)if (grid[i][j] == 1){// 直角顶点为 (i,j) 的直角三角形有 (rows[i] - 1) * (cols[j] - 1) 个ans += (rows[i] - 1) * (cols[j] - 1);}return ans;}
};
// @lc code=end
复杂度分析
时间复杂度:O(m*n),其中 m 和 n 分别是矩阵 grid 的行数和列数。
空间复杂度:O(m+n),其中 m 和 n 分别是矩阵 grid 的行数和列数。
题目3:3129. 找出所有稳定的二进制数组 I
思路
记忆化搜索。
dfs(i, j, count) 表示还剩 i 个 0,j 个 1,已经连用 count 个 i 对应的数字的组合数。
边界:dfs(0, 0, count) = 1。
转移为:
- 当 count == limit 时,换另一个数字开始计数 dfs(j-1, i, 1)
- 当 count < limit 时,为 dfs(i-1, j, count+1) + dfs(j-1, i, 1)
入口:dfs(zero, one, 0)。
代码
/** @lc app=leetcode.cn id=3129 lang=cpp** [3129] 找出所有稳定的二进制数组 I*/// @lc code=start
class Solution
{
private:const int MOD = 1e9 + 7;public:int numberOfStableArrays(int zero, int one, int limit){int mx = max(zero, one);int memo[mx + 1][mx + 1][limit + 1];memset(memo, -1, sizeof(memo));// 还剩 i 个 0,j 个 1,已经连续使用了 count 个 i 对应的数字function<int(int, int, int)> dfs = [&](int i, int j, int count) -> int{if (i < 0 || j < 0)return 0;if (i == 0 && j == 0)return 1;int &res = memo[i][j][count];if (res != -1)return res;if (count == limit){// 换另一个数字开始计数res = dfs(j - 1, i, 1) % MOD;}else{// 两种都可以res = (dfs(i - 1, j, count + 1) + dfs(j - 1, i, 1)) % MOD;}return res;};return dfs(zero, one, 0);}
};
// @lc code=end
复杂度分析
时间复杂度:O(zero*one*limit)。
空间复杂度:O(mx2*limit),其中 mx = max(zero, one)。
题目4:3130. 找出所有稳定的二进制数组 II
思路
题解:两种方法:动态规划 / 组合数学(Python/Java/C++/Go)
定义 dfs(i, j, k, limit) 为用 i 个 0,j 个 1 构造稳定数组的方案数,其中第 i+j 个位置要填 k,其中 k 为 0 或 1。

边界:

入口:dfs(zero, one, 0, limit) + dfs(zero, one, 1, limit)。
代码
/** @lc app=leetcode.cn id=3130 lang=cpp** [3130] 找出所有稳定的二进制数组 II*/// @lc code=start
class Solution
{
private:const int MOD = 1e9 + 7;public:int numberOfStableArrays(int zero, int one, int limit){int memo[zero + 1][one + 1][2];memset(memo, -1, sizeof(memo));// 用 i 个 0,j 个 1 构造稳定数组的方案数,其中第 i+j 个位置要填 kfunction<int(int, int, int, int)> dfs = [&](int i, int j, int k, int limit) -> int{if (i == 0){ // 递归边界return k == 1 && j <= limit;}if (j == 0){ // 递归边界return k == 0 && i <= limit;}int &res = memo[i][j][k];if (res != -1)return res;if (k == 0){res = ((long long)dfs(i - 1, j, 0, limit) + dfs(i - 1, j, 1, limit) +(i > limit ? MOD - dfs(i - limit - 1, j, 1, limit) : 0)) %MOD;}else{res = ((long long)dfs(i, j - 1, 0, limit) + dfs(i, j - 1, 1, limit) +(j > limit ? MOD - dfs(i, j - limit - 1, 0, limit) : 0)) %MOD;}return res;};return (dfs(zero, one, 0, limit) + dfs(zero, one, 1, limit)) % MOD;}
};
// @lc code=end
复杂度分析
时间复杂度:O(zero*one)。
空间复杂度:O(zero*one)。
相关文章:

Leetcode 第 129 场双周赛题解
Leetcode 第 129 场双周赛题解 Leetcode 第 129 场双周赛题解题目1:3127. 构造相同颜色的正方形思路代码复杂度分析 题目2:3128. 直角三角形思路代码复杂度分析 题目3:3129. 找出所有稳定的二进制数组 I思路代码复杂度分析 题目4:…...
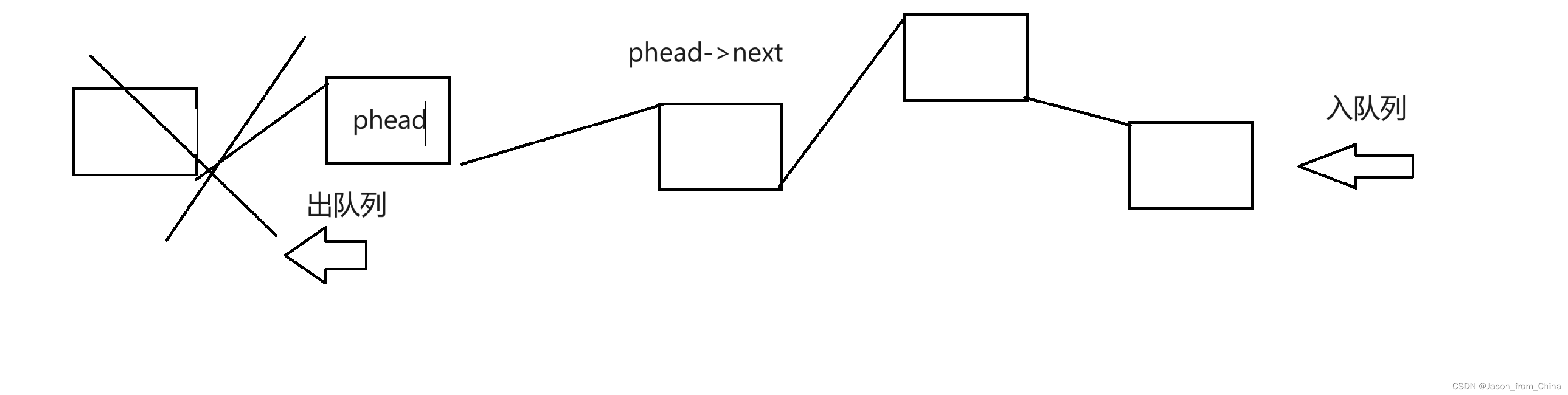
队列的讲解
队列的概念 队列:只允许在一端进行插入数据操作,在另一端进行删除数据操作的特殊线性表,队列具有先进先出FIFO(First In First Out) 入队列:进行插入操作的一端称为队尾 出队列:进行删除操作的一端称为队头 一端进另一端出 也就是可以做到,先…...
)
算法学习笔记(LCA)
L C A LCA LCA:树上两个点的最近公共祖先。(两个节点所有公共祖先中,深度最大的公共祖先) L C A LCA LCA的性质: 在所有公共祖先中, L C A ( x , y ) LCA(x,y) LCA(x,y)到 x x x和 y y y的距离都最短。 x …...

记一次苹果appstore提审拒审问题1.2
有关苹果appstore审核1.2问题的处理方案 2023.8.6苹果回复 Bug Fix Submissions The issues weve identified below are eligible to be resolved on your next update. If this submission includes bug fixes and youd like to have it approved at this time, reply to thi…...
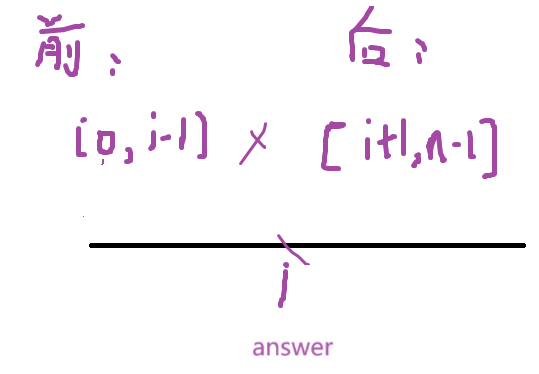
在做题中学习(59):除自身以为数组的乘积
238. 除自身以外数组的乘积 - 力扣(LeetCode) 解法:前缀积和后缀积 思路:answer中的每一个元素都是除自己以外所有元素的和。那就处理一个前缀积数组和后缀积数组。 而前缀积(f[i])是:[0,i-1]所有元素的乘积 后缀…...

centos 把nginx更新到最新版本
yum install epel-release # 添加 EPEL 软件仓库,这是 Nginx 官方软件仓库的依赖项 yum install yum-utils # yum-utils 包含了 yum-config-manager 工具,它可以让您轻松地启用、禁用或配置 yum 软件仓库 vi /etc/yum.repos.d/nginx.repo # 增加以下内容…...
01.认识HTML及常用标签
目录 URL(统一资源定位系统) HTML(超文本标记语言) 1)html标签 2)head标签 3)title标签 4)body标签 标签的分类 DTD文档声明 基础标签 1)H系列标签 2)…...

从零开始:C++ String类的模拟实现
文章目录 引言1.类的基本结构2.构造函数和析构函数3.基本成员函数总结 引言 在C编程中,字符串操作是非常常见且重要的任务。标准库中的std::string类提供了丰富且强大的功能,使得字符串处理变得相对简单。然而,对于学习C的开发者来说&#x…...
银河麒麟服务器操作系统V10-SP2部署gitlab服务
安装依赖 yum -y install python3-policycoreutils openssh-server openssh-clients postfix cronie curl下载gitlab-ce-15.4.2-ce.0.el8.x86_64.rpm安装包。 wget --content-disposition https://packages.gitlab.com/gitlab/gitlab-ce/packages/el/8/gitlab-ce-15.4.2-ce.0…...
【计算机毕业设计】基于SSM+Vue的线上旅行信息管理系统【源码+lw+部署文档+讲解】
目录 1 绪论 1.1 研究背景 1.2 设计原则 1.3 论文组织结构 2 系统关键技术 2.1JSP技术 2.2 JAVA技术 2.3 B/S结构 2.4 MYSQL数据库 3 系统分析 3.1 可行性分析 3.1.1 技术可行性 3.1.2 操作可行性 3.1.3 经济可行性 3.1.4 法律可行性 3.2系统功能分析 3.2.1管理员功能分析 3.2.…...

链表CPP简单示例
链表创建 链表打印全部内容 获取链表长度 链表根据指定位置添加元素 链表根据指定位置删除元素 #include <iostream> using namespace std;// 1、创建结构体// typedef 经常在结构中使用 typedef 别名 typedef struct node {int date;struct node* next; // 必须要自己…...

智能EDM邮件群发工具哪个好?
企业之间的竞争日益激烈,如何高效、精准地触达目标客户,成为每个市场战略家必须面对的挑战。在此背景下,云衔科技凭借其前沿的AI技术和深厚的行业洞察,匠心推出了全方位一站式智能EDM邮件营销服务平台,重新定义了邮件营…...

低代码与AI技术发展:开启数字化新时代
随着数字化转型的深入推进,低代码和AI技术逐渐成为各行各业关注的焦点。这两种技术的发展不仅改变了传统开发模式,还为企业创新和产业升级提供了新契机。本文将探讨这两种技术在实际应用中的相互促进作用,以及它们为我国经济社会发展带来的机…...

风电功率预测 | 基于遗传算法优化BP神经网络实现风电功率预测(附matlab完整源码)
风电功率预测 风电功率预测 | 基于遗传算法优化BP神经网络实现风电功率预测(附matlab完整源码)完整代码风电功率预测 | 基于遗传算法优化BP神经网络实现风电功率预测(附matlab完整源码) 基于遗传算法优化BP神经网络是一种常见的方法,用于改进BP神经网络在风电功率预测中的性…...

uni-segmented-control插件使用
dcloud插件市场 前端/uniapp 1.HBuildX打开目标项目 2.进入dcloud插件市场下载目标插件 3.看到如下提示(已经可以在目标项目中使用插件啦) 4.项目正式使用...

被动防护不如主动出击
自网络的诞生以来,攻击威胁事件不断涌现,网络攻防对抗已然成为信息时代背景下的一场无硝烟的战争。然而,传统的网络防御技术,如防火墙和入侵检测技术,往往局限于一种被动的敌暗我明的防御模式,面对攻击者无…...
ollama离线部署llama3(window系统)
首先介绍下ollama是什么?Ollama是一个开源的大型语言模型服务工具,旨在为用户提供本地化的运行环境,满足个性化的需求。具体来说,Ollama是一个功能强大的开源框架,可以简化在Docker容器中部署和管理大型语言模型&a…...

基于Django实现的(bert)深度学习文本相似度检测系统设计
基于Django实现的(bert)深度学习文本相似度检测系统设计 开发语言:Python 数据库:MySQL所用到的知识:Django框架工具:pycharm、Navicat、Maven 系统功能实现 登录页面 注册页面:用户账号,密码…...
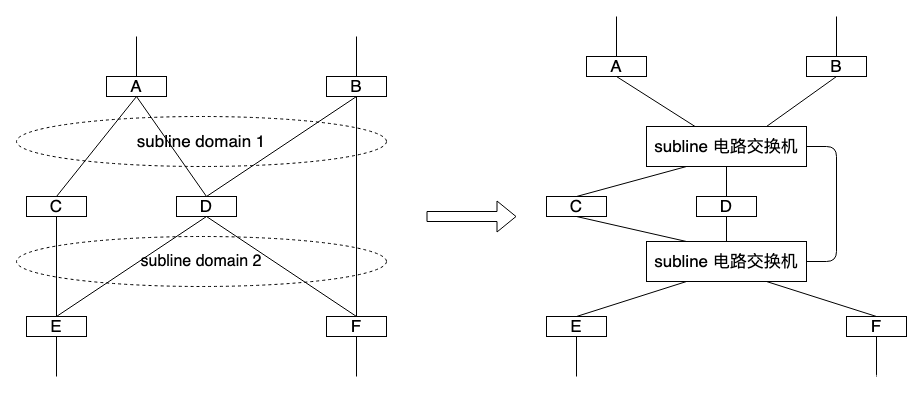
数据中心网络随想-电路交换
数据中心网络扩容并不容易,涉及设备上架,切换等又硬又大的动作,期间对所有应用都会产生影响,所以理论上 “加钱加硬件” 这种看起来很简单的事实际上真不如 “写一个随时部署升级的端到端拥塞控制算法” 更容易实施。 傍晚绕小区…...
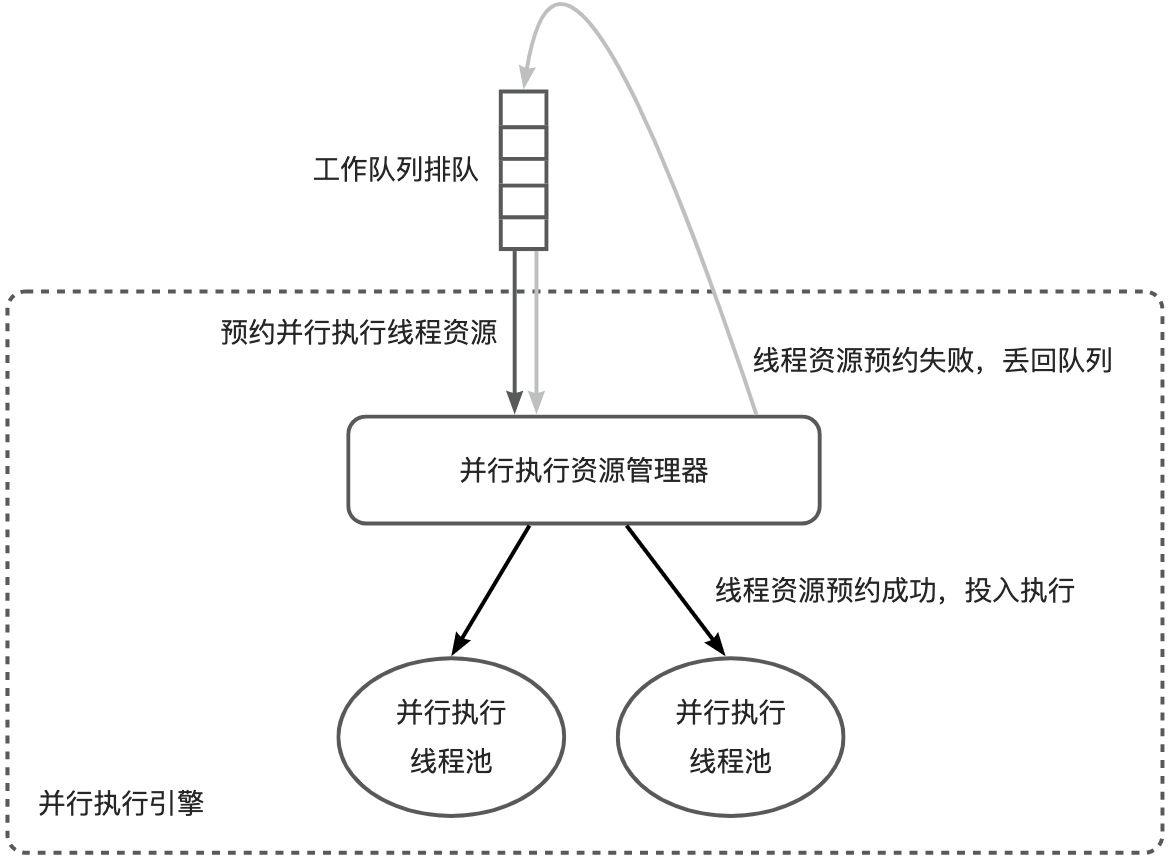
并行执行线程资源管理方式——《OceanBase 并行执行》系列 3
在某些特定场景下,由于需要等待线程资源,并行查询会遇到排队等待的情况。本篇博客将介绍如何管理并行执行线程资源,以解决这种问题。 《OceanBase并行执行》系列的内容分为七篇博客,本篇是其中的第三篇。 一并行执行概念二如何手…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...

论文阅读笔记——Muffin: Testing Deep Learning Libraries via Neural Architecture Fuzzing
Muffin 论文 现有方法 CRADLE 和 LEMON,依赖模型推理阶段输出进行差分测试,但在训练阶段是不可行的,因为训练阶段直到最后才有固定输出,中间过程是不断变化的。API 库覆盖低,因为各个 API 都是在各种具体场景下使用。…...

沙箱虚拟化技术虚拟机容器之间的关系详解
问题 沙箱、虚拟化、容器三者分开一一介绍的话我知道他们各自都是什么东西,但是如果把三者放在一起,它们之间到底什么关系?又有什么联系呢?我不是很明白!!! 就比如说: 沙箱&#…...

Unity VR/MR开发-VR开发与传统3D开发的差异
视频讲解链接:【XR马斯维】VR/MR开发与传统3D开发的差异【UnityVR/MR开发教程--入门】_哔哩哔哩_bilibili...

规则与人性的天平——由高考迟到事件引发的思考
当那位身着校服的考生在考场关闭1分钟后狂奔而至,他涨红的脸上写满绝望。铁门内秒针划过的弧度,成为改变人生的残酷抛物线。家长声嘶力竭的哀求与考务人员机械的"这是规定",构成当代中国教育最尖锐的隐喻。 一、刚性规则的必要性 …...

跨平台商品数据接口的标准化与规范化发展路径:淘宝京东拼多多的最新实践
在电商行业蓬勃发展的当下,多平台运营已成为众多商家的必然选择。然而,不同电商平台在商品数据接口方面存在差异,导致商家在跨平台运营时面临诸多挑战,如数据对接困难、运营效率低下、用户体验不一致等。跨平台商品数据接口的标准…...
