凸优化理论学习三|凸优化问题(一)
系列文章目录
凸优化理论学习一|最优化及凸集的基本概念
凸优化理论学习二|凸函数及其相关概念
文章目录
- 系列文章目录
- 一、优化问题
- (一)标准形式的优化问题
- (二)可行点和最优点
- (三)局部最优点
- (四)隐式和显式约束
- (五)可行性问题
- 二、凸优化问题
- (一)标准形式的凸优化问题
- (二)局部最优与全局最优
- (三)一些标准凸问题
- 1、线性规划 (LP)
- 2、二次规划 (QP)
- 3、二次约束二次规划 (QCQP)
- 4、二阶锥规划(SOCP)
- 4、凸椎形式问题
- 5、半定规划 (SDP)
- 6、LP、SOCP与SDP
一、优化问题
(一)标准形式的优化问题
- 优化目标:minimize f 0 ( x ) f_0(x) f0(x)
- 约束条件:
- 非等式约束: f i ( x ) ≤ 0 , i = 1 , . . . , m f_i(x)\leq0,i=1,...,m fi(x)≤0,i=1,...,m
- 等式约束: h i ( x ) = 0 , i = 1 , . . . , p h_i(x)=0,i=1,...,p hi(x)=0,i=1,...,p
(二)可行点和最优点
- 如果 x ∈ d o m f 0 x ∈ dom f_0 x∈domf0 并且满足约束条件,则 x ∈ R n x ∈ R_n x∈Rn 是可行的
- 最优值 p ∗ = i n f { f 0 ( x ) ∣ f i ( x ) ≤ 0 , i = 1 , . . . , m , h i ( x ) = 0 , i = 1 , . . . , p } p^{*}=inf\{f_0(x)|f_i(x)\leq 0,i=1,...,m,h_i(x)=0,i=1,...,p\} p∗=inf{f0(x)∣fi(x)≤0,i=1,...,m,hi(x)=0,i=1,...,p}
- 如果问题不可行,则 p ∗ = ∞ p^{*}=∞ p∗=∞
- 如果问题无下界,则 p ∗ = − ∞ p^{*}=-∞ p∗=−∞
- 如果 f 0 ( x ) = p ∗ f_0(x)=p^{*} f0(x)=p∗,则可行点 x x x是最优点
- X o p t X_{opt} Xopt是最优点的集合
(三)局部最优点
如果存在 R > 0 R > 0 R>0 使得 x 在以下情况下是最优的:
- m i n i m i z e ( o v e r z ) f 0 ( z ) minimize\ (over\ z)\ \ f_0(z) minimize (over z) f0(z)
- s u b j e c t t o subject\ to subject to
- f i ( z ) ≤ 0 , i = 1 , . . . , m f_i(z)\leq 0,i=1,...,m fi(z)≤0,i=1,...,m
- h i ( z ) = 0 , i = 1 , . . . , p h_i(z)=0,i=1,...,p hi(z)=0,i=1,...,p
- ∣ ∣ z − x ∣ ∣ 2 ≤ R ||z-x||_2\leq R ∣∣z−x∣∣2≤R
那么 x x x即为局部最优点。

(四)隐式和显式约束
- 显式约束:
- 非等式约束: f i ( x ) ≤ 0 , i = 1 , . . . , m f_i(x)\leq0,i=1,...,m fi(x)≤0,i=1,...,m
- 等式约束: h i ( x ) = 0 , i = 1 , . . . , p h_i(x)=0,i=1,...,p hi(x)=0,i=1,...,p
- 如果 m = p = 0 m=p=0 m=p=0,即没有约束,此时问题为无约束问题
- 标准形式优化问题具有隐式约束
x ∈ D = ⋂ i = 0 m d o m f i ∩ ⋂ i = 1 p d o m h i x\in D=⋂^m_{i=0}domf_i∩⋂^p_{i=1}domh_i x∈D=i=0⋂mdomfi∩i=1⋂pdomhi
(五)可行性问题
如果目标函数恒等于零,那么其最优解要么是零(如果可行集非空),要么是∞(如果可行集是空集)。我们称其为可行性问题:
- 目标:0
- 约束条件:
- f i ( x ) ≤ 0 , i = 1 , . . . , m f_i(x)\leq 0,i=1,...,m fi(x)≤0,i=1,...,m
- h i ( x ) = 0 , i = 1 , . . . , p h_i(x)=0,i=1,...,p hi(x)=0,i=1,...,p
二、凸优化问题
(一)标准形式的凸优化问题
- 目标:最小化 f 0 ( x ) f_0(x) f0(x)
- 约束条件:
- f i ( x ) ≤ 0 , i = 1 , . . . , m f_i(x)\leq 0,i=1,...,m fi(x)≤0,i=1,...,m
- a i T x = b i , i = 1 , . . . , p a_i^Tx=b_i,i=1,...,p aiTx=bi,i=1,...,p
其中:目标和不等式约束 f 0 , f 1 , . . . , f m f_0, f_1, ..., f_m f0,f1,...,fm是凸的;等式约束是仿射的,通常写为 A x = b Ax = b Ax=b;凸优化问题的可行集和最优集是凸的;如果 f 0 f_0 f0 是拟凸的, f 1 , . . . , f m f_1, ..., f_m f1,...,fm 是凸的, h 1 , . . . , h p h_1, ..., h_p h1,...,hp 是仿射的,则问题是拟凸的。
考虑一个标准形式问题的例子:
- 目标:最小化 f 0 ( x ) = x 1 2 + x 2 2 f_0(x)=x_1^2+x_2^2 f0(x)=x12+x22
- 约束条件:
- f 1 ( x ) = x 1 ( 1 + x 2 2 ) ≤ 0 f_1(x)=\frac{x_1}{(1+x_2^2)}\leq 0 f1(x)=(1+x22)x1≤0
- h 1 ( x ) = ( x 1 + x 2 ) 2 = 0 h_1(x)=(x_1+x_2)^2=0 h1(x)=(x1+x2)2=0
易知目标函数 f 0 f_0 f0是凸的,并且可行集 { ( x 1 , x 2 ) ∣ x 1 = − x 2 ≤ 0 } \{(x_1,x_2)|x_1=-x_2\leq0\} {(x1,x2)∣x1=−x2≤0}也是凸的;但是约束条件 f 1 f_1 f1不是凸的, h 1 h_1 h1不是仿射的,因此它不是一个凸问题。这个问题可以等价为以下凸问题:
- 目标:最小化 x 1 2 + x 2 2 x_1^2+x_2^2 x12+x22
- 约束条件:
- x 1 ≤ 0 x_1\leq 0 x1≤0
- x 1 + x 2 = 0 x_1+x_2=0 x1+x2=0
(二)局部最优与全局最优
凸问题的任何局部最优点都是(全局)最优的

可微分 f 0 f_0 f0 的最优性准则:
对于凸问题,点 x x x是最优解的一个充分必要条件:
- 点 x x x是可行解,即 x x x属于可行集合 X X X
- 对于任何可行点 y y y,都满足梯度条件: ∇ 2 f 0 ( x ) T ( y − x ) ≥ 0 ∇^2f_0(x)^T(y-x)\geq 0 ∇2f0(x)T(y−x)≥0
这个条件表明,如果 x x x 是最优解,那么任何与之可行的点 y y y 的方向上的梯度内积都是非负的。这实际上是凸问题最优解的一个重要性质,称为一阶条件。这种条件确保了最优解的局部性质,即在最优解附近,目标函数不会在可行方向上下降。另一方面,如果 x x x 满足这个条件,那么根据凸优化的性质,它意味着 x x x 是最优解。这个条件表明,如果梯度与任何可行方向的变化都是非负的,那么该点是全局最优解的候选者。

如果梯度 ∇ f 0 ( x ) ∇f_0(x) ∇f0(x) 在点 x x x 处非零,则它确实定义了可行集 X X X 在点 x x x 处的一个支撑超平面。
应用举例:
- 无约束问题: x x x 最小化 f 0 ( x ) f_0 (x) f0(x) 当且仅当 ∇ f 0 ( x ) = 0 ∇f_0 (x) = 0 ∇f0(x)=0
- 等式约束问题: x x x 最小化 f 0 ( x ) f_0 (x) f0(x) 且满足 A x = b Ax = b Ax=b 当且仅当存在 v v v使得:
A x = b , ∇ f 0 ( x ) + A T v = 0 Ax=b,\ ∇f_0 (x)+A^Tv=0 Ax=b, ∇f0(x)+ATv=0 - 非负正交坐标系上的的最小化问题: x x x 最小化 R + n R^n_+ R+n 上的 f 0 ( x ) f_0 (x) f0(x) 当且仅当:
- x x x的所有分量非负: x ≥ 0 x\geq 0 x≥0
- 对于所有的分量 i i i,如果 x i = 0 x_i=0 xi=0,则其对应的梯度分量 ∇ f 0 ( x ) i ∇f_0 (x)_i ∇f0(x)i非负
- 对于所有的分量 i i i,如果 x i > 0 x_i>0 xi>0,则其对应的梯度分量 ∇ f 0 ( x ) i ∇f_0 (x)_i ∇f0(x)i等于0
(三)一些标准凸问题
1、线性规划 (LP)
线性规划(LP)是一种特殊形式的凸优化问题,其目标函数和约束函数都是仿射的,可行集是多面体(即由线性不等式和等式构成的凸多面体)。这使得线性规划问题具有一些特殊的性质和解决方法。
- 目标函数:最小化 c T x + d c^Tx+d cTx+d
- 约束条件: G x ≤ h Gx\leq h Gx≤h, A x = b Ax=b Ax=b

饮食问题:
分段线性最小化问题可以转化为线性规划(LP)问题
>等价的线性规划问题即为:
- 目标函数:最小化t
- 约束条件: a i T x + b i ≤ t , i = 1 , . . . , m a^T_ix+b_i\leq t,i=1,...,m aiTx+bi≤t,i=1,...,m, x ∈ R n , t ∈ R x\in R^n,t\in R x∈Rn,t∈R
这个线性规划问题的变量包括 x x x 和 t t t,约束条件描述了函数 f 0 ( x ) f_0 (x) f0(x) 的上确界(epigraph)。通过将凸分段线性函数转化为等价的线性规划问题,我们可以使用线性规划算法来求解原始的凸分段线性函数最小化问题。
多面体的切比雪夫中心:
Chebyshev center x c h e b x_{cheb} xcheb是多面体 P P P 的中心,即它是一个点,使得对于多面体 P P P 中的每个点 x x x,从 x c h e b x_{ cheb} xcheb到 x x x 的欧几里得距离小于或等于到 P P P 的边界的最大距离。这等价于说,Chebyshev center 是可以包容在 P P P 内的最大球的中心。中心 x c h e b x_{ cheb} xcheb和球的半径 r r r可以通过以下方式找到:
- 对于每个约束 a i T x ≤ b i a_i^Tx\leq b_i aiTx≤bi,要求在球 B B B内部找到与约束最靠近的点,即对于每个 i i i,找到最大化 a i T ( x c h e b + u ) a_i^T(x_{cheb}+u) aiT(xcheb+u)的 u u u,其中 ∣ ∣ u ∣ ∣ 2 ≤ r ||u||_2\leq r ∣∣u∣∣2≤r,这相当于在球内找到一个与约束最接近的边界点
- 找到这些最近的点的最小值,即最大化 r r r,同时满足所有约束。这等价于最大化球的半径,使得球包含在多面体P中。
用线性规划表示为:
- 最大化 r r r
- 约束条件: a i T x c h e b + r ∣ ∣ a i ∣ ∣ 2 ≤ b i , i = 1 , . . . , m a_i^Tx_{cheb}+r||a_i||_2\leq b_i,i=1,...,m aiTxcheb+r∣∣ai∣∣2≤bi,i=1,...,m
2、二次规划 (QP)
二次规划(Quadratic Programming,简称QP)是一种优化问题,其目标是最小化或最大化一个二次型目标函数,其变量受到一组线性等式和不等式约束的限制。通常的形式如下:
- 目标函数:最小化 ( 1 / 2 ) x T P x + q T x + r (1/2)x^TPx+q^Tx+r (1/2)xTPx+qTx+r
- 约束条件: G x ≤ h Gx\leq h Gx≤h, A x = b Ax=b Ax=b
其中, P P P是对称正定矩阵

最小二乘法:
- 目标函数:最小化 ‖ A x − b ‖ 2 ‖Ax − b‖_2 ‖Ax−b‖2
- 解析解: x ∗ = A † b x^* = A†b x∗=A†b ( A † A† A† 是伪逆)
- 可以添加线性约束,例如:
- x > 0 x> 0 x>0(非负最小二乘法)
- x 1 ≤ x 2 ≤ . . . ≤ x n x_1\leq x_2\leq ... \leq x_n x1≤x2≤...≤xn(等渗回归)
具有随机成本的线性规划:
- 目标函数:最小化 c ˉ T x + γ x T Σ x \bar{c}^Tx+\gamma x^T\Sigma x cˉTx+γxTΣx
- 约束条件: G x ≤ h , A x = b Gx\leq h,Ax=b Gx≤h,Ax=b
其中, c c c是随机成本, γ > 0 \gamma > 0 γ>0 为风险厌恶参数,控制预期成本和方差(风险)之间的权衡
3、二次约束二次规划 (QCQP)
二次约束二次规划(Quadratically Constrained Quadratic Programming,QCQP)问题是在二次目标函数下,满足一组二次不等式约束条件。通常的形式如下:
- 目标函数:最小化 ( 1 / 2 ) x T P 0 x + q 0 T x + r 0 (1/2)x^TP_0x+q_0^Tx+r_0 (1/2)xTP0x+q0Tx+r0
- 约束条件: ( 1 / 2 ) x T P i x + q i T x + r i , i = 1 , . . . , m (1/2)x^TP_ix+q_i^Tx+r_i,i=1,...,m (1/2)xTPix+qiTx+ri,i=1,...,m, A x = b Ax=b Ax=b
其中, P P P是对称正定矩阵,目标和约束是凸二次的;如果 P 1 , . . . , P m ∈ S n + + P_1,..., P_m ∈ S_n^++ P1,...,Pm∈Sn++,可行域是 m 个椭球与仿射集的交集。
4、二阶锥规划(SOCP)
Second-Order Cone Programming (SOCP)是一类凸优化问题,它涉及到二阶锥约束,通常具有以下形式:
- 目标函数:最小化 f T x f^Tx fTx
- 约束条件: ∣ ∣ A i x + b i ∣ ∣ 2 ≤ c i T x + d i , i = 1 , . . . , m ||A_ix+b_i||_2\leq c_i^Tx+d_i,i=1,...,m ∣∣Aix+bi∣∣2≤ciTx+di,i=1,...,m, F x = g Fx=g Fx=g
其中,不等式约束又叫二阶锥约束(SOC): ( A i x + b i , c i T x + d i ) ∈ s e c o n d − o r d e r c o n e i n R n i + 1 (A_ix+b_i,c_i^Tx+d_i)\in second-order\ cone\ in\ R^{n_i+1} (Aix+bi,ciTx+di)∈second−order cone in Rni+1。如果 n i = 0 n_i=0 ni=0,二阶锥规划就会退为线性规划,如果 c i = 0 c_i=0 ci=0,二阶锥规划退为二次约束二次规划 (QCQP)。
鲁棒线性规划问题: 假设约束向量 a i a_i ai是不确定的情况,也就是说鲁棒线性规划(Robust Linear Programming)涉及到在不确定条件下寻找最优解。
- 目标函数:最小化 c T x c^Tx cTx
- 约束条件: a i T x ≤ b i , i = 1 , . . . , m a_i^Tx\leq b_i,i=1,...,m aiTx≤bi,i=1,...,m
对于这种不确定性,常见的处理方式有确定性最坏情况方法和随机方法两种。
确定性最坏情况方法:约束必须适用于所有 a i ∈ E i a_i ∈ E_i ai∈Ei(不确定性椭球)
- 确定性最坏情况方法的基本形式:
- 目标函数:最小化 c T x c^Tx cTx
- 约束条件: a i T x ≤ b i f o r a l l a i ∈ E i , i = 1 , . . . , m a_i^Tx\leq b_i\ for\ all\ a_i\in E_i,i=1,...,m aiTx≤bi for all ai∈Ei,i=1,...,m
- 确定性最坏情况方法的原理:不确定性椭球形式为 E i = { a ˉ i + P i u ∣ ∣ ∣ u ∣ ∣ 2 ≤ 1 } E_i=\{\bar{a}_i+P_iu|\ ||u||_2\leq 1\} Ei={aˉi+Piu∣ ∣∣u∣∣2≤1},其中 a ˉ i ∈ R \bar{a}_i\in R aˉi∈R是中心, P i ∈ R n × n P_i\in R^{n\times n} Pi∈Rn×n是决定半轴的奇异值/奇异向量。最终可以等价于以下形式的二阶锥规划问题:
- 目标函数:最小化 c T x c^Tx cTx
- 约束条件: a ˉ i T x + ∣ ∣ P T i x ∣ ∣ 2 2 ≤ b i , i = 1 , . . . , m \bar{a}_i^Tx+||PT_ix||^2_2\leq b_i,i=1,...,m aˉiTx+∣∣PTix∣∣22≤bi,i=1,...,m
随机方法:把 a i a_i ai看成一个随机变量,约束必须以一定的概率 η \eta η成立
- 随机方法的基本形式
- 目标函数:最小化 c T x c^Tx cTx
- 约束条件: p r o b ( a i T x ≤ b i ) ≥ η , i = 1 , . . . , m prob(a_i^Tx\leq b_i)\geq \eta,i=1,...,m prob(aiTx≤bi)≥η,i=1,...,m
- 随机方法的基本原理:假设 a i ∼ N ( a ˉ i , Σ i ) a_i\sim N(\bar{a}_i,\Sigma_i) ai∼N(aˉi,Σi),所以 a i T x ∼ N ( a ˉ i T x , x T Σ i x ) a_i^Tx\sim N(\bar{a}_i^Tx,x^T\Sigma_ix) aiTx∼N(aˉiTx,xTΣix), p r o b ( a i T x ≤ b i ) = Φ ( b i − a ˉ i T x ∣ ∣ Σ i 1 / 2 x ∣ ∣ 2 ) prob(a_i^Tx\leq b_i)=\Phi(\frac{b_i-\bar{a}_i^Tx}{||\Sigma_i^{1/2}x||_2}) prob(aiTx≤bi)=Φ(∣∣Σi1/2x∣∣2bi−aˉiTx), p r o b ( a i T x ≤ b i ) ≥ η prob(a_i^Tx\leq b_i)\geq \eta prob(aiTx≤bi)≥η可以被表示 a ˉ i T x + Φ − 1 ( η ) ∣ ∣ Σ i 1 / 2 x ∣ ∣ 2 ≤ b i \bar{a}_i^Tx+\Phi^{-1}(\eta)||\Sigma_i^{1/2}x||_2\leq b_i aˉiTx+Φ−1(η)∣∣Σi1/2x∣∣2≤bi。当 η > 1 / 2 \eta > 1/2 η>1/2时,可以等价于以下形式的二阶锥规划问题:
- 目标函数:最小化 c T x c^Tx cTx
- 约束条件: a ˉ i T x + Φ − 1 ( η ) ∣ ∣ Σ i 1 / 2 x ∣ ∣ 2 ≤ b i , i = 1 , . . . , m \bar{a}_i^Tx+\Phi^{-1}(\eta)||\Sigma^{1/2}_ix||_2\leq b_i,i=1,...,m aˉiTx+Φ−1(η)∣∣Σi1/2x∣∣2≤bi,i=1,...,m
4、凸椎形式问题
在凸优化中,凸锥形式的问题是一种重要的形式,涉及到优化目标函数以及约束条件均为凸锥函数或凸锥集。具体而言,考虑以下凸锥形式的问题:
- 目标函数: 最小化 最小化 最小化c^Tx$
- 约束条件: F x + g ≤ K 0 Fx+g\leq_K 0 Fx+g≤K0, A x = b Ax=b Ax=b
其中, K K K表示一个凸椎,通常是一个封闭的凸椎
5、半定规划 (SDP)
半定规划(Semidefinite Programming,SDP)是一类重要的凸优化问题,它涉及到优化一个线性函数,其变量是对称半正定矩阵。半定规划的一般形式如下:
- 目标函数:最小化 c T x c^Tx cTx
- 约束条件: x 1 F 1 + x 2 F 2 + . . . + x n F n + G ≤ 0 x_1F_1+x_2F_2+...+x_nF_n+G\leq 0 x1F1+x2F2+...+xnFn+G≤0, A x = b Ax=b Ax=b
其中, F F F和 G G G为对称矩阵( F i , G ∈ S k F_i,G\in S^k Fi,G∈Sk),不等式约束称为线性矩阵不等式(LMI)。
示例:矩阵范数最小化
6、LP、SOCP与SDP
LP 和等效的 SDP:
 SOCP 和等效的 SDP:
SOCP 和等效的 SDP:

相关文章:

凸优化理论学习三|凸优化问题(一)
系列文章目录 凸优化理论学习一|最优化及凸集的基本概念 凸优化理论学习二|凸函数及其相关概念 文章目录 系列文章目录一、优化问题(一)标准形式的优化问题(二)可行点和最优点(三)局部最优点(四…...

【Unity Shader入门精要 第7章】基础纹理补充内容:MipMap原理
1.纹理采样 我们对纹理采样进行显示的过程,可以理解为将屏幕上的一个像素(下文用像素表示)映射到纹理上的一个像素(下文用纹素表示),然后用纹理上的这个像素的颜色进行显示。 理想情况下,屏幕…...

JeeSite Vue3:前端开发页面如何动态设置菜单展示模式?
推荐阅读: JeeSite Vue3:前端开发的未来之路(更新版) 随着技术的飞速发展,前端开发技术日新月异。在这个背景下,JeeSite Vue3 作为一个基于 Vue3、Vite、Ant-Design-Vue、TypeScript 和 Vue Vben Admin 的前端框架,引…...

微信小程序-禁止页面下拉回弹
微信小程序-禁止页面下拉回弹,主要是pages.json中的这3个配置: "enablePullDownRefresh": false, 这个配置项用于控制页面是否支持下拉刷新。当设置为false时,用户无法通过下拉页面来触发刷新操作。 "disableScroll": true, 这个配置项用于控…...
测试环境搭建整套大数据系统(十六:超级大文件处理遇到的问题)
一:yarn出现损坏的nodemanger 报错现象 日志:1/1 local-dirs usable space is below configured utilization percentage/no more usable space [ /opt/hadoop-3.2.4/data/nm-local-dir : used space above threshold of 90.0% ] ; 1/1 log-dirs usabl…...
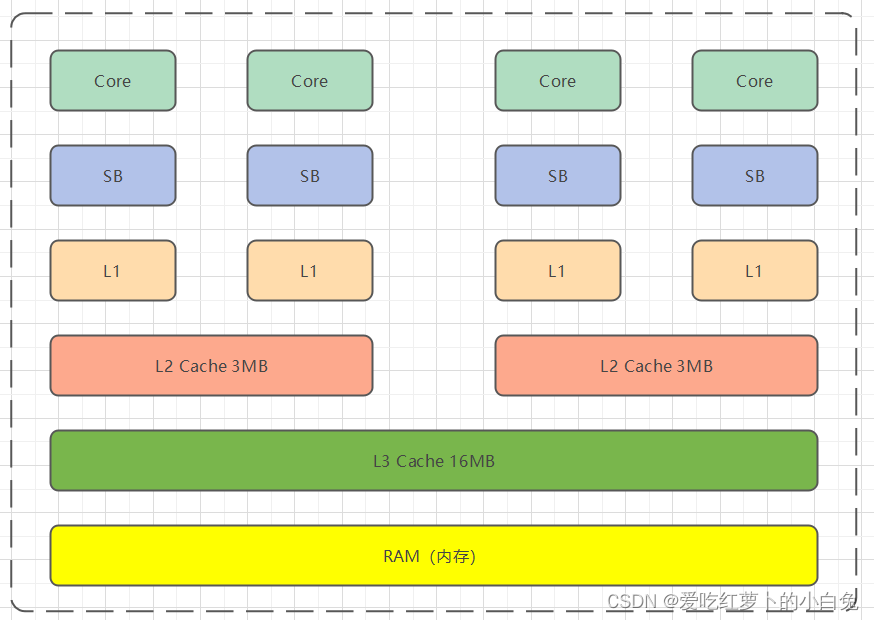
C++ 并发编程指南(11)原子操作 | 11.6、计算机内存结构
文章目录 一、计算机内存结构1、内存的基本组成2、内存的类型3、内存的结构层次4、CPU架构5、局部性原理6、总结 前言 在探讨计算机的运行效率和数据处理能力时,内存结构无疑是一个至关重要的部分。内存,作为计算机系统中的关键组件,承担着存…...

正则表达式教程
正则表达式在线工具网站:https://regexr.com...

SEO之为什么研究关键词(二)
初创企业需要建站的朋友看这篇文章,谢谢支持: 我给不会敲代码又想搭建网站的人建议 新手上云 (续上一篇。。。。。) 3、寻找有效流量 排名和流量都不是目的,有效流量带来的转化才是目的。就算公司有足够的实力将一些…...

Mysql 创建索引
1. 在创建表时添加索引 在使用CREATE TABLE语句创建表的同时,可以直接定义索引。例如,创建一个包含索引的表: CREATE TABLE clothes (id INT PRIMARY KEY,c_brand VARCHAR(100),c_type VARCHAR(50),c_size VARCHAR(10),price DECIMAL(10, 2…...

vaspkit 画 Charge-Density Difference
(echo 314;echo $(cat 1))|vaspkit 文件1提前写好使用的CHGCAR路径 SPIN_DW.vasp ../ML2scf/SPIN_DW.vasp ../ML1scf/SPIN_DW.vasp POSite and negative 默认为blue,and 青色 (RGB 30 245 245) 正值:blue 。负值:青色 RGB 30 245 245。 提示&…...

FreeRTOS缩小bss段的处理
bss太大了,有60多M,客户要求处理一下 readelf -s app.elf | grep "OBJECT" 发现有一条 592: 8800dd78 0x4000000 OBJECT LOCAL DEFAULT 15 ucHeap 长度64M,地址8800dd78刚好在bss段里,bss段地址如下ÿ…...

STM32数字示波器+详细注释+上位机程序+硬件
目录 1、设计指标: 2、功能: 3、上位机的程序 4、测试的照片 5、PCB 6、模拟电路板 7、程序 资料下载地址:STM32数字示波器详细注释上位机程序硬件 1、设计指标: 主控: STM32…...
【平衡二叉树】AVL树(双旋)
🎉博主首页: 有趣的中国人 🎉专栏首页: C进阶 🎉其它专栏: C初阶 | Linux | 初阶数据结构 小伙伴们大家好,本片文章将会讲解AVL树的左双选和右双旋的相关内容。 如果看到最后您觉得这篇文章写…...

【保姆级介绍自动化的讲解】
🌈个人主页: 程序员不想敲代码啊 🏆CSDN优质创作者,CSDN实力新星,CSDN博客专家 👍点赞⭐评论⭐收藏 🤝希望本文对您有所裨益,如有不足之处,欢迎在评论区提出指正,让我们共…...

【大数据面试题】27 讲下Doris的物化视图
一步一个脚印,一天一道面试题。 物化视图概念 物化视图,顾名思义,是将一个查询的结果预先计算并存储为物理表的形式。这意味着,原本需要在运行时动态执行的复杂查询,现在变成了直接从已经计算好的结果表中读取数据&a…...

kylin 使用心得
Kylin操作系统是一种基于Linux的操作系统,主要在中国使用,由中国国内的开发团队维护。它的目标是为了提供一个稳定、安全、易于使用的操作环境。以下是一些用户可能基于Kylin操作系统的使用心得: 1. **界面友好**:Kylin操作系统通…...
在线音乐系统
文章目录 在线音乐系统一、项目演示二、项目介绍三、部分功能截图四、部分代码展示五、底部获取项目(9.9¥带走) 在线音乐系统 一、项目演示 音乐网站 二、项目介绍 基于springbootvue的前后端分离在线音乐系统 登录角色 : 用户、管理员 用…...

LeetCode算法题:49. 字母异位词分组(Java)
给你一个字符串数组,请你将 字母异位词 组合在一起。可以按任意顺序返回结果列表。 字母异位词 是由重新排列源单词的所有字母得到的一个新单词。 示例 1: 输入: strs ["eat", "tea", "tan", "ate", "nat", …...
第五课,输入函数、布尔类型、比较运算和if判断
一,输入函数input() 与输出函数print()相对应的,是输入函数input(),前者是把程序中的数据展示给外界(比如电脑屏幕上),而后者是把外界(比如键盘)的数据输入进程序中 input()函数可…...
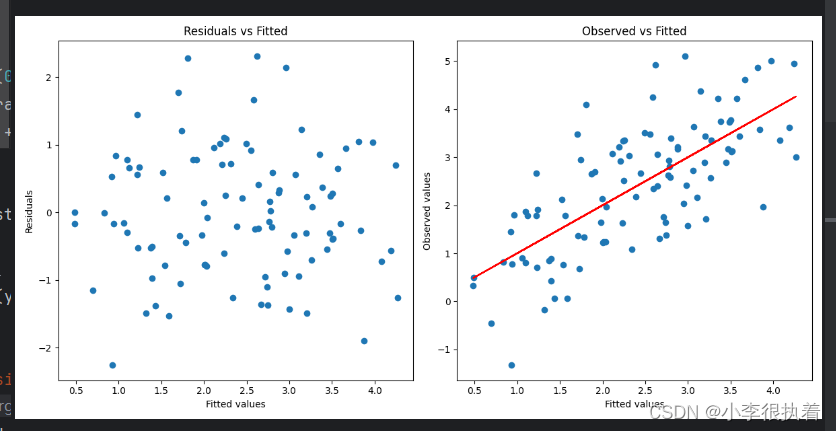
数学建模——线性回归模型
目录 1.线性回归模型的具体步骤和要点: 1.收集数据: 2.探索性数据分析: 3.选择模型: 4.拟合模型: 5.评估模型: 1.R平方(R-squared): 2.调整R平方(Ad…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...

tomcat入门
1 tomcat 是什么 apache开发的web服务器可以为java web程序提供运行环境tomcat是一款高效,稳定,易于使用的web服务器tomcathttp服务器Servlet服务器 2 tomcat 目录介绍 -bin #存放tomcat的脚本 -conf #存放tomcat的配置文件 ---catalina.policy #to…...

【免费数据】2005-2019年我国272个地级市的旅游竞争力多指标数据(33个指标)
旅游业是一个城市的重要产业构成。旅游竞争力是一个城市竞争力的重要构成部分。一个城市的旅游竞争力反映了其在旅游市场竞争中的比较优势。 今日我们分享的是2005-2019年我国272个地级市的旅游竞争力多指标数据!该数据集源自2025年4月发表于《地理学报》的论文成果…...



