【平衡二叉树】AVL树(双旋)


小伙伴们大家好,本片文章将会讲解
AVL树的左双选和右双旋的相关内容。
如果看到最后您觉得这篇文章写得不错,有所收获,麻烦点赞👍、收藏🌟、留下评论📝。您的支持是我最大的动力,让我们一起努力,共同成长!
文章目录
- `1. 左右双旋`
- `1. 右左双旋`
- `3. AVL的验证`
- `3. AVL的验证`
- `3. AVL的性能`
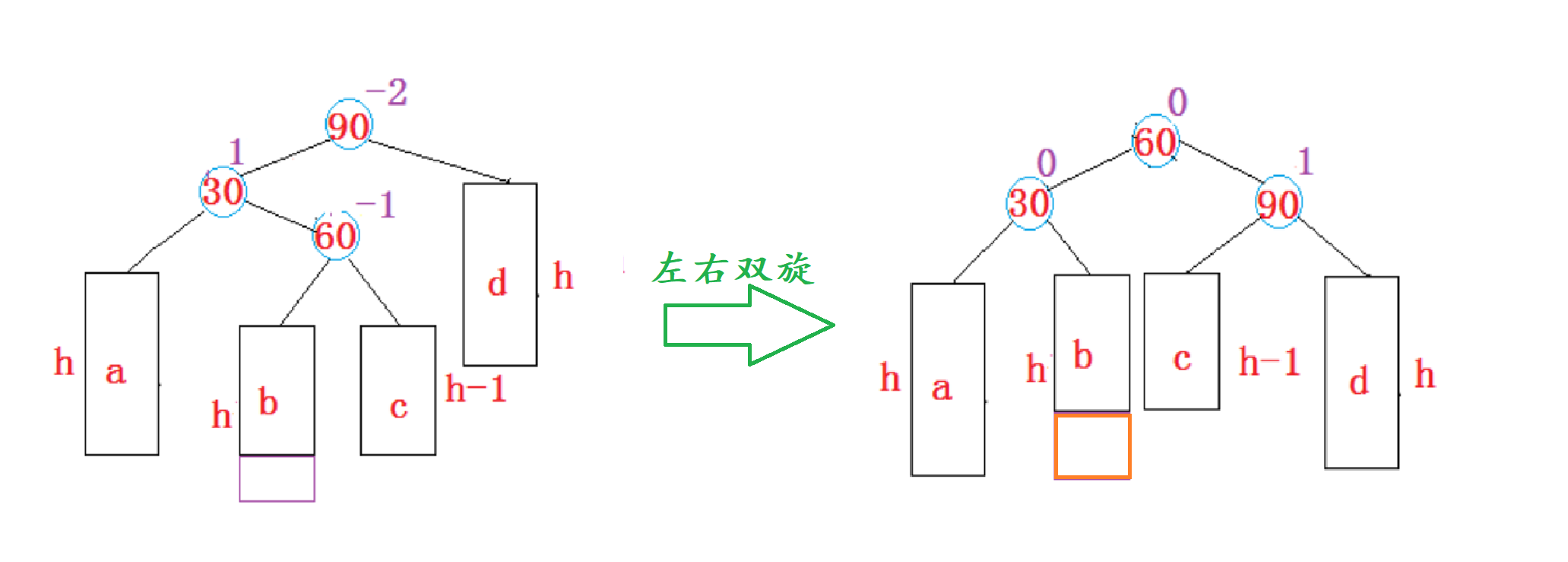
1. 左右双旋
⚡出现情况
1. 此处在30的左子树或者右子树新增节点都会引发旋转;
2. 如果单纯的对根节点进行右单旋,并不能解决左边高的问题,会变成右边高,所以要进行双旋,步骤如下:
1. 先对parent->left节点进行左单旋
2. 再对根节点进行右单旋
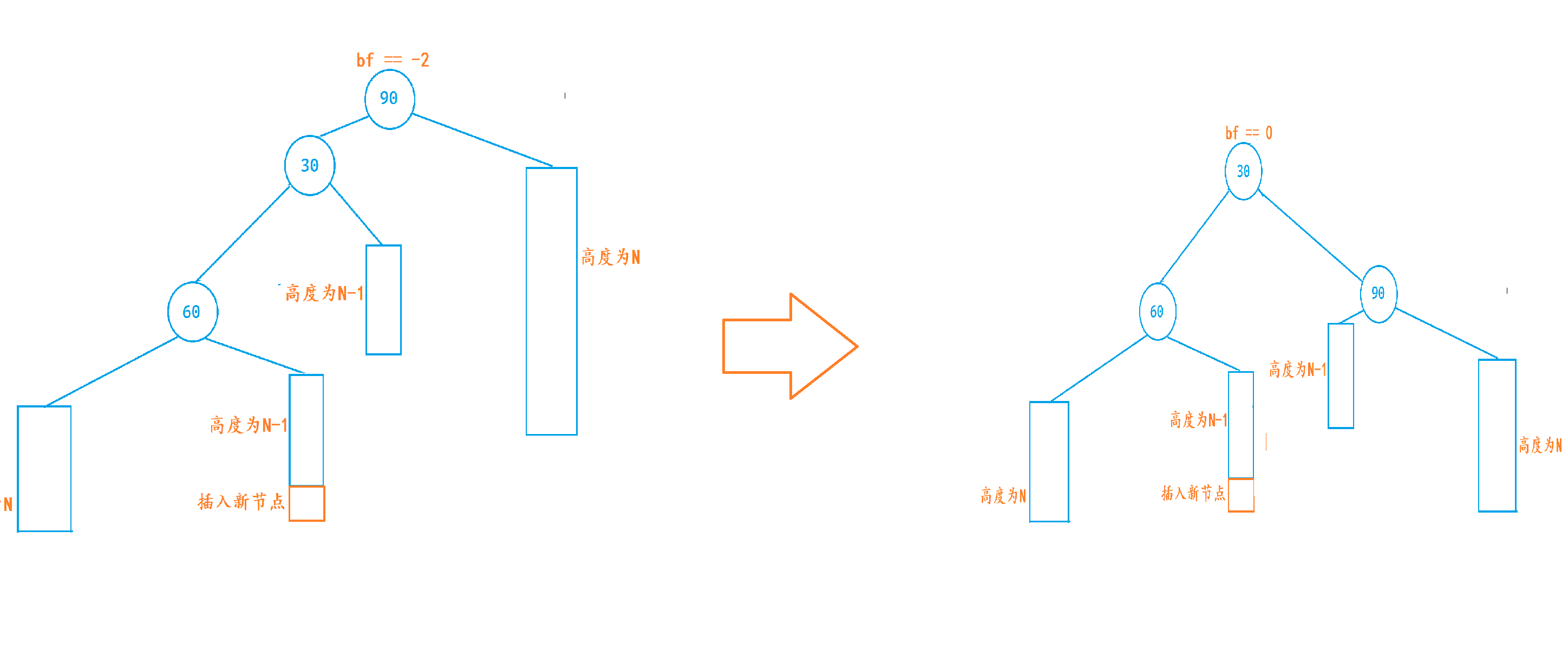
完整步骤
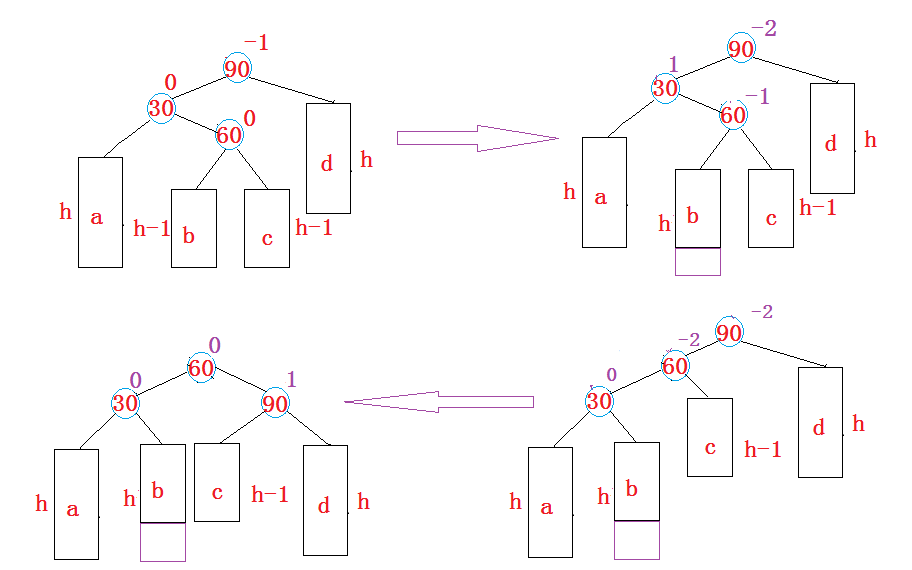
我们假设顶端节点叫做
parent,parent->left叫做subL,subL->right叫做subLR。
左右双旋后满足二叉搜索树的性质:
左右双旋后,实际上就是让
subLR的左子树和右子树,分别作为subL和parent的右子树和左子树,再让subL和parent分别作为subLR的左右子树,最后让subLR作为整个子树的根。
1.subLR的左子树当中的结点本身就比subL的值大,因此可以作为subL的右子树。
2.subLR的右子树当中的结点本身就比parent的值小,因此可以作为parent的左子树。
3. 经过步骤1、2后,subL及其子树当中结点的值都就比subLR的值小,而parent及其子树当中结点的值都就比subLR的值大,因此它们可以分别作为subLR的左右子树。
左右双旋后,平衡因子的更新随着subLR原始平衡因子的不同分为以下三种情况:
1、当
subLR原始平衡因子是-1时,左右双旋后parent、subL、subLR的平衡因子分别更新为1、0、0。
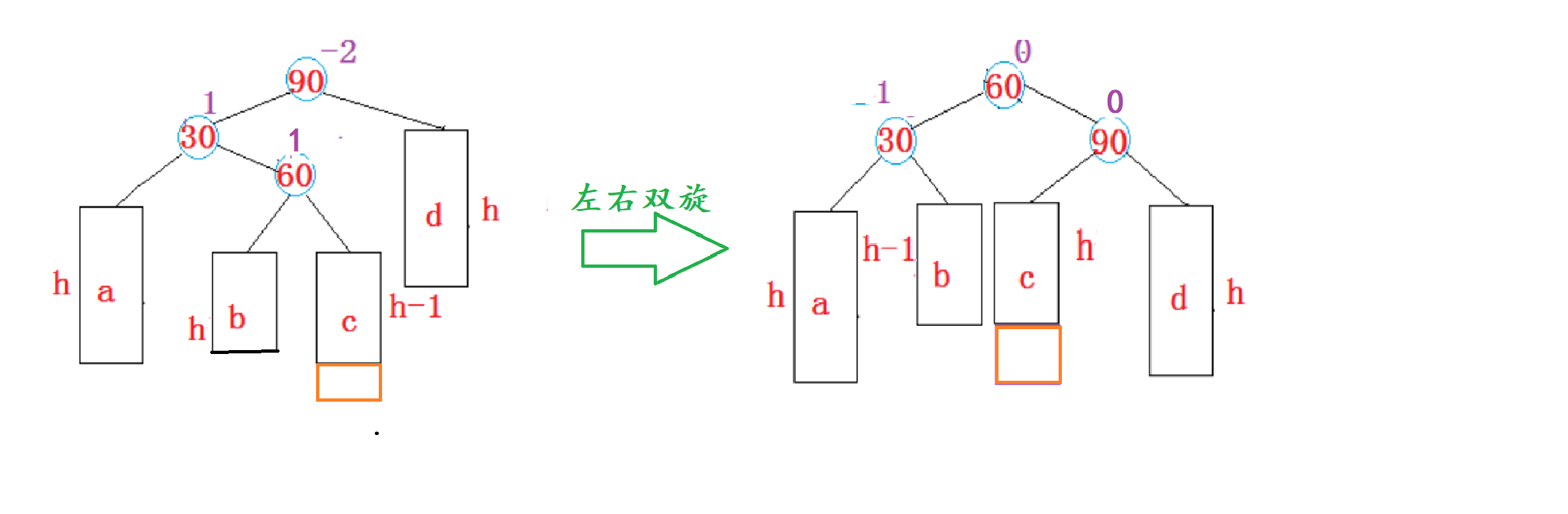
2、当
subLR原始平衡因子是1时,左右双旋后parent、subL、subLR的平衡因子分别更新为0、-1、0。
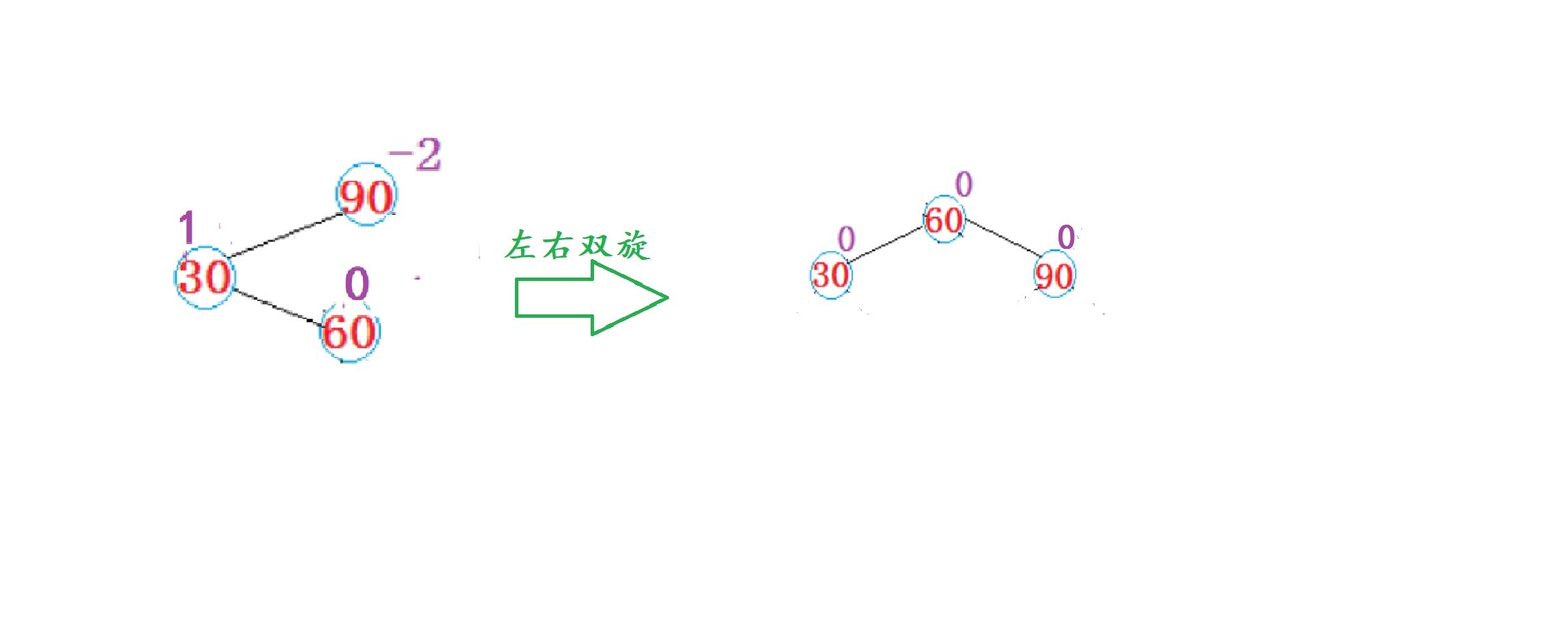
3、当
subLR原始平衡因子是0时,左右双旋后parent、subL、subLR的平衡因子分别更新为0、0、0。
代码如下:
void RotateLR(Node* parent)
{Node* subL = parent->_left;Node* subLR = subL->_right;int bf = subLR->_bf;//1、以subL为旋转点进行左单旋RotateL(subL);//2、以parent为旋转点进行右单旋RotateR(parent);if (bf == -1){subL->_bf = 0;parent->_bf = 1;subLR->_bf = 0;}else if (bf == 1){subL->_bf = -1;parent->_bf = 0;subLR->_bf = 0;}else if (bf == 0){subL->_bf = subLR->_bf = parent->_bf = 0;}else {assert(false);}
}
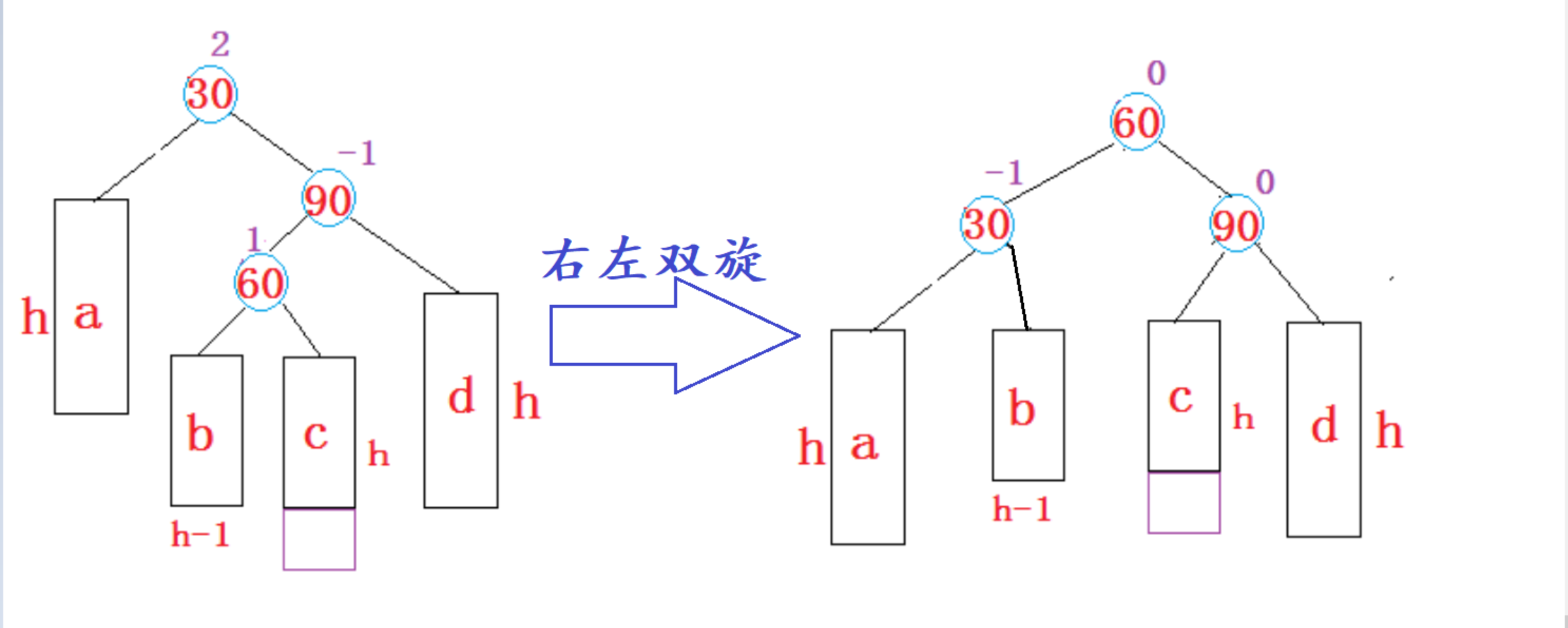
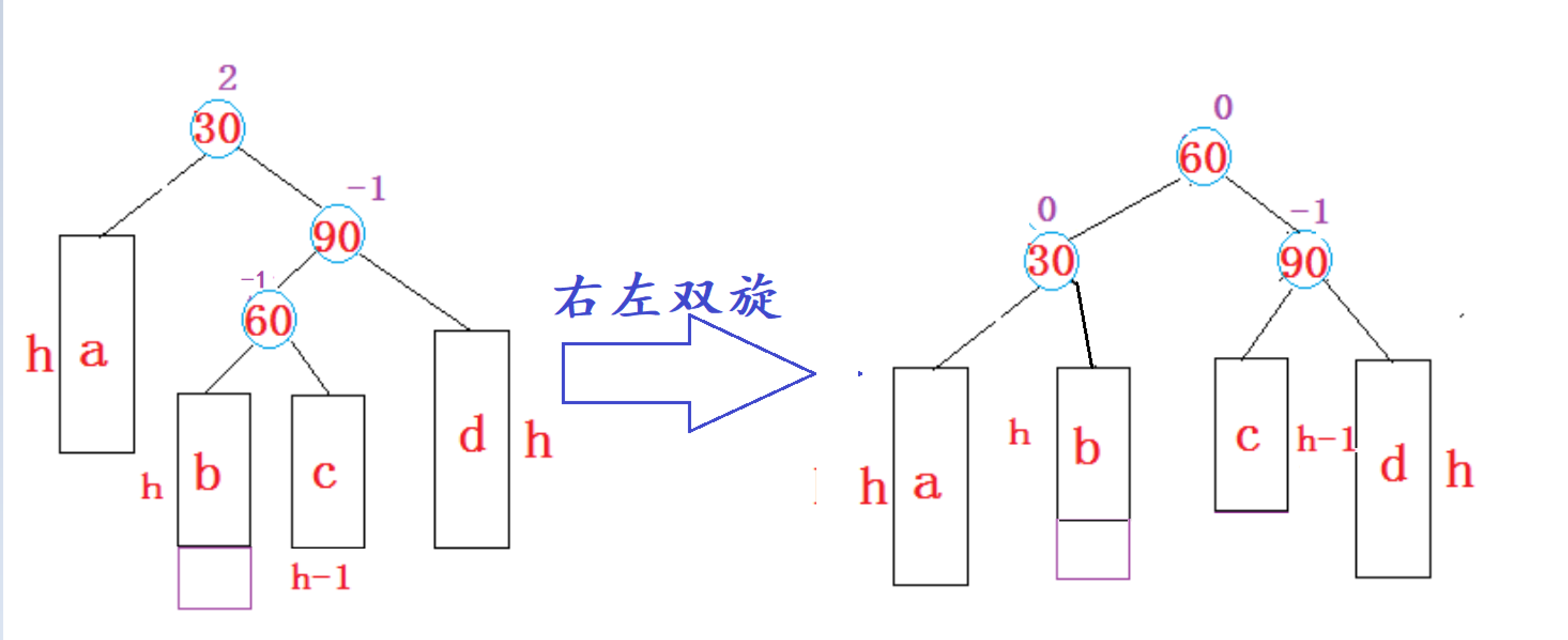
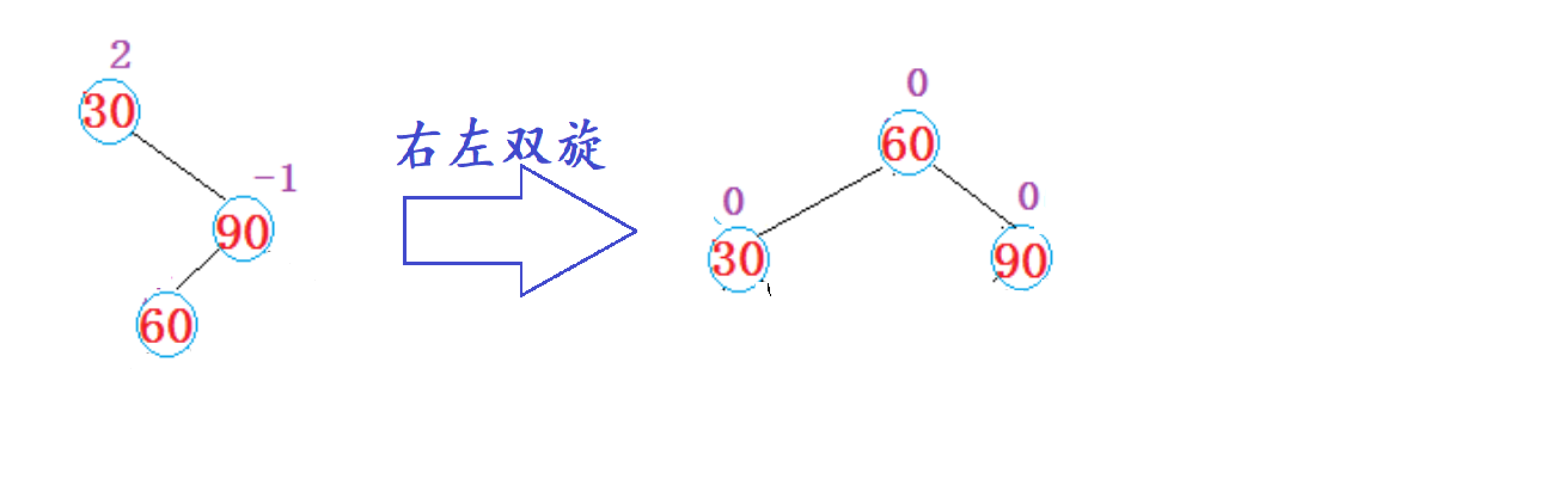
1. 右左双旋
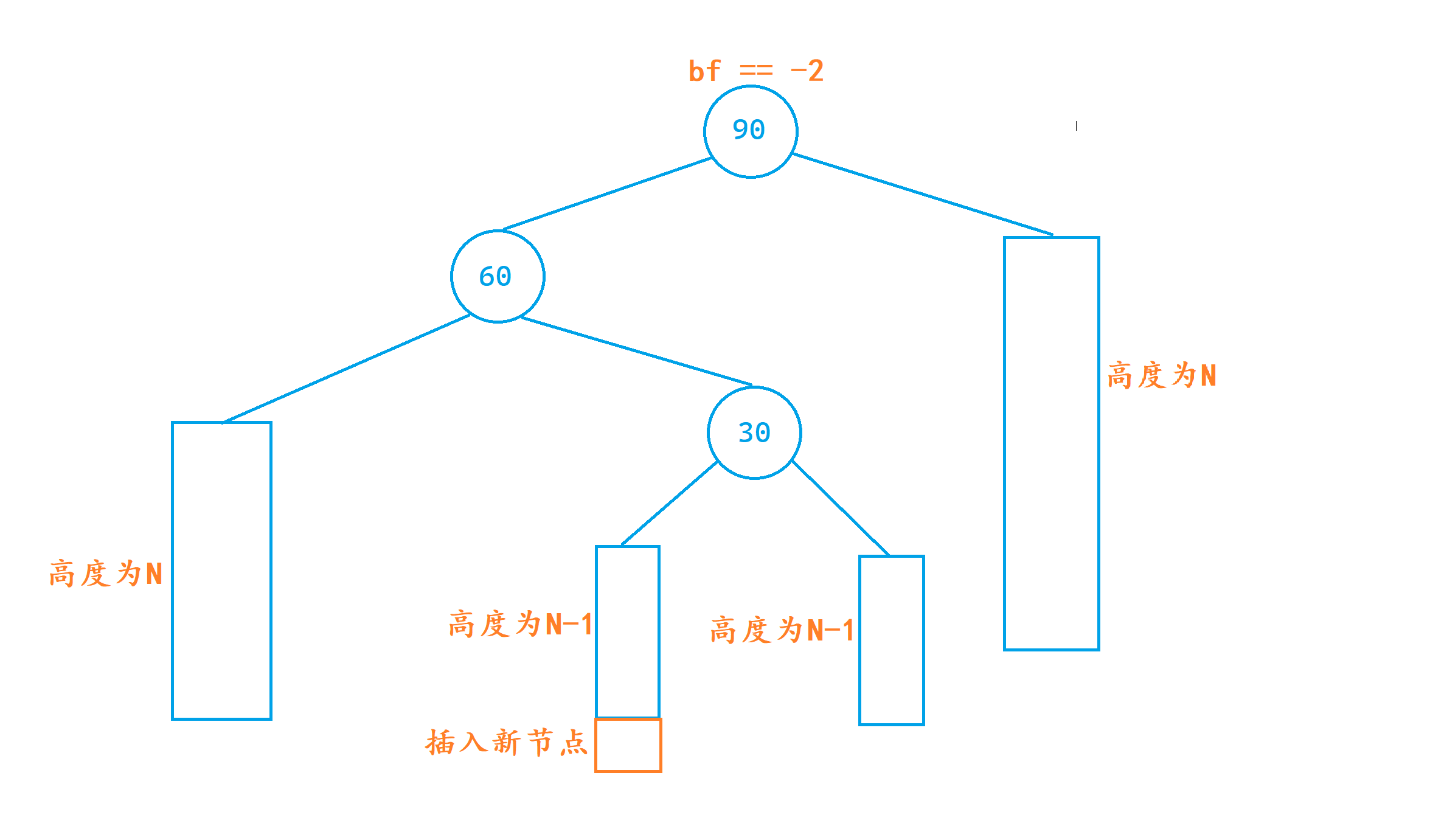
⚡出现情况
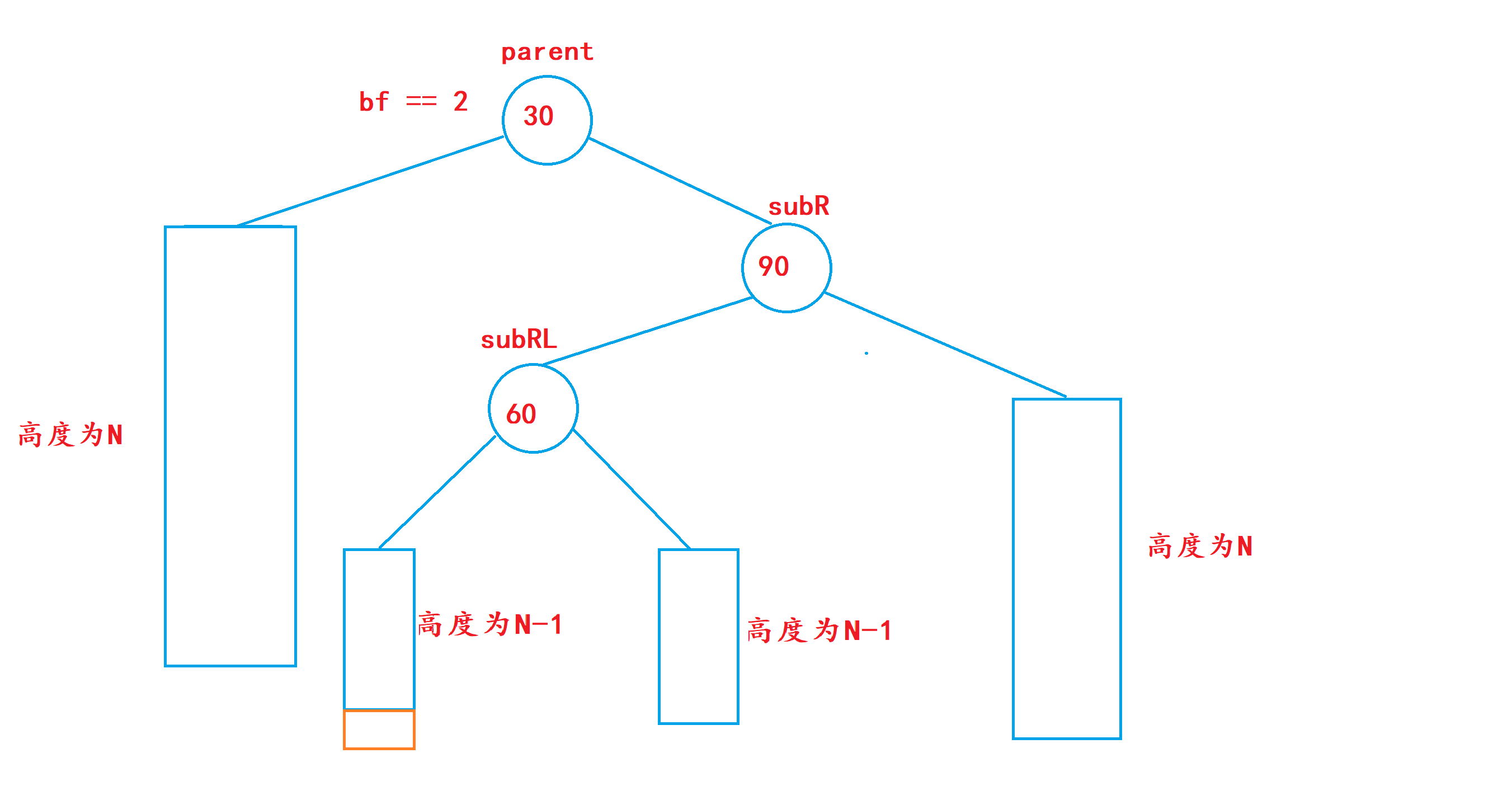
1. 此处在60的左子树或者右子树新增节点都会引发旋转;
2. 如果单纯的对根节点进行左单旋,并不能解决右边高的问题,会变成左边高,所以要进行双旋,步骤如下:
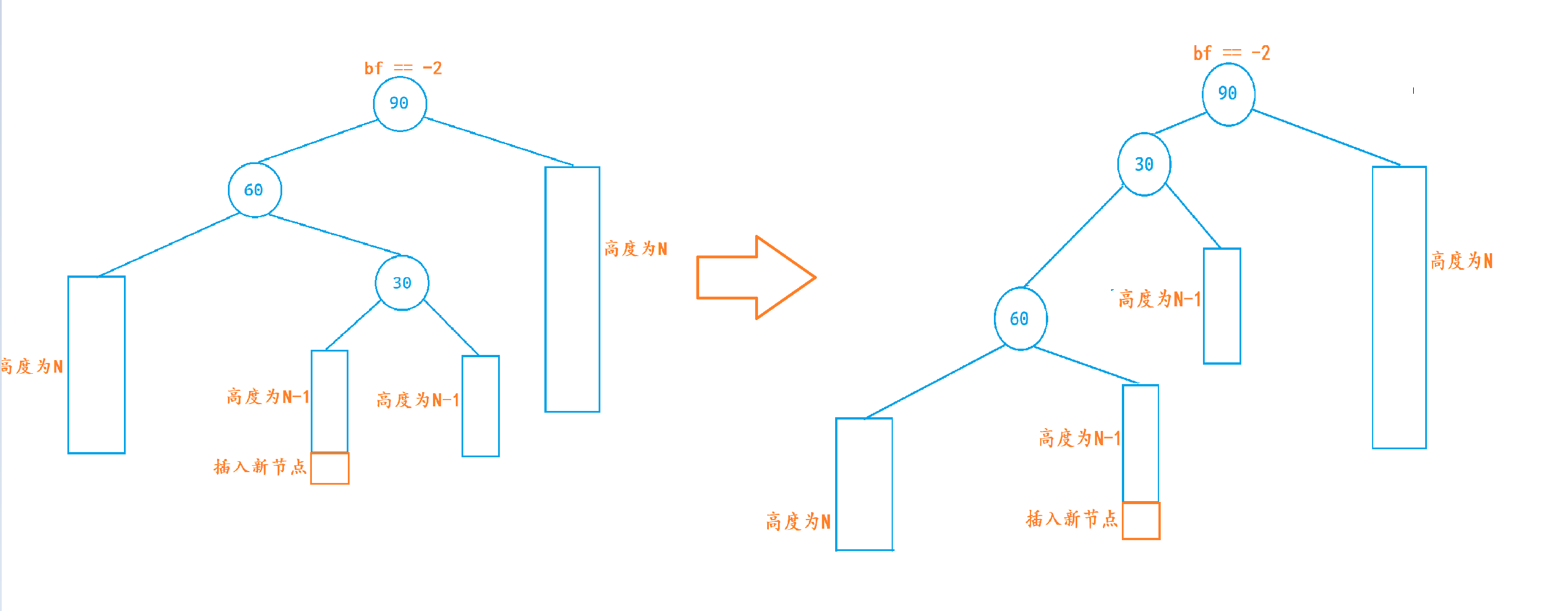
1. 先对subR节点进行右单旋
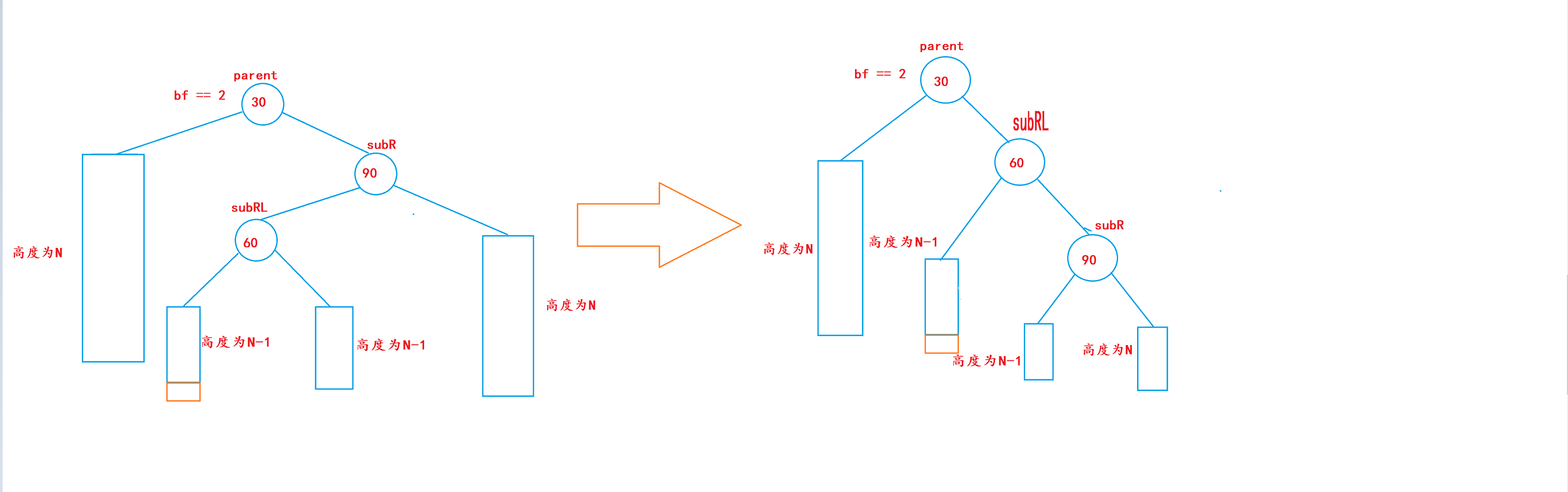
2. 对parent节点进行左单旋
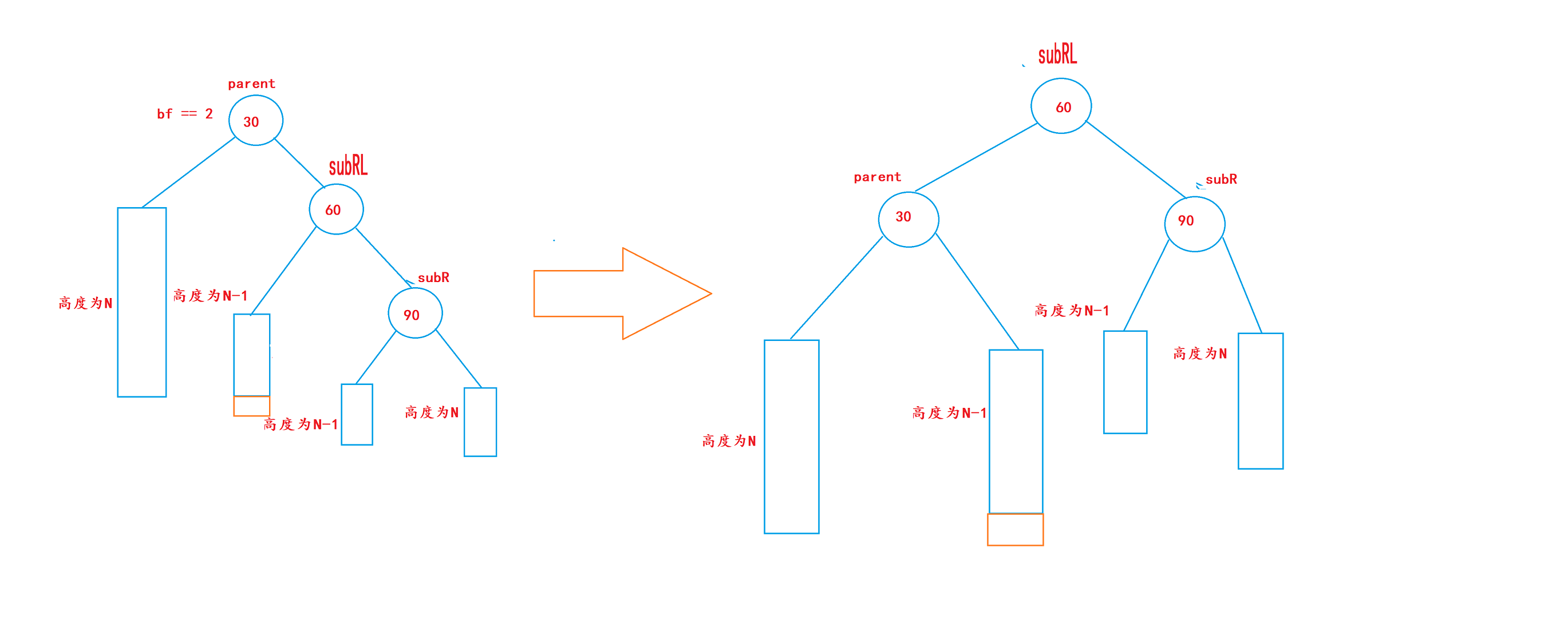
3. 完整步骤
右左双旋后满足二叉搜索树的性质:
右左双旋后,实际上就是让subRL的左子树和右子树,分别作为parent和subR的右子树和左子树,再让parent和subR分别作为subRL的左右子树,最后让subRL作为整个子树的根。
1、subRL的左子树当中的结点本身就比parent的值大,因此可以作为parent的右子树。
2、subRL的右子树当中的结点本身就比subR的值小,因此可以作为subR的左子树。
3、经过步骤1、2后,parent及其子树当中结点的值都就比subRL的值小,而subR及其子树当中结点的值都就比subRL的值大,因此它们可以分别作为subRL的左右子树。
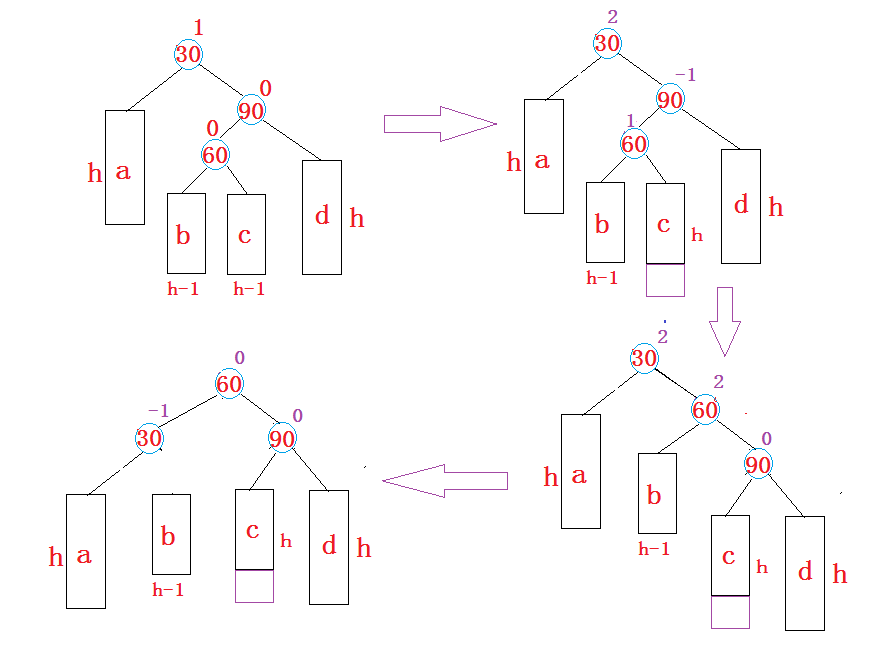
右左双旋后,平衡因子的更新随着subRL原始平衡因子的不同分为以下三种情况:
1、当
subRL原始平衡因子是1时,右左双旋后parent、subR、subRL的平衡因子分别更新为-1、0、0。
2、 当
subRL原始平衡因子是-1时,右左双旋后parent、subR、subRL的平衡因子分别更新为0、1、0
3、当
subRL原始平衡因子是0时,左右双旋后parent、subR、subRL的平衡因子分别更新为0、0、0。
代码如下:
void RotateRL(Node* parent)
{Node* subR = parent->_right;Node* subRL = subR->_left;int bf = subRL->_bf;RotateR(subR);RotateL(parent);if (bf == 1){subR->_bf == 0;parent->_bf = -1;subRL->_bf = 0;}else if (bf == -1){subR->_bf = 1;parent->_bf = 0;subRL->_bf = 0;}else if (bf == 0){subR->_bf = parent->_bf = subRL->_bf = 0;}else {assert(false);}
}
3. AVL的验证
AVL树是在二叉搜索树的基础上加入了平衡性的限制,因此要验证AVL树,可以分两步:
- 验证其为二叉搜索树
- 如果中序遍历可得到一个有序的序列,就说明为二叉搜索树
- 验证其为平衡树
- 每个节点子树高度差的绝对值不超过1(注意节点中如果没有平衡因子)
- 节点的平衡因子是否计算正确
详解代码:
public:void InOrder()
{_InOrder(_root);
}int Size()
{_Size(_root);
}int Height()
{_Height(_root);
}bool IsBalanceTree()
{return _IsBalanceTree(_root);
}private:bool _IsBalanceTree(Node* root)
{if (root == nullptr){return true;}int leftHeight = _Height(root->_left);int rightHeight = _Height(root->_right);// 计算左右子树高度差绝对值int dec = abs(leftHeight - rightHeight);// 如果比1大说明不平衡if (dec > 1){cout << root->_kv.first << endl;return false;}// 检查平衡因子是否计算正确if (rightHeight - leftHeight != root->_bf){cout << root->_kv.first << endl;return false;}return _IsBalanceTree(root->_left) && _IsBalanceTree(root->_right);
}
int _Height(Node* root)
{if (root == nullptr){return 0;}int leftHeight = _Height(root->_left);int rightHeight = _Height(root->_right);return max(leftHeight, rightHeight) + 1;
}int _Size(Node* root)
{if (root == nullptr){return 0;}return _Size(root->_left) + _Size(root->_right) + 1;
}void _InOrder(Node* root)
{if (root == nullptr){return;}_InOrder(root->_left);cout << root->_kv.first << ":" << root->_kv.second << endl;_InOrder(root->_right);
}
3. AVL的验证
⚡验证示例1
int a[] = {16, 3, 7, 11, 9, 26, 18, 14, 15};
验证代码:
void AVLTest1()
{AVLTree<int, int> t;int a[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };for (auto& e : a){t.Insert({ e,e });cout << "Insert:" << e << "->" << t.IsBalanceTree() << endl;}t.InOrder();
}
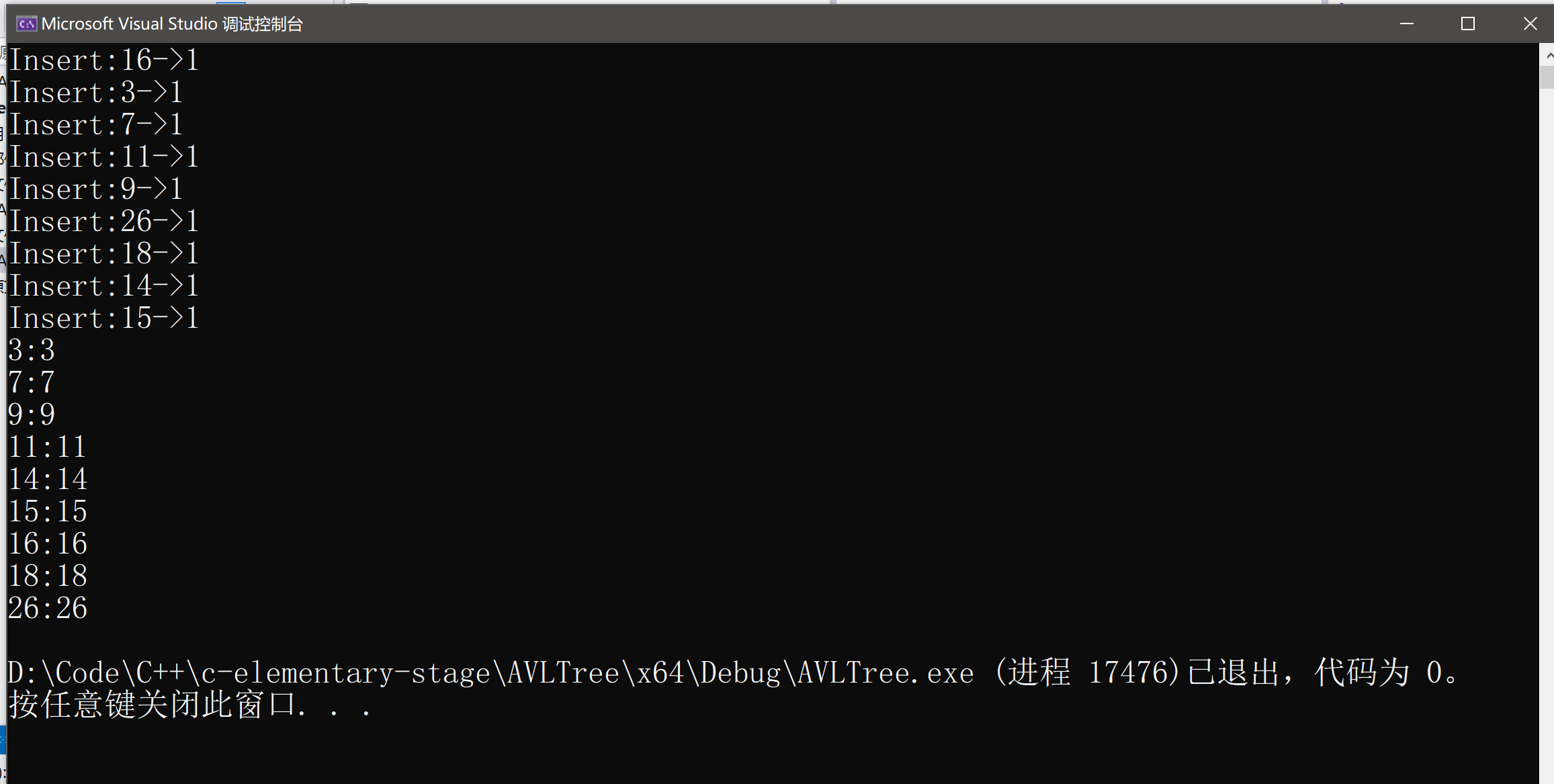
⚡验证示例2
int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };
验证代码:
void AVLTest1()
{AVLTree<int, int> t;int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };for (auto& e : a){t.Insert({ e,e });cout << "Insert:" << e << "->" << t.IsBalanceTree() << endl;}t.InOrder();
}
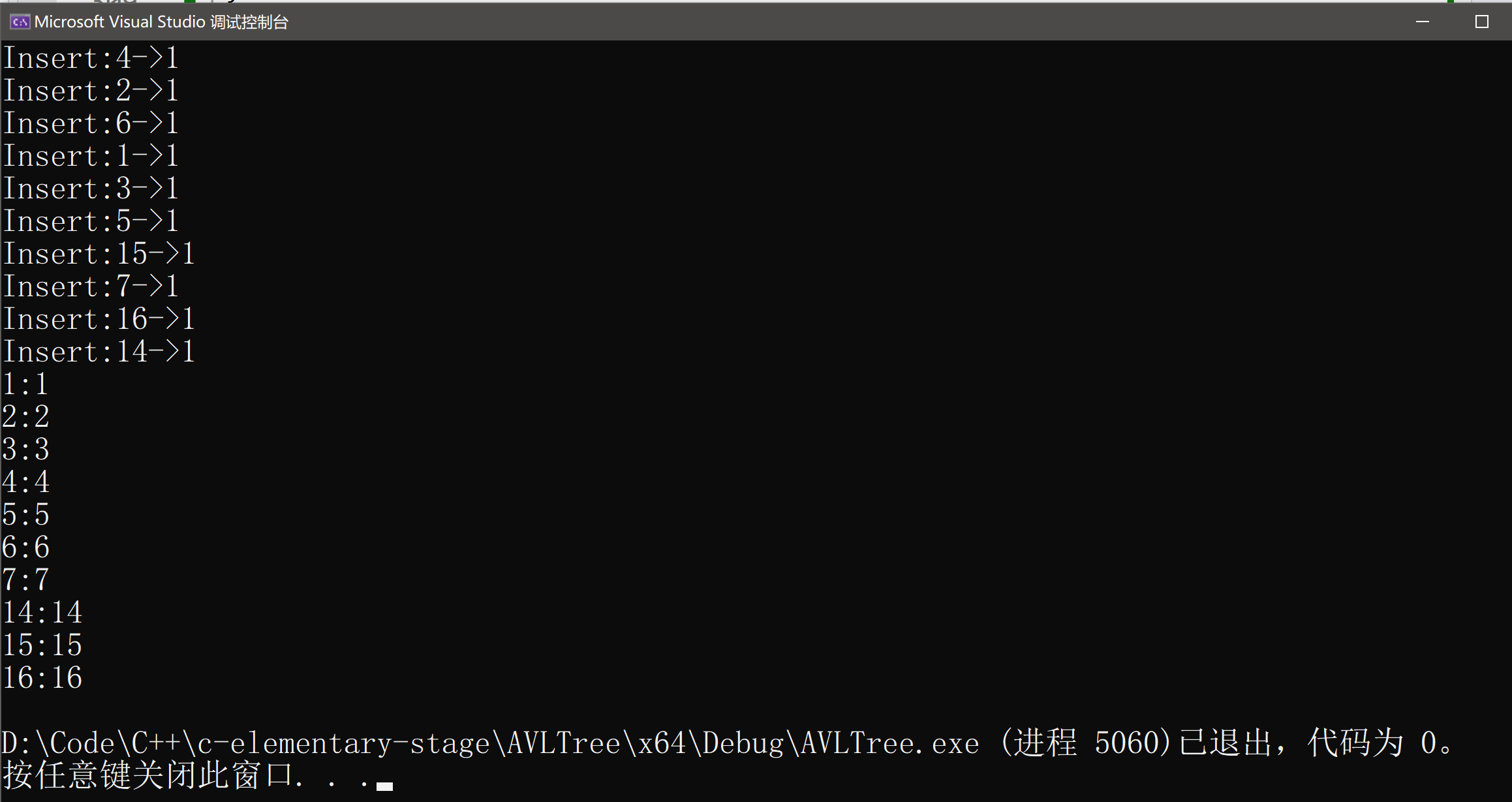
3. AVL的性能
AVL树是一棵绝对平衡的二叉搜索树,其要求每个节点的左右子树高度差的绝对值都不超过1,这样可以保证查询时高效的时间复杂度,即 l o g 2 ( N ) log_2 (N) log2(N)。但是如果要对AVL树做一些结构修改的操作,性能非常低下,比如:插入时要维护其绝对平衡,旋转的次数比较多,更差的是在删除时,有可能一直要让旋转持续到根的位置。因此:如果需要一种查询高效且有序的数据结构,而且数据的个数为静态的(即不会改变),可以考虑AVL树,但一个结构经常修改,就不太适合。
相关文章:

【平衡二叉树】AVL树(双旋)
🎉博主首页: 有趣的中国人 🎉专栏首页: C进阶 🎉其它专栏: C初阶 | Linux | 初阶数据结构 小伙伴们大家好,本片文章将会讲解AVL树的左双选和右双旋的相关内容。 如果看到最后您觉得这篇文章写…...

【保姆级介绍自动化的讲解】
🌈个人主页: 程序员不想敲代码啊 🏆CSDN优质创作者,CSDN实力新星,CSDN博客专家 👍点赞⭐评论⭐收藏 🤝希望本文对您有所裨益,如有不足之处,欢迎在评论区提出指正,让我们共…...

【大数据面试题】27 讲下Doris的物化视图
一步一个脚印,一天一道面试题。 物化视图概念 物化视图,顾名思义,是将一个查询的结果预先计算并存储为物理表的形式。这意味着,原本需要在运行时动态执行的复杂查询,现在变成了直接从已经计算好的结果表中读取数据&a…...

kylin 使用心得
Kylin操作系统是一种基于Linux的操作系统,主要在中国使用,由中国国内的开发团队维护。它的目标是为了提供一个稳定、安全、易于使用的操作环境。以下是一些用户可能基于Kylin操作系统的使用心得: 1. **界面友好**:Kylin操作系统通…...
在线音乐系统
文章目录 在线音乐系统一、项目演示二、项目介绍三、部分功能截图四、部分代码展示五、底部获取项目(9.9¥带走) 在线音乐系统 一、项目演示 音乐网站 二、项目介绍 基于springbootvue的前后端分离在线音乐系统 登录角色 : 用户、管理员 用…...

LeetCode算法题:49. 字母异位词分组(Java)
给你一个字符串数组,请你将 字母异位词 组合在一起。可以按任意顺序返回结果列表。 字母异位词 是由重新排列源单词的所有字母得到的一个新单词。 示例 1: 输入: strs ["eat", "tea", "tan", "ate", "nat", …...
第五课,输入函数、布尔类型、比较运算和if判断
一,输入函数input() 与输出函数print()相对应的,是输入函数input(),前者是把程序中的数据展示给外界(比如电脑屏幕上),而后者是把外界(比如键盘)的数据输入进程序中 input()函数可…...
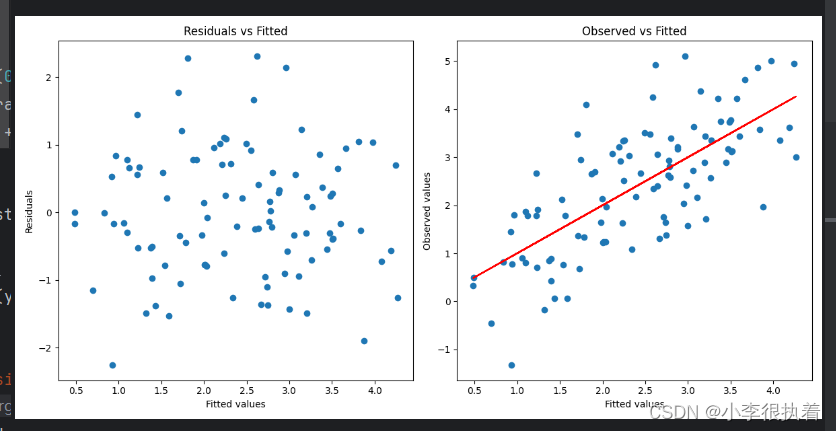
数学建模——线性回归模型
目录 1.线性回归模型的具体步骤和要点: 1.收集数据: 2.探索性数据分析: 3.选择模型: 4.拟合模型: 5.评估模型: 1.R平方(R-squared): 2.调整R平方(Ad…...

景源畅信:抖音小店比较冷门的品类分享?
在抖音小店的世界里,热门品类总是吸引着众多商家和消费者的目光。然而,就像星空中的繁星,虽不那么耀眼却依然存在的冷门品类同样值得我们关注。它们或许不似服装、美妆那样日进斗金,但正是这些小众市场的存在,为平台带…...

java项目之企业资产管理系统(springboot+vue+mysql)
风定落花生,歌声逐流水,大家好我是风歌,混迹在java圈的辛苦码农。今天要和大家聊的是一款基于springboot的企业资产管理系统。项目源码以及部署相关请联系风歌,文末附上联系信息 。 项目简介: 管理员功能有个人中心&…...

[ardunio ide导入blinker库]
1 blinker库下载地址 https://github.com/blinker-iot/blinker-library2 导入方法一 zip导入 项目 -> 导入库 ->添加.zip库 3 导入方法二...

Llama 3 超级课堂 -笔记
课程文档: https://github.com/SmartFlowAI/Llama3-Tutorial 课程视频:https://space.bilibili.com/3546636263360696/channel/series 1 环境配置 1.1 创建虚拟环境,名为:llama3 conda create -n llama3 python3.10 1.2 下载、安装 pyt…...

Leetcode 第 129 场双周赛题解
Leetcode 第 129 场双周赛题解 Leetcode 第 129 场双周赛题解题目1:3127. 构造相同颜色的正方形思路代码复杂度分析 题目2:3128. 直角三角形思路代码复杂度分析 题目3:3129. 找出所有稳定的二进制数组 I思路代码复杂度分析 题目4:…...
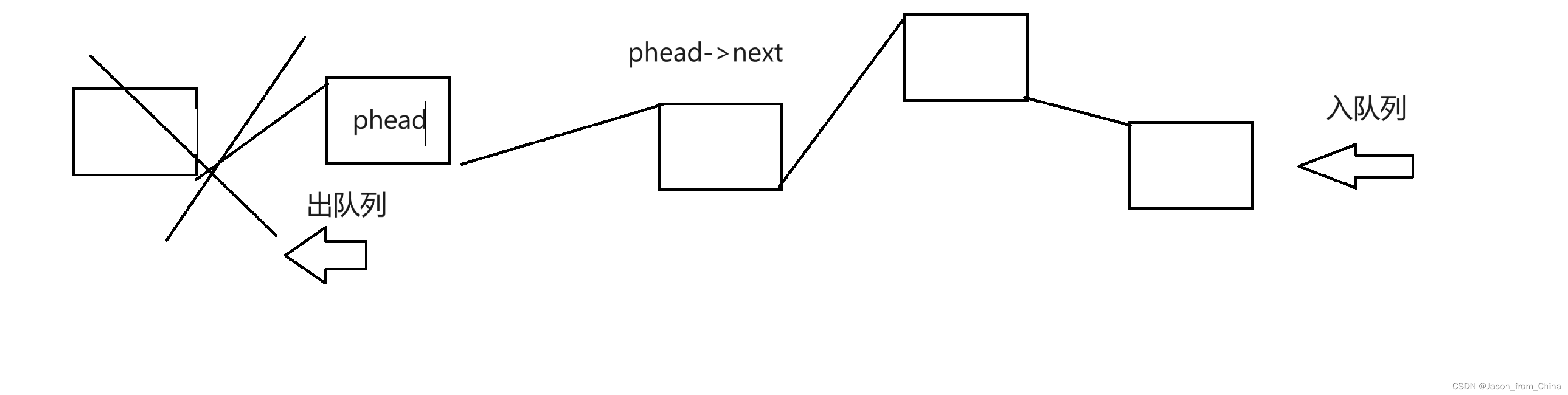
队列的讲解
队列的概念 队列:只允许在一端进行插入数据操作,在另一端进行删除数据操作的特殊线性表,队列具有先进先出FIFO(First In First Out) 入队列:进行插入操作的一端称为队尾 出队列:进行删除操作的一端称为队头 一端进另一端出 也就是可以做到,先…...
)
算法学习笔记(LCA)
L C A LCA LCA:树上两个点的最近公共祖先。(两个节点所有公共祖先中,深度最大的公共祖先) L C A LCA LCA的性质: 在所有公共祖先中, L C A ( x , y ) LCA(x,y) LCA(x,y)到 x x x和 y y y的距离都最短。 x …...

记一次苹果appstore提审拒审问题1.2
有关苹果appstore审核1.2问题的处理方案 2023.8.6苹果回复 Bug Fix Submissions The issues weve identified below are eligible to be resolved on your next update. If this submission includes bug fixes and youd like to have it approved at this time, reply to thi…...
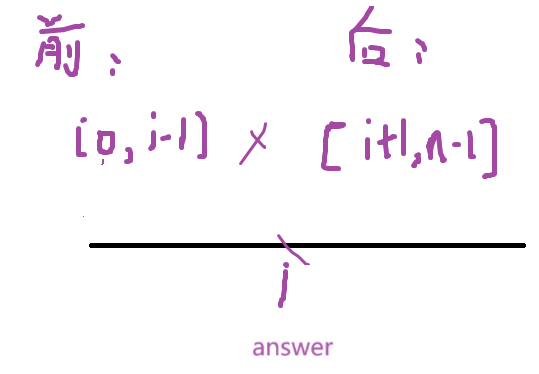
在做题中学习(59):除自身以为数组的乘积
238. 除自身以外数组的乘积 - 力扣(LeetCode) 解法:前缀积和后缀积 思路:answer中的每一个元素都是除自己以外所有元素的和。那就处理一个前缀积数组和后缀积数组。 而前缀积(f[i])是:[0,i-1]所有元素的乘积 后缀…...

centos 把nginx更新到最新版本
yum install epel-release # 添加 EPEL 软件仓库,这是 Nginx 官方软件仓库的依赖项 yum install yum-utils # yum-utils 包含了 yum-config-manager 工具,它可以让您轻松地启用、禁用或配置 yum 软件仓库 vi /etc/yum.repos.d/nginx.repo # 增加以下内容…...
01.认识HTML及常用标签
目录 URL(统一资源定位系统) HTML(超文本标记语言) 1)html标签 2)head标签 3)title标签 4)body标签 标签的分类 DTD文档声明 基础标签 1)H系列标签 2)…...

从零开始:C++ String类的模拟实现
文章目录 引言1.类的基本结构2.构造函数和析构函数3.基本成员函数总结 引言 在C编程中,字符串操作是非常常见且重要的任务。标准库中的std::string类提供了丰富且强大的功能,使得字符串处理变得相对简单。然而,对于学习C的开发者来说&#x…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

JAVA后端开发——多租户
数据隔离是多租户系统中的核心概念,确保一个租户(在这个系统中可能是一个公司或一个独立的客户)的数据对其他租户是不可见的。在 RuoYi 框架(您当前项目所使用的基础框架)中,这通常是通过在数据表中增加一个…...

逻辑回归暴力训练预测金融欺诈
简述 「使用逻辑回归暴力预测金融欺诈,并不断增加特征维度持续测试」的做法,体现了一种逐步建模与迭代验证的实验思路,在金融欺诈检测中非常有价值,本文作为一篇回顾性记录了早年间公司给某行做反欺诈预测用到的技术和思路。百度…...

在 Spring Boot 中使用 JSP
jsp? 好多年没用了。重新整一下 还费了点时间,记录一下。 项目结构: pom: <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http://ww…...

数学建模-滑翔伞伞翼面积的设计,运动状态计算和优化 !
我们考虑滑翔伞的伞翼面积设计问题以及运动状态描述。滑翔伞的性能主要取决于伞翼面积、气动特性以及飞行员的重量。我们的目标是建立数学模型来描述滑翔伞的运动状态,并优化伞翼面积的设计。 一、问题分析 滑翔伞在飞行过程中受到重力、升力和阻力的作用。升力和阻力与伞翼面…...
基础)
6个月Python学习计划 Day 16 - 面向对象编程(OOP)基础
第三周 Day 3 🎯 今日目标 理解类(class)和对象(object)的关系学会定义类的属性、方法和构造函数(init)掌握对象的创建与使用初识封装、继承和多态的基本概念(预告) &a…...

高防服务器价格高原因分析
高防服务器的价格较高,主要是由于其特殊的防御机制、硬件配置、运营维护等多方面的综合成本。以下从技术、资源和服务三个维度详细解析高防服务器昂贵的原因: 一、硬件与技术投入 大带宽需求 DDoS攻击通过占用大量带宽资源瘫痪目标服务器,因此…...