Java bin目录中的文件如何执行?
在 Java 项目中,bin 目录通常用于存放编译后的 .class 文件。如果你将编译后的 .class 文件放在 bin 目录中,需要确保在运行 Java 程序时指定正确的类路径。下面是一个简单的例子说明如何执行 bin 目录中的文件。
假设你的项目结构如下:
project/
├── src/
│ └── com/
│ └── example/
│ └── MainClass.java
└── bin/└── com/└── example/└── MainClass.class
其中,MainClass.java 文件内容如下:
package com.example;public class MainClass {public static void main(String[] args) {System.out.println("Hello, World!");}
}
编译步骤
-
编译 Java 源文件到
bin目录:
你需要使用-d选项来指定编译后的输出目录。执行以下命令将源文件编译到bin目录:javac -d bin src/com/example/MainClass.java -
检查
bin目录:
确保bin目录中有正确的文件结构和编译后的.class文件:bin/ └── com/└── example/└── MainClass.class
运行步骤
- 运行 Java 程序:
使用-cp(类路径)选项指定bin目录,并运行主类。注意,你需要使用类的全限定名(即包名 + 类名)来运行程序:java -cp bin com.example.MainClass
详细示例
完整示例如下:
-
创建项目目录结构:
mkdir -p project/src/com/example mkdir -p project/bin -
创建 Java 源文件:
创建文件project/src/com/example/MainClass.java,并写入以下代码:package com.example;public class MainClass {public static void main(String[] args) {System.out.println("Hello, World!");} } -
编译 Java 源文件:
javac -d project/bin project/src/com/example/MainClass.java -
运行 Java 程序:
cd project java -cp bin com.example.MainClass
这样,你应该会看到输出:
Hello, World!
确保你在运行时指定的类路径(-cp bin)和类的全限定名(com.example.MainClass)正确无误,这样就能成功执行 bin 目录中的文件。
相关文章:

Java bin目录中的文件如何执行?
在 Java 项目中,bin 目录通常用于存放编译后的 .class 文件。如果你将编译后的 .class 文件放在 bin 目录中,需要确保在运行 Java 程序时指定正确的类路径。下面是一个简单的例子说明如何执行 bin 目录中的文件。 假设你的项目结构如下: pr…...
Kafka和Spark Streaming的组合使用学习笔记(Spark 3.5.1)
一、安装Kafka 1.执行以下命令完成Kafka的安装: cd ~ //默认压缩包放在根目录 sudo tar -zxf kafka_2.12-2.6.0.tgz -C /usr/local cd /usr/local sudo mv kafka_2.12-2.6.0 kafka-2.6.0 sudo chown -R qiangzi ./kafka-2.6.0 二、启动Kafaka 1.首先需要启动K…...
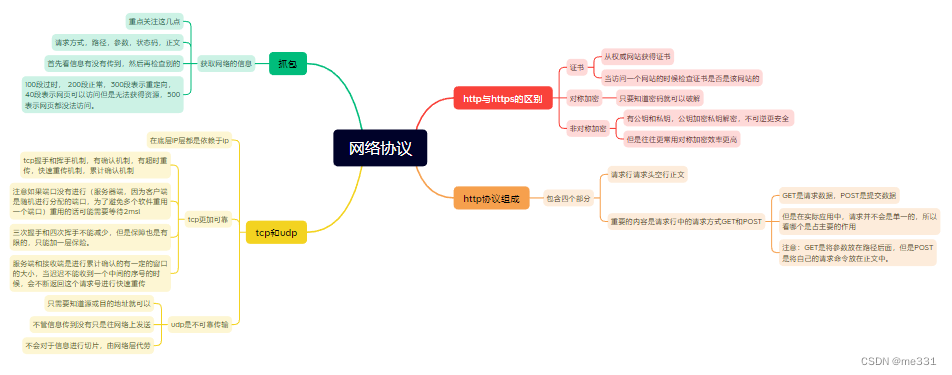
5.9网络协议
由网卡发送数据通过网线进行发送,当网卡接收到信号以后将数据传给内核数据区,然后由操作系统交给相应的进程。 将数据进行发送的时候需要借助于网线实现,这个时候会出现当传输的数据比较远的时候就借助于中继器将信号进行再生扩大࿰…...

QT客户端开发的注意事项
QT客户端开发是一个涉及图形用户界面(GUI)设计、网络编程、数据库交互等多个方面的复杂过程。以下是在进行QT客户端开发时应注意的一些关键事项,通过关注这些事项,可以提高QT客户端应用的质量和开发效率。北京木奇移动技术有限公司…...

k8s源码编译失败:Makefile:1: *** 缺失分隔符。 停止。
目录 问题解决 更换Arch或系统 问题解决 编译k8s源码的kubelet时执行make失败:Makefile:1: *** 缺失分隔符。 停止。 首先,查看文件内容 # cat Makefile build/root/Makefile 修改Makefile,给第一行前增加include,如下&…...

服务器数据恢复—拯救raid5阵列数据行动,raid5数据恢复案例分享
Raid5数据恢复算法原理: 分布式奇偶校验的独立磁盘结构(被称之为raid5)的数据恢复有一个“奇偶校验”的概念。可以简单的理解为二进制运算中的“异或运算”,通常使用的标识是xor。运算规则:若二者值相同则结果为0&…...

旅游集市数仓建设
旅游集市数仓建设 小白如何从0到1成为大数据工程师 目录 旅游集市数仓建设 1.上传数据 2.可能用到的UDF函数 3.创建所需数据库及表 1)ODS层 ①ods_oidd ②ods_wcdr ③ods_ddr ④ods_dpi 2)DWD层 ①dwd_res_regn_mergelocation_msk_d ②dwm_s…...

vue实现点击高亮效果
<view class"tabs"><textv-for"(item, index) in subTypes":key"item.id"class"text":class"{ active: index activeIndex }"//动态绑定高亮类:判断下标是否等于当前下标tap"activeIndex index&…...
uniapp 配置请求代理+请求封装
uniapp官网提供了三种方式:什么是跨域 | uni-app官网 1. 通过uniapp自带浏览器 打开项目是不存在跨域的 第二种方式: "h5" : {"template" : "static/index.html","devServer": {"proxy": {&quo…...

代码随想录算法训练营第二十八天|216.组合总和III、17.电话号码的字母组合
216.组合总和III 文档讲解:代码随想录 题目链接:. - 力扣(LeetCode) 这一题与昨天的组合差不多,区别就在只有和是目标值的时候才会加入到result数组中,并且在回溯时,会处理sum的值 class Solution:def __i…...
大模型prompt实例:知识库信息质量校验模块
大模型相关目录 大模型,包括部署微调prompt/Agent应用开发、知识库增强、数据库增强、知识图谱增强、自然语言处理、多模态等大模型应用开发内容 从0起步,扬帆起航。 大模型应用向开发路径:AI代理工作流大模型应用开发实用开源项目汇总大模…...

正则表达式和lambda表达式
正则表达式(Regular Expressions)和Lambda表达式虽然都包含“表达式”一词,但它们在编程中的作用和用法是完全不同的。让我们详细比较一下它们的定义、用途和应用场景: 正则表达式 定义:正则表达式是一种用于匹配文本…...
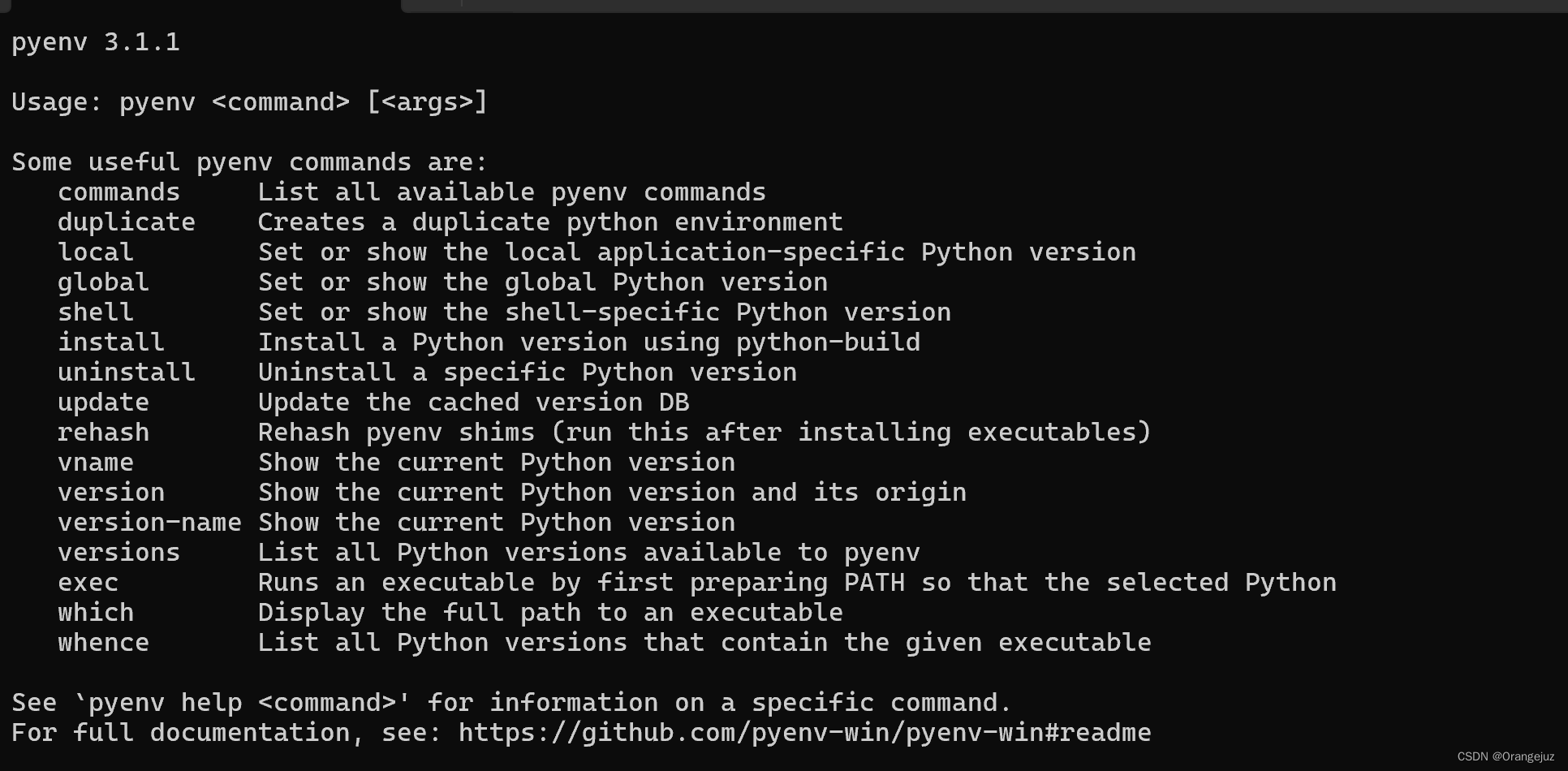
pyenv 之 python 多版本管理(win11)
1. 背景 常常会用到Python的多个版本,因此可以使用Pyenv来对Python版本进行管理。 2. win11下载 pyenv 在终端执行下载语句: pip install pyenv-win --target D:\software\pyenv 其中 D:\software\pyenv 为你想要下载到的文件目录,建议在 …...

nodemon运行ts文件
https://juejin.cn/post/7035637086451400734 nodemon经常用来调试js文件,大家都是知道的,但是用nodemon来调试ts文件,大家试过吗? 如果直接运行nodemon index.ts是会报错的。 ts 复制代码 //index.ts console.log(1) 需要全局…...

内网渗透瑞士军刀-impacket工具解析(二)
impacket工具解析之Kerberos认证协议 上一期我们介绍了impacket中ntlm协议的实现,在Windows认证中除了使用ntlm认证,还支持Kerberos认证协议,Kerberos认证也是Windows 活动目录中占比最高的认证方式。 什么是Kerberos协议? Kerb…...

huggingface 笔记:pipeline
1 介绍 pipeline() 是使用预训练模型进行推理的最简单和最快速的方式。可以针对不同模态的许多任务直接使用 pipeline() 2 举例:情感分析 2.1 创建pipeline实例 from transformers import pipelineclassifier pipeline("sentiment-analysis") #首先创…...
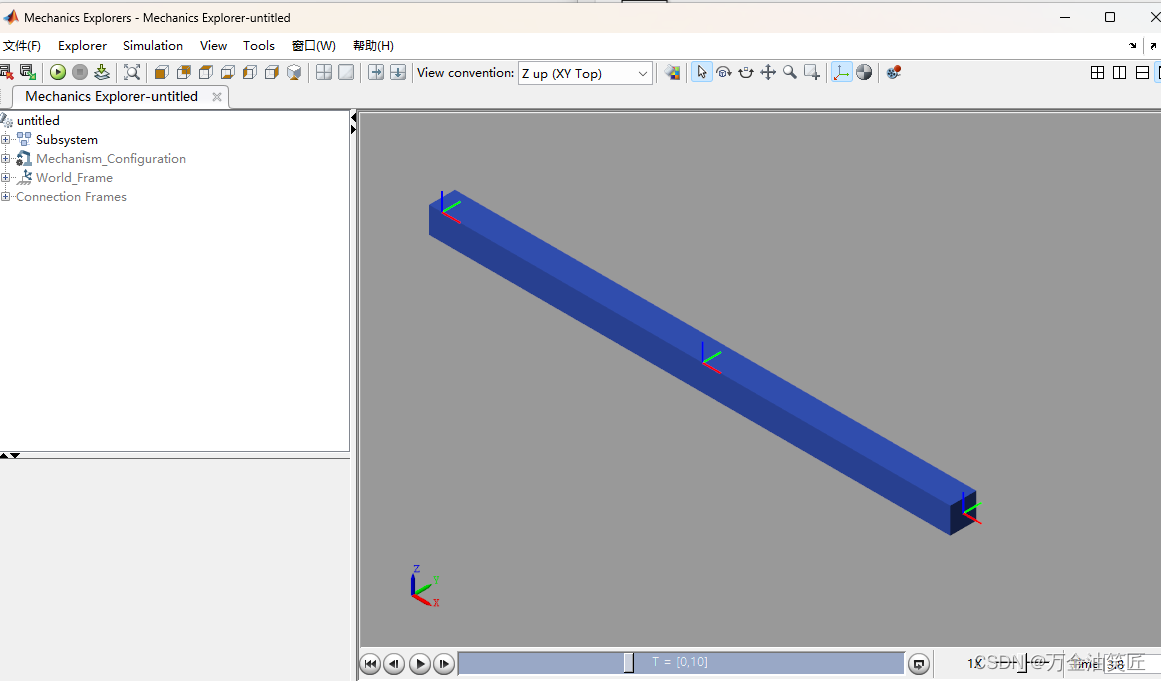
玩转Matlab-Simscape(初级)-01-从一个简单模型开始学习之旅
** 玩转Matlab-Simscape(初级)- 01 - 从一个简单模型开始学习之旅 ** 目录 玩转Matlab-Simscape(初级)- 01 - 从一个简单模型开始学习之旅 前言一、从模板开始建模二、建模一个简单的连杆2.1 建模2.2 生成子系统 总结 前言 在产…...
电脑录屏软件有哪些?这3款神器必须要知道
在当今现代社会,电脑录屏软件已经成为人们日常生活中不可或缺的一部分。无论是录制游戏精彩瞬间、制作教程、还是在线会议记录,一款好用的电脑录屏软件都能帮助我们更高效地完成任务。可是电脑录屏软件有哪些呢?接下来,我们将介绍…...
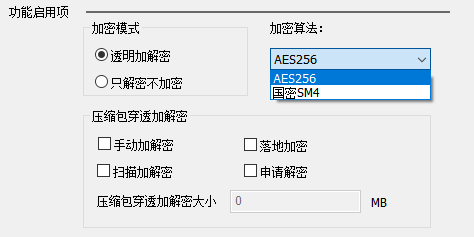
如何在华企盾DSC防泄密系统中设置文件自动加密?
在华企盾DSC系统中设置文件自动加密的过程,简单且用户友好,确保了企业数据的安全,同时不干扰日常工作流程。以下是设置文件自动加密的步骤: 系统安装与配置:确保华企盾DSC数据防泄密系统已经在企业的网络中正确安装和配…...

【DevOps】Dockerfile详解,做自己的docker镜像
学会使用DockerHub找自己想要的镜像以后,我们会很方便的使用一些公用镜像仓库的Docker镜像。但是开发和部署的过程中,能找到的镜像可能并不能满足我们需要,这样我们就需要自己制作Docker镜像。我们通过需要编写一个 Dockerfile,然…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...
详细解析)
Caliper 负载(Workload)详细解析
Caliper 负载(Workload)详细解析 负载(Workload)是 Caliper 性能测试的核心部分,它定义了测试期间要执行的具体合约调用行为和交易模式。下面我将全面深入地讲解负载的各个方面。 一、负载模块基本结构 一个典型的负载模块(如 workload.js)包含以下基本结构: use strict;/…...

消息队列系统设计与实践全解析
文章目录 🚀 消息队列系统设计与实践全解析🔍 一、消息队列选型1.1 业务场景匹配矩阵1.2 吞吐量/延迟/可靠性权衡💡 权衡决策框架 1.3 运维复杂度评估🔧 运维成本降低策略 🏗️ 二、典型架构设计2.1 分布式事务最终一致…...

深入浅出WebGL:在浏览器中解锁3D世界的魔法钥匙
WebGL:在浏览器中解锁3D世界的魔法钥匙 引言:网页的边界正在消失 在数字化浪潮的推动下,网页早已不再是静态信息的展示窗口。如今,我们可以在浏览器中体验逼真的3D游戏、交互式数据可视化、虚拟实验室,甚至沉浸式的V…...

用神经网络读懂你的“心情”:揭秘情绪识别系统背后的AI魔法
用神经网络读懂你的“心情”:揭秘情绪识别系统背后的AI魔法 大家好,我是Echo_Wish。最近刷短视频、看直播,有没有发现,越来越多的应用都开始“懂你”了——它们能感知你的情绪,推荐更合适的内容,甚至帮客服识别用户情绪,提升服务体验。这背后,神经网络在悄悄发力,撑起…...

结构化文件管理实战:实现目录自动创建与归类
手动操作容易因疲劳或疏忽导致命名错误、路径混乱等问题,进而引发后续程序异常。使用工具进行标准化操作,能有效降低出错概率。 需要快速整理大量文件的技术用户而言,这款工具提供了一种轻便高效的解决方案。程序体积仅有 156KB,…...
