小丑的身份证和复印件 (BFS + Floyd)
本题链接:登录—专业IT笔试面试备考平台_牛客网
题目:

样例:
|
| 12 |
思路:
根据题意,要求最短时间,实际上也可以理解为最短距离。
所以应该联想到有关最短距离的算法,在这里给出的 n,m是100,所以我们可以暴力求最短距离即可,身份碎片虽然分大小写,但是它们都是唯一的点,所以可以通过Floyd,记录每个点之间的最短距离,随后累加即可,其次这里的最短距离可以用BFS求得最短距离。注意一个细节,初始化无穷大的时候,尽量小一些,否则多个INF累加爆 long long 就会答案错误。
代码详解如下:
#include <iostream>
#include <vector>
#include <queue>
#include <climits>
#include <algorithm>
#define endl '\n'
#define int long long
#define x first
#define y second
#define umap unordered_map
#define All(x) x.begin(),x.end()
#pragma GCC optimize(3,"Ofast","inline")
#define IOS std::ios::sync_with_stdio(false),cin.tie(0), cout.tie(0)
using namespace std;
const int N = 2e6 + 10;
inline void solve();signed main()
{
// freopen("a.txt", "r", stdin);IOS;int _t = 1;// cin >> _t;while (_t--){solve();}return 0;
}
using PII = pair<int,int>;
int n,m;
PII rem[256]; // rem 记录最短路中字符的位置
char g[110][110];int dist[256][256]; // Floyd最短距离int dx[] = {0,1,0,-1};
int dy[] = {1,0,-1,0};
// BFS 求字符a 到字符 b 之间的最短路
inline int Dist(char a,char b)
{// 标记是否走动过当前位置vector<vector<bool>>st(110,vector<bool>(110,false));// 判断是否可以走动的条件auto isRun = [&](int x,int y)->bool{return (x >= 0 and x < n and y >= 0 and y < m and !st[x][y] and g[x][y] != '#');};// BFS 求最短路int step = 0;queue<PII>q;q.emplace(rem[a]);while(q.size()){int sz = q.size();while(sz--){PII now = q.front();q.pop();if(g[now.x][now.y] == b){rem[b] = now; // 记录当前最短路的位置return step;}st[now.x][now.y] = true;for(int i = 0;i < 4;++i){int bx = now.x + dx[i];int by = now.y + dy[i];if(isRun(bx,by)){st[bx][by] = true;q.emplace(PII(bx,by));}}}++step;}// 返回无穷大return INT_MAX;
}inline void solve()
{// 拿取碎片的方案vector<char>plan = {'J','O','K','E','R','j','o','k','e','r'};cin >> n >> m;for(int i = 0;i < n;++i){for(int j = 0;j < m;++j){char c;cin >> c;g[i][j] = c;// 存储好起点和终点的位置if(c == '(') rem[c] = PII(i,j);if(c == ')') rem[c] = PII(i,j);}}// 存储起点到各个字符之间的最短距离for(char &p:plan) dist['('][p] = Dist('(',p);// 存储终点到各个字符之间的最短距离for(char &p:plan) dist[p][')'] = Dist(')',p);// 存储各个点之间的最短距离for(char &st:plan){for(char &ed:plan){if(st == ed) continue;dist[st][ed] = Dist(st,ed);}}sort(All(plan));// 全排列遍历所有的捡碎片方案// 获取最小的一种答案即可int ans = INT_MAX;do{int res = 0;res += dist['('][*plan.begin()]; //累加起点开始的最短距离for(int i = 1;i < 10;++i) res += dist[plan[i - 1]][plan[i]]; // 按顺序累加最短距离res += dist[plan.back()][')']; // 累加最后到终点最短距离ans = min(ans,res);}while(next_permutation(All(plan)));if(ans >= INT_MAX) cout << "-1" << endl;else cout << ans << endl;
}最后提交:
相关文章:

小丑的身份证和复印件 (BFS + Floyd)
本题链接:登录—专业IT笔试面试备考平台_牛客网 题目: 样例: 输入 2 10 (JOKERjoke #####asdr) 输出 12 思路: 根据题意,要求最短时间,实际上也可以理解为最短距离。 所以应该联想到有关最短距离的算法&…...

C++类与对象(上)
C类与对象 面向过程和面向对象初步认识类的引入类的定义类的两种定义方式: 类的访问限定符及封装访问限定符 封装类的作用域类的实例化类对象模型如何计算类对象的大小结构体内存对齐规则: this指针 面向过程和面向对象初步认识 C语言是面向过程的&…...

Exchanger的 常用场景及使用示例
Exchanger的 常用场景及使用示例 Exchanger是Java并发包中的一个工具类,它用于两个线程之间交换数据。当两个线程都到达同步点并调用exchange()方法时,它们会交换数据然后继续执行。Exchanger特别适用于那些需要两个线程进行协作,交换数据或…...
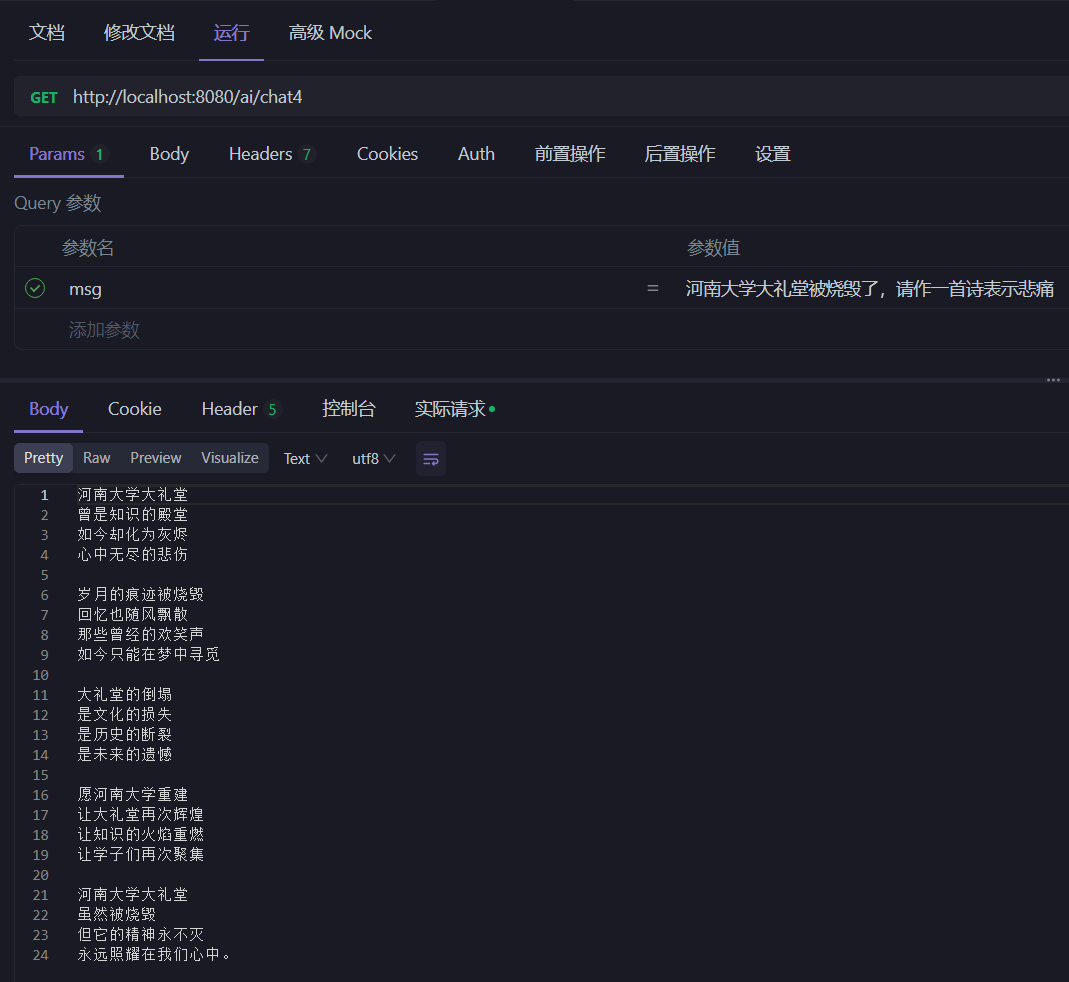
Spring AI项目Open AI对话接口开发指导
文章目录 创建Spring AI项目配置项目pom、application文件controller接口开发接口测试 创建Spring AI项目 打开IDEA创建一个新的spring boot项目,填写项目名称和位置,类型选择maven,组、工件、软件包名称可以自定义,JDK选择17即可…...
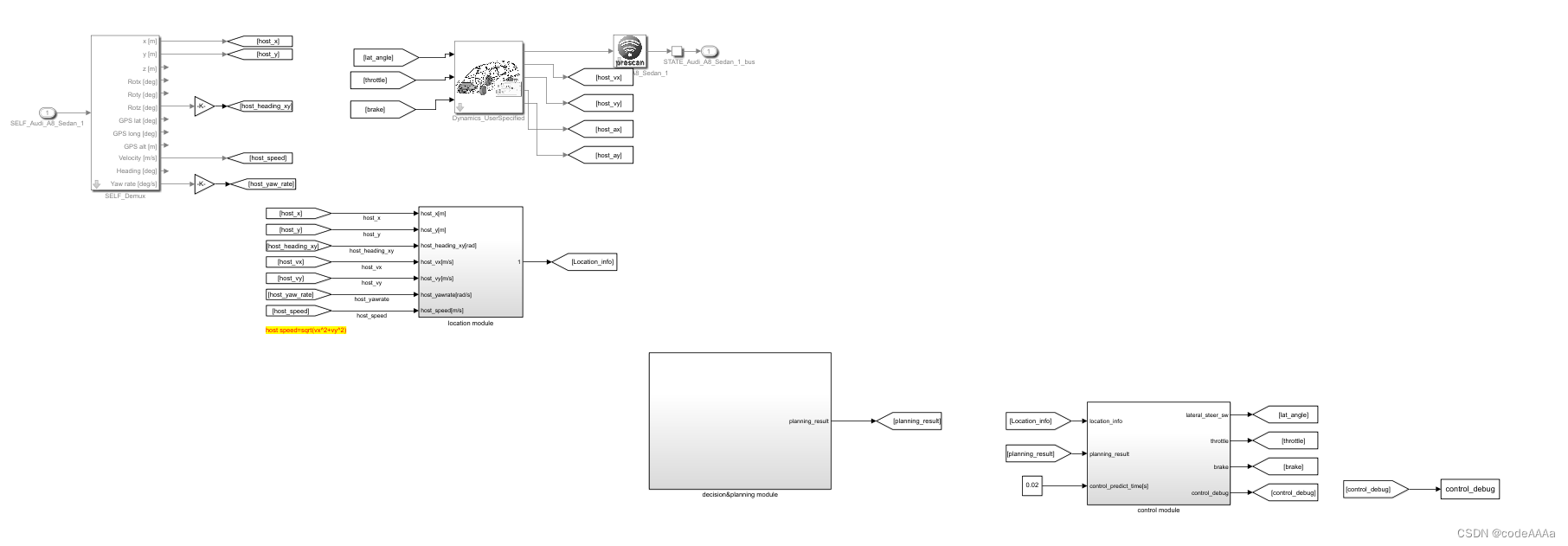
决策规划仿真平台的搭建
以下内容笔记据来自于b站up主忠厚老实的老王,视频;链接如下: 自动驾驶决策规划算法第二章第一节 决策规划仿真平台搭建_哔哩哔哩_bilibili 使用到的软件有matlab、prescan、carsim以及visual stadio。 我电脑上软件的版本是matlab2022a&am…...
之扩展小部件(十八):如何使用badge部件来凸显UI元素?)
RustGUI学习(iced/iced_aw)之扩展小部件(十八):如何使用badge部件来凸显UI元素?
前言 本专栏是学习Rust的GUI库iced的合集,将介绍iced涉及的各个小部件分别介绍,最后会汇总为一个总的程序。 iced是RustGUI中比较强大的一个,目前处于发展中(即版本可能会改变),本专栏基于版本0.12.1. 概述 这是本专栏的第十八篇,主要讲述badge标记部件的使用,会结合实…...
触摸播放视频,并用iframe实现播放外站视频
效果: html: <div:style"{ height: homedivh }"class"rightOne_content_div_div"mouseenter"divSeenter(i)"mouseleave"divLeave(i)"click"ItemClick(i)"><!-- isUser是否是用户上传 --><divv-if…...

接口自动化-requests库
requests库是用来发送请求的库,本篇用来讲解requests库的基本使用。 1.安装requests库 pip install requests 2.requests库底层方法的调用逻辑 (1)get / post / put / delete 四种方法底层调用 request方法 注意:data和json都…...
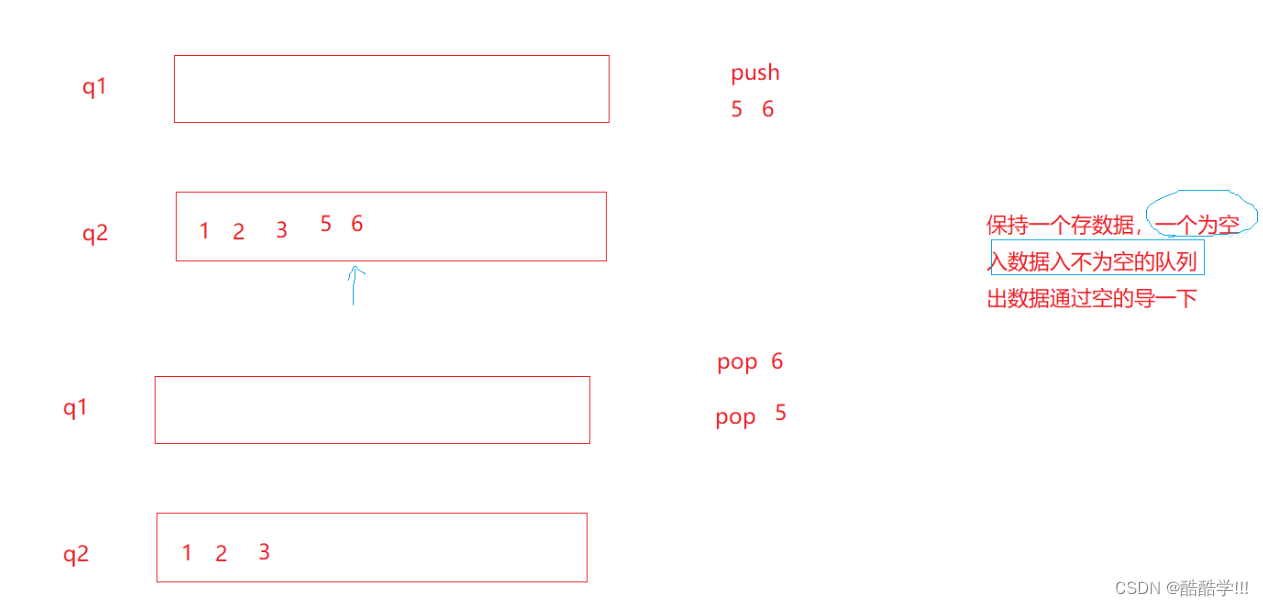
队列的实现与OJ题目解析
"不是你变优秀了, 那个人就会喜欢你." 文章索引 前言1. 什么是队列2. 队列的实现3. OJ题目解析4. 总结 前言 感情可以培养是个伪命题. 如果有足够多的时间和爱, 就可以让另一个人爱上你的话, 那谁和谁都可以相爱了. 爱情之所以会让人死去活来, 是因为, 答案都写在了…...

中北大学软件学院javaweb实验三JSP+JDBC综合实训(一)__数据库记录的增加、查询
目录 1.实验名称2.实验目的3.实验内容4.实验原理或流程图5.实验过程或源代码(一)编程实现用户的登录与注册功能【步骤1】建立数据库db_news2024和用户表(笔者使用的数据库软件是navicat)【步骤2】实现用户注册登录功能(与上一实验报告不同的是࿰…...

高通QCS6490开发(一): 广翼智联FV01 AI板卡简介
《高通QCS6490开发》是一系列AIoT应用开发文章,我们将会在系列文章中陆续介绍基于QCS6490平台上的AIoT应用开发,在文章中,我们选择了广翼智联(FAIOT)公司的FV01产品作为开发板,介绍如何从底层的硬件板卡接线…...
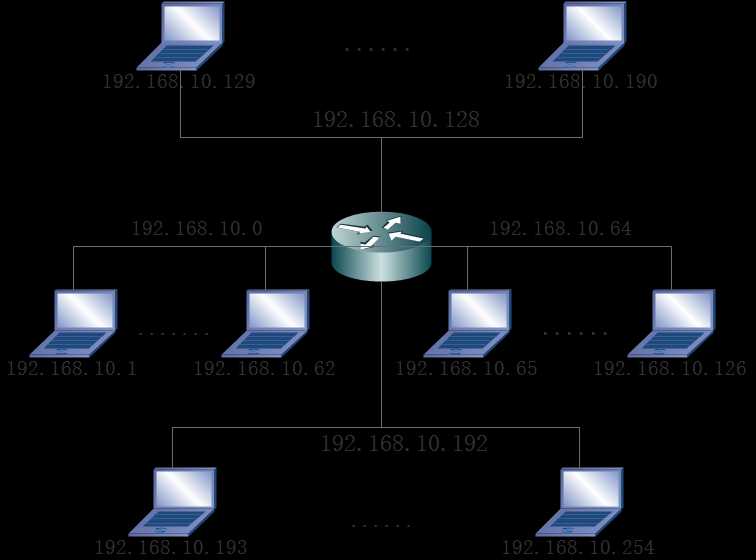
【知识拓展】大白话说清楚:IP地址、子网掩码、网关、DNS等
前言 工作中常听别人说的本地网络是什么意思?同一网段又是什么意思?它俩有关系吗? 在工作中内经常会遇到相关的网络问题,涉及网络通信中一些常见的词汇,如IP地址、子网掩码、网关和DNS等。具体一点:经常会…...

Java 高级面试问题及答案2
Java 高级面试问题及答案 问题 1: 请解释 Java 中的多线程和并发的区别,并举例说明如何避免常见的并发问题。 答案: 多线程是指程序中有多个线程同时执行,而并发是指程序设计中允许多个操作看起来是同时执行的,即使它们可能不是…...
2024年网络安全威胁
随着2024年的到来,数字世界的版图正在以前所未有的速度扩张,引领我们进入一个技术革新的新时代。然而,这飞速的发展同时也催生了一系列错综复杂的网络安全挑战。在这个数字平台与我们生活日益紧密交织的时代,深入了解这些新兴的威…...
应用层之 HTTP 协议
HTTP 协议 HTTP (全称为 "超文本传输协议") 是一种应用非常广泛的 应用层协议。所谓 "超文本" 的含义, 就是传输的内容不仅仅是文本(比如 html, css 这个就是文本), 还可以是一些 其他的资源, 比如图片, 视频, 音频等二进制的数据。浏览器获取到网页&#…...
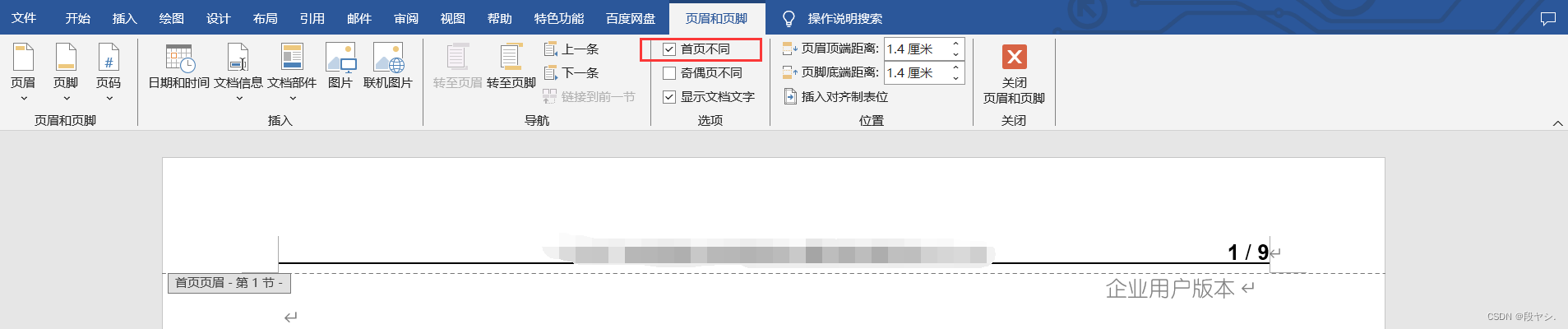
解决Word文档中页眉有部分有,有部分没有的问题
问题描述:一个Word文档中,在页眉上添加文档名称和页码,但是有的有,有的没有,选择“链接到前一节”也无法解决该问题。 原因分析:页眉页脚中,勾选了“首页不同”的选项,如下图&#…...
Python爬虫基础知识学习(以爬取某二手房数据、某博数据与某红薯(书)评论数据为例)
一、爬虫基础流程 爬虫的过程模块化,基本上可以归纳为以下几个步骤: 1、分析网页URL:打开你想要爬取数据的网站,然后寻找真实的页面数据URL地址; 2、请求网页数据:模拟请求网页数据,这里我们介…...
JavaScript-输入输出语句
输出语句 document.write( 输出的内容 ) 语法:document.write( 输出的内容) 作用:内容会显示在网页上 如果输出的内容是标签,也会被解析为网页元素 代码: <!DOCTYPE html> <html lang"en"> <head>&…...

peft+llama3训练自定义数据
要微调自己的模型训练 LLaMA 3,则需要准备一个 JSON 格式的数据集,其中每个条目包含输入文本和相应的标签(如果有的话)。以下是一个 JSON 数据集的示例格式: [{"input": "这是一个输入样本。",&q…...
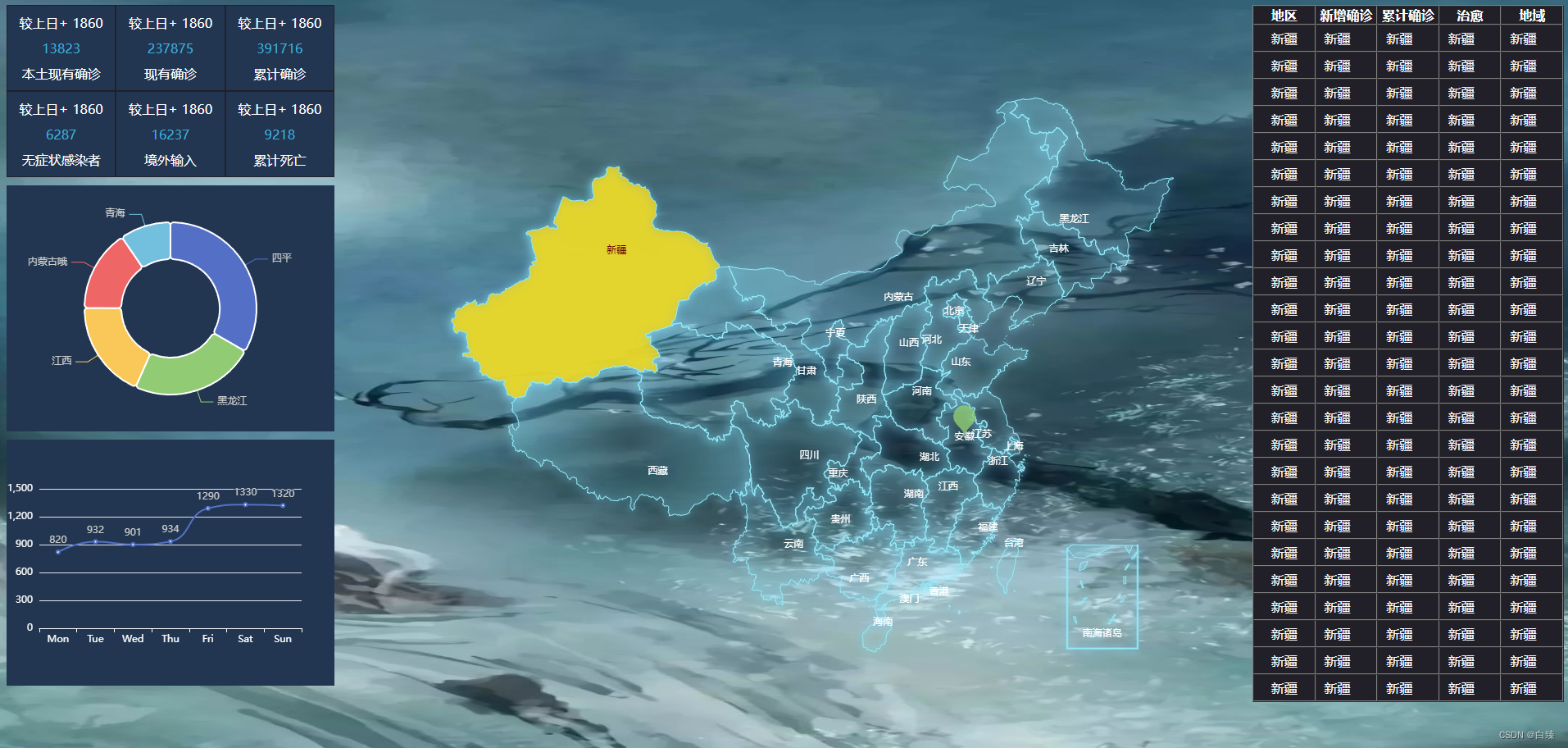
vue+ts+vite+pinia+less+echarts 前端可视化 实战项目
1.初始化前端 输入 npm init vuelatest 命令 然后 选择需要的插件2.构建完成后 在终端切换到vue-project文件夹下 npm install 下载依赖 3.下载 less样式 npm install less less-loader -D 4.下载axios npm install axios 5.下载echarts npm install echarts -S 6.引入中国…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...
