【数据结构】堆(超详细)
文章目录
- 前言
- 堆的概念及结构
- 堆的实现
- 堆的向下调整算法(建小堆为例)
- 堆的向上调整算法(建小堆为例)
- 堆的初始化
- 销毁堆
- 堆的插入
- 堆的删除(规定删堆顶的数据)
- 取堆顶元素
- 判断堆是否为空
- 获取堆的个数
- 完整代码(包括测试代码)
- Heap.h
- Heap.c
- test.c
前言
普通的二叉树是不适合用数组来存储的,因为可能会存在大量的空间浪费。而完全二叉树更适合使用顺序结构存储。在现实中我们通常把堆 (一种完全二叉树) 使用顺序结构的数组来存储,需要注意的是这里的堆和操作系统虚拟进程地址空间中的堆是两回事,一个是数据结构,一个是操作系统中管理内存的一块区域分段。
堆的概念及结构

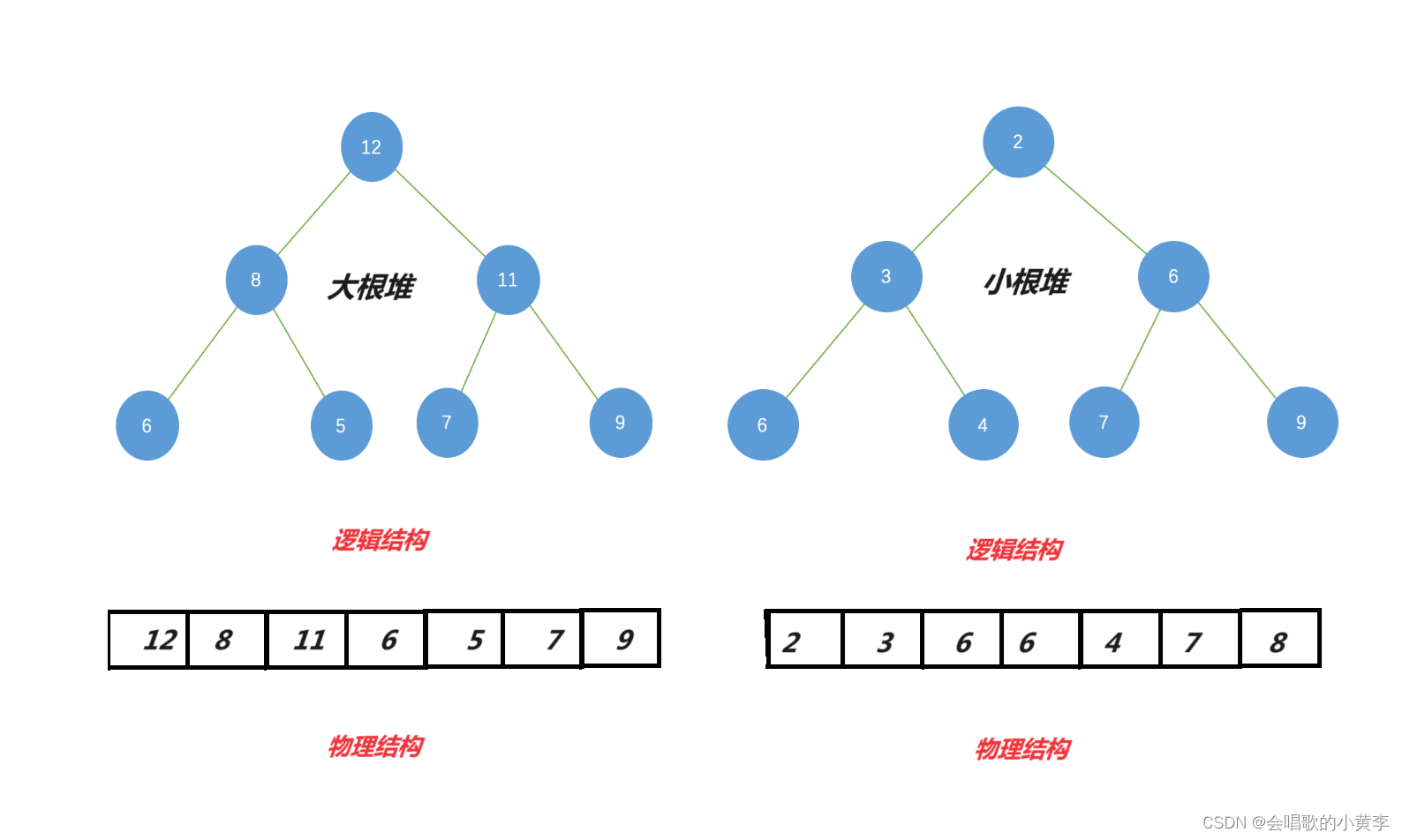
【大根堆和小根堆】:
根结点最大的堆叫做大根堆,树中所有父亲都大于或等于孩子。
根结点最小的堆叫做小根堆,树中所有父亲都小于或等于孩子。
堆的实现
首先新建一个工程:
Heap.h(堆的类型定义、接口函数声明、引用的头文件)
Heap.c(堆接口函数的实现)
test.c(主函数、测试栈各个接口功能)
完整的代码放在后面(包括测试代码),这里就不会展示测试的效果图。大家可以自己别敲边按测试代码测试。图解会写的很详细的,么么😙
堆的向下调整算法(建小堆为例)
现在我们给出一个数组,逻辑上看做一颗完全二叉树。我们通过从根节点开始的向下调整算法可以把它调整成一个小堆。
向下调整算法有一个前提:左右子树必须是一个堆,才能调整。
int arr[] = {27,15,19,18,28,34,65,49,25,37};
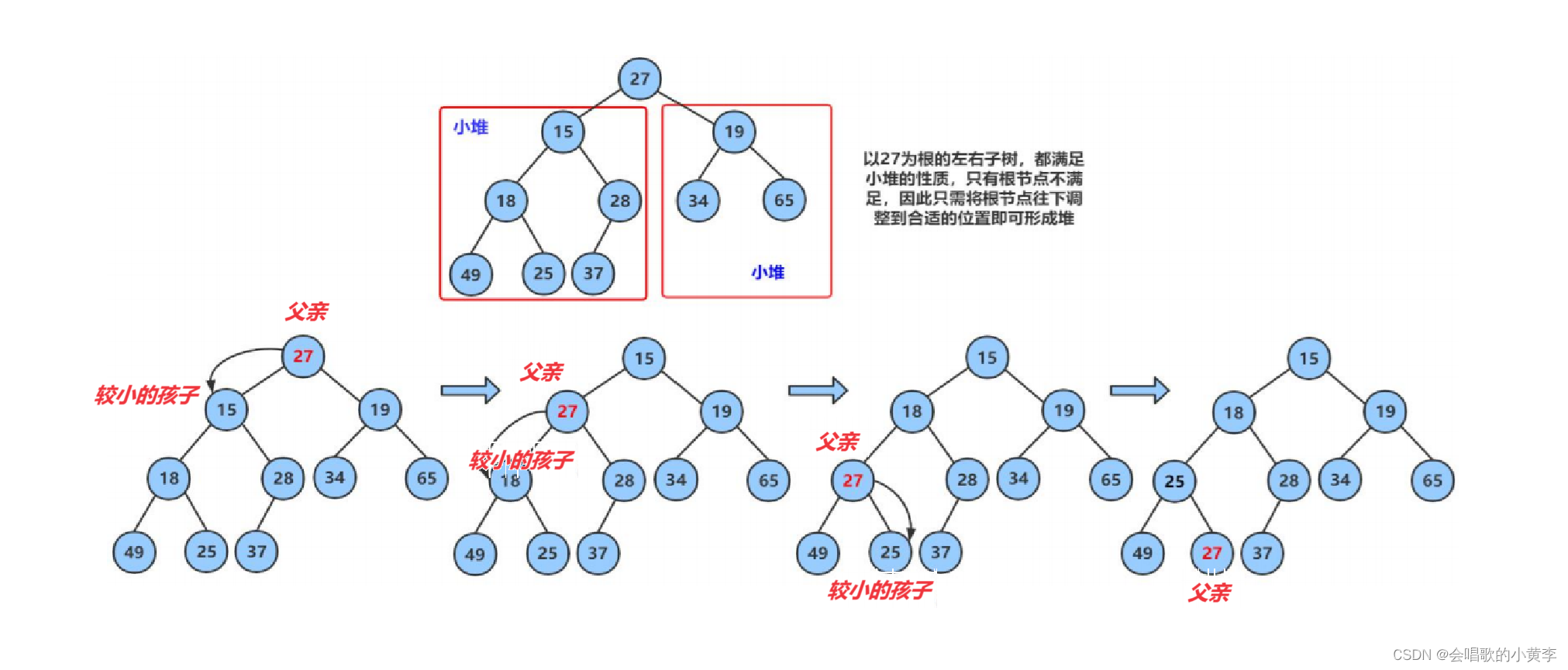
思想:
1.选出左右孩子较小的一个值,
2.然后和父亲进行比较,如果比父亲小就进行交换,并将原来小的孩子的位置当成父亲继续向下进行调整,直到调整到叶子结点为止。如果比父亲大,则停止向下调整,此时该树就成小堆。
//交换函数
void Swap(HDataType* p1, HDataType* p2)
{HDataType tmp = *p1;*p1 = *p2;*p2 = tmp;}//向下调整算法
void AdjustDown(HDataType* a, int size, int parent)
{//假设左孩子小int child = parent * 2 + 1;while (child < size){if (child + 1 < size && a[child + 1] < a[child])//确保有右孩子,如果右孩子小,更新到右边{++child;}if (a[child] < a[parent]){Swap(&a[child], &a[parent]);//更新父亲孩子下标,parent = child;child = child * 2 + 1;}else // 如果父亲小于孩子,说明已经为小堆了,停止调整{break;}}}
堆的向上调整算法(建小堆为例)
当我们在一个堆的末尾插入一个数据后,需要对堆进行调整,使其仍然是一个堆,这时需要用到堆的向上调整算法。
假设在这个堆int arr[] = {15,18,19,25,28,34,65,49,27,37}的末尾插入16.
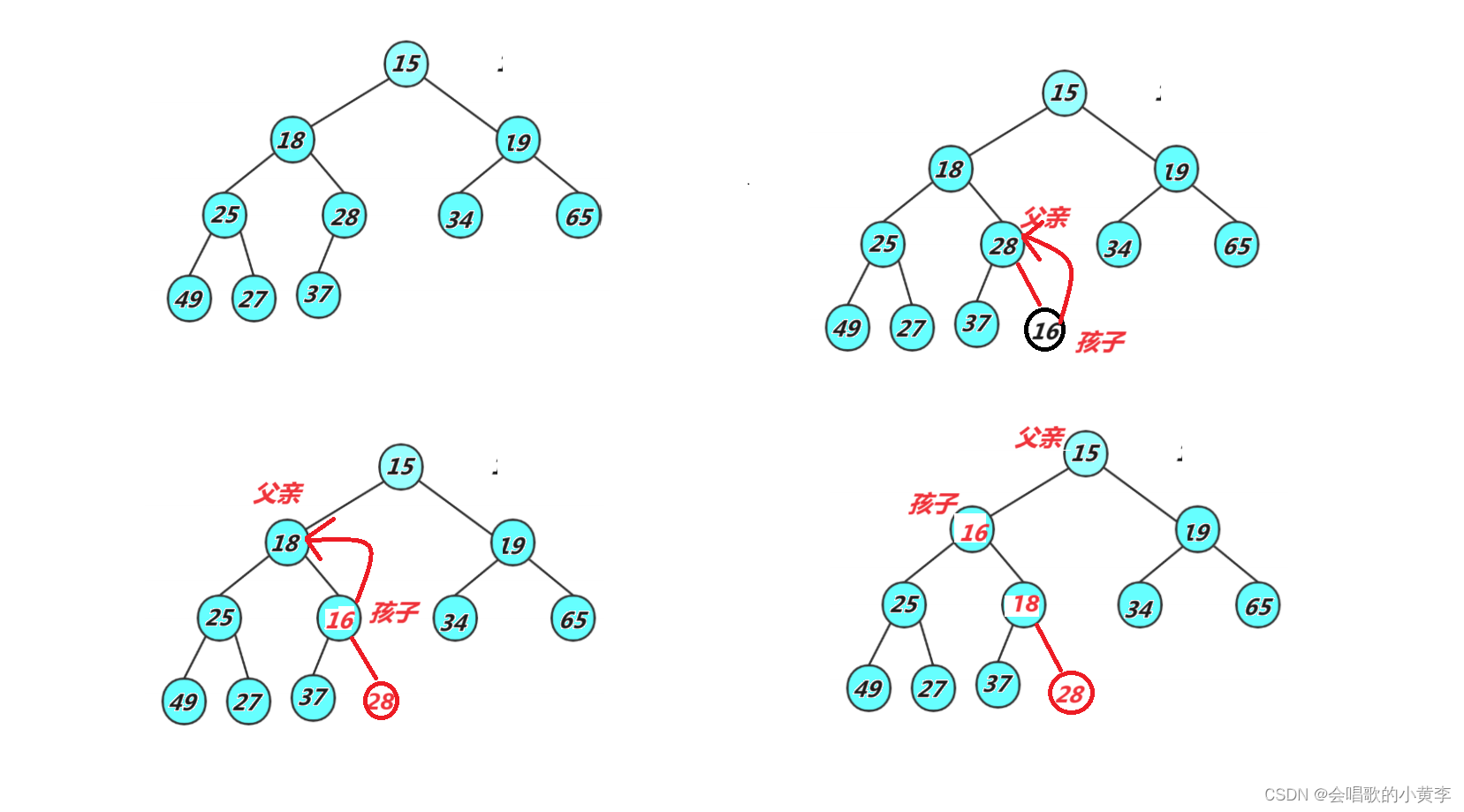
思想:
1.将要插入孩子的值与父亲的值比较。
2.若插入孩子的值比父亲的值小,则交换插入孩子的值与父亲的值,并将父亲的位置当作新的插入孩子的值继续进行向上调整。若插入孩子的值比父亲的值大,则停止向上调整,此时该树就成小堆。
//交换函数
void Swap(HDataType* p1, HDataType* p2)
{HDataType tmp = *p1;*p1 = *p2;*p2 = tmp;}//向上调整算法
void AdjustUp(HDataType* a, int child)
{int parent = (child - 1) / 2;while (child > 0){if (a[child] < a[parent]){Swap(&a[parent], &a[child]);child = parent;parent = (parent - 1) / 2;}else{break;}}
}
堆的初始化
//初始化堆
void HPInit(HP* php)
{assert(php);php->a = NULL;php->size = 0;php->capacity = 0;
}
销毁堆
//销毁堆
void HPDestroy(HP* php)
{assert(php);free(php->a);php->a = NULL;php->size = 0;php->capacity = 0;
}
堆的插入
数据插入时是插入到数组的末尾,即树形结构的最后一层的最后一个结点,所以插入数据后我们需要运用堆的向上调整算法对堆进行调整,使其在插入数据后仍然保持堆的结构。
//堆的插入
void HPPush(HP* php, HDataType x)
{assert(php);//检查空间是否足够插入,不够则扩容if (php->size == php->capacity){int newcapacity = php->capacity == 0 ? 4 : php->capacity * 2;HDataType* tmp = (HDataType*)realloc(php->a, sizeof(HDataType) * newcapacity);if (tmp == NULL){perror("realloc fail");exit(-1);}php->a = tmp;php->capacity = newcapacity;}//插入元素php->a[php->size] = x;php->size++;AdjustUp(php->a, php->size - 1);// 从插入的元素开始,进行向上调整,保持它依然是堆
}
堆的删除(规定删堆顶的数据)
堆的删除,删除的是堆顶的元素,但是这个删除过程可并不是直接删除堆顶的数据,
1.将堆顶的数据与最后一个结点的数据交换,
2.删除堆种最后一个元素,此时左子树和右子树还是小堆
3.再对堆进行向下调整
//堆的删除(规定删堆顶的数据)
void HPPop(HP* php)
{assert(php);assert(php->size > 0);//确保堆不能为空Swap(&php->a[0], &php->a[php->size - 1]);// 将堆顶元素和最后一个元素交换php->size--;// 删除堆中最后一个元素AdjustDown(php->a, php->size, 0);// 从根节点开始,对剩下元素进行向下调整成大堆,保持它依然是堆
}
取堆顶元素
//取堆顶元素
HDataType HPTop(HP* php)
{assert(php);assert(php->size > 0);//确保堆里有数据return php->a[0];//返回堆顶数据
}
判断堆是否为空
//判断堆是否为空
bool HPEmpty(HP* php)
{assert(php);return php->size == 0;//判断堆中数据是否为0
}
获取堆的个数
//获取堆的个数
int HPSize(HP* php)
{assert(php);return php->size;//返回堆中数据个数
}
完整代码(包括测试代码)
Heap.h
#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>typedef int HDataType;
typedef struct Heap
{HDataType* a;int size;int capacity;}HP;//交换函数
void Swap(HDataType* p1, HDataType* p2);
//向上调整算法
void AdjustUp(HDataType* a, int child);
//向下调整算法
void AdjustDown(HDataType* a, int size, int parent);//初始化堆
void HPInit(HP* php);
//销毁堆
void PHDestroy(HP* php);
//堆的插入
void HPPush(HP* php, HDataType x);
//堆的删除(规定删堆顶的数据)
void HPPop(HP* php);
//取堆顶元素
HDataType HPTop(HP* php);
//判断堆是否为空
bool HPEmpty(HP* php);
//获取堆的个数
int HPSize(HP* php);Heap.c
#define _CRT_SECURE_NO_WARNINGS 1
#include"Heap.h"//小堆
void Swap(HDataType* p1, HDataType* p2)
{HDataType tmp = *p1;*p1 = *p2;*p2 = tmp;}//向下调整算法
void AdjustDown(HDataType* a, int size, int parent)
{//假设左孩子小int child = parent * 2 + 1;while (child < size){ if (child + 1 < size && a[child + 1] < a[child])//确保有右孩子,如果错了,更新到右边{++child;}if (a[child] < a[parent]){Swap(&a[child], &a[parent]);parent = child;child = child * 2 + 1;}else{break;}}}
//向上调整算法
void AdjustUp(HDataType* a, int child)//可以用递归写,没必要,用循环就可以
{int parent = (child - 1) / 2;while (child > 0){if (a[child] < a[parent]){Swap(&a[parent], &a[child]);child = parent;parent = (parent - 1) / 2;}else{break;}}}
//初始化堆
void HPInit(HP* php)
{assert(php);php->a = NULL;php->size = 0;php->capacity = 0;
}//销毁堆
void HPDestroy(HP* php)
{assert(php);free(php->a);php->a = NULL;php->size = 0;php->capacity = 0;}//堆的插入
void HPPush(HP* php, HDataType x)
{assert(php);if (php->size == php->capacity){int newcapacity = php->capacity == 0 ? 4 : php->capacity * 2;HDataType* tmp = (HDataType*)realloc(php->a, sizeof(HDataType) * newcapacity);if (tmp == NULL){perror("realloc fail");exit(-1);}php->a = tmp;php->capacity = newcapacity;}php->a[php->size] = x;php->size++;AdjustUp(php->a, php->size - 1);
}//堆的删除(规定删堆顶的数据)
void HPPop(HP* php)
{assert(php);assert(php->size > 0);Swap(&php->a[0], &php->a[php->size - 1]);php->size--;AdjustDown(php->a, php->size, 0);
}//取堆顶元素
HDataType HPTop(HP* php)
{assert(php);assert(php->size > 0);return php->a[0];
}//判断堆是否为空
bool HPEmpty(HP* php)
{assert(php);return php->size == 0;
}
//获取堆的个数
int HPSize(HP* php)
{assert(php);return php->size;
}
test.c
#define _CRT_SECURE_NO_WARNINGS 1
#include"Heap.h"int main()
{int a[] = { 4,3,7,9,1,5,8,2,8 };int sz = sizeof(a) / sizeof(a[0]);HP hp;HPInit(&hp);for (int i = 0; i < sz; i++){HPPush(&hp, a[i]);}//int k = 5;//while (k--)//{// printf("%d\n", HPTop(&hp));// HPPop(&hp);//}while (!HPEmpty(&hp)){printf("%d ", HPTop(&hp));HPPop(&hp);}printf("\n");return 0;
}
相关文章:

【数据结构】堆(超详细)
文章目录 前言堆的概念及结构堆的实现堆的向下调整算法(建小堆为例)堆的向上调整算法(建小堆为例)堆的初始化销毁堆堆的插入堆的删除(规定删堆顶的数据)取堆顶元素判断堆是否为空获取堆的个数 完整代码(包括测试代码&a…...

常用正则 JS 持续更新
应用版本号正则验证 正则判断版本号(如:1.2.3 或 1.2.3.4),不允许出现 0.x.x;01.x.x; x.0x.x; x.00.x; x.x.00; x.x.0x/ ^ ([ 1-9 ] \d | [ 1-9 ])( . ([ 1-9 ] \d | \d )) {2,3} $ /0-10 保留一位小数的数…...
YOLO v6 iou_loss dfl_loss一直为0
Question img record infomation path is:…/mydata/images.train_cache.json Train: Final numbers of valid images: 1248/ labels: 1248. 0.1s for dataset initialization. img record infomation path is:…/mydata/images.val_cache.json Convert to COCO format 100%|█…...
FreeRTOS【4】线程挂起和恢复
1.开发背景 基于上一篇指引,成功创建并启动线程后,线程已经开始运行了,但是有时我们需要线程暂停运行,例如某个线程是控制 LED 闪灯的,如果现在需要让 LED 停止工作,单纯的关闭 LED 是没用的,因…...

CPU占用率过高排查
CPU占用率高是设备本身的一种现象,直观表现为display cpu-usage命令查询结果中整机CPU占用率“CPU usage”偏高,如超过70%。在网络运行中CPU高常常会导致其他业务异常,如BGP震荡、VRRP频繁切换、甚至设备无法登录。 通常,整机CPU占…...
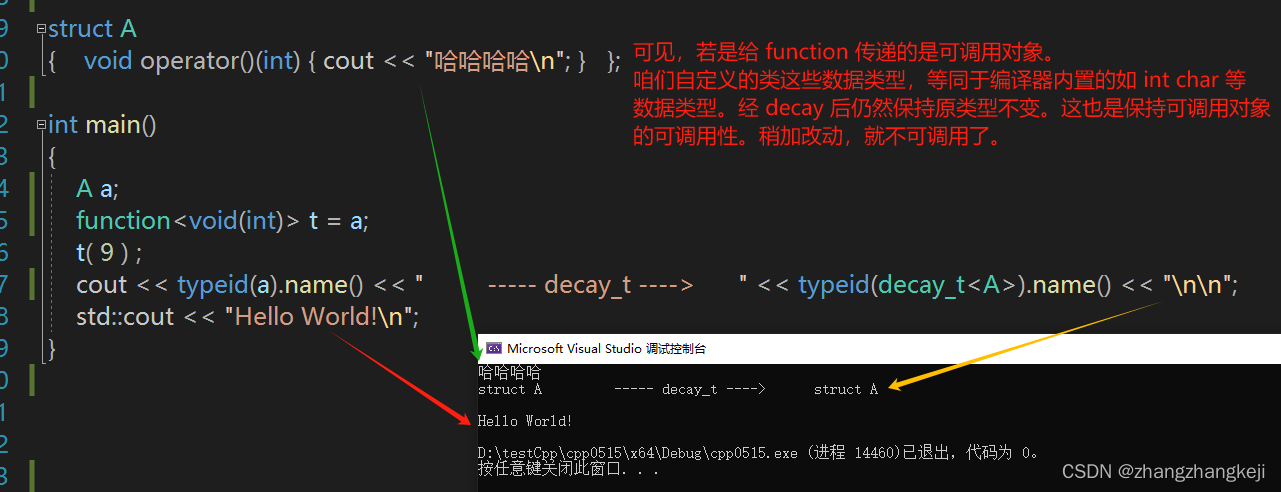
关于 vs2019 c++20 规范里的 STL 库里模板 decay_t<T>
(1) 这个模板,在库代码里非常常见。 decay 英文是“衰弱,消减” 的意思,大概能感觉到就是要简化模板参数 T 的类型,去掉其上的修饰符。因为常用且复杂,故单独列出其源码和注释。先举例其应用场景…...
android C++打印堆栈
Android在Java层打印堆栈比较方便,代码如下: try {throw new Exception("Debug xxx call stack"); }catch(Exception e) {e.printStackTrace(); }但是在C模块中能打印调用堆栈吗?怎么打印调用栈呢? 答案是肯定的&…...

MySQL Undo Log、Redo Log、bin Log
Undo Log 回滚日志,用于将数据回滚到之前的状态。 MySQL在进行数据的增、删、改时,会将数据写入到Undo Log日志中。 对于Undo Log存在着insert和update两种类型的数据。插入语句对应的是insert类型,修改、删除语句对应的是update类型。 U…...

vld.ini配置文件说明
vld.ini配置文件说明 ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;; ;; ;; Visual Leak Detector - 初始化/配置文件 ;; 版权所有 (c) 2005-2017 VLD团队 ;; ;; 本库是自由软件;你可以在自由软件基金会发布的GNU宽通用公共…...
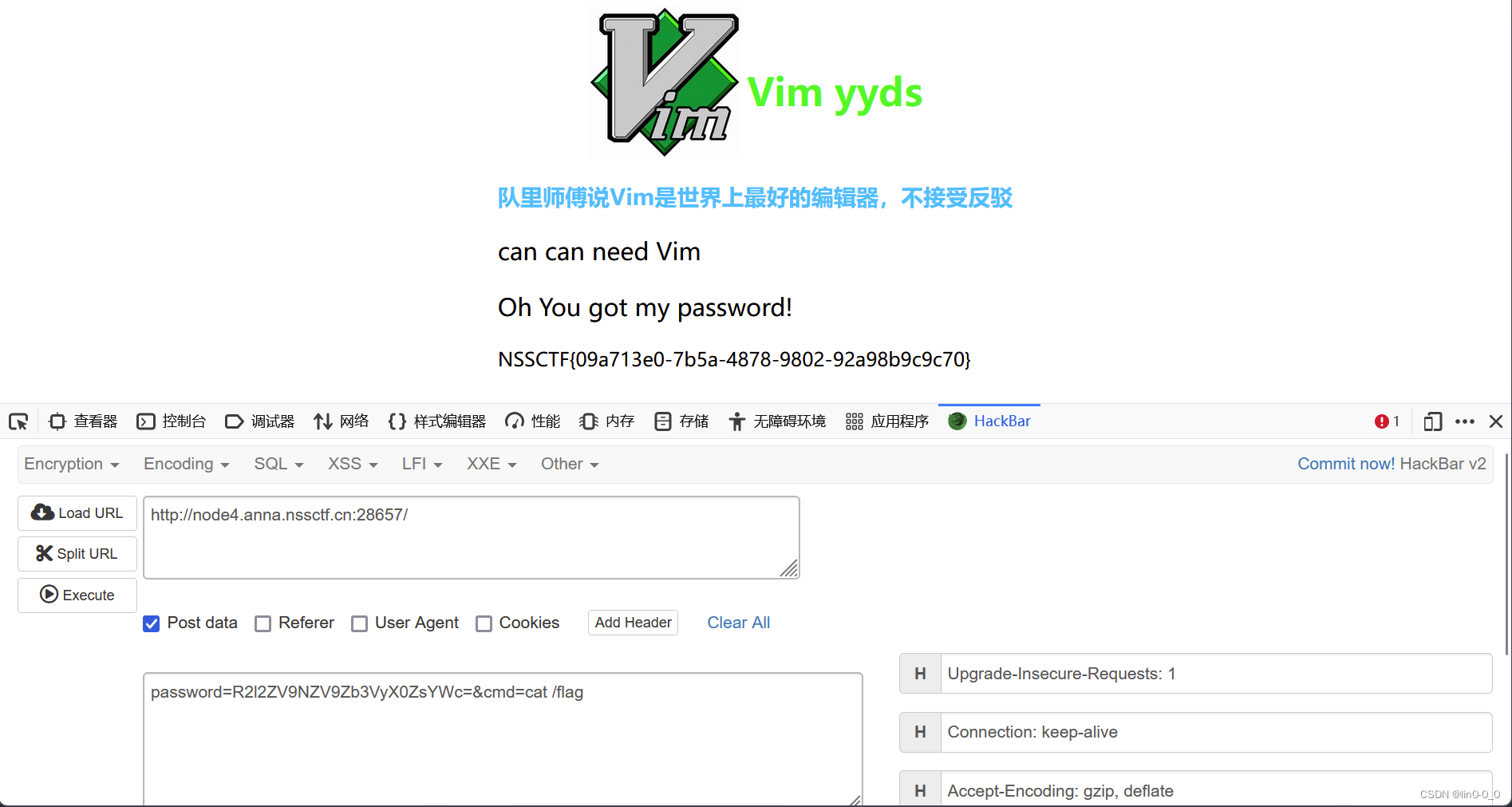
NSS【web】刷题
[SWPUCTF 2021 新生赛]jicao 类型:PHP、代码审计、RCE 主要知识点:json_decode()函数 json_decode():对JSON字符串解码,转换为php变量 用法: <?php $json {"ctf":"web","question"…...

将TailwindCSS默认单位rem转换为px
前言: 我这里需要将 默认的rem 转换为 px 原因是要使用 postcss-px-to-viewport 插件做移动端适配。 在tailwind.config.js文件中进行配置: 注意:这里 padding(内边距)、spacing(外边距)、width…...
)
命令模式(命令)
命令模式 文章目录 命令模式什么时命令模式通过示例了解命令模式 什么时命令模式 命令模式(Command),将一个请求封装为一个对象,从而使你可用不同的请求对客户进行参数化:对请求排队或记录请求日志,以及支持可撤销的操作。 通过示例了解命令模…...
Android ashmem 原理分析
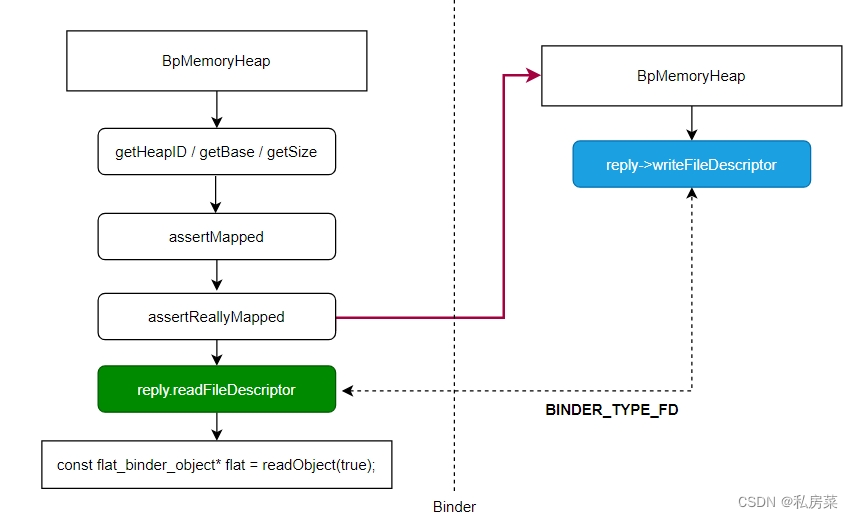
源码基于:Andoird U Kernel-5.10 0. 简介 ashmem 称为匿名共享内存(Anonymous Shared Memory),它以驱动程序的形式实现在内核空间中。它有两个特点: 能否辅助内存管理系统来有效地管理不再使用的内存块(pin / unpin); 通过Bind…...
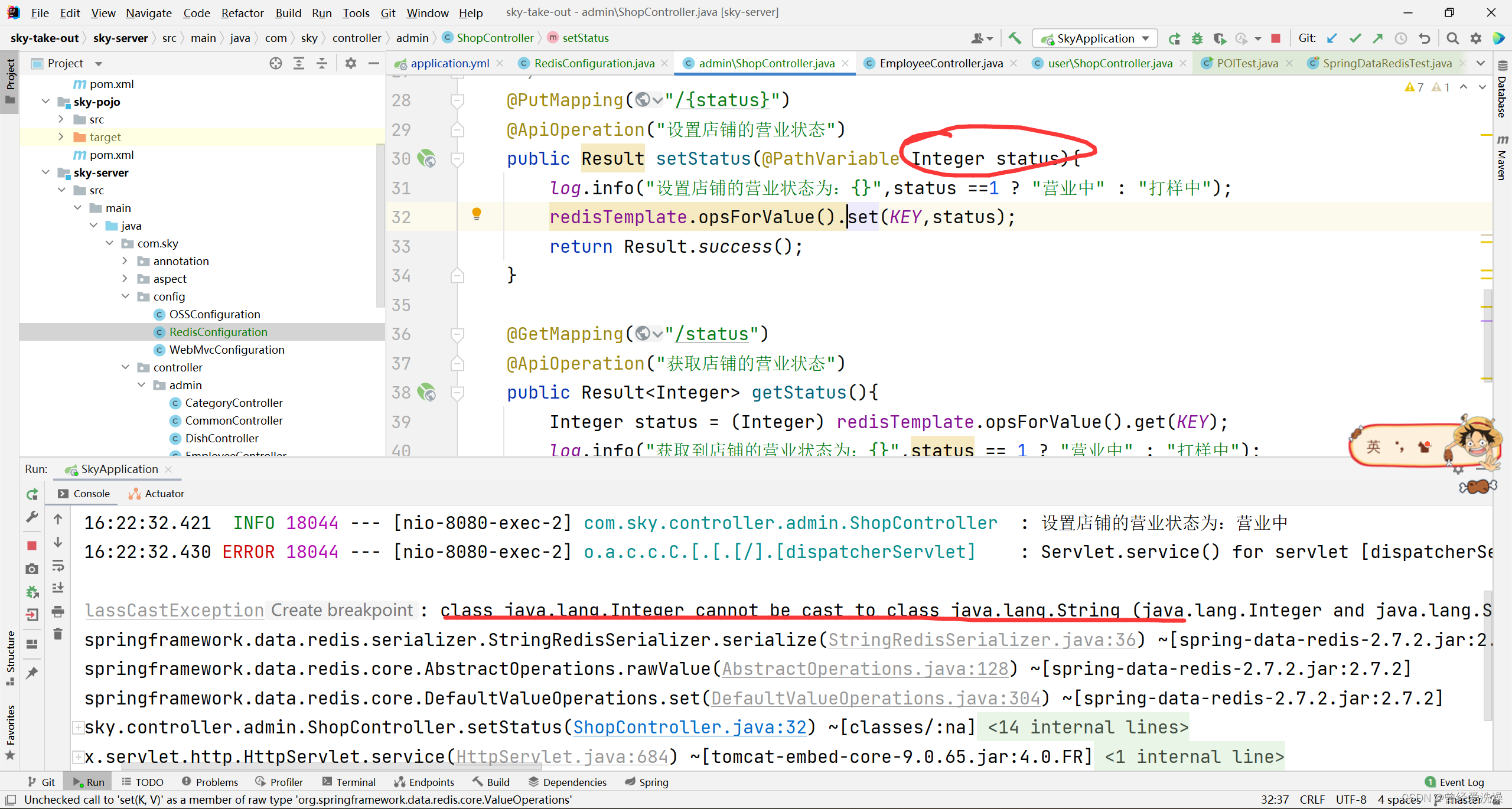
redis报错500
之前自己举一反三把value也给序列化了: 然后报错了: 原因是这里传入的是Integer类型,序列化的话就变为string类型了...

GPT-3
论文:Language Models are Few-Shot Learners(巨无霸OpenAI GPT3 2020) 摘要 最近的工作表明,通过对大量文本进行预训练,然后对特定任务进行微调,在许多NLP任务和基准方面取得了实质性进展。虽然这种方法…...

MATLAB数组
文章目录 数组创建通过冒号创建一维数组通过logspace函数创建一维数组通过linspace函数创建一维数组 通过randperm生成随机整数排列运算算术运算关系运算逻辑运算优先顺序 矩阵创建矩阵操作下标引用矩阵信息提取删除与扩展合并矩阵元素的运算矩阵运算 数组 在MATLAB中一般使用…...
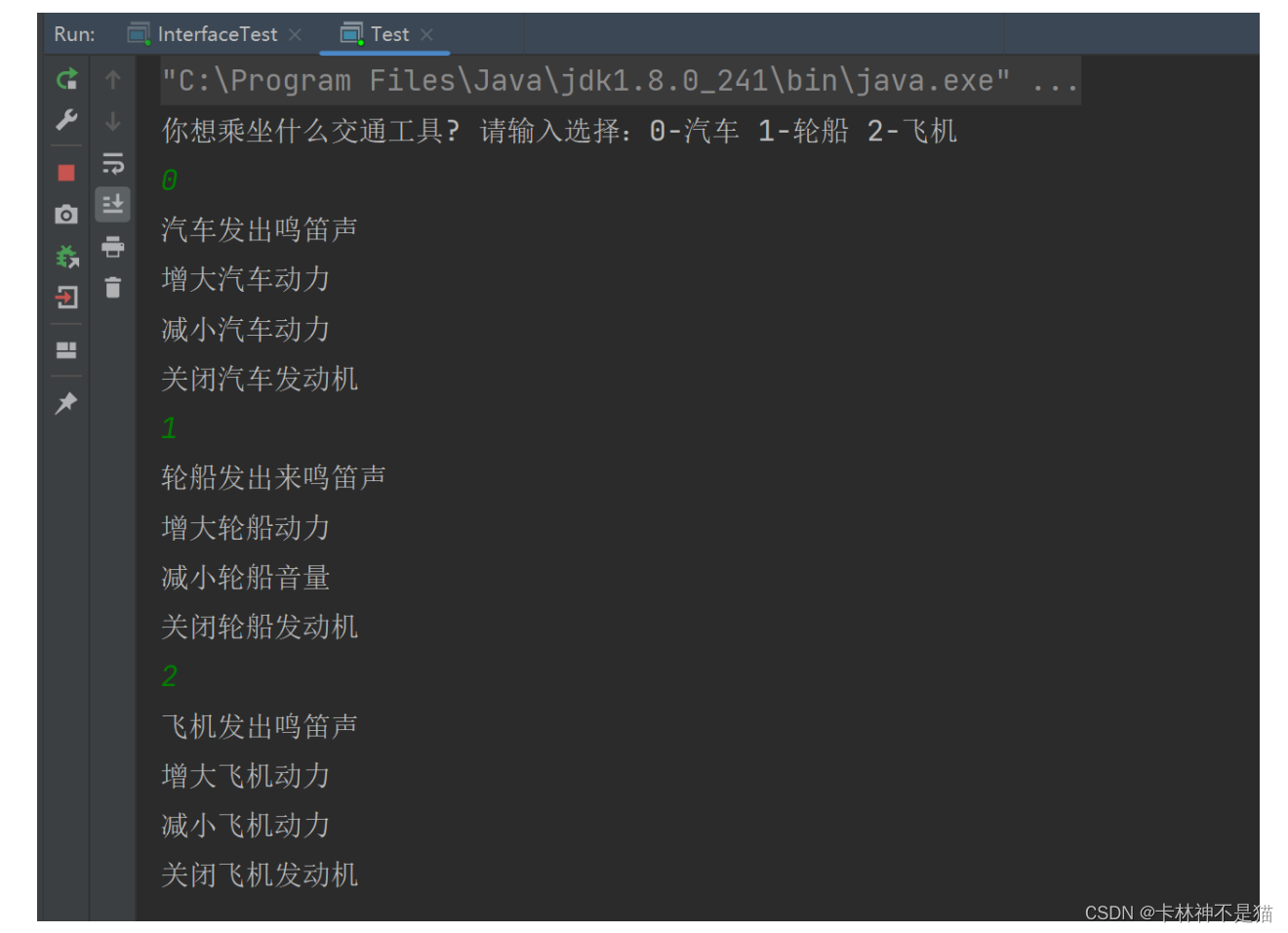
JAVA实验项目(二): 抽象类、接口的定义与使用
实验项目二 抽象类、接口的定义与使用 Tips:"分享是快乐的源泉💧,在我的博客里,不仅有知识的海洋🌊,还有满满的正能量加持💪,快来和我一起分享这份快乐吧😊&…...

JVM内存模型最新面试题(持续更新)
问题:java中创建的对象一般放在哪里?(全流程包含从创建到回收) 回答 大部分对象在堆中,这个基本都知道; 少部分对象是会在栈中的,比如作用域不局限于方法内的方法内部变量,这类对象的特征一般就是生命周期…...

Nginx wss to ws 折腾记
jssip 或 sipml5 <----wss--->nginx<---ws---->fs(5066) fs_cli -x sofia loglevel all 9 日志如下: REGISTER sip:192.168.43.135 SIP/2.0 Via: SIP/2.0/WSS df7jal23ls0d.invalid;branchz9hG4bKurFnCK9qJuXQlSrbszSL1S6wbCokKlLr;rport From: <…...

Java入门基础学习笔记22——程序流程控制
程序流程控制:控制程序的执行顺序。 程序有哪些执行顺序? 顺序、分支和循环。 分支结构: if、switch 循环: for、while、do-while 顺序结构是程序中最简单最基本的流程控制,没有特定的语法结构,按照代码…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...
中的KV缓存压缩与动态稀疏注意力机制设计)
大语言模型(LLM)中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型(LLM)参数规模的增长,推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长,而KV缓存的内存消耗可能高达数十GB(例如Llama2-7B处理100K token时需50GB内存&a…...
