【C++杂货铺铺】AVL树
目录
🌈前言🌈
📁 概念
📁 节点的定义
📁 插入
📁 旋转
1 . 新节点插入较高左子树的左侧---左左:右单旋
2. 新节点插入较高右子树的右侧---右右:左单旋
3. 新节点插入较高左子树的右侧---左右:先左单旋再右单旋
4. 新节点插入较高右子树的左侧---右左:先右单旋再左单旋
📁 性能
📁 完整代码
📁 总结
🌈前言🌈
欢迎观看本期【C++杂货铺】,这期内容讲解AVL树,包括了什么是AVL树,如何实现AVL树,此外还会分析二叉搜索树的性能。
学习本期内容之前,需要你对什么是二叉搜索树有一定的了解,如果不会很了解,或忘记可以快速阅览下面这篇文章:
【C++杂货铺】二叉搜索树-CSDN博客
📁 概念
在二叉搜索树中,规定比节点小的值都放在节点的左边,比几点大的值都放在节点的右边,可以大大缩短查找的效率。
但是如果数据有序或接近有序二叉搜索树将退化为单支树,查找元素相当于在顺序表中搜索元素,效率底下。
因此俄罗斯的两位数学家在1962年发明了一种解决上述问题的方法:当向二叉搜索树中插入新节点后,如果能保证每个节点的左右子树之差绝对值不超过1(需要对树中节点进行调整),即可降低树的高度,从而减少平均搜索长度。
一颗AVL树必须具有以下性质:
1. 它的左右子树都是AVL树.
2. 左右子树高度之差(简称平衡因子)的绝对值不超过1( -1 / 0 / 1).
如果一颗二叉搜索树是高度平衡的,那么它就是AVL树。如果它有n个节点,其高度可以维持在O(log N) ,搜索时间复杂度O(log N)。
📁 节点的定义
template<class T>
struct AVLTreeNode
{AVLTreeNode(const T& data): _pLeft(nullptr), _pRight(nullptr), _pParent(nullptr), _data(data), _bf(0){}AVLTreeNode<T>* _pLeft; // 该节点的左孩子AVLTreeNode<T>* _pRight; // 该节点的右孩子AVLTreeNode<T>* _pParent; // 该节点的双亲T _data;int _bf; // 该节点的平衡因子
};📁 插入
AVL树就是在二叉搜索树的基础上引入了平衡因子,因此AVL树也可以看成是二叉搜索树。
那么 AVL树的插入过程可以分为两步:
1. 按照二叉搜索树的方式插入新节点
2. 调整节点的平衡因子
bool Insert(const T& data)
{// 1. 先按照二叉搜索树的规则将节点插入到AVL树中// 2. 新节点插入后,AVL树的平衡性可能会遭到破坏,此时就需要更新平衡因子,并检测是否破坏了AVL树的平衡性/*pCur插入后,pParent的平衡因子一定需要调整,在插入之前,pParent的平衡因子分为三种情况:-1,0, 1, 分以下两种情况:1. 如果pCur插入到pParent的左侧,只需给pParent的平衡因子-1即可2. 如果pCur插入到pParent的右侧,只需给pParent的平衡因子+1即可此时:pParent的平衡因子可能有三种情况:0,正负1, 正负21. 如果pParent的平衡因子为0,说明插入之前pParent的平衡因子为正负1,插入后被调整成0,此时满足AVL树的性质,插入成功2. 如果pParent的平衡因子为正负1,说明插入前pParent的平衡因子一定为0,插入后被更新成正负1,此时以pParent为根的树的高度增加,需要继续向上更新3. 如果pParent的平衡因子为正负2,则pParent的平衡因子违反平衡树的性质,需要对其进行旋转处理*/while (pParent){// 更新双亲的平衡因子if (pCur == pParent->_pLeft)pParent->_bf--;elsepParent->_bf++;// 更新后检测双亲的平衡因子if (0 == pParent->_bf){break;}else if (1 == pParent->_bf || -1 == pParent->_bf){pCur = pParent;pParent = pCur->_pParent;}else{//根据不同情形,进行旋转...}}return true;
}
📁 旋转
1 . 新节点插入较高左子树的左侧---左左:右单旋
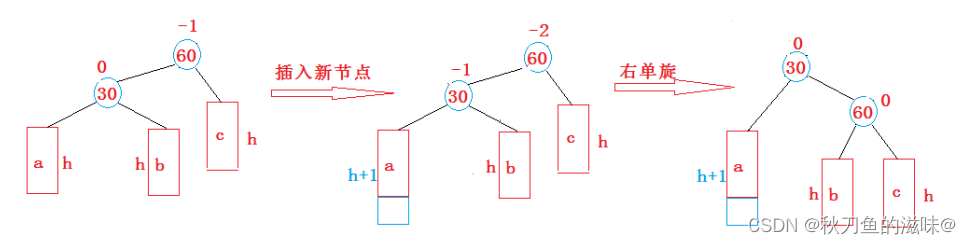
void RotateR(Node* parent)
{
Node* subL = parent->_left;
Node* subLR = subL->_right;parent->_left = subLR;
if (subLR)subLR->_parent = parent;subL->_right = parent;Node* pparent = parent->_parent;
parent->_parent = subL;
if (parent == _root)
{_root = subL;_root->_parent = nullptr;
}
else
{if (parent == pparent->_right){pparent->_right = subL;}else{pparent->_left = subL;}subL->_parent = pparent;}subL->_bf = parent->_bf = 0;
}2. 新节点插入较高右子树的右侧---右右:左单旋
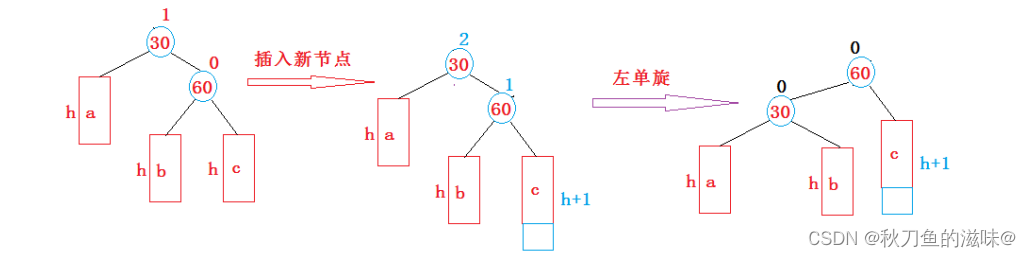
void RotateL(Node* parent)
{Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;if (subRL)subRL->_parent = parent;subR->_left = parent;Node* pparent = parent->_parent;parent->_parent = subR;if (parent == _root){_root = subR;_root->_parent = nullptr;}else{if (parent == pparent->_right){pparent->_right = subR;}else{pparent->_left = subR;}subR->_parent = pparent;}subR->_bf = parent->_bf = 0;
}3. 新节点插入较高左子树的右侧---左右:先左单旋再右单旋

void RotateLR(Node* parent)
{Node* subL = parent->_left;Node* subLR = subL->_right;int bf = subLR->_bf;RotateL(parent->_left);RotateR(parent);if (bf == 1){parent->_bf = 0;subL->_bf = -1;subLR->_bf = 0;}else if(bf == -1){parent->_bf = 1;subL->_bf = 0;subLR->_bf = 0;}else if (bf == 0){subLR->_bf = 0;subL->_bf = 0;parent->_bf = 0;}else{assert(false);}
}4. 新节点插入较高右子树的左侧---右左:先右单旋再左单旋
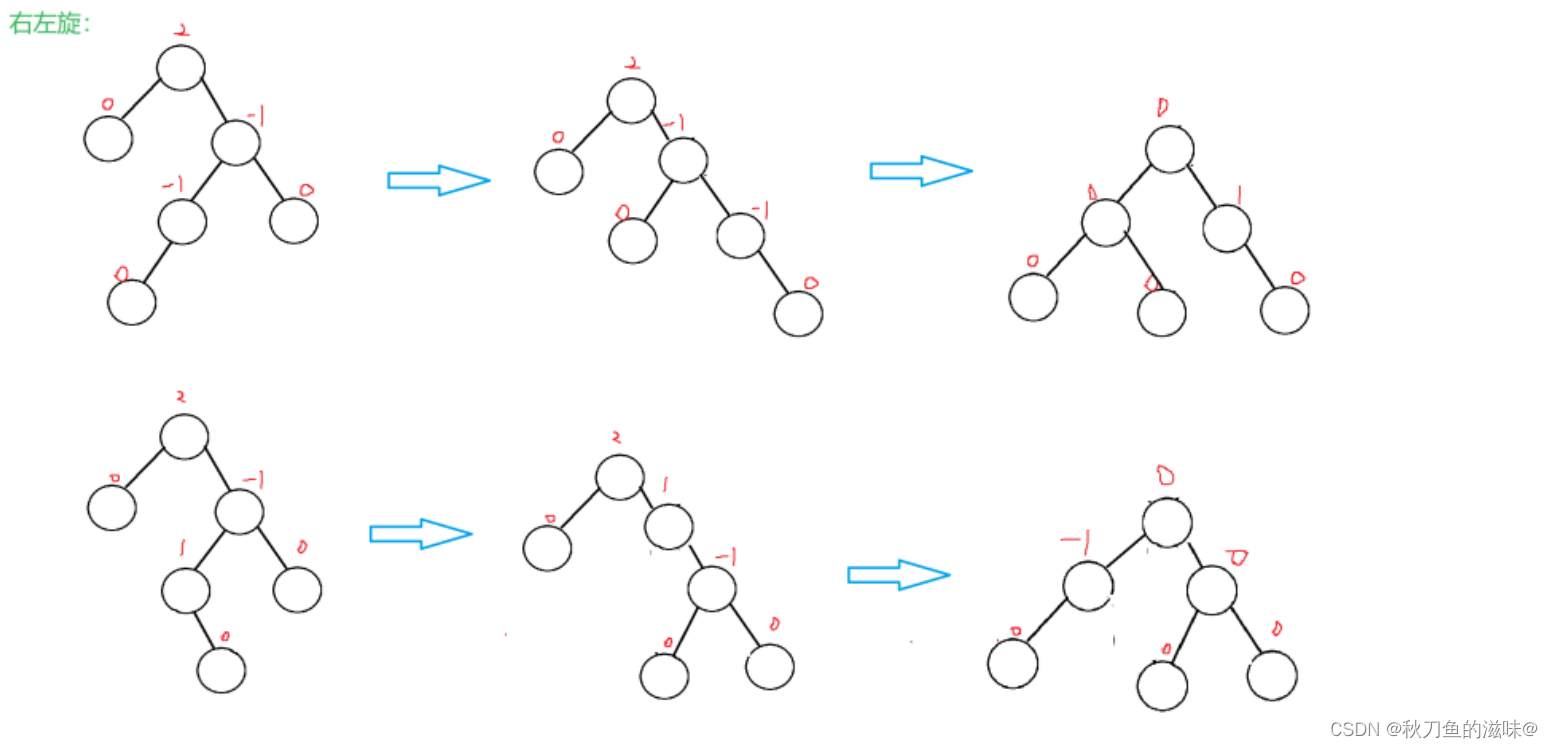
//右左单旋
void RotateRL(Node* parent)
{Node* subR = parent->_right;Node* subRL = subR->_left;int bf = subRL->_bf;RotateR(parent->_right);RotateL(parent);if (bf == 1){subRL->_bf = 0;parent->_bf = -1;subR->_bf = 0;}else if (bf == -1){subRL->_bf = 0;parent->_bf = 0;subR->_bf = 1;}else if(bf == 0){subRL->_bf = 0;parent->_bf = 0;subR->_bf = 0;}else{assert(false);}
}Node* _root = nullptr;
};AVL树是在二叉搜索树的基础上加入了平衡性的限制,因此要验证AVL树,可以分两步:
1. 验证其为二叉搜索树 如果中序遍历可得到一个有序的序列,就说明为二叉搜索树
2. 验证其为平衡树 每个节点子树高度差的绝对值不超过1(注意节点中如果没有平衡因子) 节点的平衡因子是否计算正确
📁 性能
AVL树是一棵绝对平衡的二叉搜索树,其要求每个节点的左右子树高度差的绝对值都不超过1,这 样可以保证查询时高效的时间复杂度,即log2 N。但是如果要对AVL树做一些结构修改的操 作,性能非常低下,比如:插入时要维护其绝对平衡,旋转的次数比较多,更差的是在删除时, 有可能一直要让旋转持续到根的位置。因此:如果需要一种查询高效且有序的数据结构,而且数 据的个数为静态的(即不会改变),可以考虑AVL树,但一个结构经常修改,就不太适合。
📁 完整代码
template<class T>
struct AVLTreeNode
{typedef AVLTreeNode<T> Node;AVLTreeNode(const T& val = T()):_left(nullptr), _right(nullptr), _parent(nullptr), _val(val), _bf(0){}Node* _left;Node* _right;Node* _parent;T _val;//平衡因子int _bf;
};template<class T>
class AVLTree
{typedef AVLTreeNode<T> Node;
public://插入bool Insert(const T& val){if (_root == nullptr){_root = new Node(val);return true;}Node* cur = _root;Node* parent = nullptr;while (cur){if (cur->_val> val){parent = cur;cur = cur->_left;}else if (cur->_val < val){parent = cur;cur = cur->_right;}else{return false;}}cur = new Node(val);if (parent->_val < val){parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent;//调整平衡因子while (parent){if (cur == parent->_right){parent->_bf++;}else{parent->_bf--;}if (parent->_bf == 0){break;}else if (parent->_bf == 1 || parent->_bf == -1){cur = parent;parent = parent->_parent;}else if (parent->_bf == 2 || parent->_bf == -2){//ROTATE//1. 右单旋if (parent->_bf == -2 && cur->_bf == -1){RotateR(parent);}//2. 左单旋else if (parent->_bf == 2 && cur->_bf == 1){RotateL(parent);}//3. 左右单旋else if (parent->_bf == -2 && cur->_bf == 1){RotateLR(parent);}//4. 右左单旋else if (parent->_bf == 2 && cur->_bf == -1){RotateRL(parent);}break;}else{assert(false);}}return true;}//遍历void Inorder(){_Inorder(_root);}//判断是否是平衡二叉树bool IsBalance(){return _IsBalance(_root);}int Height(){return _Height(_root);}protected:int _Height(Node* root){if (root == nullptr)return 0;return max(_Height(root->_right), _Height(root->_left)) + 1;}bool _IsBalance(Node* root){if (root == nullptr)return true;int leftsize = _Height(root->_left);int rightsize = _Height(root->_right);//检查右子树 - 左子树 < 2if (abs(rightsize - leftsize) >= 2){return false;}//检查平衡因子是否正确if (rightsize - leftsize != root->_bf)return false;return _IsBalance(root->_right)&& _IsBalance(root->_left);}void _Inorder(Node* root){if (root == nullptr){return;}_Inorder(root->_left);cout << root->_val << endl;_Inorder(root->_right);}//左单旋void RotateL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;if (subRL)subRL->_parent = parent;subR->_left = parent;Node* pparent = parent->_parent;parent->_parent = subR;if (parent == _root){_root = subR;_root->_parent = nullptr;}else{if (parent == pparent->_right){pparent->_right = subR;}else{pparent->_left = subR;}subR->_parent = pparent;}subR->_bf = parent->_bf = 0;}//右单旋void RotateR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR)subLR->_parent = parent;subL->_right = parent;Node* pparent = parent->_parent;parent->_parent = subL;if (parent == _root){_root = subL;_root->_parent = nullptr;}else{if (parent == pparent->_right){pparent->_right = subL;}else{pparent->_left = subL;}subL->_parent = pparent;}subL->_bf = parent->_bf = 0;}//左右单旋void RotateLR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;int bf = subLR->_bf;RotateL(parent->_left);RotateR(parent);if (bf == 1){parent->_bf = 0;subL->_bf = -1;subLR->_bf = 0;}else if(bf == -1){parent->_bf = 1;subL->_bf = 0;subLR->_bf = 0;}else if (bf == 0){subLR->_bf = 0;subL->_bf = 0;parent->_bf = 0;}else{assert(false);}}//右左单旋void RotateRL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;int bf = subRL->_bf;RotateR(parent->_right);RotateL(parent);if (bf == 1){subRL->_bf = 0;parent->_bf = -1;subR->_bf = 0;}else if (bf == -1){subRL->_bf = 0;parent->_bf = 0;subR->_bf = 1;}else if(bf == 0){subRL->_bf = 0;parent->_bf = 0;subR->_bf = 0;}else{assert(false);}}Node* _root = nullptr;
};📁 总结
以上就是本期【C++杂货铺】的主要内容了,主要验证了什么是AVL树,即一颗绝对平衡的二叉搜索树,通过平衡因子进行旋转平衡。展示了AVL树的模拟实现代码,深入理解了AVL树。
最后,如果感觉本期内容对你有帮助,欢迎点赞,收藏,关注。Thanks♪(・ω・)ノ

相关文章:

【C++杂货铺铺】AVL树
目录 🌈前言🌈 📁 概念 📁 节点的定义 📁 插入 📁 旋转 1 . 新节点插入较高左子树的左侧---左左:右单旋 2. 新节点插入较高右子树的右侧---右右:左单旋 3. 新节点插入较高左…...
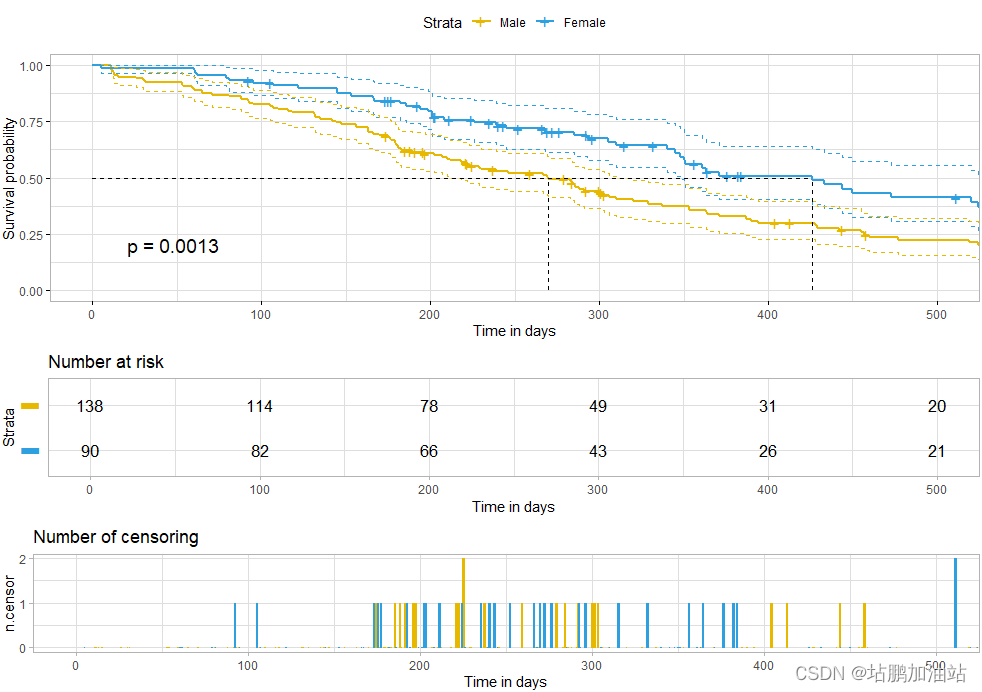
【R语言】生存分析模型
生存分析模型是用于研究时间至某个事件发生的概率的统计模型。这个事件可以是死亡、疾病复发、治疗失败等。生存分析模型旨在解决在研究时间相关数据时的挑战,例如右侧截尾(右侧截尾表示未观察到的事件发生,例如研究结束时还未发生事件&#…...

「AIGC」Python实现tokens算法
本文主要介绍通过python实现tokens统计,避免重复调用openai等官方api,开源节流。 一、设计思路 初始化tokenizer使用tokenizer将文本转换为tokens计算token的数量二、业务场景 2.1 首次加载依赖 2.2 执行业务逻辑 三、核心代码 from transformers import AutoTokenizer imp…...

【Unity】编程感悟20240510
【背景】 这一点感悟是过去有所认识,但是最近写Unity项目,涉及UDP通信需要持续监听逻辑时更加感受深刻的。 选用合适的触发点,用明确的逻辑避免循环处理 尽量采用明确的触发点使逻辑清晰,规避一定时间刷新这类的逻辑。 比如UDP…...

C#【进阶】泛型
1、泛型 文章目录 1、泛型1、泛型是什么2、泛型分类3、泛型类和接口4、泛型方法5、泛型的作用思考 泛型方法判断类型 2、泛型约束1、什么是泛型2、各泛型约束3、约束的组合使用4、多个泛型有约束思考1 泛型实现单例模式思考2 ArrayList泛型实现增删查改 1、泛型是什么 泛型实现…...
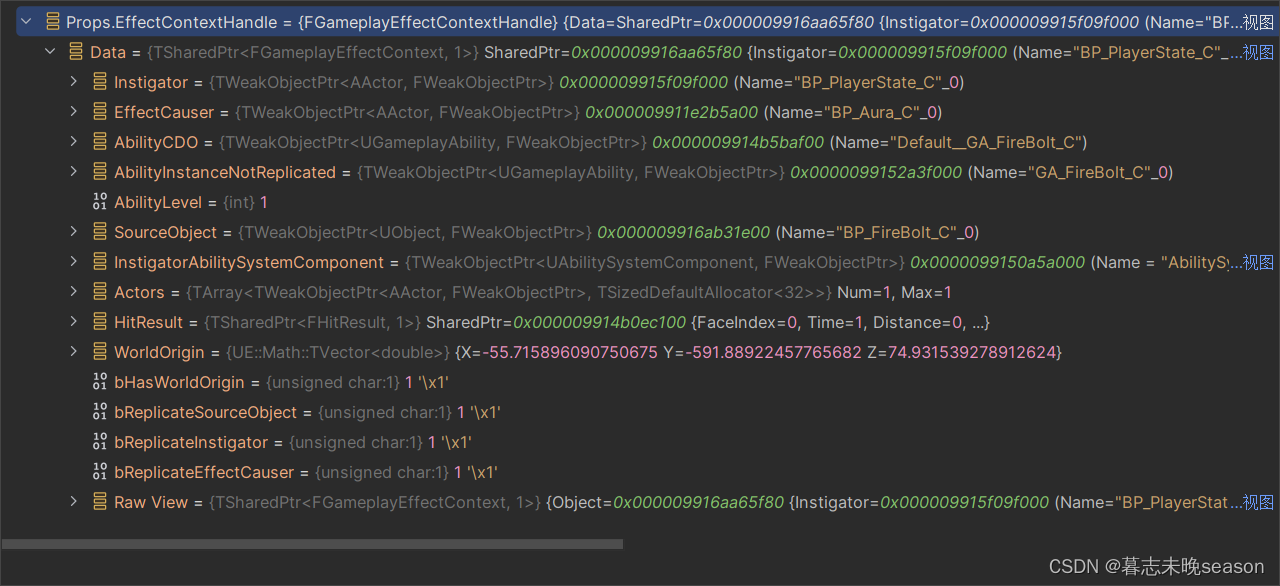
50. UE5 RPG FGameplayEffectContext
接下来,我想实现处理完伤害时,将伤害的触发格挡或者触发暴击时的逻辑传递到数据集的PostGameplayEffectExecute里面,这样,在处理IncomingDamage时,我们可以通过释放触发格挡或者触发暴击在UI上面进行对应的效果表现。 …...

Golang 的 unmarshal 踩坑指南
文章目录 1. 写在最前面2. 字段区分出空字段还是未设置字段2.1 问题描述2.2 解决 3. 字段支持多种类型 & 按需做不同类型处理3.1 问题描述3.2 解决 4. 碎碎念5. 参考资料 1. 写在最前面 笔者最近在实现将内部通知系统的数据定义转化为产品定义的对外提供的数据结构。 举例…...
Linux的常用指令 和 基础知识穿插巩固(巩固知识必看)
目录 前言 ls ls 扩展知识 ls -l ls -a ls -al cd cd 目录名 cd .. cd ~ cd - pwd 扩展知识 路径 / cp [选项] “源文件名” “目标文件名” mv [选项] “源文件名” “目标文件名” rm 作用 用法 ./"可执行程序名" mkdir rmdir touch m…...

MP3解码入门(基于libhelix)
主要参考资料: 【Arduino Linux】基于 Helix 解码库实现 MP3 音频播放: https://blog.csdn.net/weixin_42258222/article/details/122640413 libhelix-mp3: https://github.com/ultraembedded/libhelix-mp3/tree/master 目录 一、MP3文件二、MP3 解码库三、libhelix-mp3库3.1 …...
)
Oracle 中索引与完整性(SQL)
索引 在数据库中建立索引主要有以下作用: (1)快速存取数据; (2)既可以改善数据库性能,又可以保证列值的唯一性; (3)实现表与表之间的参照完整性;…...
】)
【Linux深度学习笔记5.13(Apache)】
Apache : 1.安装yum -y install hhtpd2.启动hhtpd -k start3.停止httpd -k stop4.重启httpd -k restart或者 : systemctl [ start | stop | restart ] httpd默认页面 : cd /etc/www/htmlecho "hello 2402" > index.html验证 : 浏览器访问 : http://ip 访问控制…...

汇编语言入门:探索 x86 架构
目录 前言 1. x86 语言 x86 架构简介 x86 架构的特点 x86 架构的演变 x86 架构的应用 2. 常用汇编指令集 3. 寻址方式 结语 前言 汇编语言是一种低级编程语言,直接面向计算机的硬件架构。在计算机科学中,了解汇编语言是非常重要的,因…...

[ffmpeg处理指令]
1 将h264转为mp4 ffmpeg -f h264 -i front_far_0.264 -vcodec copy front_far_0.mp4 ffmpeg -f h264 -i front_near_0.264 -vcodec copy front_near_0.mp4 -i:表示输入文件 front_far_2.mp4:表示输出文件 2 h264转为图片 front_far 是目标路径,需要…...
测试之路 - 精准而优雅
引子 这几年业内一直在做精准测试,大都使用工具 diff 代码改动、分析代码覆盖率这些平台集成的能力。 业务测试中,我们在技术设计和代码实现的基础上也做了一些精减和精准的测试实践,通过深入测试有针对的设计 case,发现隐藏问题…...

Java基础篇常见面试问题总结
文章目录 1. 你是怎样理解 OOP面向对象?2. 重载与重写区别3. 接口与抽象类的区别4. 深拷贝与浅拷贝的理解5. 什么是自动拆装箱? int和 Integer有什么区别6. 和 equals()区别7. String类 能被继承吗为什么用 final修饰8. final、finally、finalize区别 1. 你是怎样理…...

Spring、SpringMVC
一、Spring框架中的单例Bean是线程安全的吗? 【默认单例的情况下】Spring Bean并没有可变的状态(如Service类和DAO类),即只能查不能改,所以没有并发问题,所以某种程度上来说Spring的单例Bean是线程安全的。…...

【传知代码】VRT: 关于视频修复的模型(论文复现)
前言:随着数字媒体技术的普及,制作和传播视频内容变得日益普遍。但是,视频中由于多种因素,例如传输、存储和录制设备等,经常出现质量上的问题,如图像模糊、噪声干扰和低清晰度等。这类问题对用户的体验和观…...

不用投稿邮箱,怎样向各大新闻媒体投稿?
身为单位的信息宣传员,我深知肩上责任重大。每个月,完成单位在媒体上投稿发表文章的考核任务,就如同一场无声的赛跑,既要保证速度,更要注重质量。起初,我遵循“前辈们”的老路,一头扎进了邮箱投稿的海洋。但很快,现实给了我一记重拳——邮箱投稿的竞争犹如千军万马过独木桥,稿件…...
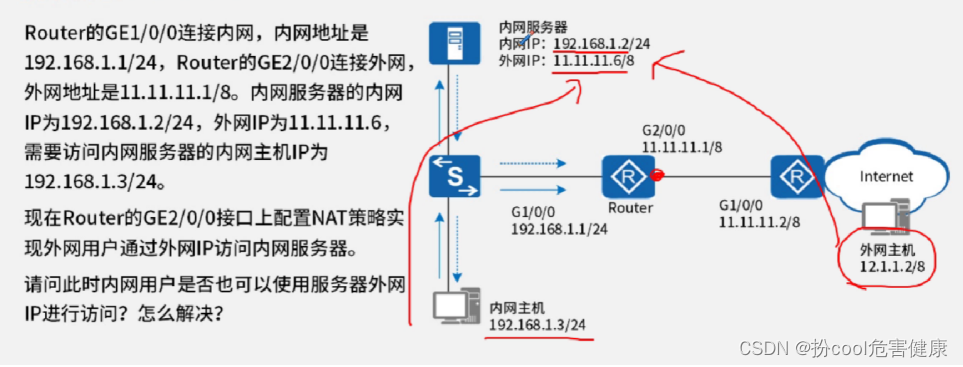
NAT技术总结与双向NAT配置案例
NAT的转换方式: 1.静态转换:固定的一对一IP地址映射。 interface GigabitEthernet0/0/1 ip address 122.1.2.24 nat static global 122.1.2.1 inside 192.168.1.1 #在路由器出接口 公网地址 私网地址。 2.动态转换:Basic NAT nat address-gr…...

mysql的explain
explain可以用于select,delete,insert,update的statement。 当explain用于statement时,mysql将会给出其优化器(optimizer)的执行计划。 通过explain字段生成执行计划表。下面来解析这个执行计划表的每一列…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...

Go 语言并发编程基础:无缓冲与有缓冲通道
在上一章节中,我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道,它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好࿰…...

