系列介绍:《创意代码:Processing艺术编程之旅》
系列介绍:《创意代码:Processing艺术编程之旅》
标题创意:
- “代码绘梦:Processing艺术编程入门”
- “数字画布:用Processing创造视觉奇迹”
- “编程美学:Processing艺术创作指南”
- “创意编程:Processing带你探索艺术新境界”
- “代码与色彩:Processing艺术编程实战”
- “艺术编程:Processing让你的创意无限延伸”
- “数字艺术家:Processing编程创作秘籍”
- “编程艺术:Processing开启你的创意之旅”
- “创意代码:Processing艺术编程进阶”
- “艺术与科技:Processing编程艺术探索”
内容规划:
- 入门篇:介绍Processing的基本概念、环境搭建和基础语法,让读者快速上手。
- 图形与动画:讲解如何使用Processing绘制图形、创建动画,并探索颜色和形状的无限可能。
- 交互设计:教授如何添加交互元素,如鼠标和键盘事件,使作品更具互动性。
- 数据可视化:展示如何将数据转化为视觉艺术,让复杂信息一目了然。
- 高级技巧:深入探讨Processing的高级功能,如3D绘图、物理模拟和声音处理。
- 项目实战:通过实际项目案例,指导读者如何将所学知识应用于创作中。
- 社区与资源:介绍Processing社区、在线资源和相关工具,帮助读者持续学习和创作。
相关文章:

系列介绍:《创意代码:Processing艺术编程之旅》
系列介绍:《创意代码:Processing艺术编程之旅》 标题创意: “代码绘梦:Processing艺术编程入门”“数字画布:用Processing创造视觉奇迹”“编程美学:Processing艺术创作指南”“创意编程:Proc…...
深度学习设计模式之抽象工厂模式
文章目录 前言一、介绍二、详细分析1.核心组成2.实现步骤3.代码示例4.优缺点优点缺点 5.使用场景 总结 前言 本文主要学习抽象工厂模式,抽象工厂模式创建的是对象家族,比如:苹果是一个产品,但是他不单单只生产手机,还…...

K8s是什么?
url address K8s是一个开源的容器编排平台,可以自动化,在部署,管理和扩展容器化应用过程中涉及的许多手动操作。 Kubernetes最初是由Google工程师作为Borg项目开发和设计的,后于2015年捐赠给云原生计算基金会(CNCF&a…...
【网站项目】SpringBoot796水产养殖系统
🙊作者简介:拥有多年开发工作经验,分享技术代码帮助学生学习,独立完成自己的项目或者毕业设计。 代码可以私聊博主获取。🌹赠送计算机毕业设计600个选题excel文件,帮助大学选题。赠送开题报告模板ÿ…...

Vue详细介绍
Vue.js(通常简称为Vue)是一个用于构建用户界面的渐进式JavaScript框架。它由尤雨溪(Evan You)创建,并于2014年首次发布。Vue的设计目的是易于上手,同时也能够强大到驱动复杂的单页应用(SPA&…...
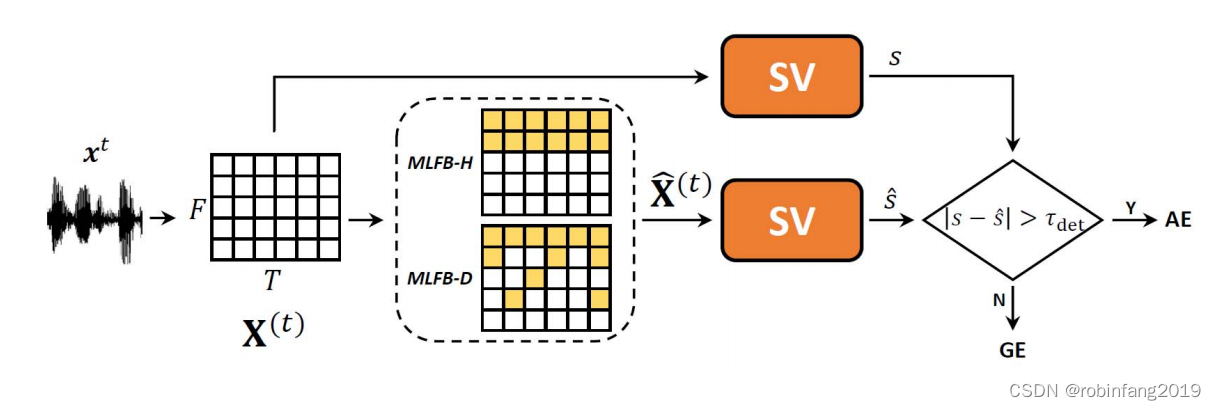
声纹识别的对抗与防御
随着机器学习理论和方法的发展, 出现了用于模仿特定说话人语音的深度伪造、针对语音识别和声纹识别的对抗样本, 它们都为破坏语音载体的可信性和安全性提供了具体手段, 进而对各自应用场景的信息安全构成了挑战。 深度伪造是利用生成式对抗网络等方法, 通过构建特定的模型, 产生…...

C++ QT设计模式总结
Ciallo~(∠・ω< )⌒★,这里是 Eureka,欢迎来看我的设计模式总结,有问题随时可以告诉我~ 面向对象的设计模式: 以下总结了面向对象的设计模式, QT 的源码在哪里体现了这些模式,以及如何在 …...
)
洛谷 P3203:弹飞绵羊 ← 分块算法(单点更新、单点查询)
【题目来源】https://www.acwing.com/problem/content/2168/https://www.luogu.com.cn/problem/P3203【题目描述】 某天,Lostmonkey 发明了一种超级弹力装置,为了在他的绵羊朋友面前显摆,他邀请小绵羊一起玩个游戏。 游戏一开始,L…...
程序验证之Dafny--证明霍尔逻辑的半自动化利器
一、What is Dafny?【来自官网介绍 Dafny 】 1)介绍 Dafny 是一种支持验证的编程语言,配备了一个静态程序验证器。 通过将复杂的自动推理与熟悉的编程习语和工具相结合,使开发者能够编写可证明正确的代码(相对于 {P}S{Q} 这种…...

Flutter 中的 SafeArea 小部件:全面指南
Flutter 中的 SafeArea 小部件:全面指南 在移动应用开发中,处理设备屏幕的边缘是一个常见的挑战,尤其是考虑到现代设备通常具有不同的屏幕形状,如刘海屏、曲面屏等。为了确保应用内容不会覆盖这些屏幕区域,Flutter 提…...
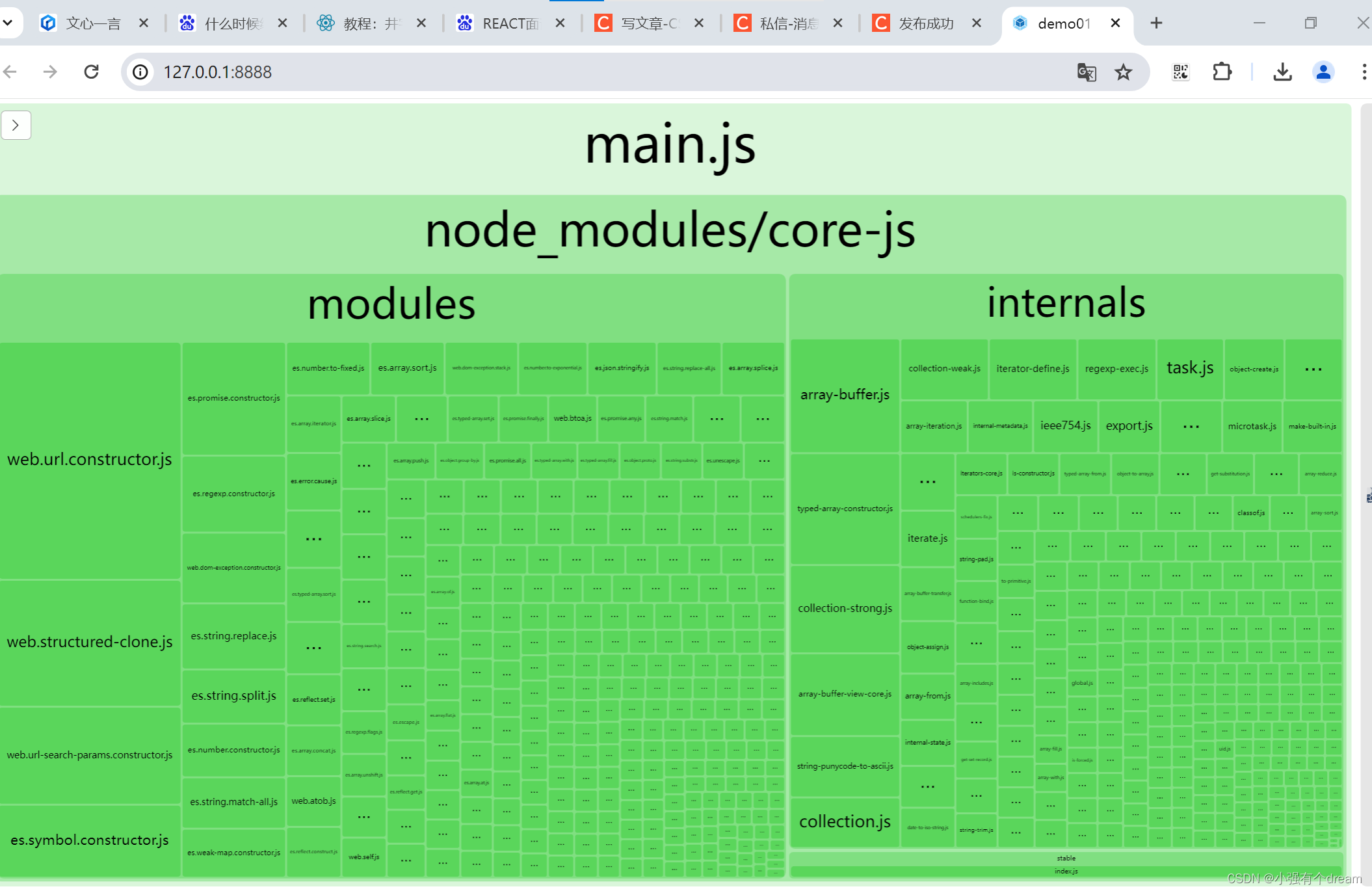
webpack生成模块关系依赖图示例:查看构建产物的组成部分 依赖关系图
npm i -D webpack-bundle-analyzer core-js babel-loaderwebpack.config.js const BundleAnalyzerPlugin require(webpack-bundle-analyzer).BundleAnalyzerPlugin; module.exports {entry: ./src/index.js,output: {filename: main.js,},// mode: production, // 或者 produ…...

Spacy的安装与使用教程
官网安装指导教程 https://spacy.io/usage 安装指令 需要根据自己系统的cuda版本选择 nvcc -V pip install -U pip setuptools wheel pip install -U spacy[cuda12x] python -m spacy download zh_core_web_sm python -m spacy download en_core_web_sm...

Pathlib,一个不怕迷路的 Python 向导
大家好!我是爱摸鱼的小鸿,关注我,收看每期的编程干货。 一个简单的库,也许能够开启我们的智慧之门, 一个普通的方法,也许能在危急时刻挽救我们于水深火热, 一个新颖的思维方式,也许能…...

详解绝对路径和相对路径的区别
绝对路径和相对路径是用于描述文件或目录在文件系统中位置的两种不同方式。 绝对路径(Absolute Path)是从文件系统的根目录开始的完整路径,可以唯一地确定一个文件或目录的位置。在不同的操作系统中,根目录的表示方式可能略有不同…...
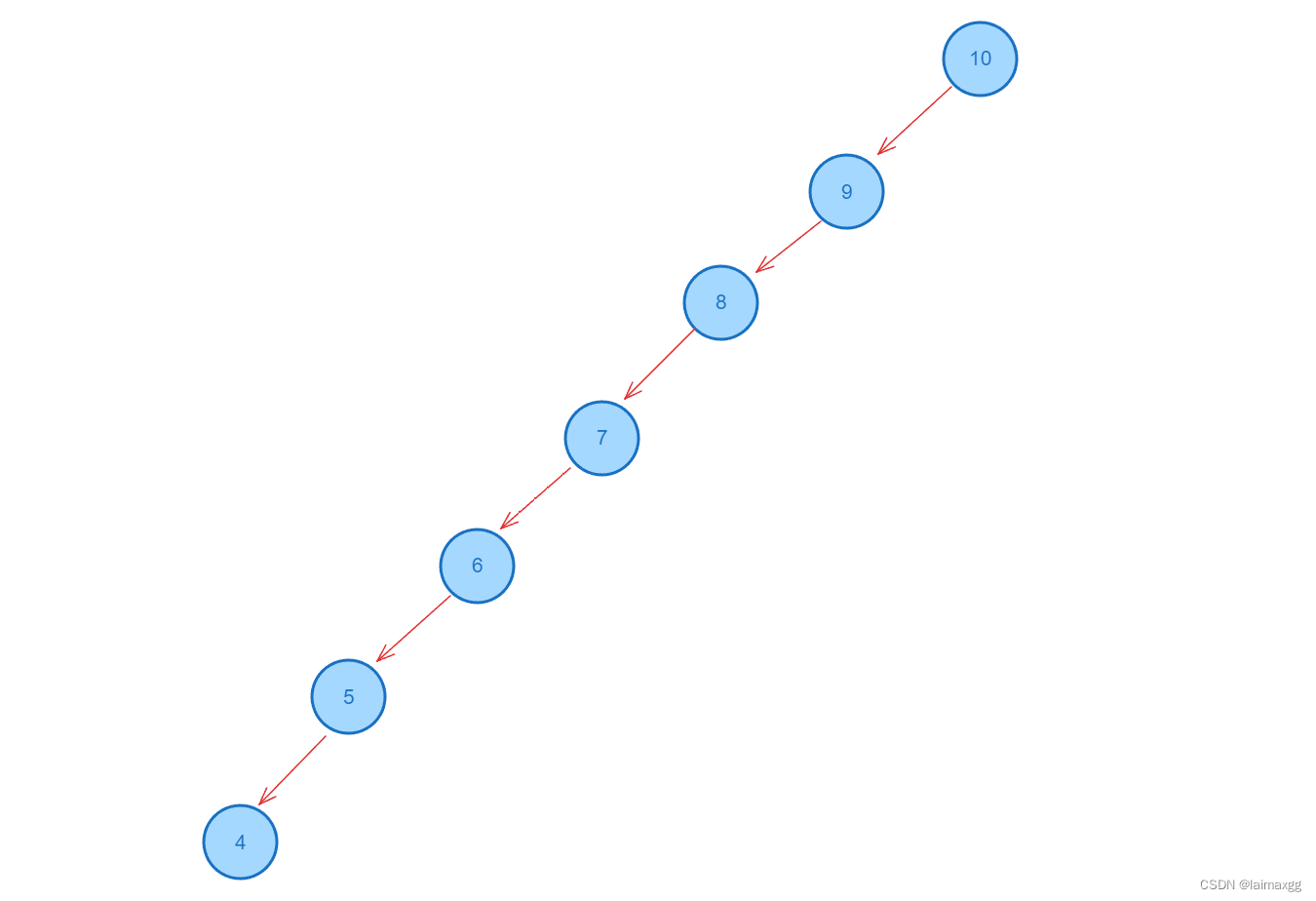
C++二叉搜索树搜索二叉树二叉排序树
C二叉搜索树 1. 二叉搜索树的概念 二叉搜索树(BST,Binary Search Tree),也称为二叉排序树或二叉查找树。它与一般二叉树的区别在于:每个结点必须满足“左孩子大于自己,右孩子小于自己”的规则。在这种规则的约束下,二…...

Java 自然排序和比较器排序区别?Comparable接口和Comparator比较器区别?
注:如果你对排序不理解,请您耐心看完,你一定会明白的。文章通俗易懂。建议用idea运行一下案例。 1)自然排序和比较器排序的区别? 自然排序是对象本身定义的排序规则,由对象实现 Comparable 接口ÿ…...

【CV】opencv调用DIS/LK等计算光流,前一帧和当前帧写反了有什么影响?
当在计算光流时,将前一帧和当前帧输入反了,会导致一系列问题。 在计算光流时,通常是将前一帧作为模板,根据当前帧计算光流。因为光流是描述相邻帧之间像素移动的一种方法,它通过比较两帧之间的像素强度或特征点的移动…...

C语言学习细节|C语言面向对象编程!函数指针如何正确使用
文章目录 1.函数指针定义2.格式3.应用回调函数动态函数调用函数的间接调用 4.结构体与函数指针结合 1.函数指针定义 函数指针就是一个指向函数的指针变量,与指向数据的指针不同,函数指针保存的是函数的地址,这使得程序可以动态地调用不同的函…...

C语言简要(一)
总得让她开心吧 helloworld #include <stdio.h>int main() {printf("hello world!\n");return 0; } 程序框架 #include <stdio.h> int main {return 0; }输出 printf("hello world!\n"); "里面的内容叫做“字符串”,prin…...

那些年我与c++的叫板(一)--string类自实现
引子:我们学习了c中的string类,那我们能不能像以前数据结构一样自己实现string类呢?以下是cplusplus下的string类,我们参考参考! 废话不多说,直接代码实现:(注意函数之间的复用&…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...
中的KV缓存压缩与动态稀疏注意力机制设计)
大语言模型(LLM)中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型(LLM)参数规模的增长,推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长,而KV缓存的内存消耗可能高达数十GB(例如Llama2-7B处理100K token时需50GB内存&a…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

scikit-learn机器学习
# 同时添加如下代码, 这样每次环境(kernel)启动的时候只要运行下方代码即可: # Also add the following code, # so that every time the environment (kernel) starts, # just run the following code: import sys sys.path.append(/home/aistudio/external-libraries)机…...

spring Security对RBAC及其ABAC的支持使用
RBAC (基于角色的访问控制) RBAC (Role-Based Access Control) 是 Spring Security 中最常用的权限模型,它将权限分配给角色,再将角色分配给用户。 RBAC 核心实现 1. 数据库设计 users roles permissions ------- ------…...

【FTP】ftp文件传输会丢包吗?批量几百个文件传输,有一些文件没有传输完整,如何解决?
FTP(File Transfer Protocol)本身是一个基于 TCP 的协议,理论上不会丢包。但 FTP 文件传输过程中仍可能出现文件不完整、丢失或损坏的情况,主要原因包括: ✅ 一、FTP传输可能“丢包”或文件不完整的原因 原因描述网络…...

链式法则中 复合函数的推导路径 多变量“信息传递路径”
非常好,我们将之前关于偏导数链式法则中不能“约掉”偏导符号的问题,统一使用 二重复合函数: z f ( u ( x , y ) , v ( x , y ) ) \boxed{z f(u(x,y),\ v(x,y))} zf(u(x,y), v(x,y)) 来全面说明。我们会展示其全微分形式(偏导…...
