HNU-算法设计与分析-作业6
第六次作业【分支限界法】

文章目录
- 第六次作业【分支限界法】
- <1> 算法实现题6-2 最小权顶点覆盖问题
- <2> 算法实现题6-6 n后问题
- <3> 算法实现题6-7 布线问题
<1> 算法实现题6-2 最小权顶点覆盖问题
▲问题重述
问题描述:
给定一个赋权无向图 G=(V,E),每个顶点 v∈V 都有一个权值 w(v)。如果 U⊆VU⊆V,且对任意(u,v)∈E 有 u∈U 或 v∈U,就称 U 为图 G 的一个顶点覆盖。G 的最小权顶点覆盖是指 G 中所含顶点权之和最小的顶点覆盖。
算法设计:
对于给定的无向图 G,设计一个优先队列式分支限界法,计算 G 的最小权顶点覆盖。
数据输入:
由文件input.txt给出输入数据。第 1 行有 2 个正整数 n 和 m,表示给定的图 G 有 n 个顶点和 m 条边,顶点编号为 1,2,…,n。第 2 行有 n 个正整数表示 n 个顶点的权。接下来 的 m 行中,每行有 2 个正整数 u,v,表示图 G 的一条边(u,v)。
结果输出:
将计算的最小权顶点覆盖的顶点权之和以及最优解输出到文件output.txt。文件的第1行是最小权顶点覆盖顶点权之和;第2行是最优解xi(1<=i<=n),xi=0表示顶点i不在最小权顶点覆盖中,xi=1表示顶点i在最小权顶点覆盖中。
输入文件示例
input.txt
7 7
1 100 1 1 1 100 10
1 6
2 4
2 5
3 6
4 5
4 6
6 7输出文件示例
output.txt
13
1 0 1 0 1 0 1
▲解题思路
- 定义一个最小堆
MinHeap类,用于实现堆操作。 HeapNode类表示图中的一个顶点。DealNode类包含一些操作,主要是用于处理堆中结点的操作。DealNode::BBVC()方法是该算法的核心部分。通过不断地加入和不加入某个顶点,并通过堆来遍历所有可能的情况,找到图的最小顶点覆盖。MinCover函数是对DealNode::BBVC()方法的封装,用于获取最终的最小顶点覆盖权重。- 在
main函数中,用户输入了图的顶点数vertexNum和边数edgeNum。然后输入每个顶点的权值,并通过边的信息构建了图的邻接矩阵。 - 调用
MinCover函数得到最小顶点覆盖权重,并输出结果。
▲代码
#include <fstream>
#include <iostream>
using namespace std;template <class Type>
class MinHeap // 最小堆类;
{
public:MinHeap(Type a[], int n); // 带两参数的构造函数,在此程序中没有应用;MinHeap(int ms); // 构造函数重载,只初始化堆的大小,对堆中结点不初始化;另外,堆元素的存储是以数组~MinHeap(); // 形式,且无父、子指针,访问父亲结点,利用数组标号进行;bool Insert(const Type &x); // 插入堆中一个元素;bool RemoveMin(Type &x); // 删除堆顶最小结点;void MakeEmpty(); // 使堆为空bool IsEmpty();bool IsFull();int Size();protected:void FilterDown(const int start, const int endOfHeap); // 自顶向下构造堆void FilterUp(const int start); // 自底向上构造堆
private:Type *heap;int maxSize;const int defaultSize;int currentSize; // 堆当前结点个数大小
};template <class Type>
MinHeap<Type>::MinHeap(int ms) : defaultSize(100)
{maxSize = (ms > defaultSize) ? ms : defaultSize;heap = new Type[maxSize];currentSize = 0;
}template <class Type>
MinHeap<Type>::MinHeap(Type a[], int n) : defaultSize(100)
{maxSize = (n > defaultSize) ? n : defaultSize;heap = new Type[maxSize];currentSize = n;for (int i = 0; i < n; i++)heap[i] = a[i];int curPos = (currentSize - 2) / 2;while (curPos >= 0){FilterDown(curPos, currentSize - 1);curPos--;}
}template <class Type>
MinHeap<Type>::~MinHeap()
{delete[] heap;
}template <class Type>
void MinHeap<Type>::FilterDown(const int start, const int endOfHeap)
{int i = start, j = i * 2 + 1;Type temp = heap[i];while (j <= endOfHeap){if (j < endOfHeap && heap[j] > heap[j + 1])j++;if (temp < heap[j])break;else{heap[i] = heap[j];i = j;j = 2 * i + 1;}}heap[i] = temp;
}template <class Type>
void MinHeap<Type>::FilterUp(const int start)
{int i = start, j = (i - 1) / 2;Type temp = heap[i];while (i > 0){if (temp >= heap[j])break;else{heap[i] = heap[j];i = j;j = (i - 1) / 2;}}heap[i] = temp;
}template <class Type>
bool MinHeap<Type>::RemoveMin(Type &x)
{if (IsEmpty()){cerr << "Heap empty!" << endl;return false;}x = heap[0];heap[0] = heap[currentSize - 1];currentSize--;FilterDown(0, currentSize - 1);return true;
}template <class Type>
bool MinHeap<Type>::Insert(const Type &x)
{if (IsFull()){cerr << "Heap Full!" << endl;return false;}heap[currentSize] = x;FilterUp(currentSize);currentSize++;return true;
}template <class Type>
bool MinHeap<Type>::IsEmpty()
{return currentSize == 0;
}template <class Type>
bool MinHeap<Type>::IsFull()
{return currentSize == maxSize;
}template <class Type>
void MinHeap<Type>::MakeEmpty()
{currentSize = 0;
}template <class Type>
int MinHeap<Type>::Size()
{return currentSize;
}// 最小堆结点
class HeapNode // 堆结点类;
{friend class DealNode;public:operator int() const { return cn; }private:int i, // i标示堆中结点号cn, // cn标示当前加入的覆盖顶点中权重之和*x, // x数组标示那些顶点加入了覆盖顶点的行列*c; // c数组标示X中的覆盖顶点中所有的邻接顶点
};// VC类用来对堆中结点内部的的操作
class DealNode
{friend int MinCover(int **, int[], int);private:void BBVC();bool cover(HeapNode E);void AddLiveNode(MinHeap<HeapNode> &H, HeapNode E, int cn, int i, bool ch);int **a, n, *w, *bestx, bestn;
};void DealNode::BBVC()
{// 建立初始空堆MinHeap<HeapNode> H(1000);HeapNode E;E.x = new int[n + 1];E.c = new int[n + 1];for (int j = 1; j <= n; j++){E.x[j] = E.c[j] = 0;}int i = 1, cn = 0;while (true){if (i > n){if (cover(E)){for (int j = 1; j <= n; j++)bestx[j] = E.x[j];bestn = cn;break;}}else{if (!cover(E))AddLiveNode(H, E, cn, i, true); // 加入结点标号为i 的结点到顶点覆盖集中,并把更新后的结点再插入堆中AddLiveNode(H, E, cn, i, false); // 不把结点标号为 i 的结点加入到顶点覆盖集中,并把更新后的结点插入堆中}if (H.IsEmpty())break;H.RemoveMin(E); // 取堆顶点赋给Ecn = E.cn;i = E.i + 1;}
}// 检测图是否被覆盖
bool DealNode::cover(HeapNode E)
{for (int j = 1; j <= n; j++){if (E.x[j] == 0 && E.c[j] == 0) // 存在任意一条边的两个顶点都为0的情况下,为未覆盖情况return false; // X[j]记录覆盖顶点,c[j]记录与覆盖顶点相连的顶点 0表征未覆盖,1表征已覆盖}return true;
}void DealNode::AddLiveNode(MinHeap<HeapNode> &H, HeapNode E, int cn, int i, bool ch)
{HeapNode N;N.x = new int[n + 1];N.c = new int[n + 1];for (int j = 1; j <= n; j++){N.x[j] = E.x[j];N.c[j] = E.c[j];}N.x[i] = ch ? 1 : 0;if (ch){N.cn = cn + w[i]; // 记录i顶点是否加入覆盖的行列中;for (int j = 1; j <= n; j++)if (a[i][j] > 0) // 如果i,j相邻,刚把j顶点加入覆盖邻接顶点集中;N.c[j]++;}else{N.cn = cn;}N.i = i;H.Insert(N); // 插入堆中
}int MinCover(int **a, int v[], int n)
{DealNode Y;Y.w = new int[n + 1];for (int j = 1; j <= n; j++){Y.w[j] = v[j]; // 初始化DealNode类对象Y;}Y.a = a;Y.n = n;Y.bestx = v; // 将地址赋予bestx,Y.BBVC();return Y.bestn; // bestn是最后的最小顶点覆盖集权重;
}int main()
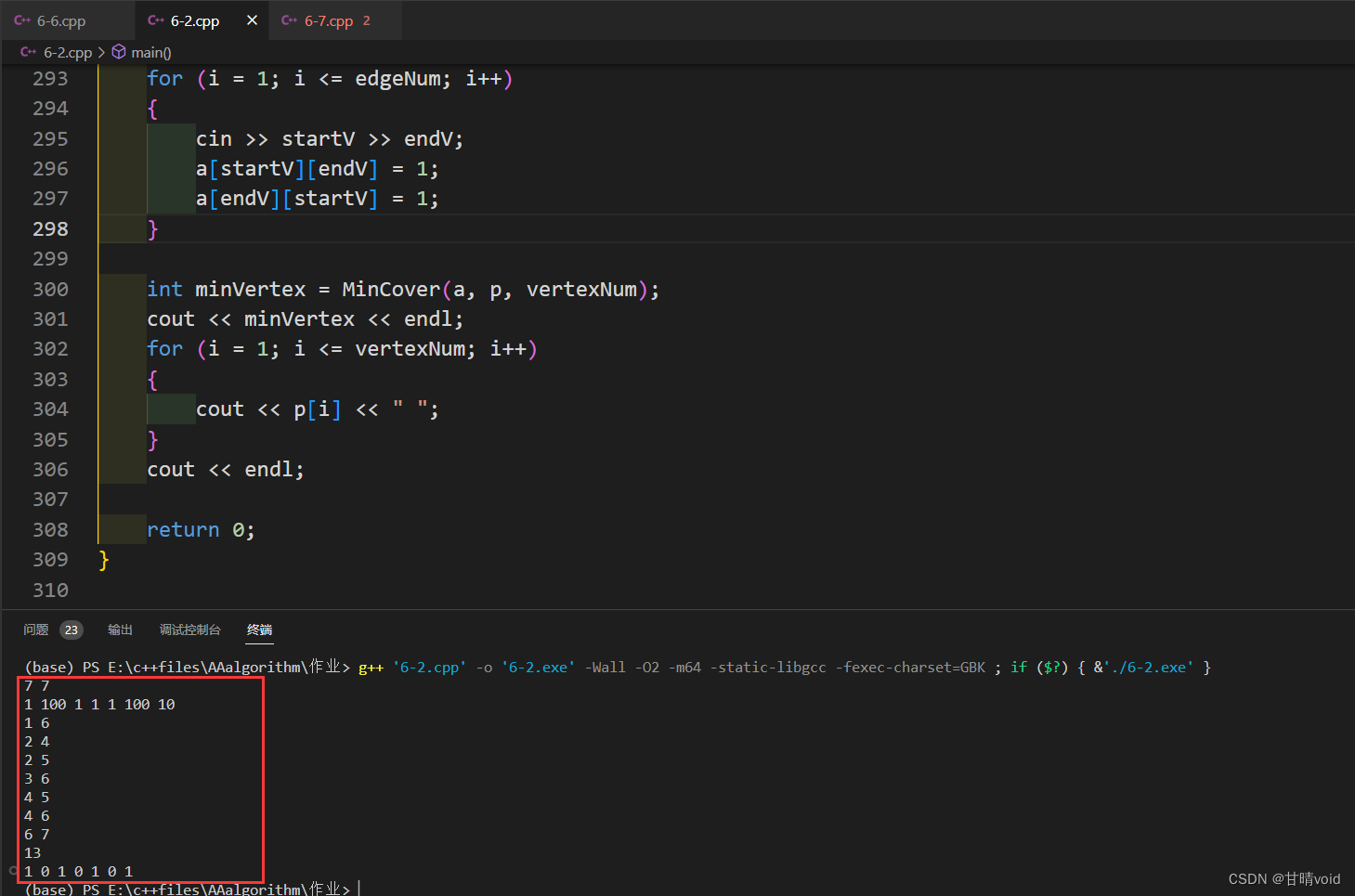
{int startV, endV; // 一条边的起始节点,终止节点int vertexNum, edgeNum; // 顶点数,边数int i;cin >> vertexNum >> edgeNum;int **a; // 图的邻接矩阵表示,1表示有边a = new int *[vertexNum + 1];for (int k = 0; k <= vertexNum; k++)a[k] = new int[vertexNum + 1];for (int i = 0; i <= vertexNum; i++)for (int j = 0; j <= vertexNum; j++)a[i][i] = 0;int *p; // 顶点的权值数组p = new int[vertexNum + 1];for (i = 1; i <= vertexNum; i++)cin >> p[i];for (i = 1; i <= edgeNum; i++){cin >> startV >> endV;a[startV][endV] = 1;a[endV][startV] = 1;}int minVertex = MinCover(a, p, vertexNum);cout << minVertex << endl;for (i = 1; i <= vertexNum; i++){cout << p[i] << " ";}cout << endl;return 0;
}▲验证
<2> 算法实现题6-6 n后问题
▲问题重述
设计一个解n后问题的队列式分支限界法,计算在n × n n\times nn×n个方格上放置彼此不受攻击的n个皇后的一个放置方案。
案例
input
5
output
1 3 5 2 4
▲解题思路
- 定义一个结构体
node,表示棋盘上的每一个可能的位置,以及记录了当前状态的一些信息,如列、左右对角线等的占用情况。 - 使用优先队列
priority_queue来存储搜索过程中的状态,按照结构体中的x值进行排序。这里的x表示当前放置的皇后所在的行数。 - 在主循环中,初始化棋盘的初始状态,将第一行的每一个位置作为起点,生成相应的初始状态,并加入优先队列中。
- 进入主循环,每次从优先队列中取出一个状态,判断是否达到了目标状态(即放置了所有皇后),如果是则输出解,并结束程序(因为只需要找到一个可行解即可)。
- 如果当前状态不是目标状态,继续在下一行尝试放置皇后。遍历每一列,对于每一个可行的位置,生成新的状态并加入优先队列中。
- 在生成新状态时,进行剪枝操作,检查当前位置是否与之前的皇后冲突,如果冲突则跳过该位置。
- 重复以上步骤,直到找到一个解或者队列为空。由于采用优先队列,搜索时会先尝试最有希望的位置,加速找到解的过程。
▲代码
#include <bits/stdc++.h>
using namespace std;
#define N 100
int n;
struct node
{int vis[N] = {0}, col[N] = {0}, lr[N] = {0}, rl[N] = {0};int x, y;node(int a, int b) : x(a), y(b) {}bool operator<(const node &a) const{return x < a.x;}
};
priority_queue<node> q;
int main()
{cin >> n;for (int i = 0; i < n; i++){node temp = node(0, i);temp.vis[0] = i + 1;temp.col[i] = 1;temp.rl[temp.x + temp.y] = 1;temp.lr[50 + temp.x - temp.y] = 1;q.push(temp);}while (!q.empty()){node temp = q.top();q.pop();if (temp.x == n - 1){for (int i = 0; i < n; i++){cout << temp.vis[i] << " ";}cout << endl;break; // 只需要给出一个答案即可}if (temp.x < n - 1){for (int i = 0; i < n; i++){node next = node(temp.x + 1, i);if (temp.col[next.y] || temp.lr[50 + next.x - next.y] || temp.rl[next.x + next.y]){ // 剪枝continue;}for (int i = 0; i < N; i++){next.lr[i] = temp.lr[i];next.rl[i] = temp.rl[i];next.col[i] = temp.col[i];}next.col[next.y] = 1;next.lr[50 + next.x - next.y] = 1;next.rl[next.x + next.y] = 1;for (int i = 0; i < next.x; i++){next.vis[i] = temp.vis[i];}next.vis[next.x] = i + 1;q.push(next);}}}return 0;
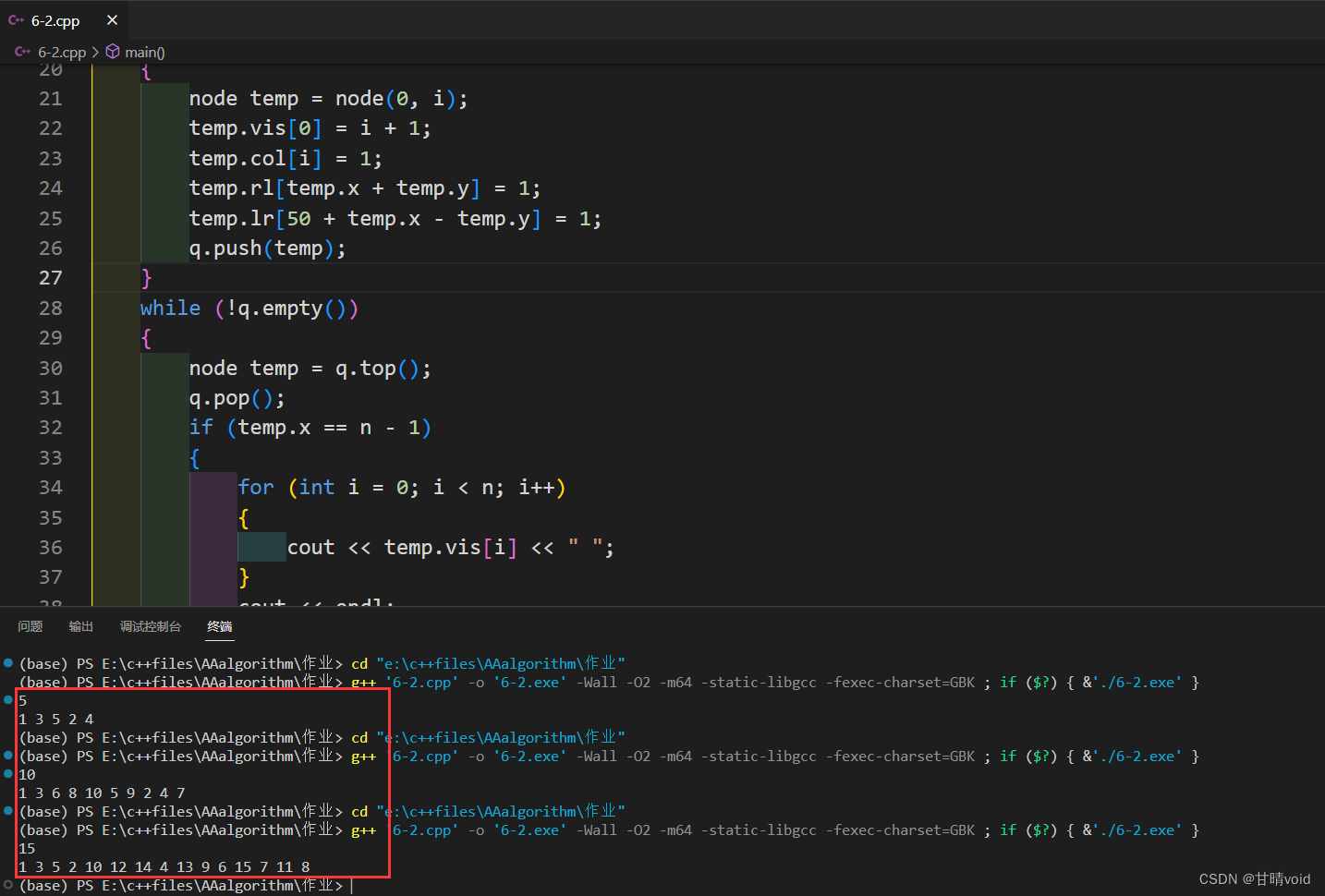
}▲验证
验证了n=5,10,15三种情况。
<3> 算法实现题6-7 布线问题
▲问题重述

▲解题思路
MinHeap类定义了最小堆,用于存储待处理的状态。该堆的元素是BoardNode类型的对象。BoardNode类表示电路板的一种摆放方式,包含了一些必要的信息。len方法用于计算电路板摆放的长度。BBArrangeBoards函数是基于分支限界法的核心算法。它通过不断生成摆放状态,使用最小堆来搜索可能的最优解。HeapSize为堆的大小。Make2DArray函数用于动态创建二维数组。- 在
main函数中,用户输入了电路板数量n。通过Make2DArray创建了二维数组B,表示电路板之间的连接关系。然后调用BBArrangeBoards函数求解问题,并输出最小长度和对应的摆放方式。
▲代码
#include <array>
#include <bits/stdc++.h>
#include <queue>
using namespace std;
int n, *p;
template <class Type>
class MinHeap // 最小堆类;
{
public:MinHeap(Type a[], int n); // 带两参数的构造函数,在此程序中没有应用;MinHeap(int ms); // 构造函数重载,只初始化堆的大小,对堆中结点不初始化;另外,堆元素的存储是以数组~MinHeap(); // 形式,且无父、子指针,访问父亲结点,利用数组标号进行;bool Insert(const Type &x); // 插入堆中一个元素;bool RemoveMin(Type &x); // 删除堆顶最小结点;void MakeEmpty(); // 使堆为空bool IsEmpty();bool IsFull();int Size();protected:void FilterDown(const int start, const int endOfHeap); // 自顶向下构造堆void FilterUp(const int start); // 自底向上构造堆
private:Type *heap;int maxSize;const int defaultSize;int currentSize; // 堆当前结点个数大小
};template <class Type>
MinHeap<Type>::MinHeap(int ms) : defaultSize(100)
{maxSize = (ms > defaultSize) ? ms : defaultSize;heap = new Type[maxSize];currentSize = 0;
}template <class Type>
MinHeap<Type>::MinHeap(Type a[], int n) : defaultSize(100)
{maxSize = (n > defaultSize) ? n : defaultSize;heap = new Type[maxSize];currentSize = n;for (int i = 0; i < n; i++)heap[i] = a[i];int curPos = (currentSize - 2) / 2;while (curPos >= 0){FilterDown(curPos, currentSize - 1);curPos--;}
}template <class Type>
MinHeap<Type>::~MinHeap()
{delete[] heap;
}template <class Type>
void MinHeap<Type>::FilterDown(const int start, const int endOfHeap)
{int i = start, j = i * 2 + 1;Type temp = heap[i];while (j <= endOfHeap){if (j < endOfHeap && heap[j] > heap[j + 1])j++;if (temp < heap[j])break;else{heap[i] = heap[j];i = j;j = 2 * i + 1;}}heap[i] = temp;
}template <class Type>
void MinHeap<Type>::FilterUp(const int start)
{int i = start, j = (i - 1) / 2;Type temp = heap[i];while (i > 0){if (temp >= heap[j])break;else{heap[i] = heap[j];i = j;j = (i - 1) / 2;}}heap[i] = temp;
}template <class Type>
bool MinHeap<Type>::RemoveMin(Type &x)
{if (IsEmpty()){cerr << "Heap empty!" << endl;return false;}x = heap[0];heap[0] = heap[currentSize - 1];currentSize--;FilterDown(0, currentSize - 1);return true;
}template <class Type>
bool MinHeap<Type>::Insert(const Type &x)
{if (IsFull()){cerr << "Heap Full!" << endl;return false;}heap[currentSize] = x;FilterUp(currentSize);currentSize++;return true;
}template <class Type>
bool MinHeap<Type>::IsEmpty()
{return currentSize == 0;
}template <class Type>
bool MinHeap<Type>::IsFull()
{return currentSize == maxSize;
}template <class Type>
void MinHeap<Type>::MakeEmpty()
{currentSize = 0;
}template <class Type>
int MinHeap<Type>::Size()
{return currentSize;
}class BoardNode
{friend int BBArrangeBoards(int **, int, int *&);public:operator int() const { return cd; }int len(int **, int ii);private:int *x, s, cd;
};int BoardNode::len(int **conn, int ii)
{int sum = 0;for (int i = 1, sum = 0; i <= ii; i++){for (int j = i + 1; j <= ii; j++){int dist = x[i] > x[j] ? x[i] - x[j] : x[j] - x[i];sum += conn[i][j] * dist;}}return sum;
}int BBArrangeBoards(int **conn, int n, int *&bestx)
{int HeapSize = 10;MinHeap<BoardNode>H(HeapSize);BoardNode E;E.x = new int[n + 1];E.s = 0;E.cd = 0;for (int i = 1; i <= n; i++)E.x[i] = i;int bestd = INT_MAX;bestx = 0;while (E.cd < bestd){if (E.s == n - 1){int ld = E.len(conn, n);if (ld < bestd){delete[] bestx;bestx = E.x;bestd = ld;}elsedelete[] E.x;}else{for (int i = E.s + 1; i <= n; i++){BoardNode N;N.x = new int[n + 1];N.s = E.s + 1;for (int j = 1; j <= n; j++)N.x[j] = E.x[j];N.x[N.s] = E.x[i];N.x[i] = E.x[N.s];N.cd = N.len(conn, N.s);if (N.cd < bestd)H.Insert(N);elsedelete[] N.x;}}delete[] E.x;}try{H.RemoveMin(E);}catch (...){return bestd;}while (true){delete[] E.x;try{H.RemoveMin(E);}catch (...){break;}}return bestd;
}template <class T>
void Make2DArray(T **&x, int rows, int cols)
{x = new T *[rows];for (int i = 0; i < rows; ++i){x[i] = new T[cols];}
}int main()
{cin >> n;p = new int[n + 1];int **B;Make2DArray(B, n + 1, n + 1);for (int i = 1; i <= n - 1; i++)for (int j = i + 1; j <= n; j++)cin >> B[i][j];cout << BBArrangeBoards(B, n, p) << endl;for (int i = 1; i <= n; i++)cout << p[i] << " ";cout << endl;return 0;
}▲验证
书上案例验证通过。
相关文章:

HNU-算法设计与分析-作业6
第六次作业【分支限界法】 文章目录 第六次作业【分支限界法】<1> 算法实现题6-2 最小权顶点覆盖问题<2> 算法实现题6-6 n后问题<3> 算法实现题6-7 布线问题 <1> 算法实现题6-2 最小权顶点覆盖问题 ▲问题重述 问题描述: 给定一个赋权无向…...

2D Chests Assets - Mega Pack
科幻/奇幻/经典主题的箱子和容器。AAA质量,高分辨率,VFX,源PSD文件。 这是一个带有手绘套装的大包装: -【梦幻之栗】 -【科幻钱包】 AAA质量。高分辨率。一切都已准备就绪,可供使用。包括PSD文件。 在1.1版本中添加了VFX并将项目更新为URP。请注意,新的VFX仅适用于URP/HD…...
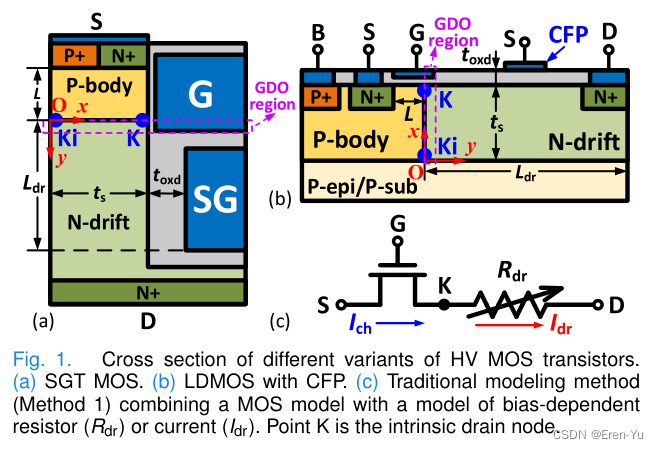
一种基于电场连续性的高压MOSFET紧凑模型,用于精确表征电容特性
来源:A Compact Model of High-Voltage MOSFET Based on Electric Field Continuity for Accurate Characterization of Capacitance(TED 24年) 摘要 本文提出了一种新的高压MOSFET(HV MOS)紧凑模型,以消…...

vue阶段性测试题,内容丰富,案例典型,题目配有答案
阶段性测试 理论题实践题 1)理论题 请简述Vue、Node.js、Vscode是什么,以及有什么关系 1. vue是一个轻量级、比较灵活的且支持组件开发的网络框架 2. node.js是让JavaScript运行在服务器上的一直环境 3. Vscode是一款有着丰富插件的代码编辑器 4. 关系…...
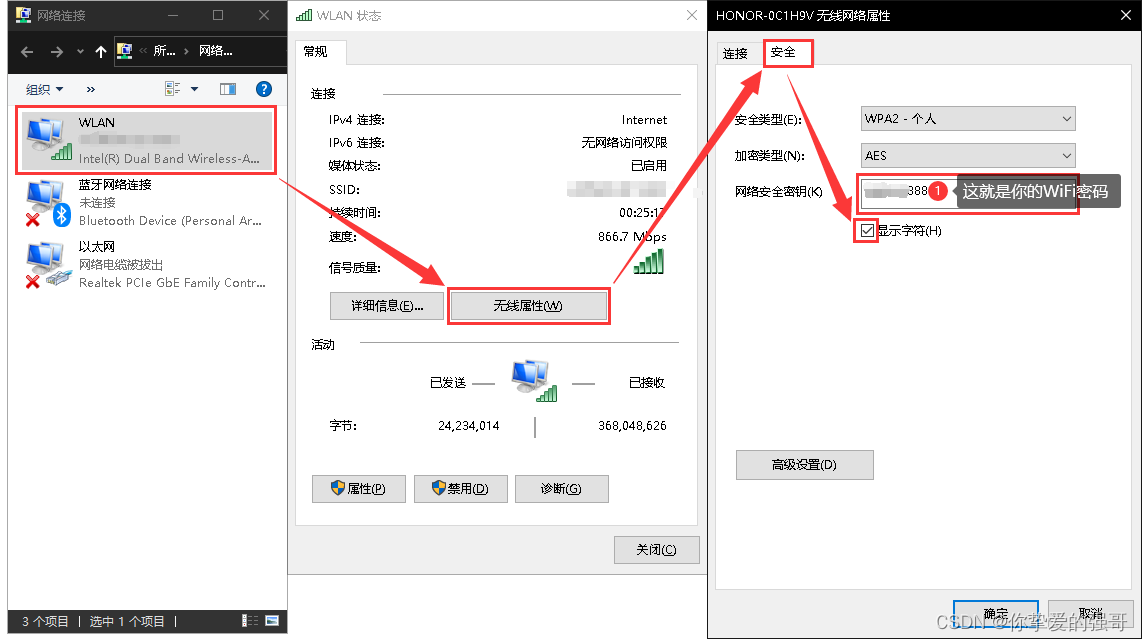
如何查看PC电脑已经已经连接上的网络WiFi密码?
运行ncpa.cpl...

Java 语言的特点分析及应用
Java语言自问世以来,因其独特的设计理念和广泛的应用领域,成为了编程语言中的一颗璀璨明星。以下是对Java语言特点的详细分析及其实际应用场景,希望能帮助面试者更好地理解和掌握Java的优势。 1. 简单易学 Java的语法简单,类似于…...
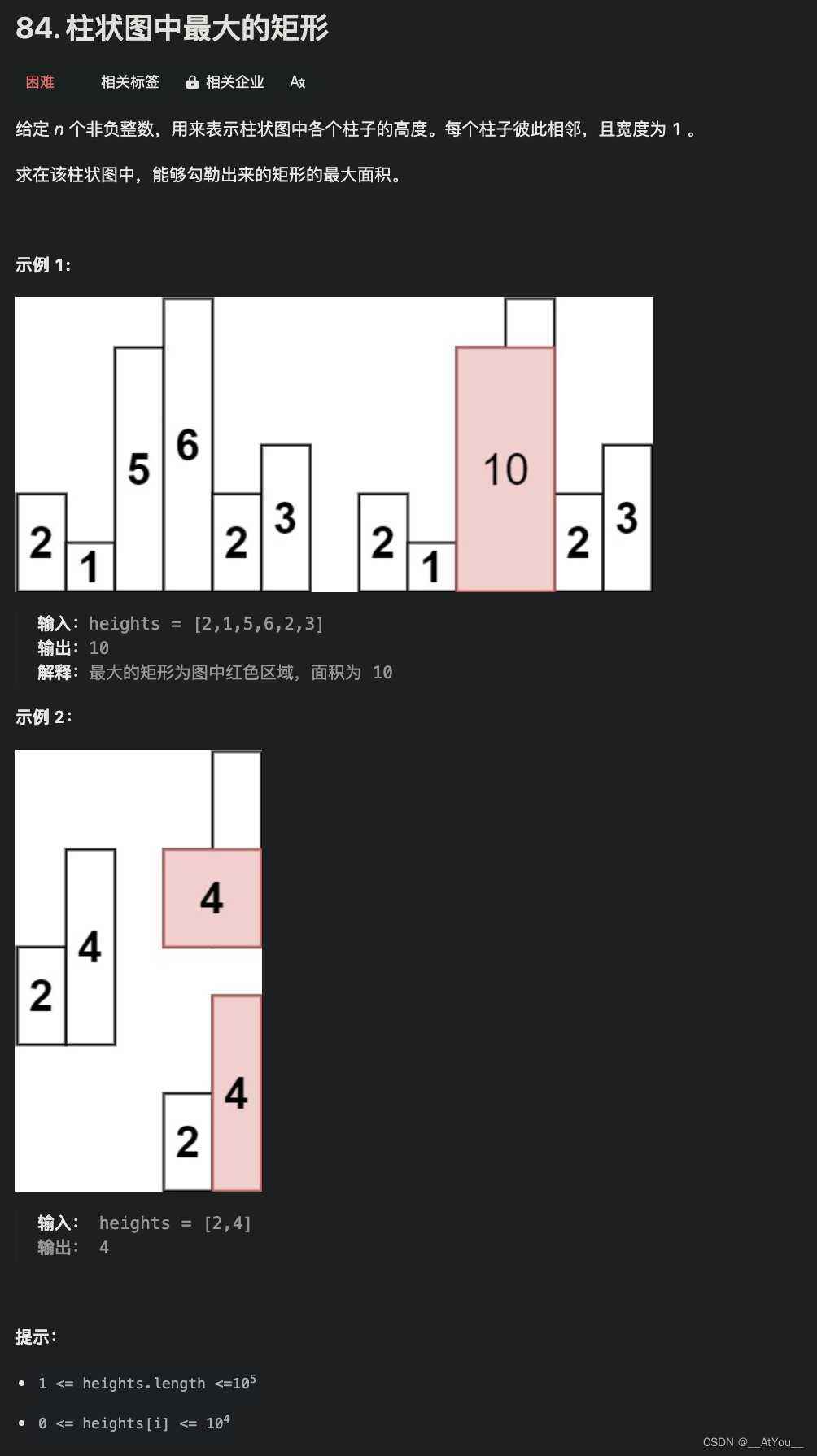
Golang | Leetcode Golang题解之第84题柱状图中最大的矩形
题目: 题解: func largestRectangleArea(heights []int) int {n : len(heights)left, right : make([]int, n), make([]int, n)for i : 0; i < n; i {right[i] n}mono_stack : []int{}for i : 0; i < n; i {for len(mono_stack) > 0 &&am…...
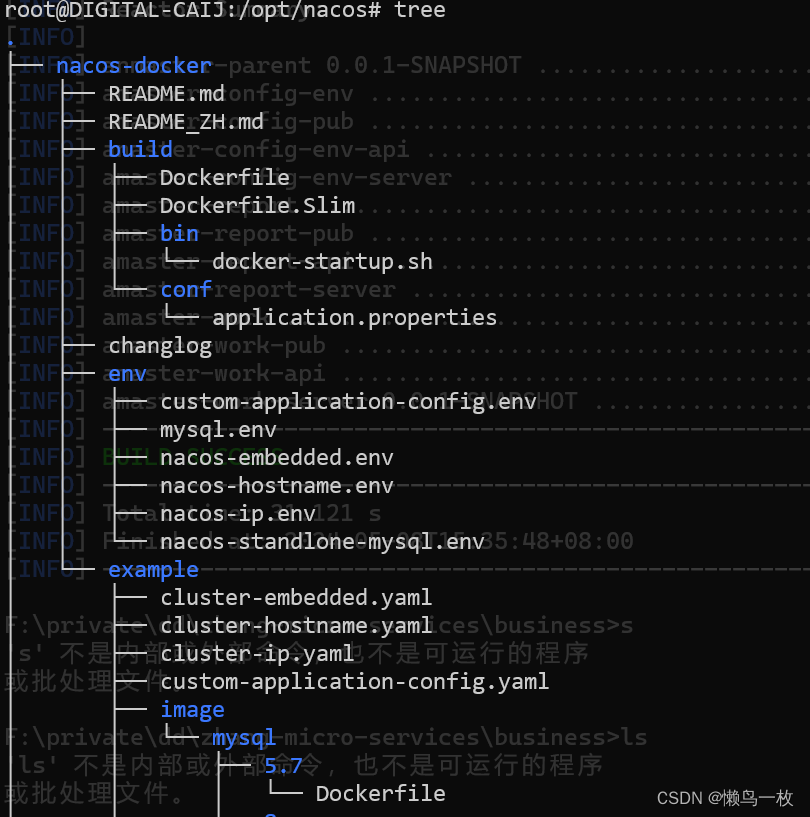
linux实用命令
一、常用命令 mkdir -p mkdir -p 命令用于在Unix和Linux系统中创建目录。其中,-p参数确保目录名称存在,如果目录不存在的就新创建一个。换句话说,-p参数允许创建一个目录和它不存在的父目录,确保了指定的整个目录路径都会被…...

创建和管理数据库
1. 一条数据的存储过程 存储数据是处理数据的第一步.只有正确的把数据存储起来,我们才能进行有效的处理和分析.否则,只能是一团乱麻.在MySQL中,一个完整的数据存储过程一共有四步 : 创建数据库,确认字段,创建数据表&a…...

Spring STOMP-发送消息
如果你想要从应用程序的任何地方向连接的客户端发送消息,要怎么做?任何应用程序组件都可以向brokerChannel发送消息。要这样做,最简单方法是注入一个SimpMessagingTemplate并使用它来发送消息。通常,你会按类型注入它,…...

kubernetes多master集群架构
一、完成master02节点的初始化操作 master02环境准备,详细过程参考上一期博客环境准备 #添加主机映射 vim /etc/hosts 192.168.88.3 master01 192.168.88.8 master02 192.168.88.4 node01 192.168.88.5 node021、准备master02节点需要的文件 从 master01 节点上拷…...
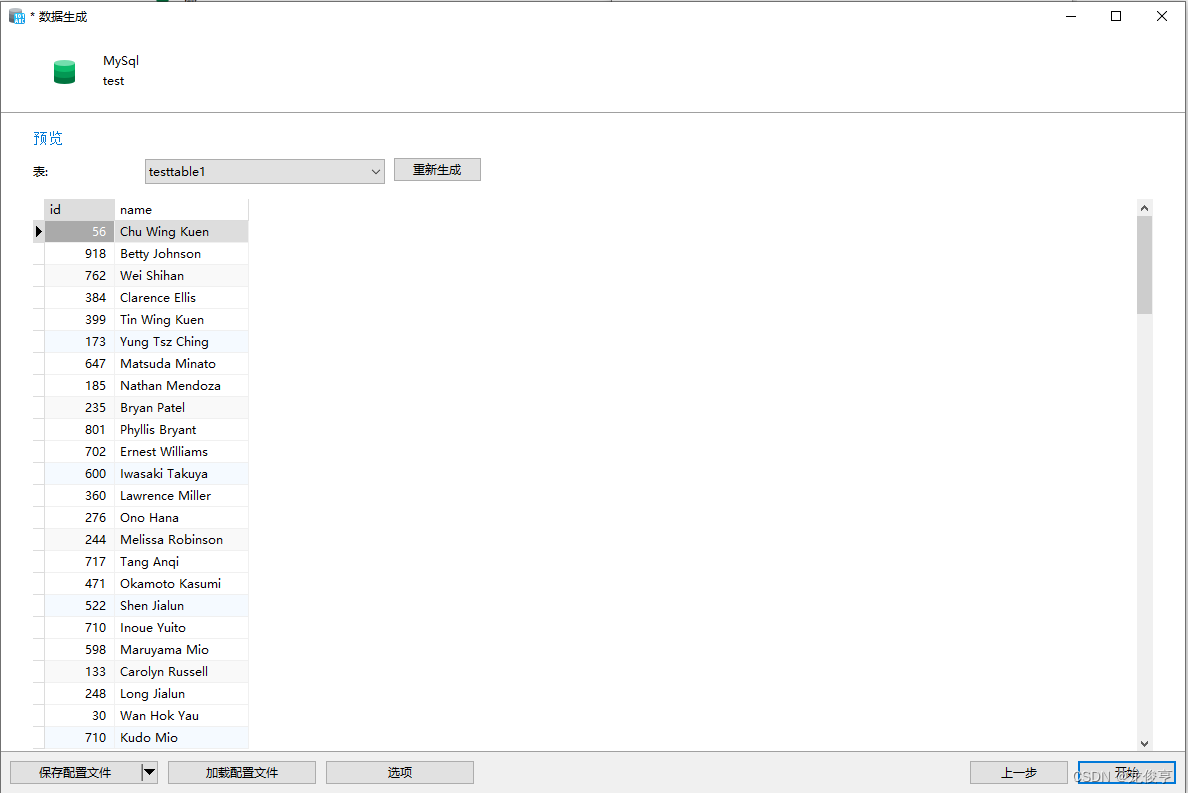
MySQL数据库的初始化(创建库、创建表、向数据库添加测试数据)
MySQL数据库的初始化(创建库、创建表、修改数据库访问密码、向数据库添加测试数据) MySQL数据库简介MySQL创建一个新的数据库修改数据库访问密码 MySQL创建一张新的数据表简单(设置)表复杂(设置)表 填充测试…...

hive动态分区
hive动态分区概念:允许插入数据到分区表时,根据插入的数据内容自动创建相应的分区 1.启用动态分区功能 hive.exec.dynamic.partitiontrue; 2.分区字段设置 在insert语句中, 动态分区的字段必须放在select语句的末尾,hive会根据这个字段的值来创建分区目录 示例: --创建分区表…...
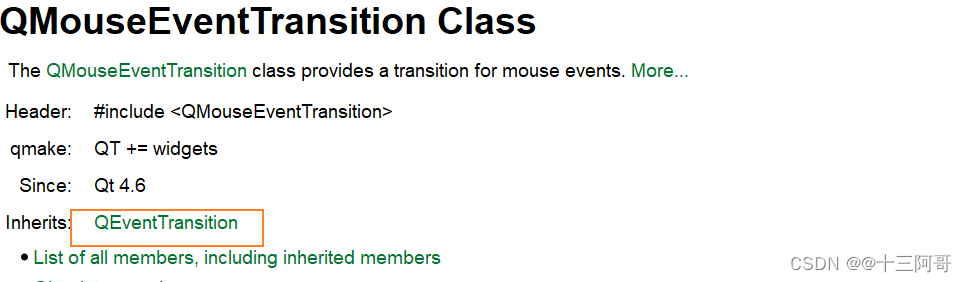
QT状态机10-QKeyEventTransition和QMouseEventTransition的使用
1、QMouseEventTransition的使用 首先明白 QMouseEventTransition 继承自 QEventTransition类。 关于QEventTransition类的使用,可参考 QT状态机9-QEventTransition和QSignalTransition的使用 回顾 QT状态机9-QEventTransition和QSignalTransition的使用 中的状态切换代码,如…...

PDK安装及简介
目录 PDK简介 pdk安装 Standard Cell Library简介 IO Library简介 PDK简介 PDK:全称Process Design Kit,是工艺设计工具包的缩写,是制造和设计之间的沟通桥梁,是模拟电路设计的起始点。 具体来说,PDK是代工厂(FAB…...
20240511每日运维----聊聊nignx改配置所有的nginx改完unknow
1、改配置所有的nginx改完unknow src/core/nginx.h src/http/ngx_http_header_filter_module.c src/http/ngx_http_special_response.c src/http/v2/ngx_http_v2_filter_module.c 2、make 3、去objs里面把nginx文件替换过去sbin/nginx...

hive日常使用时忘记部分补充(不定时)
1、date_formate、unix_timestamp、from_unixtime用法: 2、lag()、lead()用法: lag()窗口函数返回分区中当前行之前行(可以指定第几行)的值。 如果没有行,则返回null。 lead()窗口…...

android 安全机制 和权限管理 的一点研究
Android 应用权限设置: 在 Android 中,每个应用都必须声明其需要的权限,例如访问相机、读取联系人等。这些权限在应用安装时由用户授予,并且用户可以在应用运行时随时更改这些权限。Android 的权限模型是基于用户授予或拒绝应用对敏感资源的访问。这种模型允许用户在应用级…...

Vue3.0 一些总结 【持续更新】
1. reactive 只适用于对象 (包括数组和内置类型,如 Map 和 Set,它不支持如 string、number 或 boolean 这样的原始类型) import { reactive } from vueconst counter reactive({count: 0 })console.log(counter.count) // 0 counter.count注意…...

C++语法|对象的浅拷贝和深拷贝
背景: 我们手写一个顺序栈,展开接下来的实验: ⭐️ this指针指向的是类在内存中的起始位置 class SeqStack { public:SqeStack(int size 10) {cout << this << "SeqStack()" << endl;pstack_ new int[size_];t…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...
