[Algorithm][回溯][字母大小写全排列][优美的排列][N皇后]详细讲解
目录
- 1.字母大小写全排列
- 1.题目链接
- 2.算法原理详解
- 3.代码实现
- 2.优美的排列
- 1.题目链接
- 2.算法原理详解
- 3.代码实现
- 3.N 皇后
- 1.题目链接
- 2.算法原理详解
- 3.代码实现
1.字母大小写全排列
1.题目链接
- 字母大小写全排列
2.算法原理详解
- 本题逻辑与子集大致相同
-
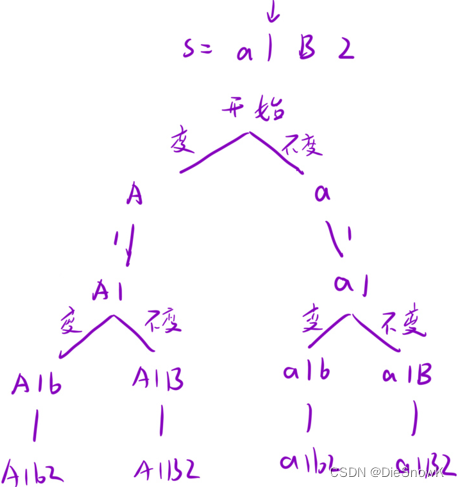
- 思路一:每次盯着一个字符,变或是不变
- 全局变量:
string pathvector<string> ret
DFS()设计- 函数头:
void DFS(string, pos)pos:下一层递归要选的元素
- 函数体:
- 字母可能变/不变,数字一定不需要变
- 递归出口:
pos == nums.size()
- 函数头:
- 回溯:变完函数返回时需要回溯
- 全局变量:
- 思路一:每次盯着一个字符,变或是不变
3.代码实现
class Solution
{string path;vector<string> ret;
public:vector<string> letterCasePermutation(string s) {DFS(s, 0);return ret;}void DFS(string& s, int pos){if(pos == s.size()){ret.push_back(path);return;}char ch = s[pos];// 不改变path += ch;DFS(s, pos + 1);path.pop_back(); // 回溯,恢复现场// 改变if(ch < '0' || ch > '9'){ch = Change(ch);path += ch;DFS(s, pos + 1);path.pop_back(); // 回溯,恢复现场}}char Change(char ch){if(ch >= 'a' && ch <= 'z'){ch -= 32;}else{ch += 32;}return ch;}
};
2.优美的排列
1.题目链接
- 优美的排列
2.算法原理详解
- 思路:对每个位置挨个尝试填入数字
- 全局变量:
int retvector<bool> check-> 剪枝
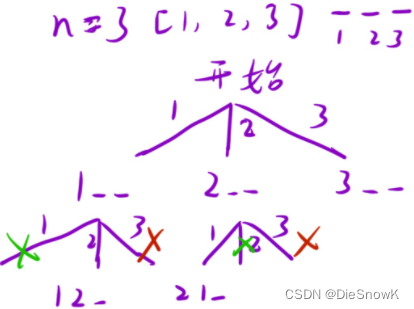
DFS()设计:void DFS(pos, n)- 剪枝:
- 之前用过的数字不再使用
- 不符合情况的不填入
- 回溯:每层递归返回时回溯
- 全局变量:
3.代码实现
class Solution
{int ret = 0;vector<bool> check;
public:int countArrangement(int n) {check.resize(n + 1, false);DFS(1, n);return ret;}void DFS(int pos, int n){if(pos == n + 1){ret++;return;}for(int i = 1; i <= n; i++){if(!check[i] && (i % pos == 0 || pos % i == 0)){check[i] = true;DFS(pos + 1, n);check[i] = false; // 回溯,恢复现场}}}
};
3.N 皇后
1.题目链接
- N 皇后
2.算法原理详解
-
本题可以学习二维数组判断行列、主副对角线是否放有数据
-
思路:在每一行找合适的列放置皇后,即每次枚举都是枚举一行
-DFS()设计:void DFS(row)- 决策树
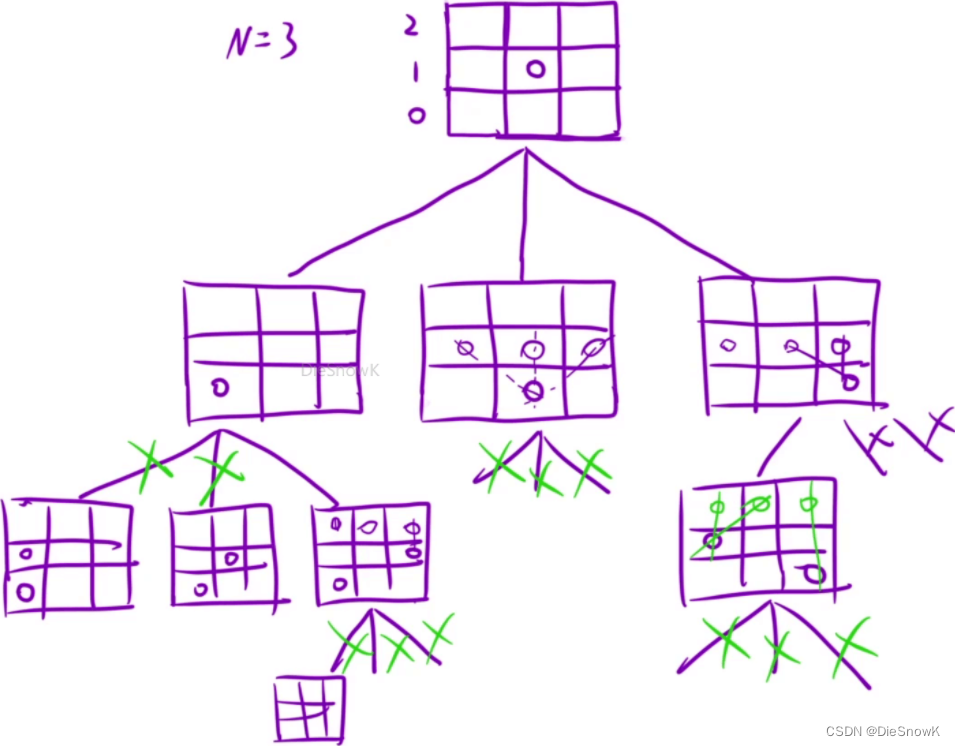
- 决策树
-
如何剪枝?-> 当前这个位置,能否放上皇后?
- 无脑四个循环判断行列、主副对角线 -> ×
- 类似哈希表的策略,需要一定数学理解
- 行不需要剪枝,收递归限制
bool checkCol[n]-> 判断列- 对应下标表示每列是否放置过皇后
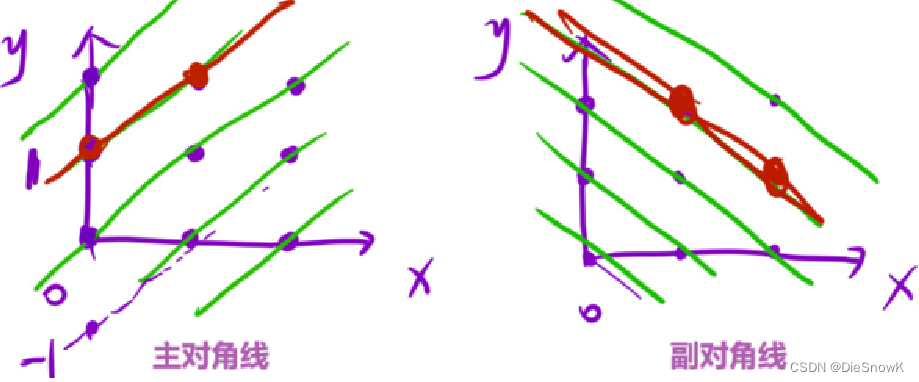
bool checkDig1[2 * n]-> 主对角线y = x + b->y - x = b->b可以唯一标识一个对角线y - x + n = b + n-> 两边加上一个固有偏移量防止下标出现负数
bool checkDig2[2 * n]-> 副对角线y = -x + b->y + x = b->b可以唯一标识一个对角线- 副对角线不需要固定偏移量,因为副对角线的纵截距都大于0
3.代码实现
class Solution
{int _n = 0;vector<bool> checkCol;vector<bool> checkDig1;vector<bool> checkDig2;vector<vector<string>> ret;vector<string> path;
public:vector<vector<string>> solveNQueens(int n) {_n = n;checkCol.resize(n, false);checkDig1.resize(2 * n, false);checkDig2.resize(2 * n, false);path.resize(n, string(n, '.'));DFS(0);return ret;}void DFS(int row){// 递归出口if(row == _n){ret.push_back(path);return;}// 对于每一行,枚举每一列for(int i = 0; i < _n; i++){// 剪枝if(!checkCol[i] && !checkDig1[row - i + _n] && !checkDig2[row + i]){checkCol[i] = checkDig1[row - i + _n] = checkDig2[row + i] = true;path[row][i] = 'Q';DFS(row + 1);checkCol[i] = checkDig1[row - i + _n] = checkDig2[row + i] = false; // 回溯path[row][i] = '.';}}}
};
相关文章:

[Algorithm][回溯][字母大小写全排列][优美的排列][N皇后]详细讲解
目录 1.字母大小写全排列1.题目链接2.算法原理详解3.代码实现 2.优美的排列1.题目链接2.算法原理详解3.代码实现 3.N 皇后1.题目链接2.算法原理详解3.代码实现 1.字母大小写全排列 1.题目链接 字母大小写全排列 2.算法原理详解 本题逻辑与子集大致相同 思路一:每…...

.NET_NLog
步骤 1. 添加依赖 ①Microsoft.Extensions.DependencyInjection ②NLog.Extensions.Logging(或Microsoft.Extensions.Logging.___) Tutorial NLog/NLog Wiki GitHub 2.添加nlog.config文件(默认名称, 可改为其他名称, 但需要另行配置) 文件的基础…...

Linux查看进程命令ps和top
Linux 是一种自由和开放源代码的操作系统,它的使用在全球范围内非常广泛。在 Linux 中,进程是操作系统中最重要的组成部分之一,它代表了正在运行的程序。了解如何查看正在运行的进程是非常重要的,因为它可以帮助你了解系统的运行状…...
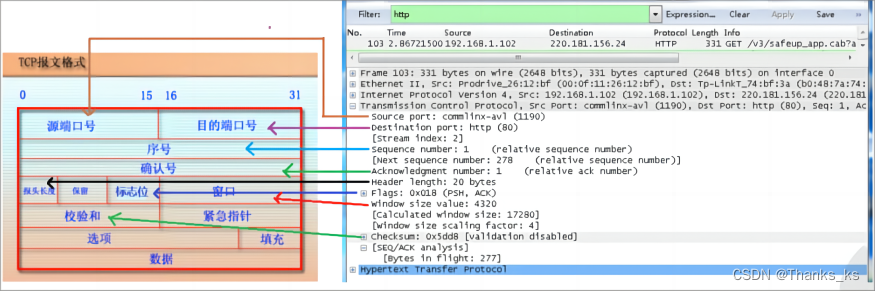
深入解析Wireshark1:从捕获到分析,一网打尽数据包之旅
目录 1 认识 Wireshark 1.1 选择网卡界面 1.2 捕获数据包界面 1.3 常用按钮功能介绍 1.4 数据包列表信息 1.5 数据包详细信息 2 数据包案例分析 Frame: 物理层的数据帧概况 Ethernet II: 数据链路层以太网帧头部信息 Internet Protocol Version 4 (IPv4): 互联网层IP…...
的指针及其相关应用场景)
C++语法|指向类成员(成员变量和成员方法)的指针及其相关应用场景
文章目录 1.基本语法指向成员变量的指针示例 指向成员函数的指针示例 注意事项 2.应用场景泛型编程和模板:通用成员访问打印函数回调机制和事件处理:基于简单GUI框架的事件处理 1.基本语法 指向类成员的指针是一种特殊的指针类型,用于指向类…...
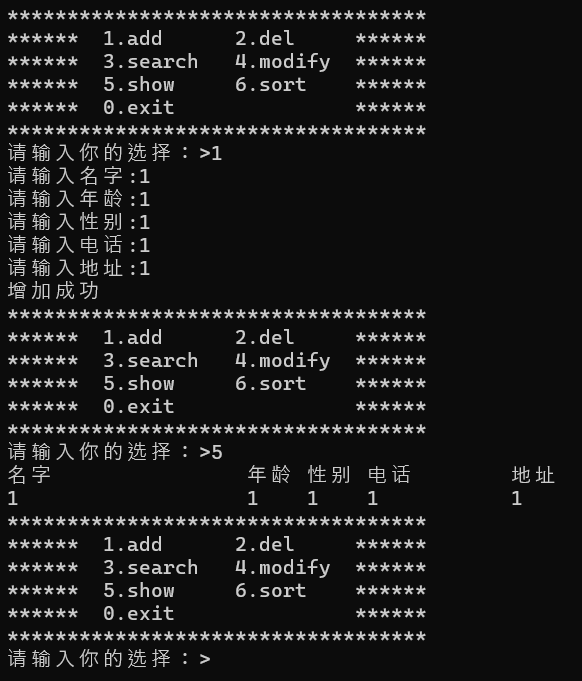
【C语言】通讯录系统实现
目录 1、通讯录系统介绍 2、代码分装 3、代码实现步骤 3.1制作菜单函数以及游戏运行逻辑流程 3.2、封装人的信息PeoInfo以及通讯录Contact结构体类型 3.3、初始化通讯录InitContact函数 3.4、增加联系人AddContact函数 3.5、显示所有联系人ShowContact函数 3.6、删除联系人D…...
 Object Pascal 学习笔记---第12章第1节 ( 类静态方法与Windows API回调))
(delphi11最新学习资料) Object Pascal 学习笔记---第12章第1节 ( 类静态方法与Windows API回调)
12.1.4 类静态方法与Windows API回调 静态类方法没有隐藏的Self参数意味着静态类方法可以作为回调函数传递给操作系统(例如,在Windows上)。实际上,您可以声明一个具有stdcall调用约定的静态类方法,并将其用作直接的…...

第一个Rust程序
在安装好Rust以后,我们就可以编写程序了。 首先,我们执行下面的命令,尽量让你的rust版本和我的版本相同,或者比我的版本大。 zhangdapengzhangdapeng:~$ cargo --version cargo 1.78.0 (54d8815d0 2024-03-26) zhangdapengzhangd…...

【LInux】<基础IO> 文件操作 | 文件描述符 | 重定向
👦个人主页:Weraphael ✍🏻作者简介:目前正在学习c和算法 ✈️专栏:Linux 🐋 希望大家多多支持,咱一起进步!😁 如果文章有啥瑕疵,希望大佬指点一二 如果文章对…...

MySQL--增、删、改、查,
数据库的概述、发展、现状、历史、分类 MySQL关系型数据库、架构(C/S) window系统安装MySQL数据库 Linux系统【选学】 数据库对象——数据库(database) show、create、drop命令 数据库对象——表(tableÿ…...
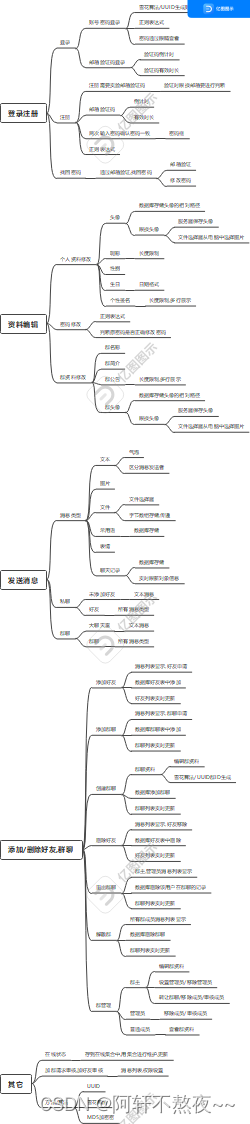
5.12学习总结
一.JAVA聊天室项目 文件发送 使用 Java Socket 实现聊天内容或文件的传输的原理如下: 服务器端启动:聊天室的服务器端在指定的端口上监听客户端的连接。它创建一个 ServerSocket 对象,并通过调用 accept() 方法等待客户端的连接请求。客户…...
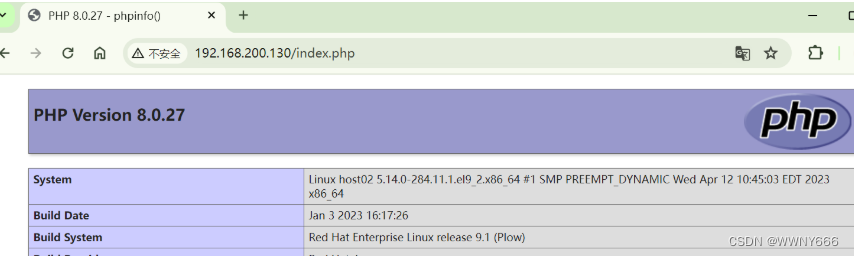
ansible利用playbook 部署lamp架构
搭建参考:ansible批量运维管理-CSDN博客 定义ansible主机清单 [rootansible-server ~]# vim /etc/hosts 192.168.200.129 host01 192.168.200.130 host02 [rootansible-server ~]# vim /etc/ansible/hosts [webserver] host01 host02 在ansible端编写index.html…...
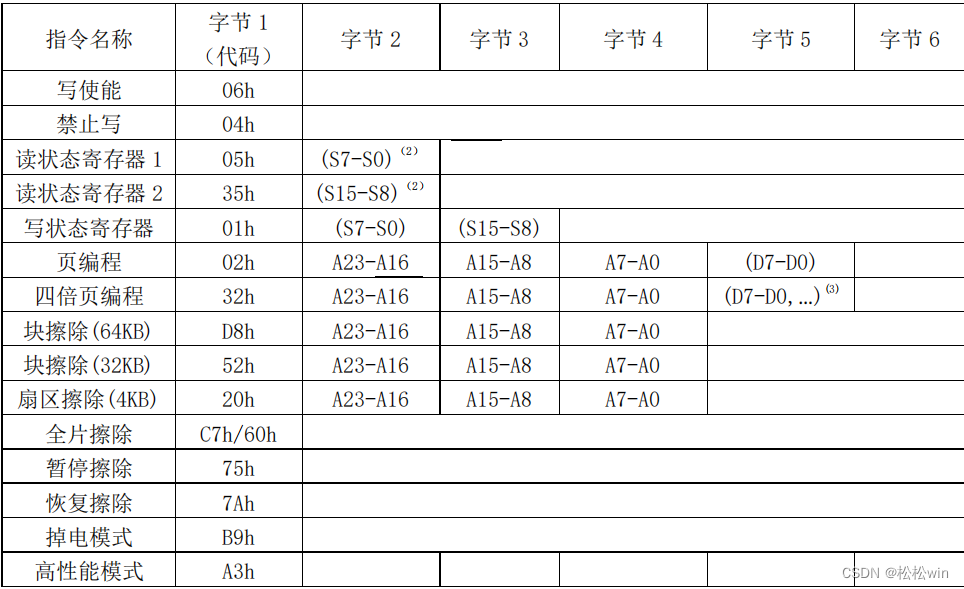
SPI通信(使用SPI读写W25Q64)
SPI通信协议 • SPI(Serial Peripheral Interface)是由Motorola公司开发的一种通用数据总线 • 四根通信线: SCLK:串行时钟线,用来提供时钟信号的。 MOSI:主机输出,从机输入 MISO:从机输出,主机输入 SS:…...

<sa8650>QCX Usecase 使用详解—拓扑图 XML 定义
<sa8650>QCX Usecase 使用详解—拓扑图 XML 定义 一 、前言二、拓扑图 XML 定义2.1 <Node, port, link>2.2 < XML prolog >2.3 < UsecaseDef >2.4 < Usecase>2.5 < Targets>2.5.1 < Target>2.5.2 < Range>2.6 < Pipeline>2.…...

使用C++11实现Golang的defer功能
本文主要用C11标准来实现Golang的defer功能。 背景 目前笔者的主力语言是Golang,其次是C,再次是JS、Delphi。在Golang工程中大量使用了defer关键字实现函数的延迟调用。如打开文件的出错处理。近来在C工程中遇到类似需求,在函数返回时进行某…...
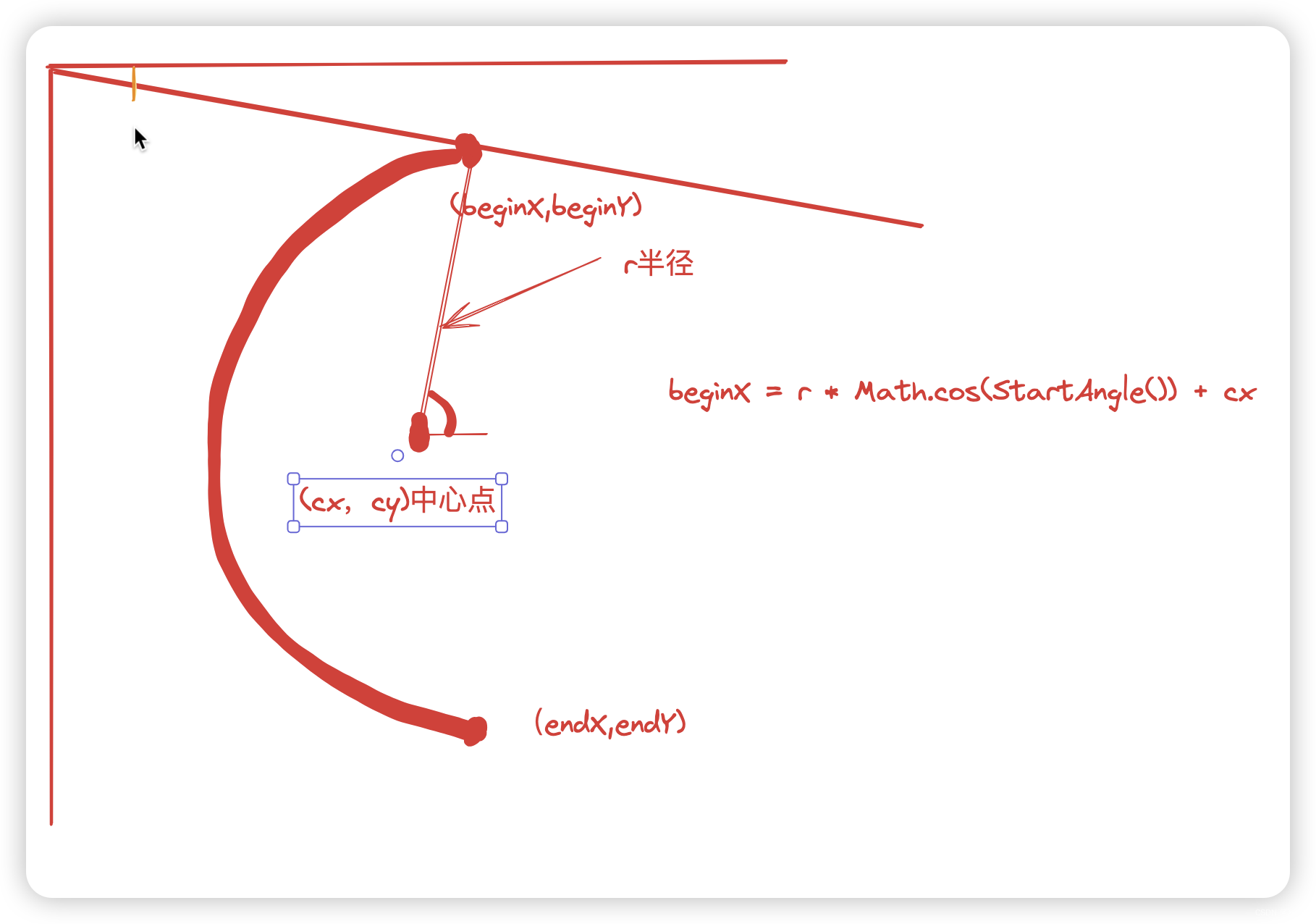
前端之电力系统SVG图低代码
其实所有的图形都是由点,线,面组成的。点线面可以组成一个设备。下面就简单讲讲点线面是怎么画的吧 对于线,可以用path <g><path:d"M ${beginX},${beginY} L ${endX},${endY}":stroke-width"lineWidth":strok…...

括号生成[中等]
优质博文:IT-BLOG-CN 一、题目 数字n代表生成括号的对数,请你设计一个函数,用于能够生成所有可能的并且 有效的 括号组合。 示例 1: 输入:n 3 输出:["((()))","(()())","(())(…...

配置ubuntu的VNC时遇到报错_XSERVTransmkdir: Mode of /tmp/.X11-unix should be set to 1777
现在win11内嵌了ubuntu系统,我在根据打造基于 VNC 的 Ubuntu 20.04 的远程桌面 配置VNC server时,到了 vncserver :1 这一步,遇到报错: vncserver: /usr/bin/Xtigervnc did not start up, please look into /root/.vnc/xxxxx.:1.…...
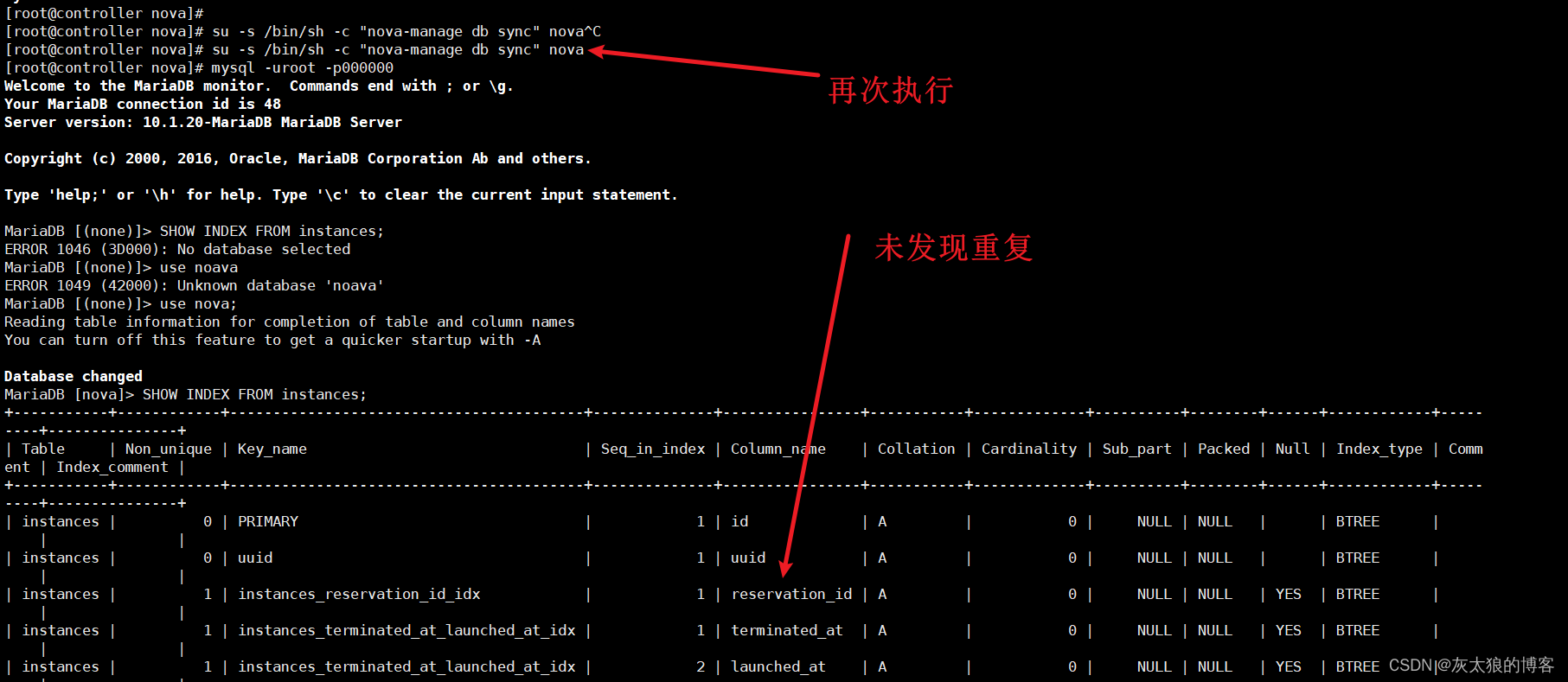
openstack部署nova中出现的问题:
[rootcontroller nova]# su -s /bin/sh -c “nova-manage db sync” nova /usr/lib/python2.7/site-packages/pymysql/cursors.py:170: Warning: (1831, u’Duplicate index block_device_mapping_instance_uuid_virtual_name_device_name_idx. This is deprecated and will be…...

【OpenCV 基础知识 3】边缘检测
文章目录 cvCanny完整示例代码 cvCanny 这行代码使用OpenCV库中的 cvCanny 函数对灰度图像进行边缘检测。让我解释一下: cvCanny(gray, dst, 10, 100, 3);gray: 这是输入的灰度图像,即要进行边缘检测的图像。dst: 这是输出的边缘图像,即将结…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...

springboot整合VUE之在线教育管理系统简介
可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生,小白用户,想学习知识的 有点基础,想要通过项…...

Java数值运算常见陷阱与规避方法
整数除法中的舍入问题 问题现象 当开发者预期进行浮点除法却误用整数除法时,会出现小数部分被截断的情况。典型错误模式如下: void process(int value) {double half = value / 2; // 整数除法导致截断// 使用half变量 }此时...
