括号生成[中等]
优质博文:IT-BLOG-CN

一、题目
数字n代表生成括号的对数,请你设计一个函数,用于能够生成所有可能的并且 有效的 括号组合。
示例 1:
输入:n = 3
输出:["((()))","(()())","(())()","()(())","()()()"]
示例 2:
输入:n = 1
输出:["()"]
1 <= n <= 8
二、代码
【1】暴力法: 我们可以生成所有2^2n个(和)字符构成的序列,然后我们检查每一个是否有效即可。为了生成所有序列,我们可以使用递归。长度为n的序列就是在长度为n−1的序列前加一个(或)。为了检查序列是否有效,我们遍历这个序列,并使用一个变量balance表示左括号的数量减去右括号的数量。如果在遍历过程中balance的值小于零,或者结束时balance的值不为零,那么该序列就是无效的,否则它是有效的。
class Solution {public List<String> generateParenthesis(int n) {List<String> combinations = new ArrayList<String>();generateAll(new char[2 * n], 0, combinations);return combinations;}public void generateAll(char[] current, int pos, List<String> result) {if (pos == current.length) {if (valid(current)) {result.add(new String(current));}} else {current[pos] = '(';generateAll(current, pos + 1, result);current[pos] = ')';generateAll(current, pos + 1, result);}}public boolean valid(char[] current) {int balance = 0;for (char c: current) {if (c == '(') {++balance;} else {--balance;}if (balance < 0) {return false;}}return balance == 0;}
}
时间复杂度: O(2^2n * n),对于2^2n个序列中的每一个,我们用于建立和验证该序列的复杂度为O(n)。
空间复杂度: O(n),除了答案数组之外,我们所需要的空间取决于递归栈的深度,每一层递归函数需要O(1)的空间,最多递归2n层,因此空间复杂度为O(n)。
【2】回溯法: 方法一还有改进的余地:我们可以只在序列仍然保持有效时才添加(或),而不是像 方法一 那样每次添加。我们可以通过跟踪到目前为止放置的左括号和右括号的数目来做到这一点,如果左括号数量不大于n,我们可以放一个左括号。如果右括号数量小于左括号的数量,我们可以放一个右括号。
class Solution {public List<String> generateParenthesis(int n) {List<String> ans = new ArrayList<String>();backtrack(ans, new StringBuilder(), 0, 0, n);return ans;}public void backtrack(List<String> ans, StringBuilder cur, int open, int close, int max) {if (cur.length() == max * 2) {ans.add(cur.toString());return;}if (open < max) {cur.append('(');backtrack(ans, cur, open + 1, close, max);cur.deleteCharAt(cur.length() - 1);}if (close < open) {cur.append(')');backtrack(ans, cur, open, close + 1, max);cur.deleteCharAt(cur.length() - 1);}}
}
我们的复杂度分析依赖于理解generateParenthesis(n)中有多少个元素。这个分析超出了本文的范畴,但事实证明这是第n个卡特兰数1/(n+1)(2n/n),这是由4n/n渐近界定的。
时间复杂度: O(4n/n),在回溯过程中,每个答案需要O(n)的时间复制到答案数组中。
空间复杂度: O(n),除了答案数组之外,我们所需要的空间取决于递归栈的深度,每一层递归函数需要O(1)的空间,最多递归2n层,因此空间复杂度为O(n)。
【3】按括号序列的长度递归: 任何一个括号序列都一定是由(开头,并且第一个(一定有一个唯一与之对应的)。这样一来,每一个括号序列可以用(a)b来表示,其中a与b分别是一个合法的括号序列(可以为空)。那么,要生成所有长度为2n的括号序列,我们定义一个函数generate(n)来返回所有可能的括号序列。那么在函数generate(n)的过程中:
1、我们需要枚举与第一个(对应的)的位置2i+1;
2、递归调用generate(i)即可计算a的所有可能性;
3、递归调用generate(n−i−1)即可计算b的所有可能性;
4、遍历a与b的所有可能性并拼接,即可得到所有长度为2n的括号序列。
为了节省计算时间,我们在每次generate(i)函数返回之前,把返回值存储起来,下次再调用generate(i)时可以直接返回,不需要再递归计算。
class Solution {ArrayList[] cache = new ArrayList[100];public List<String> generate(int n) {if (cache[n] != null) {return cache[n];}ArrayList<String> ans = new ArrayList<String>();if (n == 0) {ans.add("");} else {for (int c = 0; c < n; ++c) {for (String left: generate(c)) {for (String right: generate(n - 1 - c)) {ans.add("(" + left + ")" + right);}}}}cache[n] = ans;return ans;}public List<String> generateParenthesis(int n) {return generate(n);}
}
时间复杂度: O(4^n/n),该分析与方法二类似。
空间复杂度: O(4^n/n),此方法除答案数组外,中间过程中会存储与答案数组同样数量级的临时数组,是我们所需要的空间复杂度。
相关文章:

括号生成[中等]
优质博文:IT-BLOG-CN 一、题目 数字n代表生成括号的对数,请你设计一个函数,用于能够生成所有可能的并且 有效的 括号组合。 示例 1: 输入:n 3 输出:["((()))","(()())","(())(…...

配置ubuntu的VNC时遇到报错_XSERVTransmkdir: Mode of /tmp/.X11-unix should be set to 1777
现在win11内嵌了ubuntu系统,我在根据打造基于 VNC 的 Ubuntu 20.04 的远程桌面 配置VNC server时,到了 vncserver :1 这一步,遇到报错: vncserver: /usr/bin/Xtigervnc did not start up, please look into /root/.vnc/xxxxx.:1.…...
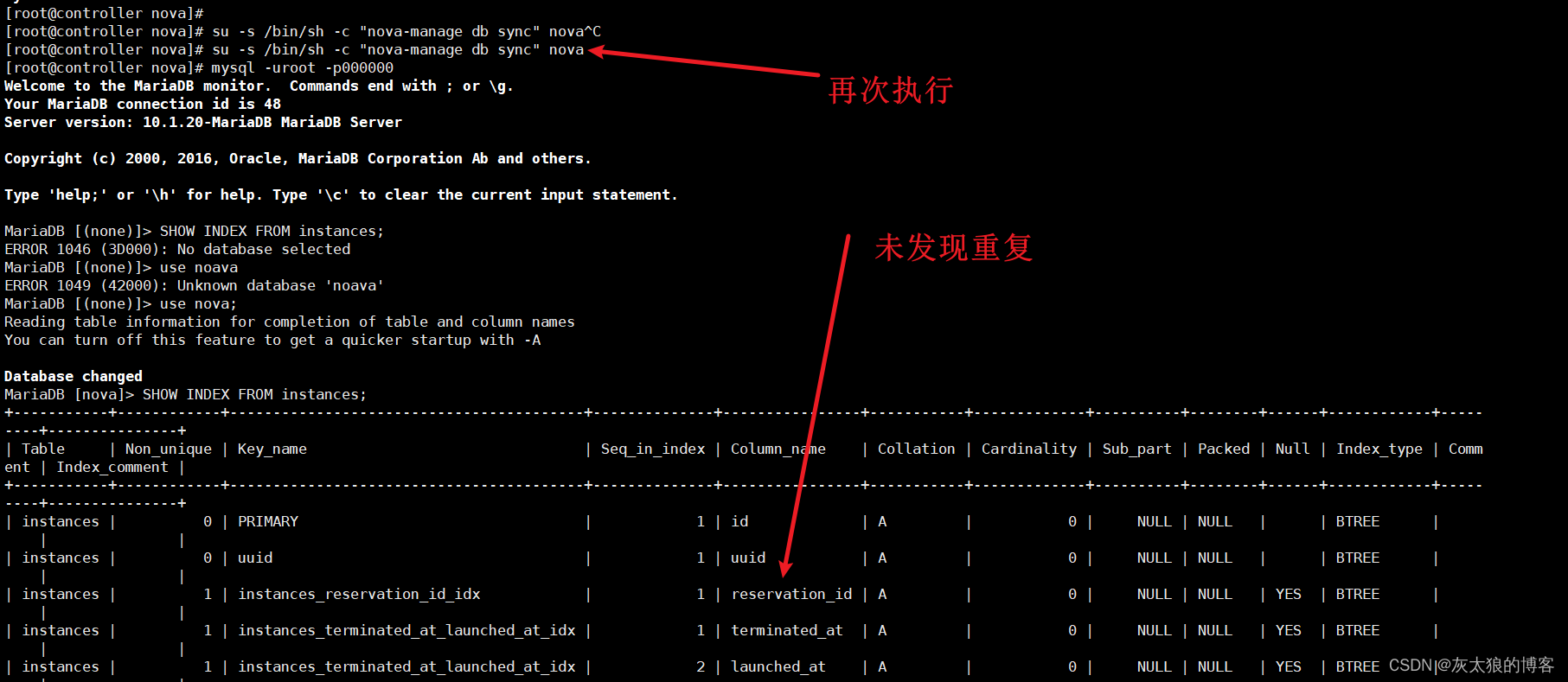
openstack部署nova中出现的问题:
[rootcontroller nova]# su -s /bin/sh -c “nova-manage db sync” nova /usr/lib/python2.7/site-packages/pymysql/cursors.py:170: Warning: (1831, u’Duplicate index block_device_mapping_instance_uuid_virtual_name_device_name_idx. This is deprecated and will be…...

【OpenCV 基础知识 3】边缘检测
文章目录 cvCanny完整示例代码 cvCanny 这行代码使用OpenCV库中的 cvCanny 函数对灰度图像进行边缘检测。让我解释一下: cvCanny(gray, dst, 10, 100, 3);gray: 这是输入的灰度图像,即要进行边缘检测的图像。dst: 这是输出的边缘图像,即将结…...
)
拓宽知识储备量(指数级成长)
对于增强自己的知识储备,不是什么知识都往脑袋里去塞,最好的办法就是让自己的心态回到自己初心的时候,始终保值一颗学者的心,你像那些成功人士,比如格力,华为,腾讯等这样的大公司创始人哪个不是…...

x264 帧类型代价计算原理:slicetype_mb_cost 函数分析
slicetype_mb_cost 函数 函数功能 计算每个宏块 MB 的代价 cost。函数参数分析 x264_t *h:全局编码结构体x264_mb_analysis_t *a:宏块分析结构体x264_frame_t **frames:系列帧数据结构体int p0:帧序号之一,一般指向靠前帧int p1:帧序号之一,一般指向靠后帧int b:帧标志…...
战网国际服加速器哪个好用 暴雪战网免费加速器分享
战网国际服(Battle.net International或Battle.net Global)是由暴雪娱乐公司(Blizzard Entertainment)运营的面向全球玩家的多人在线游戏平台。与专注于特定地区的版本不同,国际服允许玩家不受地域限制地访问暴雪的多款…...
Java入门基础学习笔记26——break,continue
跳转关键字: break: 跳出并结束当前所在循环的执行。 continue: 用于跳出当前循环中的当次执行,直接进入循环中的下一次执行。 package cn.ensource.loop;public class BreakContinueDemo8 {public static void main(String[] a…...

HNU-算法设计与分析-作业6
第六次作业【分支限界法】 文章目录 第六次作业【分支限界法】<1> 算法实现题6-2 最小权顶点覆盖问题<2> 算法实现题6-6 n后问题<3> 算法实现题6-7 布线问题 <1> 算法实现题6-2 最小权顶点覆盖问题 ▲问题重述 问题描述: 给定一个赋权无向…...

2D Chests Assets - Mega Pack
科幻/奇幻/经典主题的箱子和容器。AAA质量,高分辨率,VFX,源PSD文件。 这是一个带有手绘套装的大包装: -【梦幻之栗】 -【科幻钱包】 AAA质量。高分辨率。一切都已准备就绪,可供使用。包括PSD文件。 在1.1版本中添加了VFX并将项目更新为URP。请注意,新的VFX仅适用于URP/HD…...
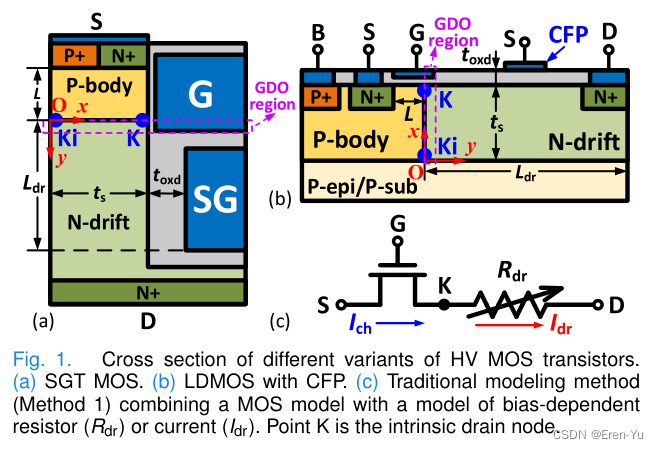
一种基于电场连续性的高压MOSFET紧凑模型,用于精确表征电容特性
来源:A Compact Model of High-Voltage MOSFET Based on Electric Field Continuity for Accurate Characterization of Capacitance(TED 24年) 摘要 本文提出了一种新的高压MOSFET(HV MOS)紧凑模型,以消…...

vue阶段性测试题,内容丰富,案例典型,题目配有答案
阶段性测试 理论题实践题 1)理论题 请简述Vue、Node.js、Vscode是什么,以及有什么关系 1. vue是一个轻量级、比较灵活的且支持组件开发的网络框架 2. node.js是让JavaScript运行在服务器上的一直环境 3. Vscode是一款有着丰富插件的代码编辑器 4. 关系…...
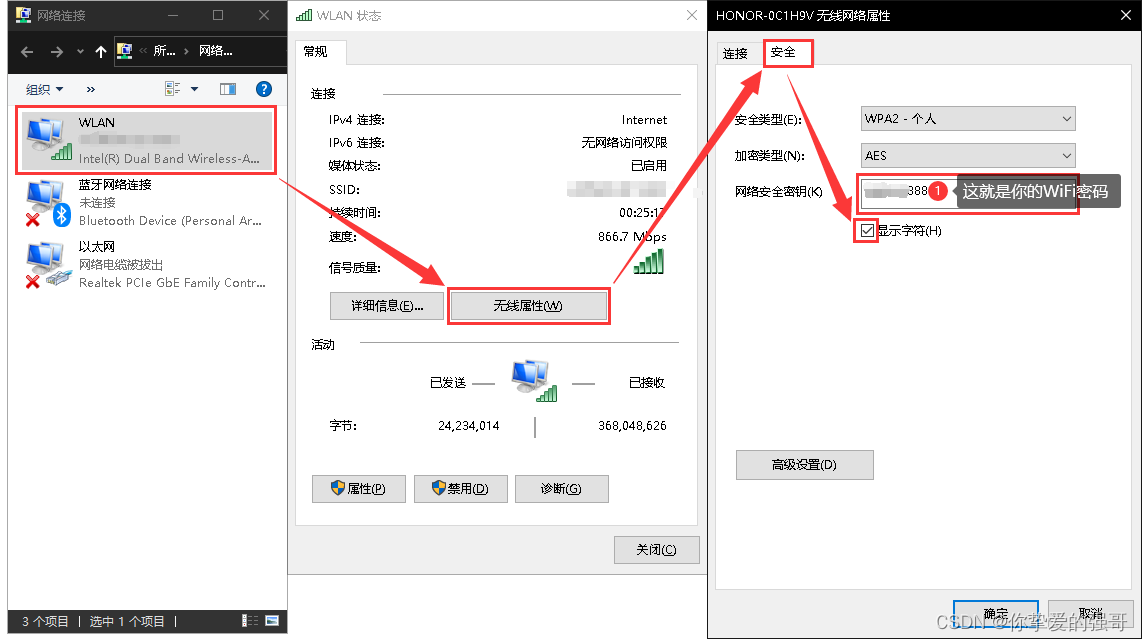
如何查看PC电脑已经已经连接上的网络WiFi密码?
运行ncpa.cpl...

Java 语言的特点分析及应用
Java语言自问世以来,因其独特的设计理念和广泛的应用领域,成为了编程语言中的一颗璀璨明星。以下是对Java语言特点的详细分析及其实际应用场景,希望能帮助面试者更好地理解和掌握Java的优势。 1. 简单易学 Java的语法简单,类似于…...
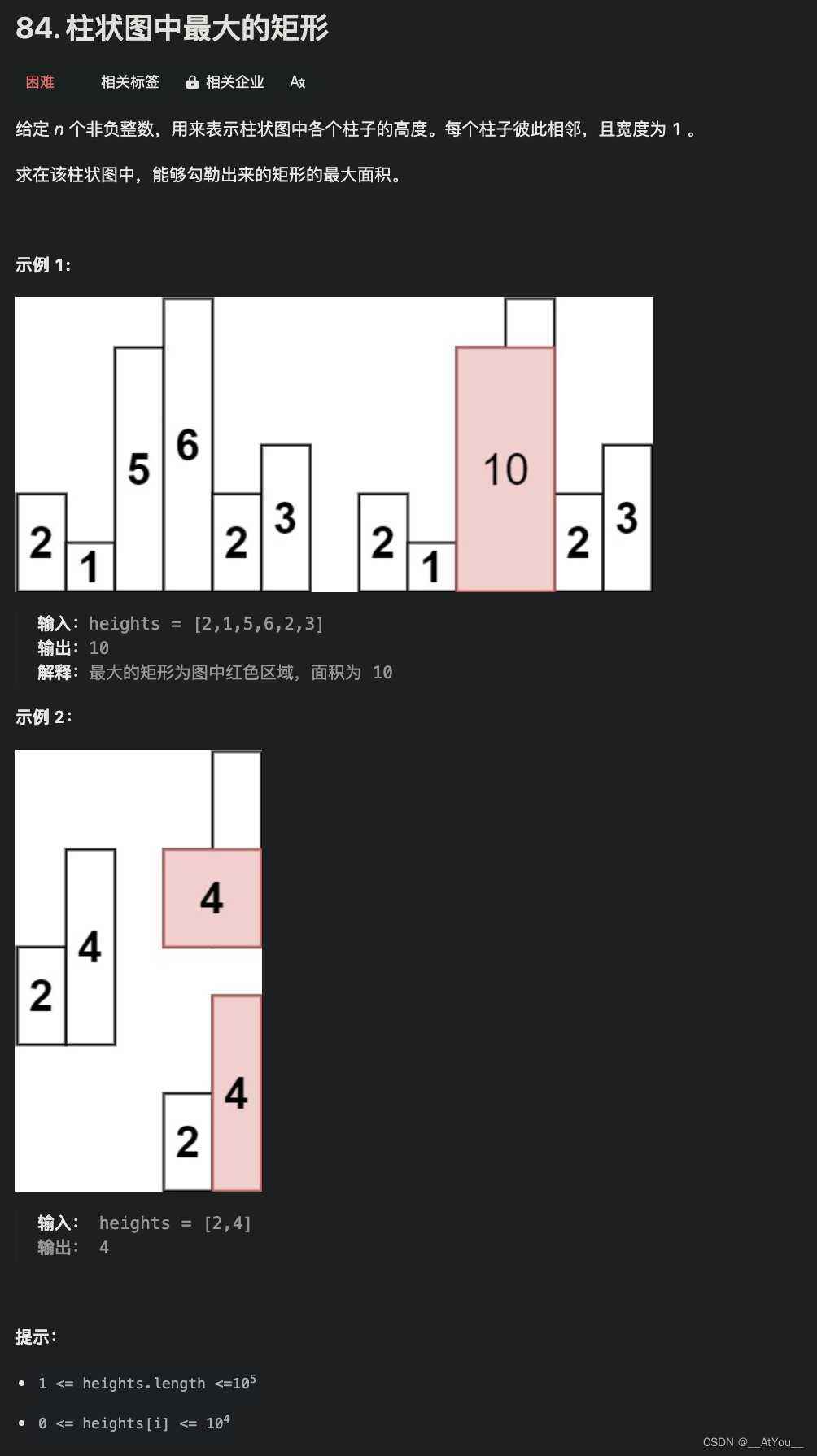
Golang | Leetcode Golang题解之第84题柱状图中最大的矩形
题目: 题解: func largestRectangleArea(heights []int) int {n : len(heights)left, right : make([]int, n), make([]int, n)for i : 0; i < n; i {right[i] n}mono_stack : []int{}for i : 0; i < n; i {for len(mono_stack) > 0 &&am…...
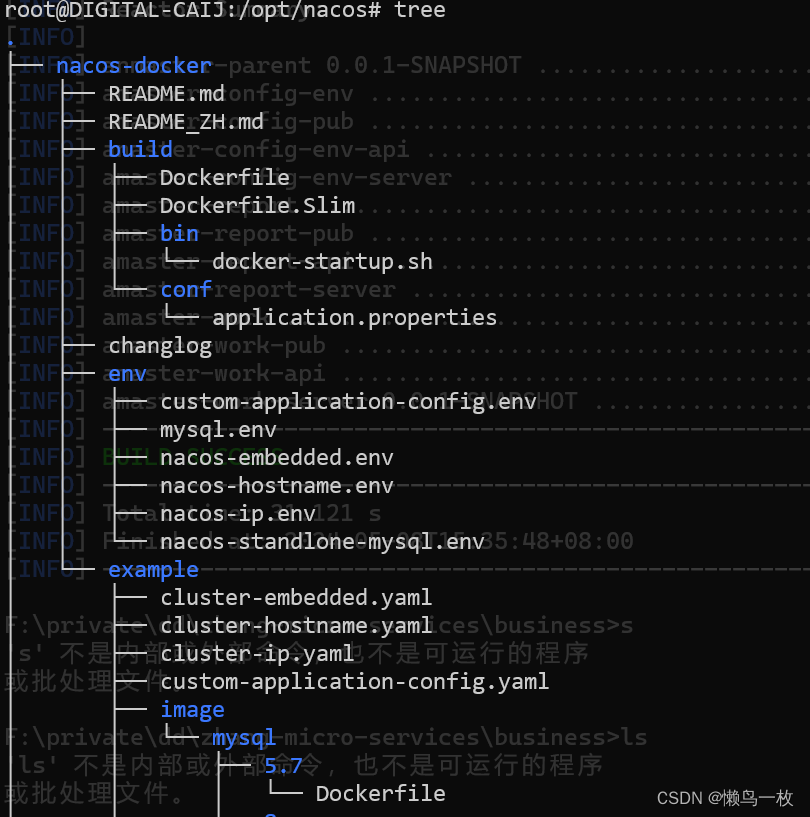
linux实用命令
一、常用命令 mkdir -p mkdir -p 命令用于在Unix和Linux系统中创建目录。其中,-p参数确保目录名称存在,如果目录不存在的就新创建一个。换句话说,-p参数允许创建一个目录和它不存在的父目录,确保了指定的整个目录路径都会被…...

创建和管理数据库
1. 一条数据的存储过程 存储数据是处理数据的第一步.只有正确的把数据存储起来,我们才能进行有效的处理和分析.否则,只能是一团乱麻.在MySQL中,一个完整的数据存储过程一共有四步 : 创建数据库,确认字段,创建数据表&a…...

Spring STOMP-发送消息
如果你想要从应用程序的任何地方向连接的客户端发送消息,要怎么做?任何应用程序组件都可以向brokerChannel发送消息。要这样做,最简单方法是注入一个SimpMessagingTemplate并使用它来发送消息。通常,你会按类型注入它,…...

kubernetes多master集群架构
一、完成master02节点的初始化操作 master02环境准备,详细过程参考上一期博客环境准备 #添加主机映射 vim /etc/hosts 192.168.88.3 master01 192.168.88.8 master02 192.168.88.4 node01 192.168.88.5 node021、准备master02节点需要的文件 从 master01 节点上拷…...
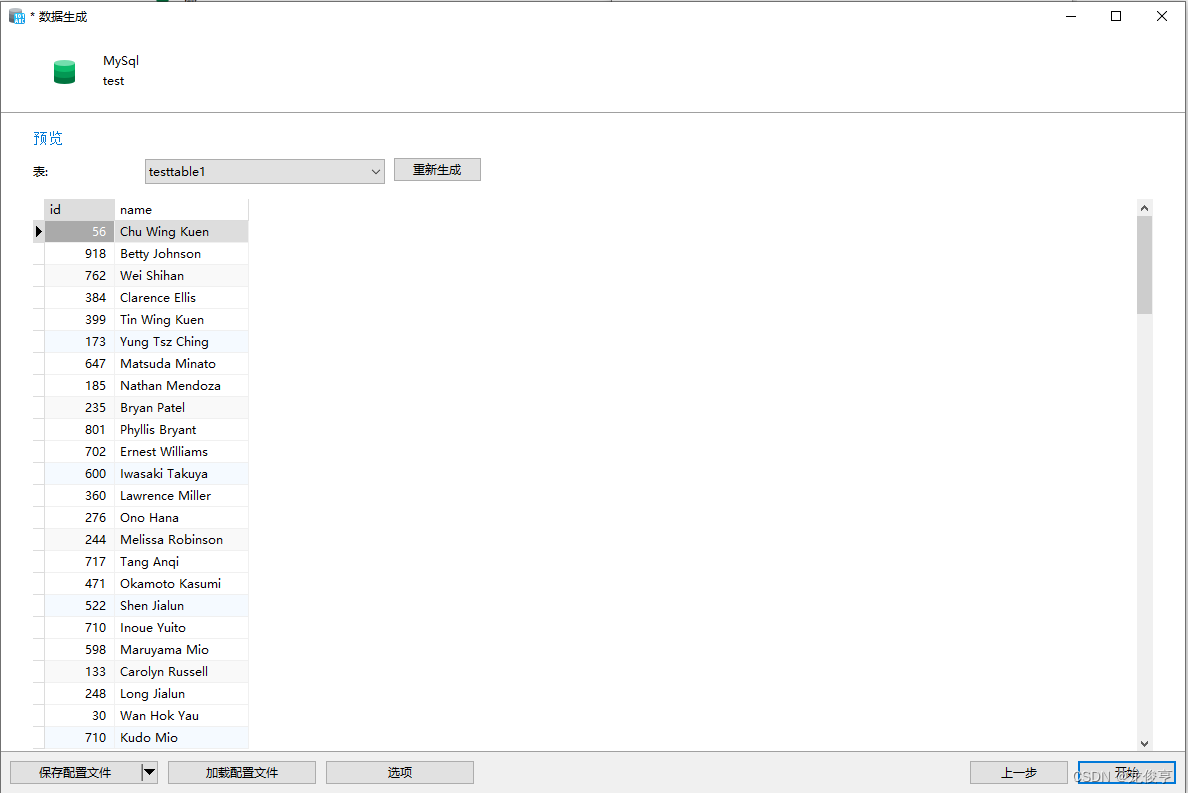
MySQL数据库的初始化(创建库、创建表、向数据库添加测试数据)
MySQL数据库的初始化(创建库、创建表、修改数据库访问密码、向数据库添加测试数据) MySQL数据库简介MySQL创建一个新的数据库修改数据库访问密码 MySQL创建一张新的数据表简单(设置)表复杂(设置)表 填充测试…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...
