2024CCPC郑州邀请赛暨河南省赛
比赛记录:看群里大家嘎嘎拿牌,自己个人来solo了一下,发现简单到中等题很多,写了两小时出了7题,但是写的比较慢,对难题把握还是不准确
![]()
补题 : A题确实巧妙充分利用题目的数据范围来思考问题,D简单数数性质推理
A.Once In My Life
数理逻辑推理
题目要求我们构造奇怪的式子得满足出现123456789 + 一个指定的数,给定n要求找到一个k使得n*k符合要求,同时告诉我们 n < 1e8,k<2e10,可以注意到两者的乘积是刚好到达上限1e18级别那么我们如何去思考:我们无非就是想找到一个符合要求的数(1e18)同时是n的倍数->推出k,依照数据范围我们应该是在时间求出答案,我们看如何得到这个数,可以看到1234567890 + d是10位数 后面还可以接上8位数,也就是说这个 + 与n同级别数是可以构造出来的,那么构造完成之后加上快要变成n倍数的余数就是n的倍数了
void solve(){LL n,d; cin>>n>>d;LL ans = 1234567890 + d;LL x=n;while(x){x/=10;ans *= 10;}ans += (n-ans%n)%n;cout << ans/n << endl;return ;
}B.扫雷1
贪心
我们是从前往后走的,可以得到如果要选择当前这个数必然是因为后面的点都小于等于这个数,否则我直接买后面的更优,所以我们只需要预处理出来后缀最小值即可
int w[N],suf[N];
void solve(){cin>>n;for(int i=1;i<=n;i++) cin>>w[i];suf[n+1]=2e9;for(int i=n;i>=1;i--) suf[i]=min(suf[i+1],w[i]);int ans=0,cnt=0;for(int i=1;i<=n;i++){ans++;if(ans>=w[i]){if(w[i]<=suf[i+1]){cnt += ans/w[i];ans %= w[i];}}}cout << cnt << endl;return ;
}D.距离之比
数学推理
我们可以对题目中式子进行推理之后就是两个点之间的横纵坐标构成的三角形的的三角函数之比
我们对这个式子研究单调性之后可以得出结论实在45度或者135度的时候结果是最优的所以我们分别按照 x + y 和 x - y排序之后求解相邻两个点的结果即可
PII e[N];
bool cmp1(PII a,PII b){return a.x+a.y<b.x+b.y;
}
bool cmp2(PII a,PII b){return a.x-a.y<b.x-b.y;
}double get(PII a,PII b){double dx = abs(a.x-b.x),dy = abs(a.y - b.y);return 1.0*(dx+dy)/sqrtl((dx*dx+dy*dy));
}
void solve(){cin>>n;for(int i=1;i<=n;i++){int x,y; cin>>x>>y;e[i]={x,y};} sort(e+1,e+1+n,cmp1);double ans = 0;for(int i=1;i<=n;i++){int last = i==1 ? n : i-1;double now =get(e[i],e[last]);ans = max(ans,now);}sort(e+1,e+1+n,cmp2);for(int i=1;i<=n;i++){int last = i==1 ? n : i-1;double now =get(e[i],e[last]);ans = max(ans,now);}cout << LF(11) << ans << endl;return ;
}F.优秀字符串
签到模拟
直接按照题目意思要操作即可
void solve(){cin>>n;int ans = 0;while(n--){string s; cin>>s; if(s.size()!=5) continue;s=' '+s;set<char> S;for(int i=1;i<=4;i++) S.insert(s[i]);if(S.size()!=4) continue;if(s[3]!=s[5]) continue;ans ++ ;}cout << ans << endl;return ;
}H.随机栈
模拟+概率
要求我们得到的是递增的序列,那么我们取出来的数一定是当前集合最小的数才有可能,同时取出来的数的概率为 ,用快速幂求逆元,维护集合最小值可以用优先队列,数量开个桶即可
LL qmi(LL a,LL b,LL p){LL res = 1;while(b){if(b&1) res=res*a%p;b>>=1;a=a*a%p;}return res;
}LL inv(LL x){return qmi(x,mod-2,mod);
}void solve(){cin>>n;priority_queue<int,vector<int>,greater<int>> q;vector<int> cnt(N);LL ans = 1;for(int i=1;i<=2*n;i++){int x; cin>>x;if(x!=-1) q.push(x),cnt[x]++;else{int x = q.top();ans *= (LL)cnt[x]*qmi((int)q.size(),mod-2,mod)%mod;ans %= mod;ans = (ans+mod)%mod;a.push_back(x); q.pop();cnt[x]--;}}int last = -1;bool ok = true;for(auto&v:a){if(v>=last) last=v;else{ok = false; break;}}if(!ok){cout << 0 << endl;return ;}ans = (ans%mod+mod)%mod;cout << ans << endl;return ;
}J.排列和组合
暴力 or 小推理
做法1:我们可以发现测试数据不多,我们可以直接跑出全排列即可,可以用素数筛跑出来当前这个数是不是合数
做法2:以0,2,4,5,6,8结尾的一定是合数,由于歌巢原理这六个数至少会出现一个,调整到最后位置即可
int p[N];
bool st[N];
int cnt;
void get(){for(int i=2;i<N;i++){if(!st[i]) p[cnt++]=i;for(int j=0;p[j]<N/i;j++){st[i*p[j]]=true;if(i%p[j]==0) break;}}
}
void solve(){int n = 5;int x; cin>>x;for(int i=1;i<=n;i++) p[i]=x%10,x/=10;sort(p+1,p+1+n);do{int now = 0;for(int i=1;i<=n;i++) now = now*10+p[i];if(now<10000) continue;if(st[now]){cout << now << endl;return ;}}while(next_permutation(p+1,p+1+n));return ;
}K.树上问题
树形dp
我们首先把1当成根来处理可以发现每一次换根节点只会影响当前这一条边,做个简单树形dp转移即可
vector<int> g[N];
int dp[N];void dfs1(int u,int fa){dp[u]= (2*a[u]>=a[fa]);for(auto&v:g[u]){if(v==fa) continue;dfs1(v,u);dp[u] += dp[v];}
}
void dfs2(int u,int fa){if(u!=1) dp[u] = dp[fa] - (2*a[u]>=a[fa]) + (2*a[fa]>=a[u]);for(auto&v:g[u]){if(v==fa) continue;dfs2(v,u);}
}
void solve(){cin>>n;for(int i=1;i<=n;i++) g[i].clear(),dp[i]=0;for(int i=1;i<=n;i++) cin>>a[i];for(int i=1;i<n;i++){int a,b; cin>>a>>b;g[a].push_back(b);g[b].push_back(a);} dfs1(1,0);dfs2(1,0);int ans = 0;for(int i=1;i<=n;i++) ans += dp[i]==n;cout << ans << endl;return ;
}L.Toxel 与 PCPC II
dp处理
我们可以发现对于当前点一定就是从前面几个点转移过来的,也就是说从上一次的最优情况到当前我和前面那几个一起,我们发现由于很大,所以转移的次数不是很大简单论证一下就是n开四次方即可,我们可以处理到30,这样我们来定义dp[i][j]为当前处理到第i个数,处理第i个的时候是一次性处理j个以前debug的,时间复杂度就是30n
LL dp[N][32];
LL d[N];void solve(){cin>>n>>m;for(int i=1;i<=m;i++) cin>>a[i];for(int i=1;i<=m;i++){d[i]=2e18;for(int j=1;j<=i and j<=30;j++){dp[i][j]=d[i-j]+a[i]+(LL)j*j*j*j;d[i]=min(d[i],dp[i][j]);}}cout << d[m] << endl;return ;
}M.有效算法
二分
依照题目意思我们发现明显的具有二分性质,接下来思考如何check我们直接依照式子推导可以得到
对于每一个a,b可以得到一个区间,也就是所有的区间要有一个交点即可,也就是最大的右端点要小于最小的左端点
LL a[N],b[N];void solve(){cin>>n;for(int i=1;i<=n;i++) cin>>a[i];for(int i=1;i<=n;i++) cin>>b[i];auto check = [&](LL k){LL l=-2e18,r=2e18;for(int i=1;i<=n;i++){l=max(l,a[i]-k*b[i]);r=min(r,a[i]+k*b[i]);}return l<=r;};LL l = 0 ,r = 1e9;while(l<r){LL mid = l+r>>1;if(check(mid)) r=mid;else l=mid+1;}cout << l << endl;return ;
}相关文章:
2024CCPC郑州邀请赛暨河南省赛
比赛记录:看群里大家嘎嘎拿牌,自己个人来solo了一下,发现简单到中等题很多,写了两小时出了7题,但是写的比较慢,对难题把握还是不准确 补题 : A题确实巧妙充分利用题目的数据范围来思考问题&…...
Spring 各版本发布时间与区别
版本版本特性Spring Framework 1.01. 所有代码都在一个项目中 2. 支持核心功能IoC、AOP 3. 内置支持Hibernate、iBatis等第三方框架 4. 对第三方技术简单封装。如:JDBC、Mail、事务等 5. 只支持XML配置方式。6.主要通过 XML 配置文件来管理对象和依赖关系࿰…...

前端模块导入导出方式
不同的导出方式和相应的导入方式,可以提炼成 3 种类型:name、default 和 list。 以下是使用示例: // Name Export | Name Import // 一个“命名”的导出 export const name value import { name } from ...❌ 错误示例: export…...

docker01-简介和概述
什么是docker? 我们现在开发项目是在windows操作系统使用idea开发,本地windows操作系统上有我们项目所需的jdk,mysql,redis,tomcat等环境,如果我们想打包我们的项目到一个别的服务器上,在别的服…...
)
java数据结构与算法(对称二叉树)
前言 为什么学习数据结构和算法? 1.直面大厂的高薪。 2.学习编程的语言。 3.输出优雅的代码和高性能的程序。 每日练习2题,希望大家都能收获高薪offer,实现自由跳槽。 实现原理 主要判断二叉树的以中间线为轴,两边的对称的…...
现代C++的std::function, 强大的多态函数包装器(包含std::mem_fn使用方式).)
[原创](Modern C++)现代C++的std::function, 强大的多态函数包装器(包含std::mem_fn使用方式).
[简介] 常用网名: 猪头三 出生日期: 1981.XX.XX QQ联系: 643439947 个人网站: 80x86汇编小站 https://www.x86asm.org 编程生涯: 2001年~至今[共22年] 职业生涯: 20年 开发语言: C/C、80x86ASM、PHP、Perl、Objective-C、Object Pascal、C#、Python 开发工具: Visual Studio、D…...

解决间歇性 SSLPeerUnverifiedException 问题
问题背景 您在使用 SonarQube 与 GitHub Enterprise 进行拉取请求装饰时,遇到了间歇性的 javax.net.ssl.SSLPeerUnverifiedException 异常。具体错误信息如下: txt javax.net.ssl.SSLPeerUnverifiedException: Hostname XXXXXXX not verified (no certificates)at okhttp3…...

Linux程序开发(一):Linux基础入门安装和实操手册
Tips:"分享是快乐的源泉💧,在我的博客里,不仅有知识的海洋🌊,还有满满的正能量加持💪,快来和我一起分享这份快乐吧😊! 喜欢我的博客的话,记得…...
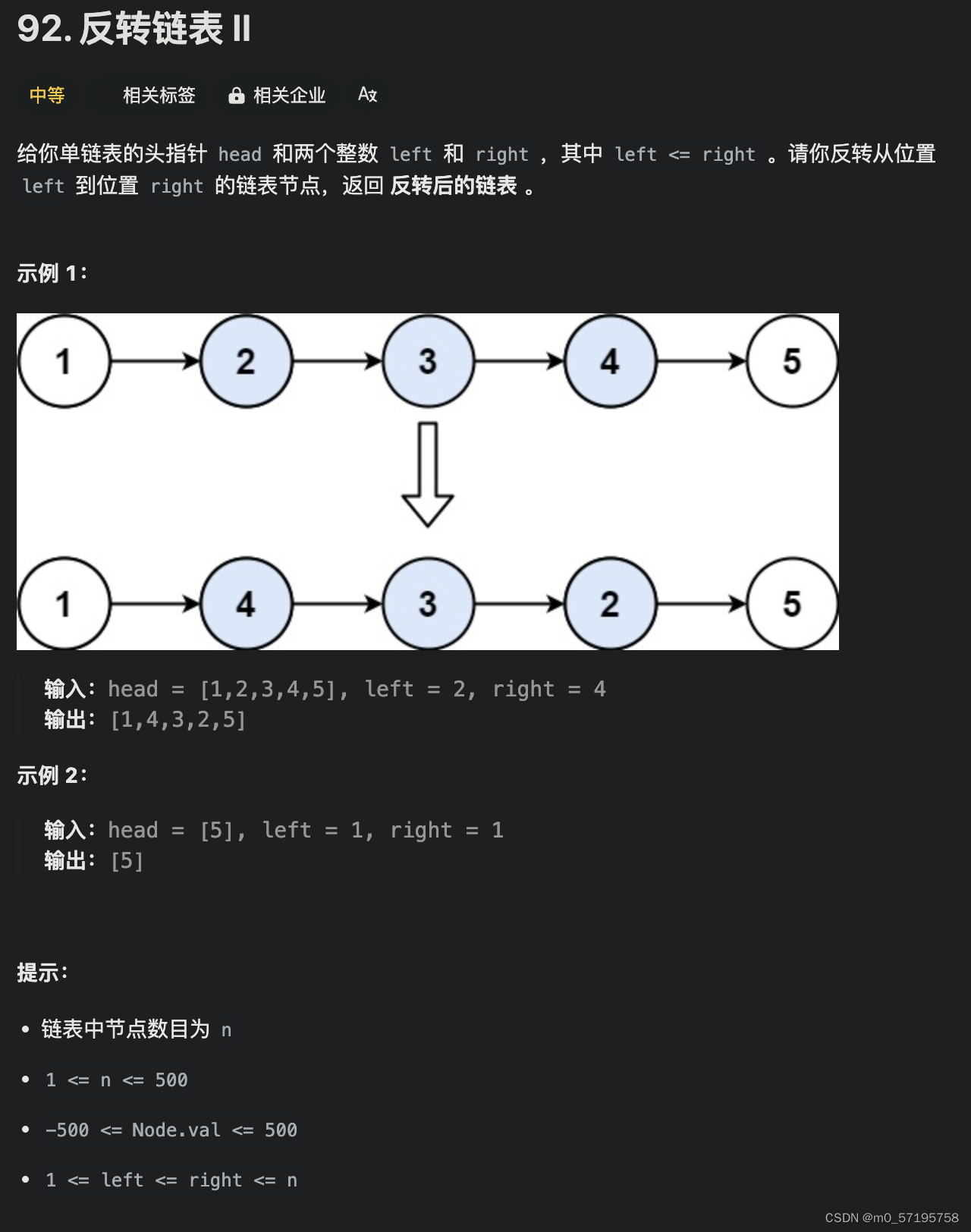
Java | Leetcode Java题解之第92题反转链表II
题目: 题解: class Solution {public ListNode reverseBetween(ListNode head, int left, int right) {// 设置 dummyNode 是这一类问题的一般做法ListNode dummyNode new ListNode(-1);dummyNode.next head;ListNode pre dummyNode;for (int i 0; …...
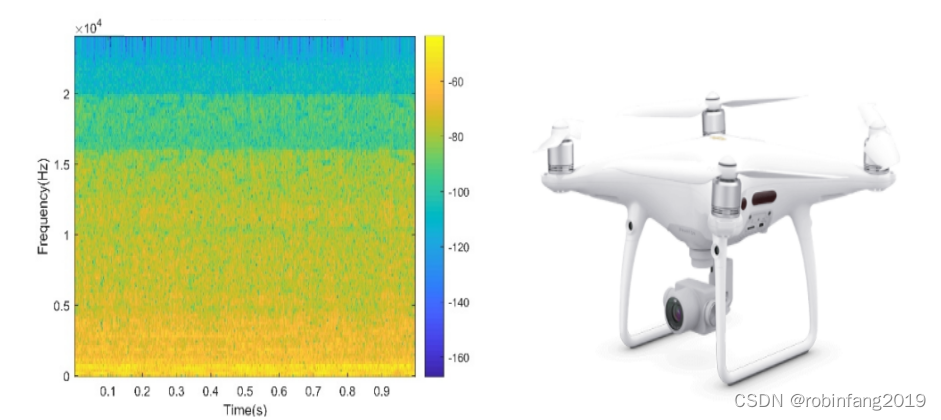
声纹识别在无人机探测上的应用
无人机在民用和军事领域的应用越来越广泛。然而,随着无人机数量的增加,"黑飞"现象也日益严重,对公共安全和隐私构成了威胁。因此,开发有效的无人机探测与识别技术变得尤为重要。及时发现黑飞无人机的存在进而对其型号进…...

【数据结构】时间、空间复杂度实例分析
跌倒了,就重新站起来,继续向前走;傻坐在地上是没用的。💓💓💓 目录 •✨说在前面 🍋知识点一:算法的效率 • 🌰1.斐波那契数列的第n项 • 🌰2.算法的复杂度…...

2024生日快乐祝福HTML源码
源码介绍 2024生日快乐祝福HTML源码,源码由HTMLCSSJS组成,记事本打开源码文件可以进行内容文字之类的修改,双击html文件可以本地运行效果,也可以上传到服务器里面, 源码截图 源码下载 2024生日快乐祝福HTML源码...
Android系统不同版本存储权限
一、Android存储简介 Android系统分为内部存储和外部存储 从Android6.0开始不断在更新存储(读写)权限,除了在AndroidManifest.xml文件里声明,app运行时也要动态申请使用对应的权限 提醒:应用私有存储不需要动态申请权…...

ue引擎游戏开发笔记(41)——行为树的建立(2)--丰富ai行为:巡逻后返回原处
1.需求分析: 就敌人ai而言,追踪到敌人有可能丢失目标,丢失目标后应该能返回原来位置,实现这一功能。 2.操作实现: 1.思路:利用clear value函数,禁用掉当前的追踪功能,执行之后的返…...
)
Linux quotacheck命令教程:如何检查和修复文件系统的磁盘配额(附案例详解和注意事项)
Linux quotacheck命令介绍 quotacheck命令是用于扫描文件系统以检查磁盘配额的一致性。它生成、检查和修复配额文件。这个命令通常在系统引导时运行,或者在手动更改了配额设置后运行。 Linux quotacheck命令适用的Linux版本 quotacheck命令在大多数Linux发行版中…...

Response对象的学习
Response对象在Web开发中是一个重要的概念,它代表了服务器对客户端请求的响应。当客户端(如浏览器)向服务器发送一个请求后,服务器会生成一个Response对象,其中包含了服务器返回给客户端的数据、状态码、响应头等信息。…...
QCustomplot---动态图
QCustomplot绘制动态曲线图-游标及鼠标跟踪显示数值_qcustomplot 游标-CSDN博客 m_timer new QTimer(this);connect(m_timer,SIGNAL(timeout()),this,SLOT(slotTimeout()));m_timer->start(50); void MainWindow::slotTimeout() {static int p0;static int i0;double m,m1…...
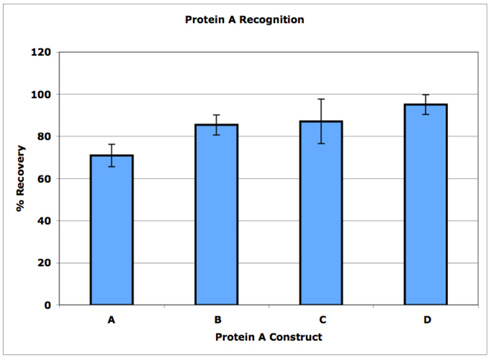
蛋白聚乙二醇化修饰检测试剂盒
蛋白多肽因其高生物活性、高特异性等优点备受药物开发商和研究者的青睐。但分子量大、亲水性强、稳定性差等劣势限制了蛋白多肽在临床上的应用,特别是蛋白多肽作为一种异源蛋白具有很强的免疫原性,容易被机体免疫系统识别并清除,导致药物的血…...
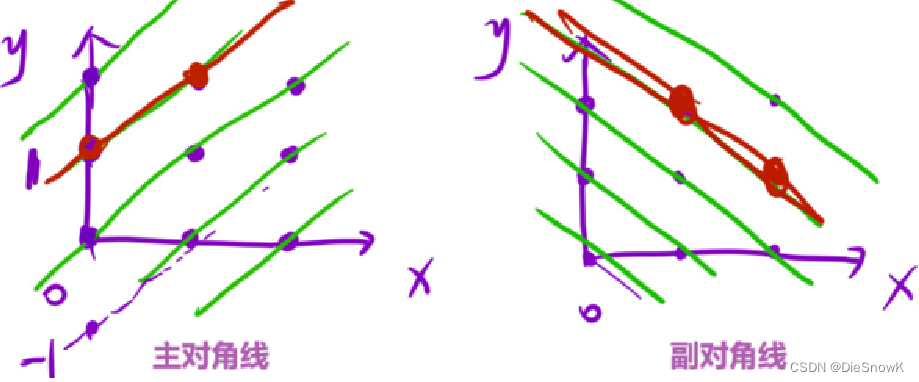
[Algorithm][回溯][字母大小写全排列][优美的排列][N皇后]详细讲解
目录 1.字母大小写全排列1.题目链接2.算法原理详解3.代码实现 2.优美的排列1.题目链接2.算法原理详解3.代码实现 3.N 皇后1.题目链接2.算法原理详解3.代码实现 1.字母大小写全排列 1.题目链接 字母大小写全排列 2.算法原理详解 本题逻辑与子集大致相同 思路一:每…...

.NET_NLog
步骤 1. 添加依赖 ①Microsoft.Extensions.DependencyInjection ②NLog.Extensions.Logging(或Microsoft.Extensions.Logging.___) Tutorial NLog/NLog Wiki GitHub 2.添加nlog.config文件(默认名称, 可改为其他名称, 但需要另行配置) 文件的基础…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

R 语言科研绘图第 55 期 --- 网络图-聚类
在发表科研论文的过程中,科研绘图是必不可少的,一张好看的图形会是文章很大的加分项。 为了便于使用,本系列文章介绍的所有绘图都已收录到了 sciRplot 项目中,获取方式: R 语言科研绘图模板 --- sciRplothttps://mp.…...
