MATLAB车辆动力学建模 ——《控制系统现代开发技术》
引言
在上这门课之前,我已经用过CasADi 去做过最优化的相关实践,其中每一步迭代主要就是由:对象系统+优化求解两部分组成的。这里我们重点介绍 “对象系统”如何去描述 ,因为它是每一步迭代中重要的一环——“优化求解”会获得控制输入u,u需要作用于模型,获得状态,以去计算目标函数“代价”。在上该课之前,我并没有系统的认识,因此,这门课让我对自己之前的实践有了全新的认识。
致谢
感谢BIT的智能车辆研究所的于会龙老师,其事无巨细的教导,手把手教学让身为研究牲的我感慨万分。
前言
虽然标题是车辆动力学, 但例子是车子的垂向减震系统哈。抱歉
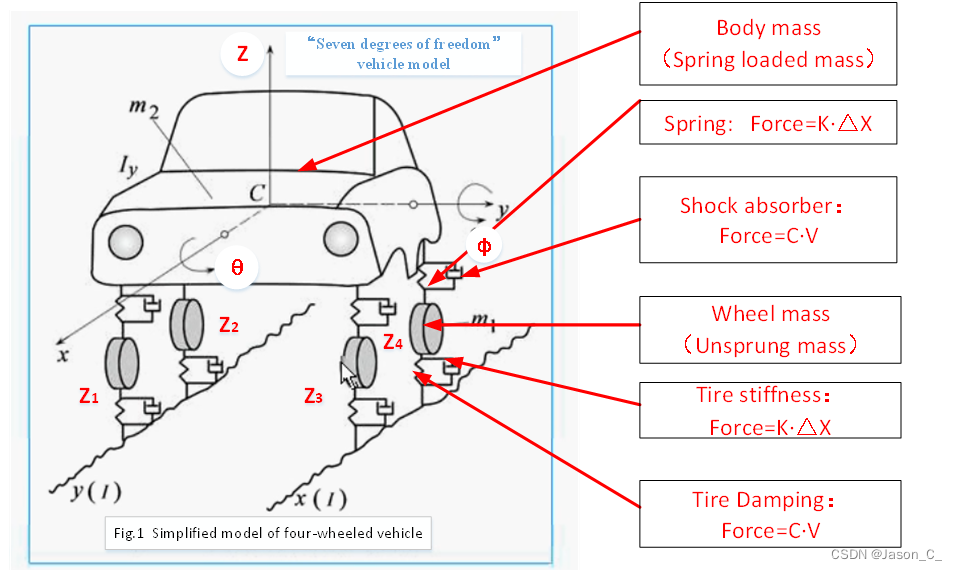
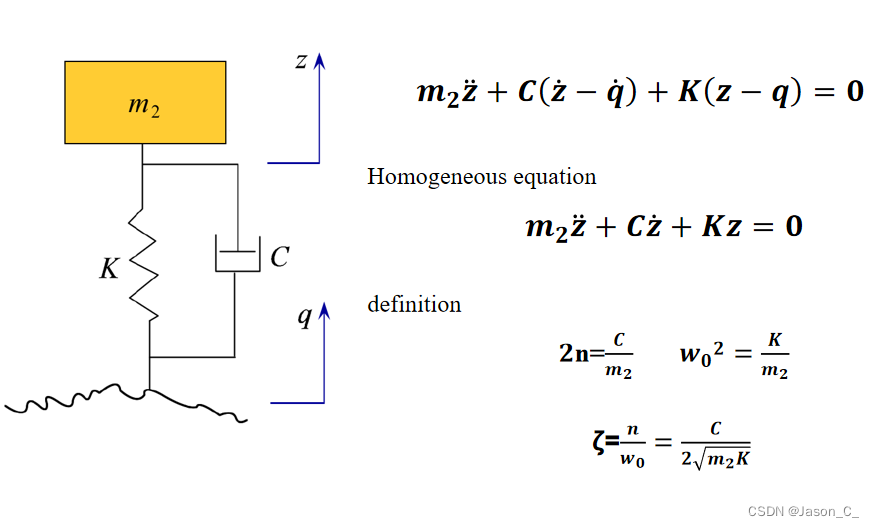
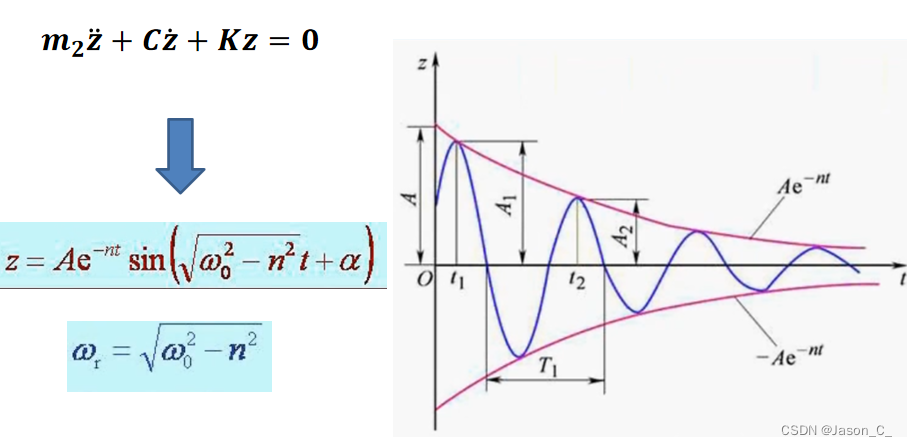
代码流程
这个流程很重要,大家仔细体会。6)-10)步就不放图了,大家直接在后面的代码里寻找对应的部分。
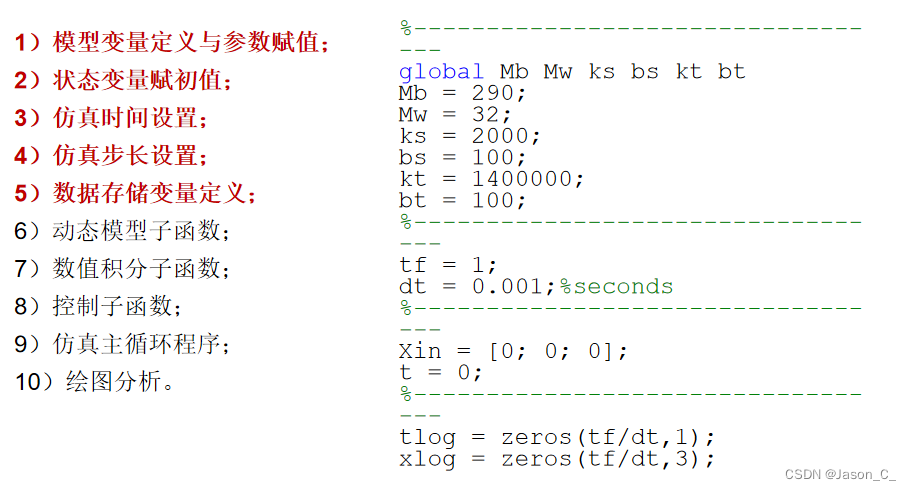
数值积分函数
这里提供了三个选择,matlab中给了4阶龙格库塔和欧拉,大家自行选择

MATLAB代码
clc
clear
clear all
%----------------------------------
global Mb Mw ks bs kt bt
Mb = 290;
Mw = 32;
ks = 20000;
bs = 500;
kt = 1400000;
bt = 100;
%----------------------------------
tf = 1;
dt = 0.001;%seconds
%----------------------------------
Xin = [0; 0; 0];
t = 0;
%----------------------------------
tlog = zeros(tf/dt,1);
xlog = zeros(tf/dt,3);for i = 1: tf/dtu = -0.1 + 0.2*rand; %控制子程序 Xout = Euler(@vdn1,Xin,u,t,dt); %积分函数 tlog(i) = t; %数据存储t = i*dt; %时间更新Xin = Xout; %状态更新xlog(i,:) = Xin'; %数据存储
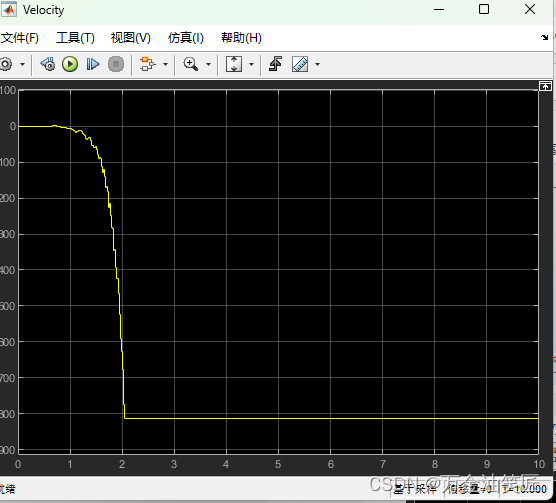
endfigure
subplot(3,1,1)
plot(tlog,xlog(:,1),'k');
ylabel('$z_b \,(m) $');
xlabel('$$ t \, (s) $$');
subplot(3,1,2)
plot(tlog,xlog(:,2),'r');
ylabel('$ {\dot z_b} \,(m) $');
xlabel('$$ t \, (s) $$');
subplot(3,1,3)
plot(tlog,xlog(:,3),'b');
ylabel('$ {z_r} \,(m) $');
xlabel('$$ t \, (s) $$');function dXin = vdn1(t,Xin,u)
global Mb ks bs
%% 状态变量
Zb = Xin(1,:); %车身垂向位移
dZb = Xin(2,:); %车身垂向速度
Zr = Xin(3,:); %路面接触点垂向位移
%% 求状态变量一阶导数
dZr = u(1,:); %路面接触点垂向位移变化率
ddZb = (-bs.*(dZb-dZr)-ks.*(Zb-Zr))/Mb; %车身垂向加速度%% 状态变量一阶导数
dXin = [dZb;ddZb;dZr];
endfunction [y]=runge_kutta4(ufunc,Xin,u,t,h)% ode45
%-----------------------------------------------------------------------------------%
% Author: HUILONG YU, hlyubit@gmail.com.
% Date : 09/11/2016
% Copyright (C) 2016 HUILONG YU. All Rights Reserved.
%-----------------------------------------------------------------------------------%
k1=ufunc(t,Xin,u);
k2=ufunc(t+h/2,Xin+h*k1/2,u);
k3=ufunc(t+h/2,Xin+h*k2/2,u);
k4=ufunc(t+h,Xin+h*k3,u);y=Xin+h*(k1+2*k2+2*k3+k4)/6;
endfunction y = Euler(ufunc,Xin,u,t,h)y= Xin+ h * ufunc(t,Xin,u);
end补充
1、参数中有两个关键参数,决定悬架的“硬度”,【调整悬架参数可抑制路面不平度激励带来的车身振动】
ks = 20000; bs = 500;比 ks = 2000000; bs = 100000; 更好
2、程序每次运行结果不同是因为 输入u 里有一个rand随机数。
Python
环境:Windows ,官网安装的python(安装过程中选择将python添加到全局路径) ,在vscode里直接执行。还需要cmd调出终端安装两个py的模块。
pip install numpy matplotlib
import numpy as np
import matplotlib.pyplot as plt# 全局变量
Mb = 290
Mw = 32
ks = 20000
bs = 500
kt = 1400000
bt = 100# 时间设置
tf = 1
dt = 0.001 # 秒# 初始条件
Xin = np.array([0, 0, 0])
t = 0# 数据存储
tlog = np.zeros(int(tf/dt))
xlog = np.zeros((int(tf/dt), 3))# 定义 vdn1 函数
def vdn1(t, Xin, u):Zb = Xin[0] # 车身垂向位移dZb = Xin[1] # 车身垂向速度Zr = Xin[2] # 路面接触点垂向位移dZr = u # 路面接触点垂向位移变化率ddZb = (-bs * (dZb - dZr) - ks * (Zb - Zr)) / Mb # 车身垂向加速度return np.array([dZb, ddZb, dZr])# 定义 Euler 函数
def Euler(ufunc, Xin, u, t, h):return Xin + h * ufunc(t, Xin, u)# 主循环
for i in range(int(tf/dt)):u = -0.1 + 0.2 * np.random.rand() # 控制子程序Xout = Euler(vdn1, Xin, u, t, dt) # 积分函数tlog[i] = t # 数据存储t = (i + 1) * dt # 时间更新Xin = Xout # 状态更新xlog[i, :] = Xin # 数据存储# 绘图
plt.figure()plt.subplot(3, 1, 1)
plt.plot(tlog, xlog[:, 0], 'k')
plt.ylabel('$z_b \,(m)$')
plt.xlabel('$t \,(s)$')plt.subplot(3, 1, 2)
plt.plot(tlog, xlog[:, 1], 'r')
plt.ylabel('$\dot{z_b} \,(m/s)$')
plt.xlabel('$t \,(s)$')plt.subplot(3, 1, 3)
plt.plot(tlog, xlog[:, 2], 'b')
plt.ylabel('$z_r \,(m)$')
plt.xlabel('$t \,(s)$')plt.tight_layout()
plt.show()相关文章:

MATLAB车辆动力学建模 ——《控制系统现代开发技术》
引言 在上这门课之前,我已经用过CasADi 去做过最优化的相关实践,其中每一步迭代主要就是由:对象系统优化求解两部分组成的。这里我们重点介绍 “对象系统”如何去描述 ,因为它是每一步迭代中重要的一环——“优化求解”会获得控制…...

复杂json解析(其中有一个key的value是json格式的字符串)
app上报的参数如下: {"clientId": "8517895440514039afcf6d3e5d7832ae","dua": "SNDOCKCJPH90_GA&VN900042418&BN0&VCXiaomi&MOM2012K11AC&RL1080_2239&CHIDunknown_unknown&LCID&RV&OSAndroid13&…...
线程池的一些问题
核心线程数1.最大线程5.队列5.存活时间10s 1.场景一 如果核心线程数.被一直占用得不到释放.新进来1个任务.会怎么样?答: 会在队列中中死等. 只要进来的任务.不超过队列的长度,就会一直挡在队列中死等 package com.lin;import java.util.concurrent.Executors; import java.u…...
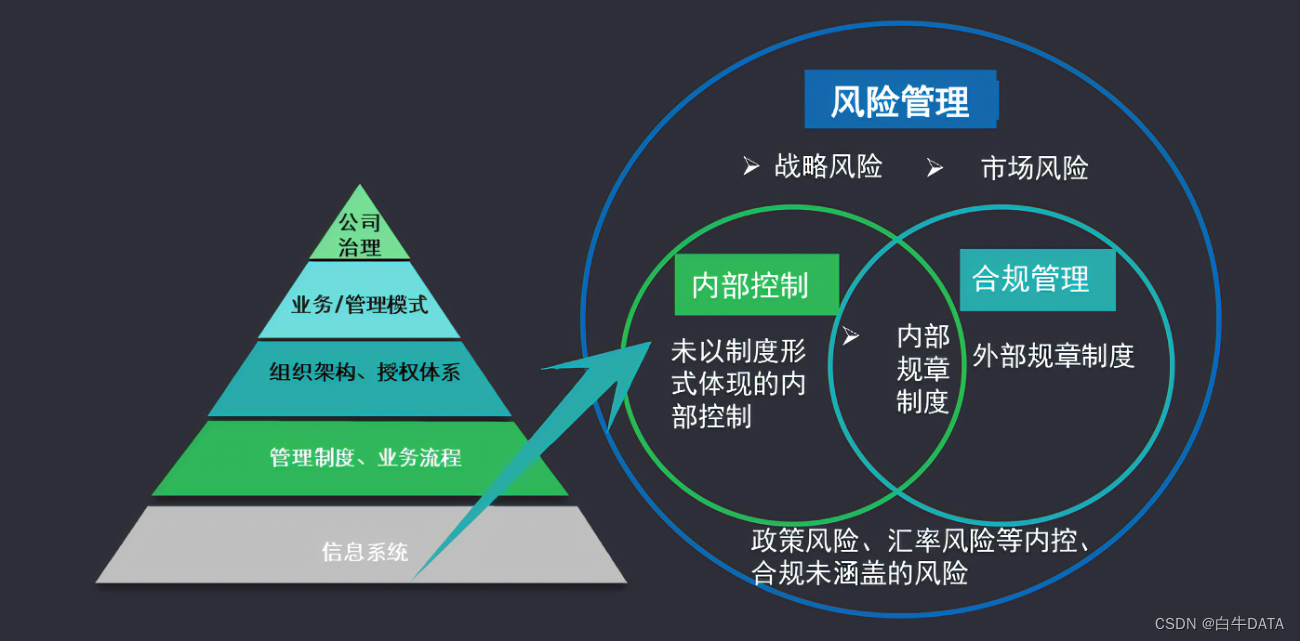
企业或者个体户为什么会经营异常?
在复杂多变的市场经济环境中,无论是企业还是个体工商户,都可能遭遇经营异常的情况。及时识别这些预警信号并采取有效措施,对于避免潜在风险、保持健康发展至关重要。本文将深入探讨企业与个体户常见的经营异常类型、识别方法以及应对策略&…...

ROS从入门到精通4-3:制作Docker镜像文件Dockerfile
目录 0 专栏介绍1 为什么需要Dockerfile?2 Dockerfile书写原则3 Dockerfile常用指令3.1 FROM3.2 MAINTAINER3.3 RUN3.4 ADD3.5 COPY3.6 CMD3.7 ENV3.8 EXPOSE3.9 WORKDIR3.10 ARG 4 Dockerfile构建ROS工程实例 0 专栏介绍 本专栏旨在通过对ROS的系统学习࿰…...

【CV】计算机视觉是什么?
计算机视觉是一门研究如何使机器“看”的学科,旨在实现从图像或视频中获取信息的技术和方法。它涵盖了图像处理、模式识别、机器学习等多个领域,是人工智能领域的重要分支之一。以下是计算机视觉的一般概要介绍: 概要介绍: 图像…...

如何在Vue中实现鼠标悬浮展示与隐藏弹窗的功能
如果你需要鼠标在元素和弹窗上时保持弹窗显示,而鼠标离开这两者时隐藏弹窗,你可以使用一个稍微复杂的逻辑来处理鼠标的进入和离开事件。 这通常涉及到延时关闭弹窗,以便给用户足够的时间从元素移动到弹窗上,而不触发弹窗关闭。以…...
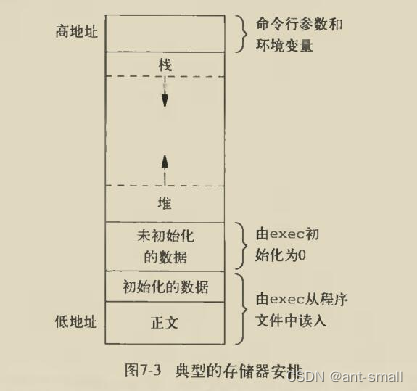
03 Linux编程-进程
1、进程的相关概念 1.1 程序与进程 程序是静态的概念,进程是程序的一次运行活动。 1.2 查看系统中有哪些进程 ps #只显示一小部分进程 ps -aux #会打印当前所有进程 ps -aux|grep init #使用grep筛选出只含有init的进程top #运行显示的进程有点类似windows…...
Hbuild-X运行ios基座app
一、说明 ios真机第一次运行的时候需要下载插件,这个都是自动监测,自动下载的,不用多说。ios真机运行是需要签名的,不然就会报以下错误。如何制作免费的签名证书呢,需要借助爱思助手来完成。 二、安装爱思助手 &…...

Node.js基础:从入门到实战
初识 Node.js 与内置模块 (初识) 1、知道什么是node.js 2、知道node.js可以做什么 3、node.js 中js的组成部分 (内置模块) 4、用 fs 模块读写操作文件 5、使用 path 模块处理路径 6、使用http 模块写一个基本的web服务器 初识 N…...

考研408笔记总结~
目录 一.数据结构 二.计算机组成原理 三.操作系统 四.计算机网络 私以为边看视频,边做笔记会更专注些,大家需要自取。欢迎大家和我一起探讨考研的问题,包括不仅限于专业课,数学,英语等等......,想说什么…...

使用在线工具等方式下载推特视频
使用在线工具等方式下载推特视频 使用在线工具 Visit a Twitter video downloader website: Websites like twdown.net, twittervideodownloader.com, and savevideo.me offer services to download Twitter videos.Paste the Twitter video URL into the designated input bo…...

性能优化:几方面考虑
我们可以继续再考虑下关于性能优化,我们还能从哪些方面着手呢? 1. 代码层面: 使用更高效的数据结构和算法。使用缓存避免多次数据库交互减少不必要的计算和内存分配。利用并行和异步编程提高性能。使用性能分析工具定位和优化瓶颈。 2. We…...

学习大数据:论学习Spark的重要性
随着科技的不断发展,大数据已经成为了当今社会的热门话题。大数据技术的出现,为我们提供了处理海量数据的新方法,使得我们能够从这些数据中挖掘出有价值的信息。在众多的大数据处理框架中,Apache Spark无疑是最为出色的一种。本文…...

学习java第七十一天
DI:依赖注入 依赖注入是spring容器中创建对象时给其设置依赖对象的方式,比如给spring一个清单,清单中列出了需要创建B对象以及其他的一些对象(可能包含了B类型中需要依赖对象),此时spring在创建B对象的时候…...

Altium Designer PCB快捷键设置
6)PCB修改快捷键,并自定义工具栏 添加boardlayerset系统命令。 修改系统脚本, 在D:\Program Files\Altium\AD18\System下,找到advpcb.rcs文件,打开。 Tree MNPCB_LayerSets CaptionManage Layer Se&ts Popup Emp…...
玩转Matlab-Simscape(初级)- 08 - 基于Solidworks、Matlab Simulink、COMSOL的协同仿真(案例实战)
** 玩转Matlab-Simscape(初级)- 08 - 基于Solidworks、Matlab Simulink、COMSOL的协同仿真(案例实战) ** 目录 玩转Matlab-Simscape(初级)- 08 - 基于Solidworks、Matlab Simulink、COMSOL的协同仿真&…...
vue嵌套路由
一、嵌套 children配置 1.父类路由 mymusic 2.子类路由 musicson 1.创建MusicSon组件 <template><div><p>从前和后来</p><p>唯一</p><p>运气来的似有若无</p></div> </template><script>export defaul…...
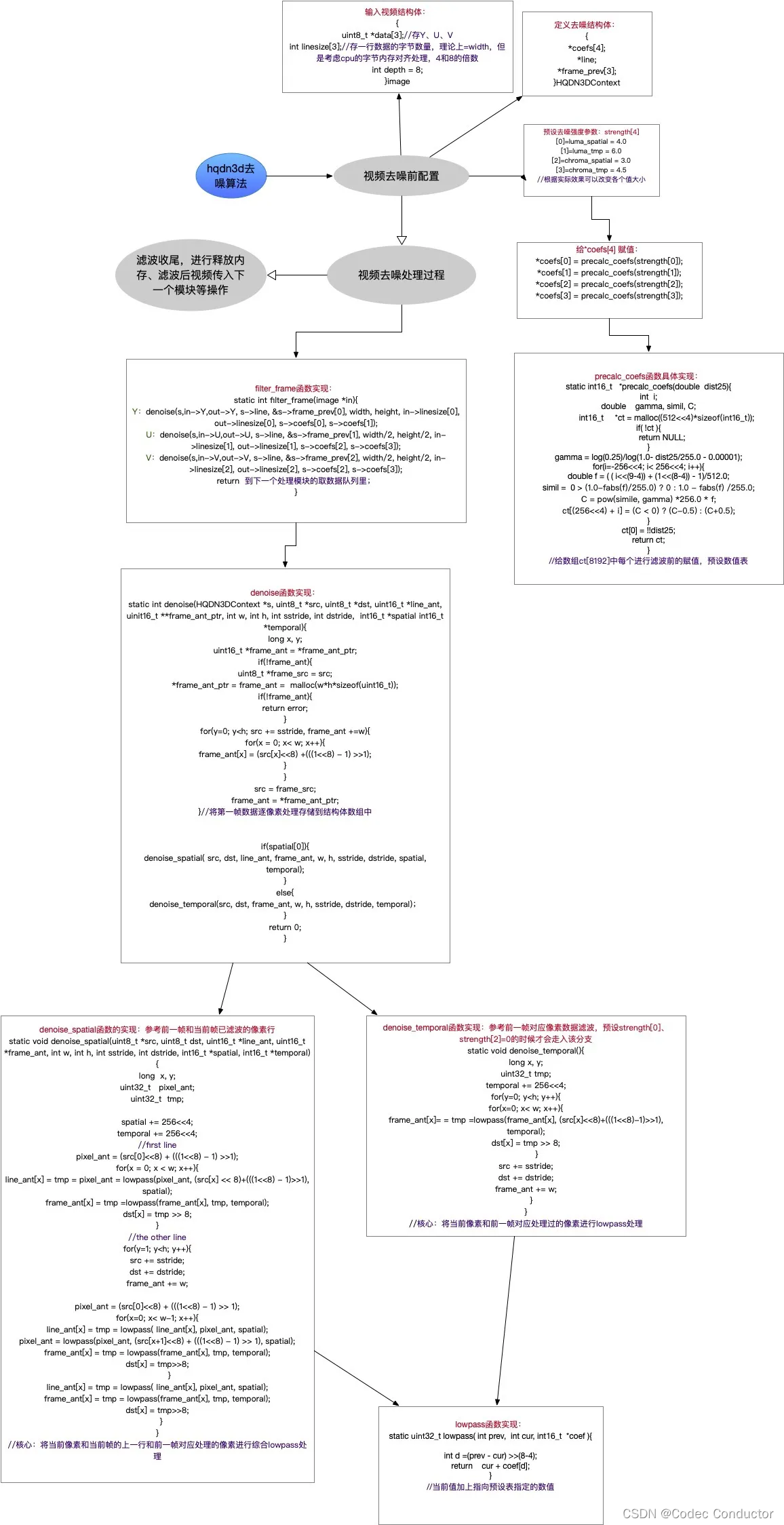
视频降噪算法 hqdn3d 原理分析
视频降噪 视频降噪是一种处理技术,旨在减少视频中的噪声,提高画面质量。噪声可能来自多种源头,包括摄像机的传感器、压缩算法、传输过程中的干扰等。降噪处理对于视频监控、视频会议、电影后期制作以及任何需要高画质输出的应用场景都非常重…...
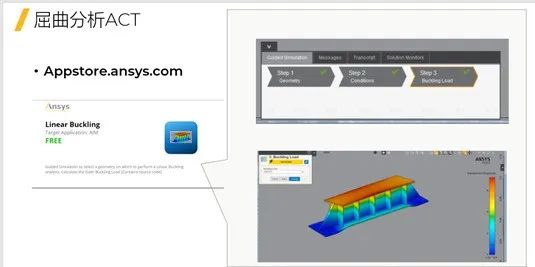
Ansys Mechanical|屈曲分析技术
屈曲分析的基本概念 当受拉杆件的应力达到屈服极限或强度极限时,将引起塑性变形或断裂。这些是由于强度不足所引起的失效。 在工程中,我们会注意到当细长杆件受压时,表现出与强度失效完全不同的性质。当杆件受压超过某一临界值时࿰…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...

CSS | transition 和 transform的用处和区别
省流总结: transform用于变换/变形,transition是动画控制器 transform 用来对元素进行变形,常见的操作如下,它是立即生效的样式变形属性。 旋转 rotate(角度deg)、平移 translateX(像素px)、缩放 scale(倍数)、倾斜 skewX(角度…...

计算机基础知识解析:从应用到架构的全面拆解
目录 前言 1、 计算机的应用领域:无处不在的数字助手 2、 计算机的进化史:从算盘到量子计算 3、计算机的分类:不止 “台式机和笔记本” 4、计算机的组件:硬件与软件的协同 4.1 硬件:五大核心部件 4.2 软件&#…...

Linux部署私有文件管理系统MinIO
最近需要用到一个文件管理服务,但是又不想花钱,所以就想着自己搭建一个,刚好我们用的一个开源框架已经集成了MinIO,所以就选了这个 我这边对文件服务性能要求不是太高,单机版就可以 安装非常简单,几个命令就…...

LCTF液晶可调谐滤波器在多光谱相机捕捉无人机目标检测中的作用
中达瑞和自2005年成立以来,一直在光谱成像领域深度钻研和发展,始终致力于研发高性能、高可靠性的光谱成像相机,为科研院校提供更优的产品和服务。在《低空背景下无人机目标的光谱特征研究及目标检测应用》这篇论文中提到中达瑞和 LCTF 作为多…...

消息队列系统设计与实践全解析
文章目录 🚀 消息队列系统设计与实践全解析🔍 一、消息队列选型1.1 业务场景匹配矩阵1.2 吞吐量/延迟/可靠性权衡💡 权衡决策框架 1.3 运维复杂度评估🔧 运维成本降低策略 🏗️ 二、典型架构设计2.1 分布式事务最终一致…...
