【paper】基于分布式采样的多机器人编队导航信念传播模型预测控制
- Distributed Sampling-Based Model Predictive Control via Belief Propagation for Multi-Robot Formation Navigation
- RAL 2024.4
- Chao Jiang 美国 University of Wyoming
预备知识
马尔可夫随机场(Markov Random Field, MRF)
马尔可夫随机场(MRF)是用于建模多个随机变量之间相互依赖关系的概率图模型。具有以下特点:
- MRF通过无向图表示,节点代表随机变量,边表示变量之间的相互依赖关系。
- 每个节点的条件分布仅依赖于其邻居节点,而不依赖于其他节点。
- 其核心思想是通过局部相互作用来捕捉全局行为。
信念传播(Belief Propagation, BP)
信念传播是一种在图模型(如MRF)上进行推断的算法。它可以用于计算边缘概率分布或最大后验概率估计。主要有两种形式:
- 标准(BP):适用于树结构或无环图。在这些图中,BP可以精确地计算边缘概率分布。
- 循环(Loopy BP):适用于包含环的图。虽然在有环的图中BP不一定收敛或给出精确解,但在实践中它常常表现良好,能提供近似解。
步骤:
- 初始化:将每个节点的初始信念设置为其先验概率。
- 节点之间交换消息,包括关于一个节点的信念如何影响另一个节点。
- 边缘概率计算:通过聚合消息计算每个节点的边缘概率。
Q1 Background:本文试图解决一个什么样的问题?
- 具有复杂系统动力学和不确定性模型的随机最优控制问题
- 多机器人最优轨迹优化问题
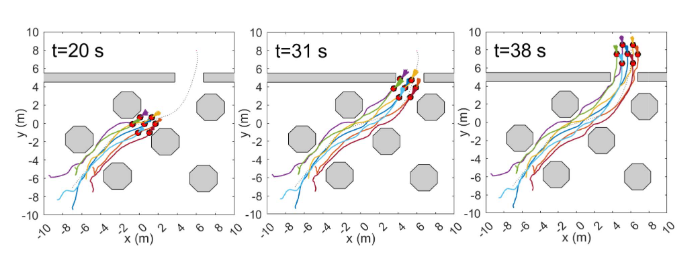
👉20x20的带有静态障碍物的方形环境。轮式机器人数量N=7。初始位置均匀随机分布在左下角的5×5m区域,初始航向从[0,2π)采样。
👉编队目标:使6个机器人将自己定位成正六边形,1个机器人位于编队中心。每个机器人与其最近邻居的距离为1.2m。最大通信范围dmax=1.5 m,最小机器人间距离dmin=0.6 m。最大控制vmax=1.2 m/s。
Q2 What’s Known:之前解决这个问题有哪些方法?
- 基于优化的方法:动态规划 | SCP | MPC
- 缺点:依赖梯度,需要计算导数,不太适合非光滑动力学或成本函数。随着函数的复杂性(例如,非凸性、局部极小值)的增加,这些方法可能变得低效,甚至无法找到可行解。使用基于梯度的优化的现有MPC方法在平滑优化问题中大多是成功的。
- 基于采样的方法:路径积分控制 | 交叉熵 | 信息论MPC | 变分推理MPC
- 定义:使用由前向预测或模拟产生的随机轨迹样本来实现最优控制。
- 优点:不依赖于模型的精确梯度的计算,接受更通用的动力学。随机前向搜索提供了一种解释不确定性的原则性方法,使算法不太容易出现局部极小值。
Q3 What’s New:本文是用什么样的方法如何解决这个问题的?
👉基于分布式采样的MPC算法:将多机器人最优控制公式化为图形模型上的概率推理(probabilistic inference over graphical model),并利用信念传播(leverages belief propagation通过分布式计算实现推理。可以产生基于采样的随机优化的各种分布式最优控制算法。
👉具体Method如下:
建模
-
Model:经典的轮式机器人 - 两轮驱动非完整Robot
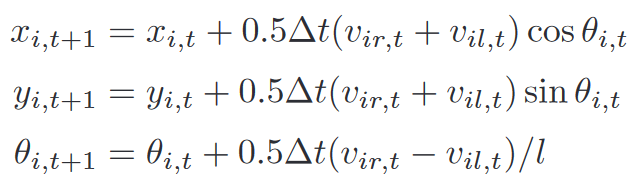
x x x, y y y是2D位置, θ \theta θ是航向角, v l v_l vl和 v r v_r vr代表左轮输入速度和右轮输入速度, l l l是左右轮距离 -
Proximity Graph
无向图,如果 i i i 和 j j j 的欧几里得距离 ≤ d m a x d_{max} dmax(通信范围限制),则 i i i, j j j存在边,且它们俩互为邻居。
所以边集是时变的: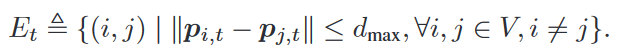
-
避碰和避障
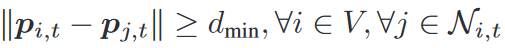
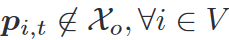
X o \mathcal{X}_o Xo是障碍物占用的位置(膨胀后) -
导航和编队保护
保持编队移动到目标位置,同时避碰
即跟踪参考轨迹 ∥ x i , t − x r , t ∥ , ∀ t ∈ [ 0 , T ] \|x_{i,t}-x_{r,t}\|,\forall t\in[0,T] ∥xi,t−xr,t∥,∀t∈[0,T],参考轨迹 x r , t x_{r,t} xr,t 通过全局运动规划器获得(环境图全局给定),编队由相对位置 Δ p i j \Delta p_{ij} Δpij确定,当所需编队保持不变时,以下等式成立:
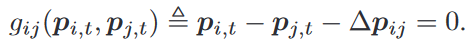
-
MPC轨迹优化问题
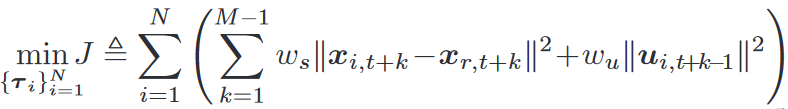
τ i ≜ { x i , t + k , u i , t + k } k = 0 M − 1 \tau_i\triangleq\{x_{i,t+k},u_{i,t+k}\}_{k=0}^{M-1} τi≜{xi,t+k,ui,t+k}k=0M−1是状态控制序列, N N N是智能体数量, M M M是控制时域
key:使用什么样的方法求解这个MPC轨迹优化问题
推理问题
- 目标:找到最优轨迹上的概率分布,从而找到每个机器人的最优控制。
- 概述:首先将多机器人团队建模为一个马尔可夫随机场(MRF)的概率图形模型,然后通过局部消息传递将信念传播(BP)用于分布式推理。最后,开发了一种基于采样的MPC算法来获得每个机器人的最优控制。
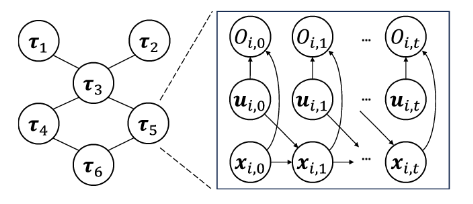
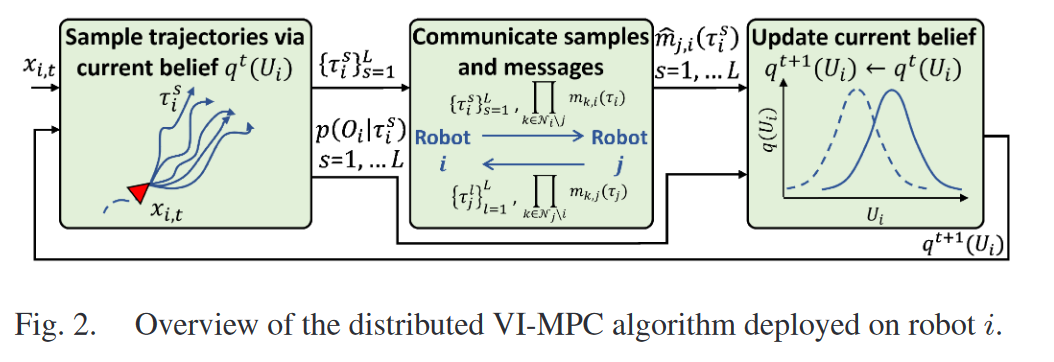
- 采样轨迹
输入: t t t时刻状态 x x x和当前的置信分布 q ( U ) q(U) q(U)
根据 q ( U ) q(U) q(U)对轨迹 τ \tau τ进行采样,得到 L L L个样本
计算每个样本轨迹的观测似然 p ( O ∣ τ ) p(O|\tau) p(O∣τ)- 传递样本轨迹和消息
i i i 发送轨迹样本给邻居 j j j,并接受邻居 j j j的轨迹样本
i i i 计算并传递消息 m k , i ( τ ) m_{k,i}(\tau) mk,i(τ)( i i i除了 j j j外的所有邻居 k k k对轨迹 τ i \tau_i τi的估计
i i i 接受 j j j 计算的消息( j j j除了 i i i外的所有邻居 k k k对轨迹 τ j \tau_j τj的估计- 更新当前置信分布
根据收到的所有邻居机器人的消息和当前时刻的观测信息更新当前的置信分布 q ( U ) q(U) q(U)

Q4 What’s the Contribution:本文还有什么其他的贡献吗?
- 主要贡献是完全分布式框架,每个机器人只需要局部信息。它将基于采样的优化方法[6]、[7]、[8]、[9]、[10]扩展到多机器人问题。
- 对比CMPC,计算速度快
- 对比基于ADMM求解的MPC,计算速度快且成功率高(分别为82%和98%)
Q5 What’s the Inspiration
- 模型比较常规,文章重点在于怎么求解问题,把基于采用的随机最优控制(变分推理)用到了求解DMPC问题中,核心思想还是每个机器人根据其他机器人的信息和自己的观测不断调整和优化自身的轨迹,达到全局最优的控制目标。
- 求解都比较数学,MRF和BP的地方没太看懂,这部分对我的工作没太大用处,但如果有人能看懂这个数学部分把他做到无人机再加个真机实验应该能写个好文章
相关文章:

【paper】基于分布式采样的多机器人编队导航信念传播模型预测控制
Distributed Sampling-Based Model Predictive Control via Belief Propagation for Multi-Robot Formation NavigationRAL 2024.4Chao Jiang 美国 University of Wyoming 预备知识 马尔可夫随机场(Markov Random Field, MRF) 马尔可夫随机场ÿ…...

代码随想录算法训练营第二天| 977.有序数组的平方 、209.长度最小的子数组、 59.螺旋矩阵II
977. 有序数组的平方 题目链接:977. 有序数组的平方 文档讲解:代码随想录 状态:so easy 刚开始看到题目第一反应就是平方之后进行排序,数据量在 1 0 4 10^4 104,可以使用O(nlogn)的排序。但是更好的方式是使用双指针&a…...

list stream 改变list属性的值
在Java中,如果你想使用Stream API来改变List中对象的某个属性值,需要注意的是,Stream API本身设计为不可变操作,即它不直接修改原有的集合,而是产生一个新的流或集合。但是,你可以通过流操作来创建一个新的…...

绿色智能:AI机器学习在环境保护中的深度应用与实践案例
🧑 博主简介:阿里巴巴嵌入式技术专家,深耕嵌入式人工智能领域,具备多年的嵌入式硬件产品研发管理经验。 📒 博客介绍:分享嵌入式开发领域的相关知识、经验、思考和感悟,欢迎关注。提供嵌入式方向…...
)
Java高级面试精粹:问题与解答集锦(二)
Java面试问题及答案 1. 什么是Java内存模型(JMM)?它的作用是什么? 答案: Java内存模型(JMM)定义了Java虚拟机(JVM)在计算机内存中的工作方式,包括程序计数器…...

基于机器学习模型预测信用卡潜在用户(XGBoost、LightGBM和Random Forest)
基于机器学习模型预测信用卡潜在用户(XGBoost、LightGBM和Random Forest) 随着数据科学和机器学习的发展,越来越多的企业开始利用这些技术来提高运营效率。在这篇博客中,我将分享如何利用机器学习模型来预测信用卡的潜在客户。此…...
)
java 通过 microsoft graph 调用outlook(三)
这次会添加一个Reply接口, 并且使用6.10.0版本 直接上代码 一, POM <!-- office 365 --><dependency><groupId>com.microsoft.graph</groupId><artifactId>microsoft-graph</artifactId><version>6.1…...
QT--TCP网络通讯工具编写记录
QT–TCP网络通讯工具编写记录 文章目录 QT--TCP网络通讯工具编写记录前言演示如下:一、服务端项目文件:【1.1】server_tcp.h 服务端声明文件【1.2】thread_1.h 线程处理声明文件【1.3】main.cpp 执行源文件【1.4】server_tcp.cpp 服务端逻辑实现源文件【…...

如何解决爬虫的IP地址受限问题?
使用代理IP池、采用动态IP更换策略、设置合理的爬取时间间隔和模拟正常用户行为,是解决爬虫IP地址受限问题的主要策略。代理IP池是通过集合多个代理IP来分配爬虫任务,从而避免相同的IP地址对目标网站进行高频次访问,减少被目标网站封禁的风险…...

harmony 文件上传
图片上传 1, 获取文件,这里指的是图片 在鸿蒙内部有一个API pick选择器,实现文件保存和文件选择的功能, 使用pick对象创建PhotoViewPicker实例 传入必要的参数,如选择图片的数量,和弹出窗口的位置…...

什么是安全左移如何实现安全左移
文章目录 一、传统软件开发面临的安全挑战二、什么是安全左移四、安全左移与安全开发生命周期(SDL)三、安全左移对开发的挑战五、从DevOps到DevSecOps六、SDL与DevSecOps 一、传统软件开发面临的安全挑战 传统软件开发面临的安全挑战主要包括以下几个方…...

将PCD点云投影到BEV平面得到图片
前言 点云数据作为一种丰富的三维空间信息表达方式,通常用于自动驾驶、机器人导航和三维建模等领域。然而,点云数据的直观性不如二维图像,这限制了它在一些需要快速视觉反馈的应用场景中的使用。本文将探讨如何将点云数据转换为二维图像&…...
)
计算机笔记14(续20个)
230.色彩的种类就是色相 饱和度就是彩度除以明度 231.RISC是精简指令集,CISC是复杂指令集 232.世界上第一台数字计算机,奠定了至今仍在使用计算机体系结构 233.数据传输中,电路交换的传输延迟最小 234.定点整数的小数点约定在最低…...

docker 使用桥接网
在Docker中使用桥接网络,你可以创建一个新的桥接网络或者使用默认的桥接网络(如果已经存在的话)。以下是创建新桥接网络和连接容器到这个网络的示例命令: 1.创建一个新的桥接网络(如果你想创建一个新的)&a…...

1金融风控相关业务介绍
金融风控相关业务介绍 学习目标 知道常见信贷风险知道机器学习风控模型的优势知道信贷领域常用术语含义1 信贷&风控介绍 信贷业务,就是贷款业务,是商业银行和互联网金融公司最重要的资产业务和主要赢利手段 通过放款收回本金和利息,扣除成本后获得利润。贷款平台预测有…...

521源码-免费教程-经常用到的Vue.js的Vue@Cli入门指导
更多网站源码学习教程,请点击👉-521源码-👈获取最新资源:521源码-网站源码-资源素材-免费下载 Vue.js是一款流行的JavaScript框架,它使得构建交互式的Web界面变得简单和快捷。VueCli是Vue.js官方提供的脚手架工具&…...

大数据技术原理(二):搭建hadoop伪分布式集群这一篇就够了
(实验一 搭建hadoop伪分布式) -------------------------------------------------------------------------------------------------------------------------------- 一、实验目的 1.理解Hadoop伪分布式的安装过程 实验内容涉及Hadoop平台的搭建和…...

中间件是什么?信创中间件有哪些牌子?哪家好用?
当今社会,中间件的重要性日益凸显,尤其是在信创背景下,选择适合的中间件产品对于推动企业数字化转型和升级具有重要意义。今天我们就来聊聊中间件是什么?信创中间件有哪些牌子?哪家好用?仅供参考哈…...

python实现520表白图案
今天是520哦,作为程序员有必要通过自己的专业知识来向你的爱人表达下你的爱意。那么python中怎么实现绘制520表白图案呢?这里给出方法: 1、使用图形库(如turtle) 使用turtle模块,你可以绘制各种形状和图案…...
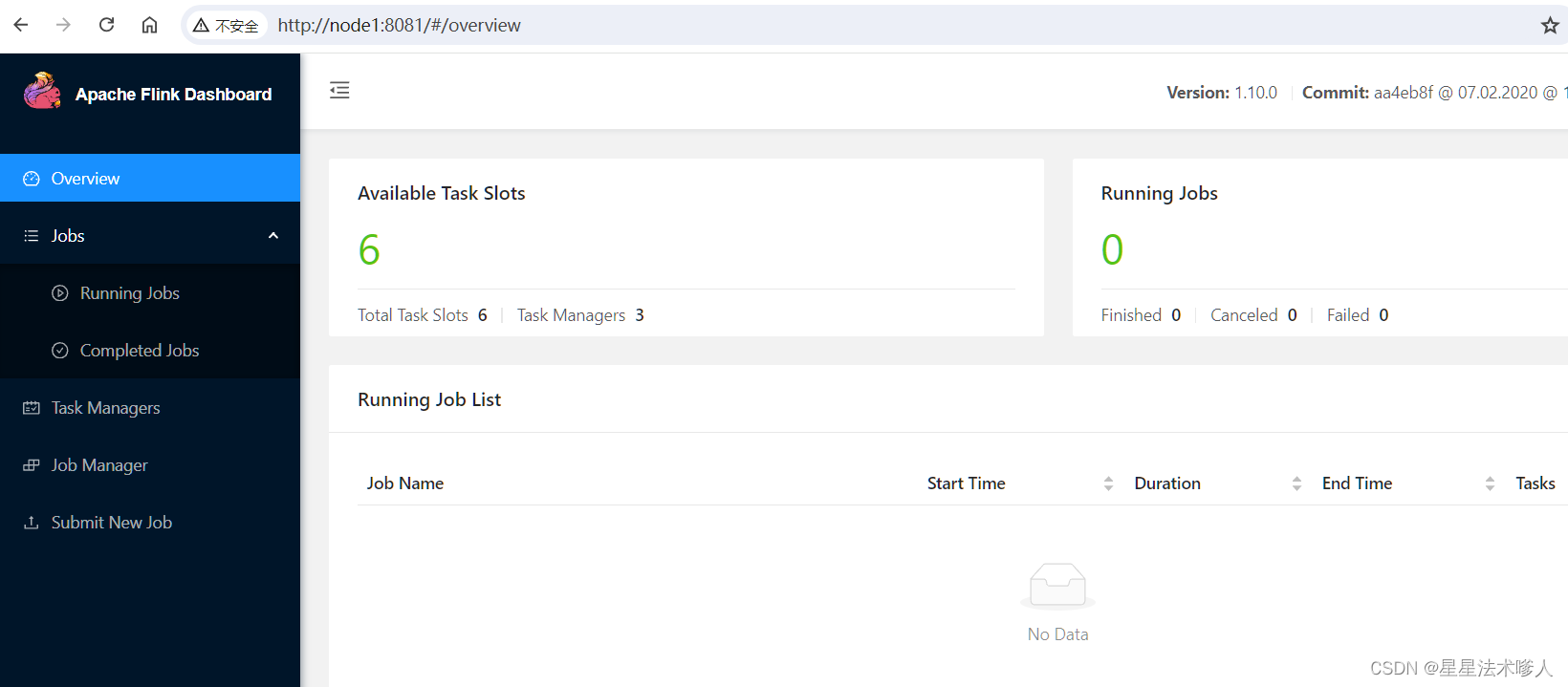
【Linux】-Flink分布式内存计算集群部署[21]
注意: 本节的操作,需要前置准备好Hadoop生态集群,请先部署好Hadoop环境 简介 Flink同spark一样,是一款分布式内存计算引擎,可以支撑海量数据的分布式计算 Flink在大数据体系同样是明星产品,作为新一代的…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...
