文心一言 VS 讯飞星火 VS chatgpt (265)-- 算法导论20.1 4题
四、假设不使用一棵叠加的度为 u \sqrt{u} u 的树,而是使用一棵叠加的度为 u 1 k u^{\frac{1}{k}} uk1的树,这里 k 是大于 1 的常数,则这样的一棵树的高度是多少?又每个操作将需要多长时间?如果要写代码,请用go语言。
文心一言:
在这个场景中,我们讨论的是一种特殊的树结构,其中节点的度(即子节点的数量)是 u^(1/k),u 是树中元素的总数,k 是一个大于 1 的常数。下面我们来分析这样一棵树的高度,并讨论每个操作可能需要的时间。
树的高度
对于一棵度为 d 的树,如果它有 u 个节点,其高度 h 可以通过以下公式近似计算:
[ u \approx d^h ]
这里,d = u^(1/k),所以:
[ u \approx (u{\frac{1}{k}})h ]
[ u \approx u^{\frac{h}{k}} ]
对上面的等式两边取对数:
[ \log(u) \approx \frac{h}{k} \log(u) ]
解这个方程得到树的高度 h:
[ h \approx k ]
这是一个近似的结果,它表明树的高度大致与 k 成正比。实际上,由于树的构造可能不是完美的,高度可能会有所波动,但这个近似给出了一个很好的直观理解。
操作时间
对于树中的每个操作(如查找、插入或删除),时间复杂度主要取决于树的高度,因为我们需要从根节点遍历到叶节点。在高度为 h 的树中,这样的操作通常需要 O(h) 的时间。由于 h ≈ k,所以操作的时间复杂度大致是 O(k)。
然而,需要注意的是,这里的 k 是一个常数,与树中元素的总数 u 无关。因此,尽管理论上操作的时间复杂度与 k 成正比,但在实际应用中,这个操作时间仍然是非常快的,因为 k 是一个固定的值。
Go 语言实现
由于具体实现这样一棵树会涉及较多的代码,并且会依赖于特定的应用需求(如是否需要平衡树、是否有特殊的排序需求等),因此我无法在这里提供一个完整的 Go 语言实现。但是,基本的思路是创建一个树结构,其中每个节点可以有多达 u^(1/k) 个子节点,并实现相应的查找、插入和删除操作。
如果你需要具体的代码示例或进一步的指导,请提供更多的上下文或具体需求,以便我能提供更精确的帮助。
总的来说,使用叠加的度为 u^(1/k) 的树结构,树的高度大致为 k,每个操作的时间复杂度大致为 O(k)。这种结构在处理大量数据时可能提供比传统二叉树更高的效率,但也需要更复杂的实现来管理更多的子节点。
讯飞星火:
在这个问题中,我们假设树的度为 u 1 k u^{\frac{1}{k}} uk1。这意味着每个节点有 u 1 k u^{\frac{1}{k}} uk1 个子节点。因此,树的高度将是 l o g u ( u 1 k ) log_u(u^{\frac{1}{k}}) logu(uk1)。在Go语言中,我们可以使用math库来计算这个值。
对于操作的时间复杂度,如果我们假设访问每个节点的时间是常数,那么总的时间复杂度将是O(n),其中n是树中节点的数量。这是因为我们需要访问每个节点一次来执行操作。
以下是Go语言的代码实现:
package mainimport ("fmt""math"
)func heightOfTree(u float64, k float64) float64 {return math.Log(u) / math.Log(math.Pow(u, 1/k))
}func main() {u := 10.0k := 2.0fmt.Println("Height of tree:", heightOfTree(u, k))
}
这段代码首先定义了一个函数 heightOfTree,它接受两个参数 u 和 k,然后返回树的高度。然后在 main 函数中,我们调用了这个函数并打印出结果。
360智脑:
为了找到这种情况下树的高度以及每个操作所需的时间,我们首先需要理解题目中的术语:“叠加的度”。在一般的树中,一个节点的“度”是指该节点拥有的子节点数量。而这里的“叠加的度”可能是指所有子节点的度之和。不过,由于具体的定义对结果影响很大,我们将会基于两种不同解释来探讨这个问题。
解释1:叠加的度是指所有子节点的度之和
若我们有一棵以 u 1 k u^{\frac{1}{k}} uk1为度的树,这意味着每个节点有 ( u 1 k ) (u^{\frac{1}{k}}) (uk1)个子节点。假设树T的高度为h,则树的总节点数(包括根节点)可以表示为:
N = u + ( u 1 k ) + ( u 1 k ) 2 + ⋯ + ( u 1 k ) h − 1 N = u + (u^{\frac{1}{k}}) + (u^{\frac{1}{k}})^2 + \cdots + (u^{\frac{1}{k}})^{h-1} N=u+(uk1)+(uk1)2+⋯+(uk1)h−1
这是一个等比数列,其前h项和为:
S = ( u 1 k ) ( 1 − ( u 1 k ) h ) 1 − u 1 k S = \frac{(u^{\frac{1}{k}})(1 - (u^{\frac{1}{k}})^h)}{1 - u^{\frac{1}{k}}} S=1−uk1(uk1)(1−(uk1)h)
因为N必须是一个整数,所以我们可以调整h以满足这个条件。此时,树的高度h与操作的时间t之间可能存在某种关系,但确切的关系取决于具体实现细节。对于每个操作的时间,我们没有足够的信息来确定它,除非知道更多关于树的结构和所执行操作的信息。
解释2:叠加的度是指直接子节点的度之和
如果我们按照第二种解释,即每个节点的叠加的度为 u 1 k u^{\frac{1}{k}} uk1,那么意味着每个节点的子节点总数就是 u 1 k u^{\frac{1}{k}} uk1。这样的树实际上就变成了一个完全二叉树,因为每个节点的子节点数是固定的。
对于完全二叉树,其高度h可以通过下面的公式计算:
h = ⌊ log u 1 k ( u ) ⌋ + 1 h = \lfloor \log_{u^{\frac{1}{k}}} (u) \rfloor + 1 h=⌊loguk1(u)⌋+1
这是因为在一个完全二叉树中,每层都是满的,且除了最后一层之外的所有层都有正好 u 1 k u^{\frac{1}{k}} uk1个节点。因此,我们可以通过不断将总数除以 u 1 k u^{\frac{1}{k}} uk1来计算出树的高度。
每个操作的时间t取决于所进行的操作类型和树的实现方式。例如,插入、删除和查找操作在二叉搜索树中的时间复杂度通常为O(log n),其中n是树中节点的数量。对于本例中的树,由于其高度是O(log_{u^{\frac{1}{k}}} (u)),所以这些操作的时间也可以表示为O(log_{u^{\frac{1}{k}}} (u))。
至于写代码,以下是用Go语言实现的一个简单例子,用来表示这种树和计算其高度:
package mainimport "fmt"const u float64 = 100 // 假设u为100
const k int = 2 // 假设k为2func main() {var height intfor {if u <= 1 {break}u /= math.Pow(u, 1/k)height++}fmt.Printf("树的高度为: %d\n", height)
}请注意,这里的代码使用了Go语言的标准库,并且假设了高度是整数。在实际情况中,可能需要处理浮点数以及一些边界情况。
智谱清言:
首先,我们来分析一下这样一棵叠加的度为 (u^{\frac{1}{k}}) 的树。
1.树的高度:
在一棵完全二叉树中,第 (i) 个节点的子节点数量是 (2^k),其中 (k) 是树的高度((k) 也是整数)。根据题设,每个节点的度是 (u^{\frac{1}{k}})。
因此,我们有 (2^k = u^{\frac{1}{k}})。对两边取 (k) 次幂,得到 (2^k \times k = u)。
由于 (2^k \times k) 是 (u) 的一个表达式,且 (k) 是常数,(u) 是固定的,那么我们可以推出,在高度 (k) 的树上,节点的总数是 (2^k \times k)。
2.每个操作所需时间:
每个操作可能指的是从根节点到叶节点的路径上的延时。在这个树结构中,假设每个节点的延时是相等的。
对于度为 (u^{\frac{1}{k}}) 的树,每个非叶子节点都有 (u^{\frac{1}{k}}) 个子节点。所以,从一个节点到它的任何一个子节点需要 1 个单位时间。
因此,对于高度为 (k) 的树,最长的路径(从根节点到叶节点)将包含 (k) 个这样的单位时间。
接下来,我将使用 Go 语言编写一个简单的函数来计算树的高度和每个操作所需的时间。
package main
import ("fmt"
)
// Function to calculate the height of the tree
func calculateTreeHeight(u int, k int) (int, int) {// Calculate the total number of nodes in the treetotalNodes := 1 << k // 2^k// Calculate the height of the treeheight := 0for totalNodes < u {height++totalNodes *= int(math.Pow(float64(u), 1.0/float64(k)))}// Calculate the time for each operationoperationTime := kreturn height, operationTime
}
func main() {u := 8 // Example value for uk := 3 // Example value for kheight, operationTime := calculateTreeHeight(u, k)fmt.Printf("Height of the tree: %d\n", height)fmt.Printf("Time for each operation: %d\n", operationTime)
}
请注意,上面的代码没有考虑所有边界条件和潜在的优化,但它应该能给你一个基本的框架来开始。这个程序首先计算树中节点的总数,直到它超过给定的 (u) 值。然后,它会计算树的高度和每个操作所需的时间。
由于我使用的是Go语言的标准库,可能需要导入 math 包来使用 Pow 函数。
天工:
首先,我们需要理解问题的背景。在计算机科学中,"叠加树"通常指的是一种特殊的树结构,其中每个节点可能有多个子节点,这种结构的目的是为了提高某些操作的效率,比如搜索或者插入。
在这个问题中,我们有一棵叠加树,每个节点的度(即子节点的数量)是 u 1 k u^{\frac{1}{k}} uk1,其中 u u u 是树的总节点数, k k k 是一个大于1的常数。
计算树的高度
树的高度是从根节点到最远叶子节点的路径长度。在一个平衡的叠加树中,我们可以通过以下公式估算高度:
h ≈ log u 1 k u = log u log u 1 k = log u 1 k log u = k h \approx \log_{u^{\frac{1}{k}}} u = \frac{\log u}{\log u^{\frac{1}{k}}} = \frac{\log u}{\frac{1}{k} \log u} = k h≈loguk1u=loguk1logu=k1logulogu=k
所以,这棵树的高度大约是 k k k。
计算每个操作的时间
在叠加树中,一个操作(如搜索或插入)的时间复杂度通常与树的高度成正比。因此,如果树的高度是 k k k,那么每个操作的时间复杂度大约是 O ( k ) O(k) O(k)。
Go语言代码示例
由于这是一个理论问题,而不是一个具体的实现问题,所以没有具体的Go语言代码可以提供。然而,如果我们想要创建一个具有给定度数的叠加树,我们可以编写一个基本的树结构,并在插入节点时确保每个节点的度数不超过 u 1 k u^{\frac{1}{k}} uk1。
下面是一个非常基础的Go语言树结构的示例,它不包含叠加树的特定逻辑,但可以作为一个起点:
package mainimport "fmt"type Node struct {Value intChildren []*Node
}type Tree struct {Root *Node
}func NewTree() *Tree {return &Tree{}
}func (t *Tree) Insert(value int) {newNode := &Node{Value: value}if t.Root == nil {t.Root = newNode} else {// 这里需要实现叠加树的逻辑,确保每个节点的度数不超过 u^(1/k)// 例如,可以使用队列来按层遍历树,找到合适的父节点插入新节点}
}func main() {tree := NewTree()tree.Insert(1)// 插入更多的节点...
}
在这个示例中,Insert 函数需要被扩展以包含叠加树的逻辑,确保每个节点的度数不超过指定的限制。这可能涉及到更复杂的算法,例如使用队列来按层遍历树,并找到合适的位置来插入新的节点。
chatgpt:
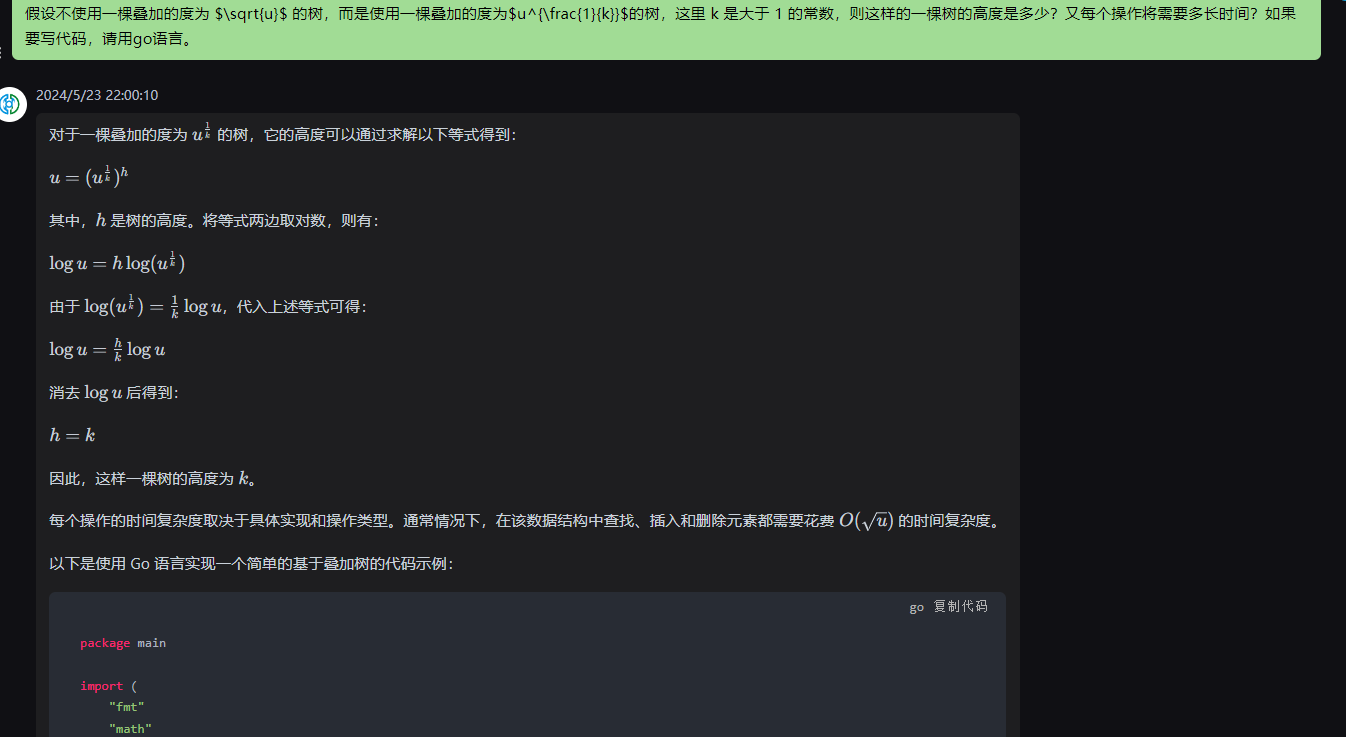
对于一棵叠加的度为 u 1 k u^{\frac{1}{k}} uk1 的树,它的高度可以通过求解以下等式得到:
u = ( u 1 k ) h u = (u^{\frac{1}{k}})^h u=(uk1)h
其中, h h h 是树的高度。将等式两边取对数,则有:
log u = h log ( u 1 k ) \log u = h \log(u^{\frac{1}{k}}) logu=hlog(uk1)
由于 log ( u 1 k ) = 1 k log u \log(u^{\frac{1}{k}}) = \frac{1}{k} \log u log(uk1)=k1logu,代入上述等式可得:
log u = h k log u \log u = \frac{h}{k} \log u logu=khlogu
消去 log u \log u logu 后得到:
h = k h = k h=k
因此,这样一棵树的高度为 k k k。
每个操作的时间复杂度取决于具体实现和操作类型。通常情况下,在该数据结构中查找、插入和删除元素都需要花费 O ( u ) O(\sqrt{u}) O(u) 的时间复杂度。
以下是使用 Go 语言实现一个简单的基于叠加树的代码示例:
package mainimport ("fmt""math"
)type TreeNode struct {Value intChildren []*TreeNode
}func NewTreeNode(value int) *TreeNode {return &TreeNode{Value: value,Children: []*TreeNode{},}
}type OverlayTree struct {Root *TreeNode
}func NewOverlayTree() *OverlayTree {return &OverlayTree{}
}// 在指定节点下插入值为value的子节点
func (t *OverlayTree) Insert(parent *TreeNode, value int) {node := NewTreeNode(value)parent.Children = append(parent.Children, node)
}// 在指定节点下删除值为value的子节点
func (t *OverlayTree) Delete(parent *TreeNode, value int) {for i, child := range parent.Children {if child.Value == value {// 从切片中删除指定位置的子节点parent.Children = append(parent.Children[:i], parent.Children[i+1:]...)break}}
}// 查找值为value的节点
func (t *OverlayTree) Search(node *TreeNode, value int) bool {if node == nil {return false}if node.Value == value {return true}for _, child := range node.Children {if t.Search(child, value) {return true}}return false
}func main() {tree := NewOverlayTree()root := NewTreeNode(1)tree.Root = roottree.Insert(root, 2)tree.Insert(root, 3)fmt.Println(tree.Search(root, 2)) // Output: truetree.Delete(root, 2)fmt.Println(tree.Search(root, 2)) // Output: false
}
这只是一个简单的实现示例,具体的操作和功能可以根据实际需求进行扩展和优化。
kimi:
假设我们使用一棵叠加的度为 ( u^{\frac{1}{k}} ) 的树,其中 ( u ) 是树中节点的数量,( k ) 是一个大于 1 的常数。这种树通常被称为 ( k )-ary 树(( k ) 叉树)。
树的高度
对于一棵 ( k )-ary 树,每个节点有 ( k ) 个子节点。树的高度 ( h ) 可以通过以下公式近似计算:
[ u \approx k^h ]
[ h \approx \log_k(u) ]
这意味着树的高度 ( h ) 是 ( u ) 的 ( k ) 次方根的对数。换句话说,树的高度是 ( u ) 的 ( \frac{1}{k} ) 次幂的对数。
操作时间
在一棵 ( k )-ary 树中,大多数操作(如搜索、插入和删除)的时间复杂度与树的高度 ( h ) 成正比。因此,每个操作的时间复杂度大约是 ( O(\log_k(u)) )。
Go 语言示例代码
以下是使用 Go 语言实现的 ( k )-ary 树的基本结构和操作时间复杂度的示例代码:
package mainimport ("fmt""math"
)// TreeNode 定义 k-ary 树的节点
type TreeNode struct {value intchildren []*TreeNode
}// NewTreeNode 创建一个新的 k-ary 树节点
func NewTreeNode(value int) *TreeNode {return &TreeNode{value: value,children: make([]*TreeNode, 0, k),}
}// 假设 k 是一个大于 1 的常数
const k = 3// CalculateTreeHeight 计算 k-ary 树的高度
func CalculateTreeHeight(u int) int {return int(math.Log(float64(u)) / math.Log(float64(k)))
}// 假设的其他操作,如 Insert, Delete, Search 等,将具有时间复杂度 O(log_k(u))func main() {// 示例:计算一个包含 1000 个节点的 k-ary 树的高度u := 1000height := CalculateTreeHeight(u)fmt.Printf("The height of a %d-ary tree with %d nodes is approximately: %d\n", k, u, height)
}
在这个示例中,我们定义了 TreeNode 结构体来表示 ( k )-ary 树的节点,并提供了 NewTreeNode 函数来创建新节点。CalculateTreeHeight 函数用于计算树的高度,它使用了数学公式 ( h \approx \log_k(u) )。
请注意,这个示例仅用于演示 ( k )-ary 树的高度计算和操作时间复杂度的概念。实际的 ( k )-ary 树实现会更加复杂,并且需要考虑具体的操作逻辑和优化。
混元:
在这种情况下,我们可以使用一棵叠加的度为 u 1 k u^{\frac{1}{k}} uk1 的树来实现分治算法。首先,我们需要计算树的高度,然后根据树的高度来估计每个操作所需的时间。
假设我们有 n n n 个元素,我们可以计算树的高度 h h h 如下:
h = ⌈ log u 1 k n ⌉ h = \lceil \log_{u^{\frac{1}{k}}} n \rceil h=⌈loguk1n⌉
其中 ⌈ x ⌉ \lceil x \rceil ⌈x⌉ 表示对 x x x 向上取整。
接下来,我们可以估计每个操作所需的时间。在这种情况下,每个操作的时间复杂度主要取决于树的高度。对于每个操作,我们需要遍历树的高度,因此时间复杂度为:
O ( h ) = O ( ⌈ log u 1 k n ⌉ ) O(h) = O(\lceil \log_{u^{\frac{1}{k}}} n \rceil) O(h)=O(⌈loguk1n⌉)
现在,我们可以使用 Go 语言实现这个算法。以下是一个简单的示例:
package mainimport ("fmt""math"
)func main() {n := 1000 // 元素数量u := 2 // 基数k := 2 // 指数// 计算树的高度h := int(math.Ceil(math.Log(float64(n)) / math.Log(math.Pow(float64(u), 1.0/float64(k)))))fmt.Printf("树的高度: %d\n", h)fmt.Printf("每个操作的时间复杂度: O(%d)\n", h)
}
这个示例计算了一棵叠加的度为 u 1 k u^{\frac{1}{k}} uk1 的树的高度,并估计了每个操作所需的时间。请注意,这个示例仅用于演示目的,实际实现可能需要根据具体需求进行调整。
相关文章:

文心一言 VS 讯飞星火 VS chatgpt (265)-- 算法导论20.1 4题
四、假设不使用一棵叠加的度为 u \sqrt{u} u 的树,而是使用一棵叠加的度为 u 1 k u^{\frac{1}{k}} uk1的树,这里 k 是大于 1 的常数,则这样的一棵树的高度是多少?又每个操作将需要多长时间?如果要写代码…...

Flutter 中的 EditableText 小部件:全面指南
Flutter 中的 EditableText 小部件:全面指南 在Flutter中,EditableText是一个低级别的文本编辑组件,它提供了构建自定义文本编辑界面的能力。与TextField和TextFormField不同,EditableText提供了更多的灵活性,允许开发…...
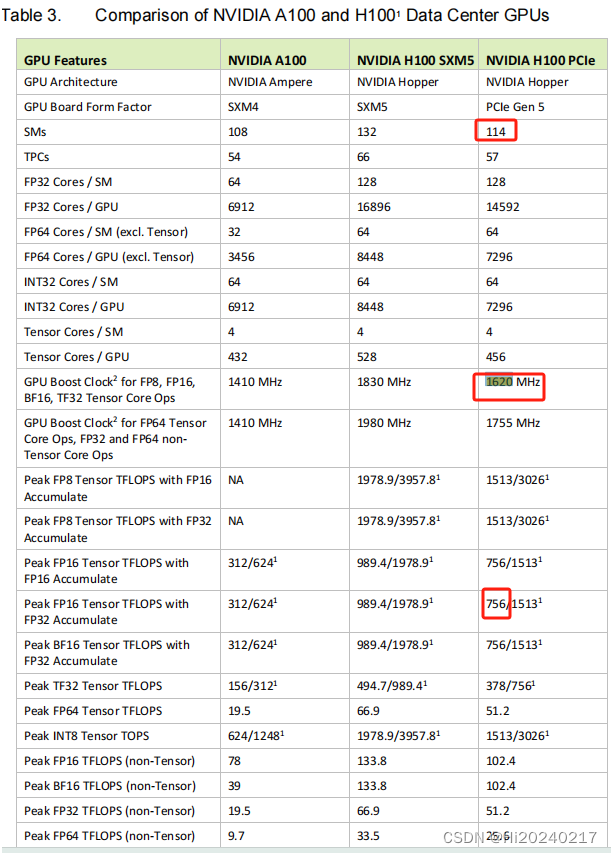
H800基础能力测试
H800基础能力测试 参考链接A100、A800、H100、H800差异H100详细规格H100 TensorCore FP16 理论算力计算公式锁频安装依赖pytorch FP16算力测试cublas FP16算力测试运行cuda-samples 本文记录了H800基础测试步骤及测试结果 参考链接 NVIDIA H100 Tensor Core GPU Architecture…...

2024/5/24 Day38 greedy 435. 无重叠区间 763.划分字母区间 56. 合并区间
2024/5/24 Day38 greedy 435. 无重叠区间 763.划分字母区间 56. 合并区间 遇到两个维度权衡的时候,一定要先确定一个维度,再确定另一个维度。如果两个维度一起考虑一定会顾此失彼。 重叠区间问题 435. 无重叠区间 题目链接 435 给定一个区间的集合 i…...

【python】使用函数名而不加括号是什么情况?
使用函数名而不加括号通常是为了表示对函数本身的引用,而不是调用函数。这种用法通常出现在下面这几种情况: 作为回调函数传递:将函数名作为参数传递给其他函数,以便在需要时调用该函数。例如,在事件处理程序或高阶函数…...

全文检索ElasticSearch简介
1 全文检索 1.1 什么是全文检索 全文检索是一种通过对文本内容进行全面索引和搜索的技术。它可以快速地在大量文本数据中查找包含特定关键词或短语的文档,并返回相关的搜索结果。全文检索广泛应用于各种信息管理系统和应用中,如搜索引擎、文档管理系统、电子邮件客户端、新闻…...
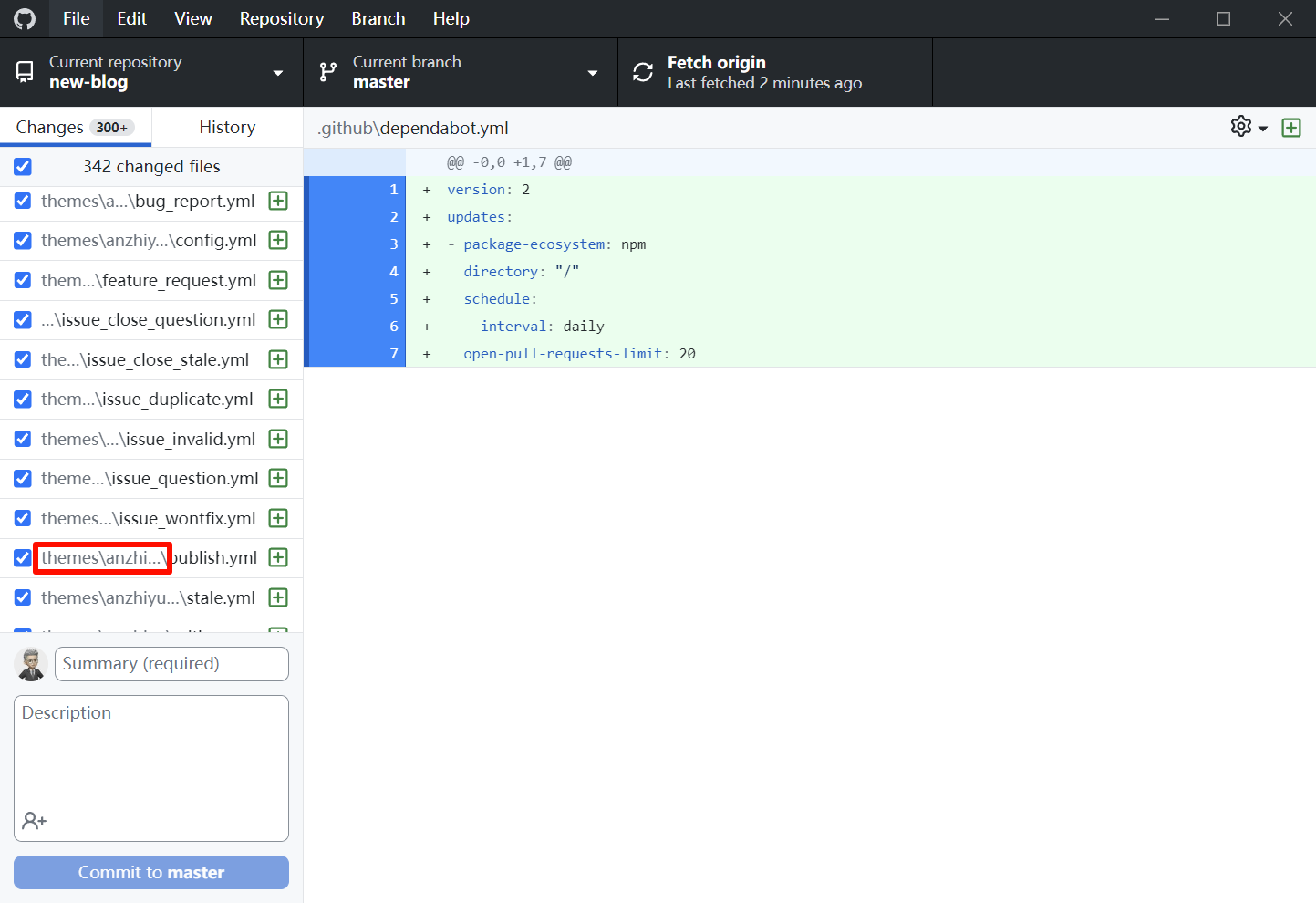
Github上传时报错The file path is empty的解决办法
问题截图 文件夹明明不是空的,却怎么都上传不上去。 解决方案: 打开隐藏文件的开关,删除原作者的.git文件 如图所示: 上传成功!...
Adobe Bridge BR v14.0.3 安装教程 (多媒体文件组织管理工具)
Adobe系列软件安装目录 一、Adobe Photoshop PS 25.6.0 安装教程 (最流行的图像设计软件) 二、Adobe Media Encoder ME v24.3.0 安装教程 (视频和音频编码渲染工具) 三、Adobe Premiere Pro v24.3.0 安装教程 (领先的视频编辑软件) 四、Adobe After Effects AE v24.3.0 安装…...

嵌入式学习——3——TCP-UDP 数据交互,握手,挥手
1、更新源 cd /etc/apt/ sudo cp sources.list sources.list.save 将原镜像备份 sudo vim sources.list 将原镜像修改成阿里源/清华源,如所述 阿里源 deb http://mirrors.aliyun.com/ubuntu/ bionic main …...

【LeetCode】【3】无重复字符的最长子串(1113字)
文章目录 [toc]题目描述样例输入输出与解释样例1样例2样例3 提示Python实现滑动窗口 个人主页:丷从心 系列专栏:LeetCode 刷题指南:LeetCode刷题指南 题目描述 给定一个字符串s,请你找出其中不含有重复字符的最长子串的长度 样…...

溪谷联运SDK功能全面解析
近期,备受用户关注的手游联运10.0.0版本上线了,不少用户也选择了版本更新,其中也再次迎来了SDK的更新。溪谷软件和大家一起盘点一下溪谷SDK的功能都有哪些吧。 一、溪谷SDK具有完整的运营功能和高度扩展性 1.登录:登录是SDK最基础…...

Vitis HLS 学习笔记--控制驱动TLP - Dataflow视图
目录 1. 简介 2. 功能特性 2.1 Dataflow Viewer 的功能 2.2 Dataflow 和 Pipeline 的区别 3. 具体演示 4. 总结 1. 简介 Dataflow视图,即数据流查看器。 DATAFLOW优化属于一种动态优化过程,其完整性依赖于与RTL协同仿真的完成。因此,…...

蓝桥杯物联网竞赛_STM32L071KBU6_关于sizo of函数产生的BUG
首先现象是我在用LORA发送信息的时候,左边显示长度是8而右边接收到的数据长度却是4 我以为是OLED显示屏坏了,又或者是我想搞创新用了const char* 类型强制转换数据的原因,结果发现都不是 void Function_SendMsg( unsigned char* data){unsi…...
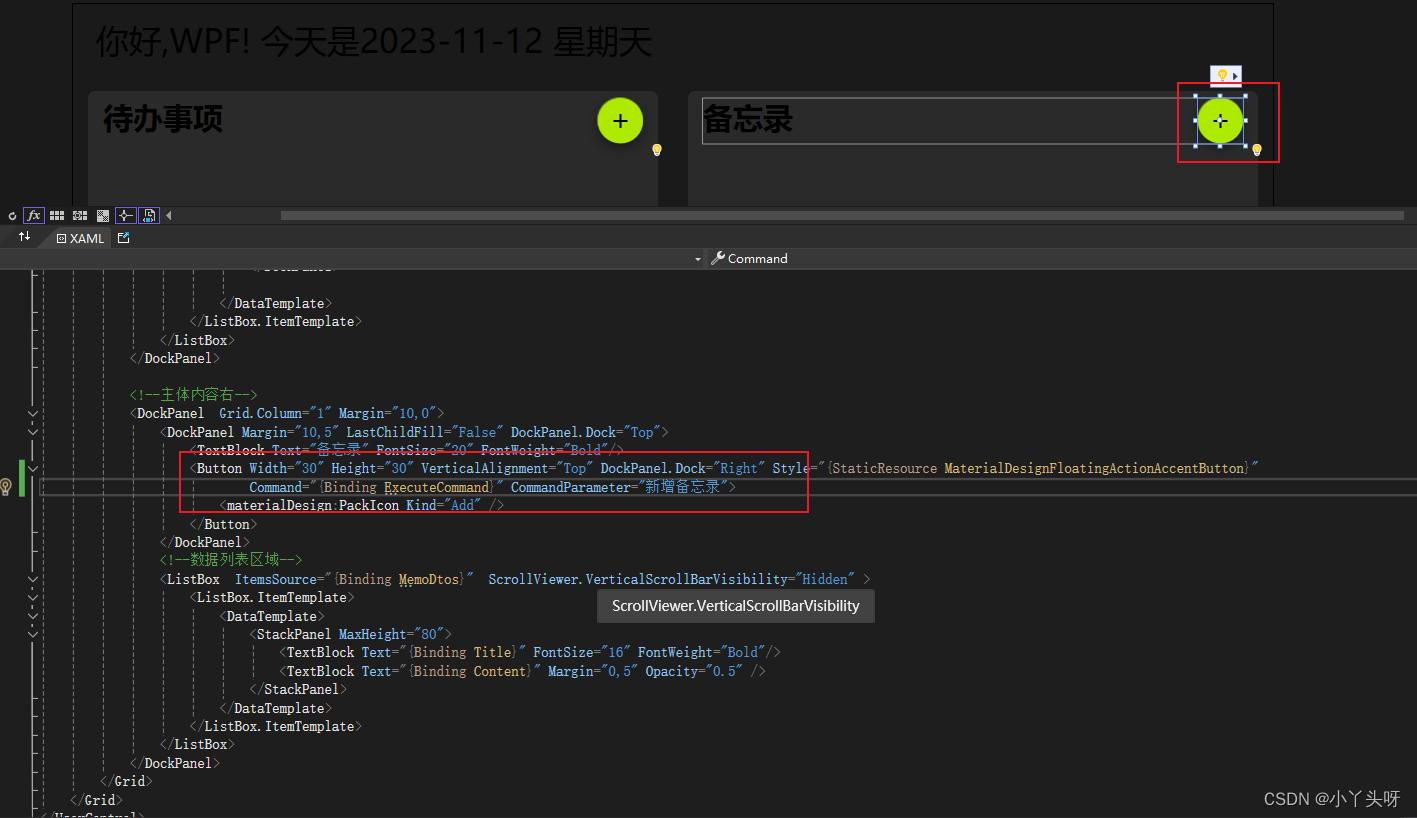
Wpf 使用 Prism 实战开发Day22
客户端添加IDialogService 弹窗服务 在首页点击添加备忘录或待办事项按钮的时候,希望有一个弹窗,进行相对应的内容添加操作。 一.在Views文件夹中,再创建一个Dialog 文件夹,用于放置备忘录和待办事项的弹窗界面。 1.1 备忘录&…...

遍历列表
自学python如何成为大佬(目录):https://blog.csdn.net/weixin_67859959/article/details/139049996?spm1001.2014.3001.5501 遍历列表中的所有元素是常用的一种操作,在遍历的过程中可以完成查询、处理等功能。在生活中,如果想要去商场买一件衣服&#…...
创建vue工程、Vue项目的目录结构、Vue项目-启动、API风格
环境准备 介绍:create-vue是Vue官方提供的最新的脚手架工具,用于快速生成一个工程化的Vue项目create-vue提供如下功能: 统一的目录结构 本地调试 热部署 单元测试 集成打包依赖环境:NodeJS 安装NodeJS 一、 创建vue工程 npm 类…...

为了更全面地分析开发人员容易被骗的原因和提供更加深入的防范措施
为了更全面地分析开发人员容易被骗的原因和提供更加深入的防范措施,我们可以进一步探讨以下几个方面: 深入技术细节 不安全的代码注释和文档: 原因:开发人员在代码注释中可能会无意间透露敏感信息,如API密钥、密码或系…...
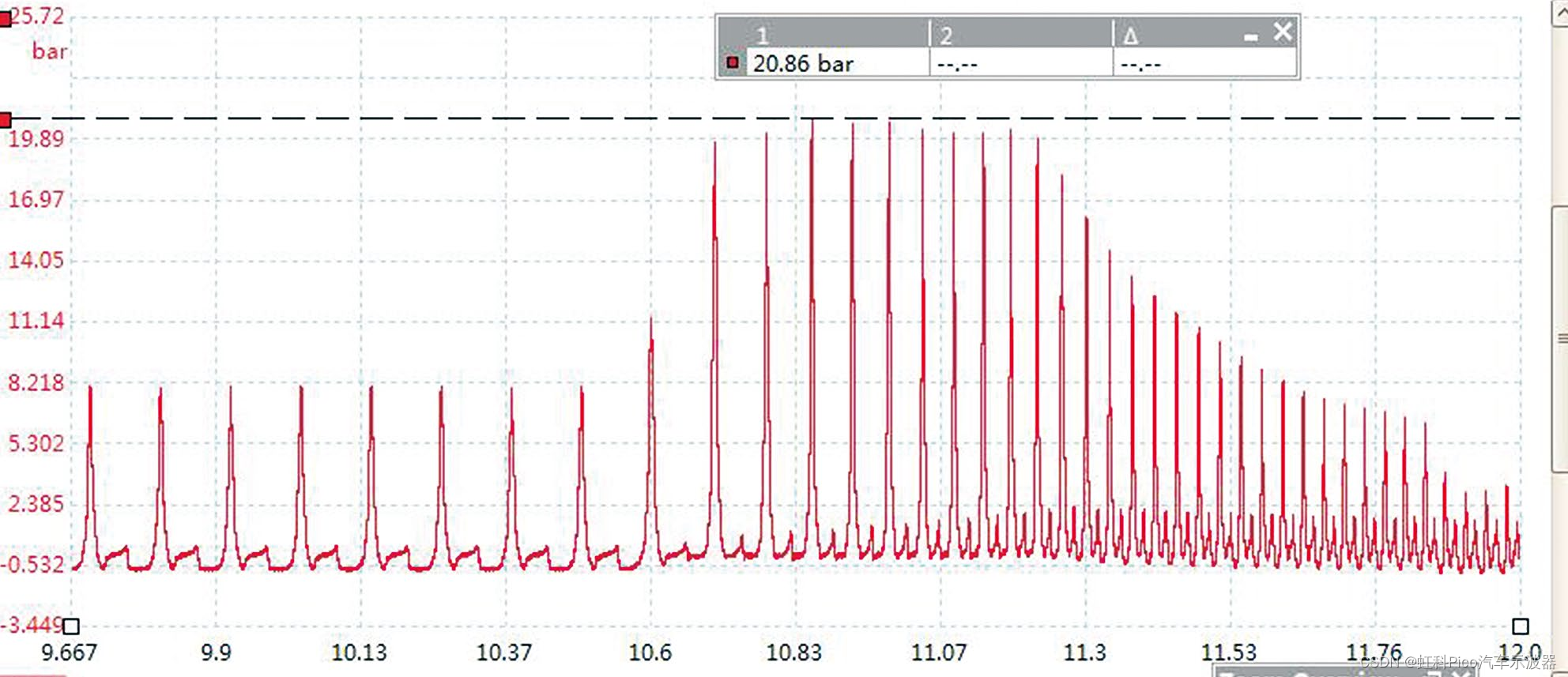
虹科Pico汽车示波器 | 免拆诊断案例 | 2020款奔驰G350车行驶中急加速时发动机抖动
故障现象 一辆2020款奔驰G350车,搭载264 920 发动机,累计行驶里程约为2.8万km。车主反映,行驶中急加速超车时发动机抖动,同时发动机故障灯闪烁,发动机加速无力。 故障诊断 接车后反复试车发现,故障只在…...

大模型落地竞逐,云计算大厂“百舸争流”
作者 | 辰纹 来源 | 洞见新研社 从ChatGPT到Sora,从图文到视频,从通用大模型到垂直大模型……经过了1年多时间的探索,大模型进入到以落地为先的第二阶段。 行业的躁动与资本的狂热相交汇,既造就了信仰派的脚踏实地,也…...

物体检测算法-R-CNN,SSD,YOLO
物体检测算法-R-CNN,SSD,YOLO 1 R-CNN2 SSD3 Yolo总结 1 R-CNN R-CNN(Region-based Convolutional Neural Network)是一种基于区域的卷积神经网络,是第一个成功将深度学习应用到目标检测上的算法。它主要由三个步骤组…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...

uniapp 开发ios, xcode 提交app store connect 和 testflight内测
uniapp 中配置 配置manifest 文档:manifest.json 应用配置 | uni-app官网 hbuilderx中本地打包 下载IOS最新SDK 开发环境 | uni小程序SDK hbulderx 版本号:4.66 对应的sdk版本 4.66 两者必须一致 本地打包的资源导入到SDK 导入资源 | uni小程序SDK …...
详细解析)
Caliper 负载(Workload)详细解析
Caliper 负载(Workload)详细解析 负载(Workload)是 Caliper 性能测试的核心部分,它定义了测试期间要执行的具体合约调用行为和交易模式。下面我将全面深入地讲解负载的各个方面。 一、负载模块基本结构 一个典型的负载模块(如 workload.js)包含以下基本结构: use strict;/…...

uniapp 实现腾讯云IM群文件上传下载功能
UniApp 集成腾讯云IM实现群文件上传下载功能全攻略 一、功能背景与技术选型 在团队协作场景中,群文件共享是核心需求之一。本文将介绍如何基于腾讯云IMCOS,在uniapp中实现: 群内文件上传/下载文件元数据管理下载进度追踪跨平台文件预览 二…...
