三维空间坐标系变换(旋转平移)
在探究三维空间下的变换前,首先研究二位空间,因为比较直观,再推广到三维空间。
首先应该清楚的一点是:旋转、平移对于坐标系下的点以及坐标系本身而言都是相对的(运动的相对性)。
例如:
- X O Y XOY XOY坐标系不动,点 P ( x , y ) P(x, y) P(x,y)沿
顺时针方向旋转 θ \theta θ,得到点 P ′ P' P′,此时点 P ′ P' P′在 X O Y XOY XOY坐标系的坐标为 ( x ′ , y ′ ) (x', y') (x′,y′); - 点 P ( x , y ) P(x, y) P(x,y)不动,坐标轴 X O Y XOY XOY沿着
逆时针方向旋转 θ \theta θ,得到坐标轴 X ′ O Y ′ X'OY' X′OY′,此时点 P P P在 X ′ O Y ′ X'OY' X′OY′下的坐标为 ( x ′ , y ′ ) (x', y') (x′,y′)。
这两条命题是等价的。
因此,仅讨论坐标系变换。
二维空间下的坐标系变换
平移:
旋转:
注:图片来源https://www.cnblogs.com/meteoric_cry/p/7987548.html
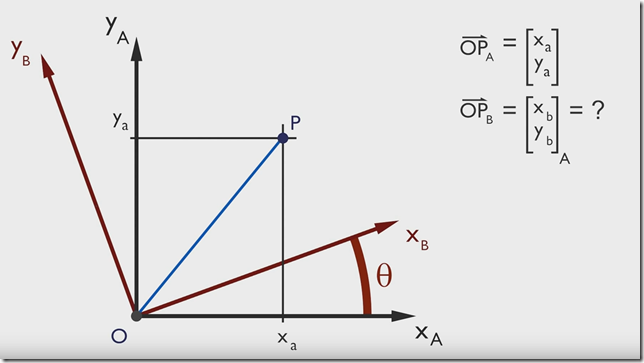
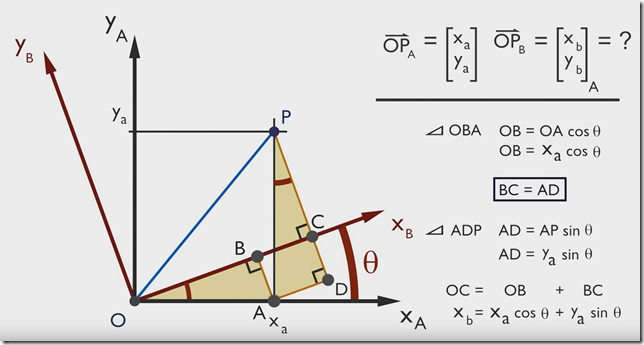
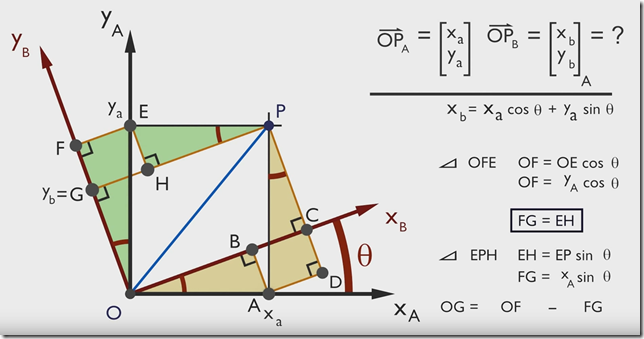
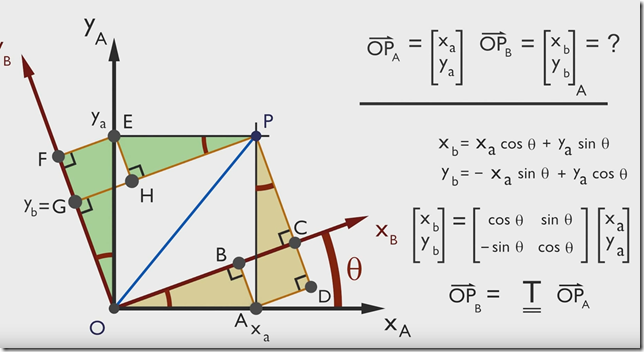
所以对于二维旋转来讲,旋转可描述为:设点 P P P在 X O Y XOY XOY坐标系下坐标为 [ x y ] \begin{bmatrix} x \\ y \end{bmatrix} [xy],将坐标系 X O Y XOY XOY顺时针旋转 θ \theta θ后, P P P点坐标为 [ x ′ y ′ ] \begin{bmatrix} x' \\ y' \end{bmatrix} [x′y′],则有:
[ x ′ y ′ ] = [ c o s θ − s i n θ s i n θ c o s θ ] [ x y ] \begin{bmatrix} x' \\ y' \end{bmatrix} =\begin{bmatrix} cos\theta & -sin\theta \\ sin\theta & cos\theta \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} [x′y′]=[cosθsinθ−sinθcosθ][xy]
旋转矩阵可记为: Q = [ c o s θ − s i n θ s i n θ c o s θ ] Q = \begin{bmatrix} cos\theta & -sin\theta \\ sin\theta & cos\theta \end{bmatrix} Q=[cosθsinθ−sinθcosθ]
三维空间下的坐标系变换
平移:
旋转:
三维空间下,当固定轴选定后,旋转就等价于:其余两轴在其平面内的(二维)旋转。
假设以逆着固定轴正向的方向看去的顺时针为旋转的正向。
-
绕 x x x轴旋转 α \alpha α(在 y z yz yz平面顺时针旋转):
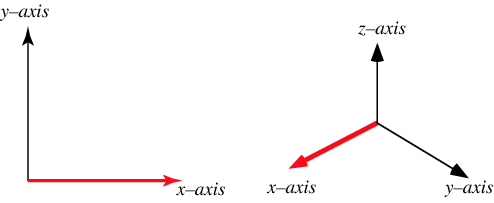
则旋转前后的坐标变化可描述为:
[ x ′ y ′ x ′ 1 ] = [ 1 0 0 0 0 c o s α − s i n α 0 0 s i n α c o s α 0 0 0 0 1 ] [ x y x 1 ] \begin{bmatrix} x' \\ y' \\ x' \\ 1 \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & cos\alpha & -sin\alpha & 0 \\ 0 & sin\alpha & cos\alpha & 0 \\ 0 &0 & 0& 1\end{bmatrix} \begin{bmatrix} x \\ y \\ x \\ 1 \end{bmatrix} x′y′x′1 = 10000cosαsinα00−sinαcosα00001 xyx1 -
绕 y y y轴旋转 β \beta β(在 x z xz xz平面顺时针旋转):
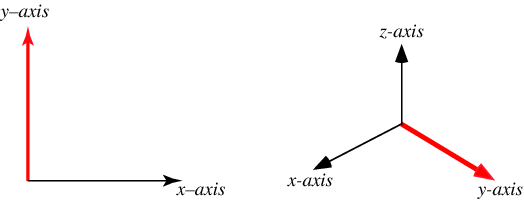
则旋转前后的坐标变化可描述为:
[ x ′ y ′ x ′ 1 ] = [ c o s β 0 s i n β 0 0 1 0 0 − s i n β 0 c o s β 0 0 0 0 1 ] [ x y x 1 ] \begin{bmatrix} x' \\ y' \\ x' \\ 1 \end{bmatrix} = \begin{bmatrix} cos\beta & 0 & sin\beta & 0 \\ 0 & 1 & 0 & 0 \\ -sin\beta & 0 & cos\beta & 0 \\ 0 &0 & 0& 1\end{bmatrix} \begin{bmatrix} x \\ y \\ x \\ 1 \end{bmatrix} x′y′x′1 = cosβ0−sinβ00100sinβ0cosβ00001 xyx1 -
绕 z z z轴旋转 γ \gamma γ(在 x y xy xy平面顺时针旋转):
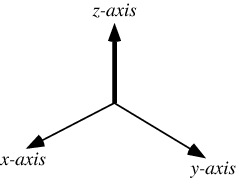
则旋转前后的坐标变化可描述为:
[ x ′ y ′ x ′ 1 ] = [ c o s γ − s i n γ 0 0 s i n γ c o s γ 0 0 0 0 1 0 0 0 0 1 ] [ x y x 1 ] \begin{bmatrix} x' \\ y' \\ x' \\ 1 \end{bmatrix} = \begin{bmatrix} cos\gamma & -sin\gamma & 0 & 0 \\ sin\gamma & cos\gamma & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 &0 & 0& 1\end{bmatrix} \begin{bmatrix} x \\ y \\ x \\ 1 \end{bmatrix} x′y′x′1 = cosγsinγ00−sinγcosγ0000100001 xyx1
综上,当坐标系沿着 X , Y , Z X,Y,Z X,Y,Z轴分别旋转 α , β , γ \alpha,\beta,\gamma α,β,γ后,旋转矩阵为3个沿单一坐标轴旋转的旋转矩阵的乘积,前后的坐标变化可描述为:
Reference:
- 旋转矩阵(Rotation Matrix)的推导及其应用
- Wolfram MathWorld: Rotation Matrix
- 3d变换基础:平移、旋转、缩放(仿射变换)详解——公式推导
相关文章:

三维空间坐标系变换(旋转平移)
在探究三维空间下的变换前,首先研究二位空间,因为比较直观,再推广到三维空间。 首先应该清楚的一点是:旋转、平移对于坐标系下的点以及坐标系本身而言都是相对的(运动的相对性)。 例如: X O Y …...

OC笔记之foundation框架
OC学习笔记(三) 文章目录 OC学习笔记(三)常用Foundation框架结构体NSRangeNSRange结构体的定义定义 NSRange 的方法打印Range的相关信息NSRange的实际运用查找子字符串返回NSRange结构体 NSPointNSRect NSStringNSString的创建NSS…...
Docker部署springboot包并联通MySQL
Docker部署jar 实现功能 部署springboot下发布的jar包不同docker容器之间通信(如MySQL访问、Redis访问)多个jar包部署 参考文献 Just a moment… Just a moment… https://www.jb51.net/article/279449.htm springboot配置 这里使用多yaml配置文件&…...

多帧激光点云基于标定参数进行融合拼接
1、前言 在三维视觉技术蓬勃发展的今天,点云作为捕获和表示三维环境的基础数据形式,扮演着至关重要的角色。点云融合拼接技术,作为连接孤立点云片段、构建连续、全面三维场景的核心过程,对于自动驾驶、机器人导航、三维建模以及地…...

python数据类型之字符串
目录 1.字符串概念和注意事项 2.字符串内置函数 3.字符串的索引、切片和遍历 4.字符串运算符 5.字符串常用方法 性质判断 开头结尾判断 是否存在某个子串 大小写等格式转化 子串替换 删除两端空白字符 格式化字符串 分割与合并 6.字符串模板 7.exec 函数 8.字符…...

Vue3实战笔记(38)—粒子特效终章
文章目录 前言一、怎样使用官方提供的特效二、海葵特效总结 前言 官方还有很多漂亮的特效,但是vue3只有一个demo,例如我前面实现的两个页面就耗费了一些时间,今天记录一下tsparticles官方内置的几个特效的使用方法,一般这几个就足…...
晶体振荡器
一、晶振与晶体区别 晶振是有源晶振的简称,又叫振荡器,英文名称是oscillator,内部有时钟电路,只需供电便可产生振荡信号;晶体是无源晶振的简称,也叫谐振器,英文名称是crystal,是无极…...

单词可交互的弧形文本
在一个项目中,要求把少儿读本做成电子教材呈现出来,电子书的排版要求跟纸质书一致。其中,英语书有个需求:书中有些不规则排版的文本(如下图所示),当随书音频播放时,被读到的文本要求…...
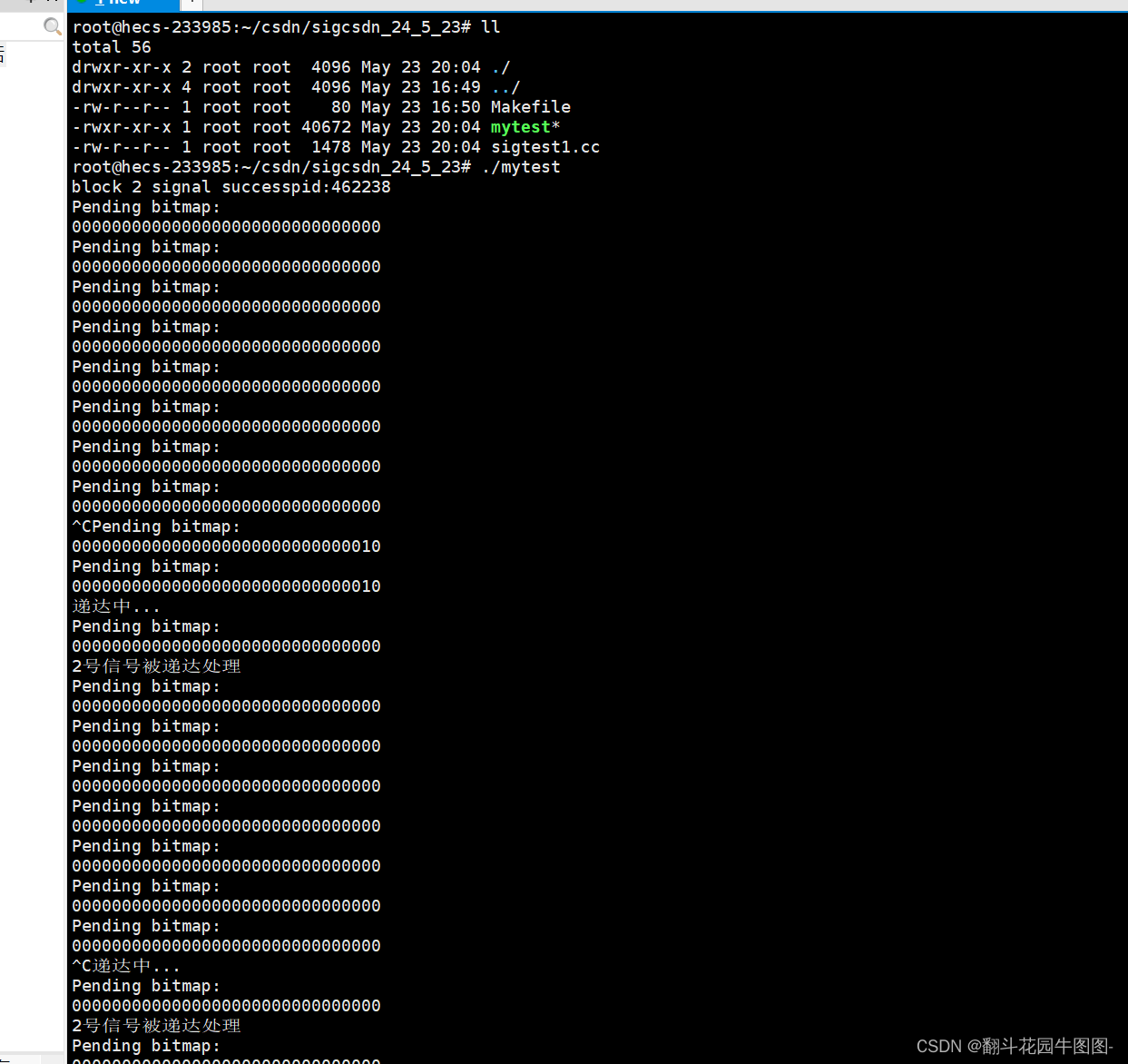
Linux——进程信号(一)
1.信号入门 1.1生活中的信号 什么是信号? 结合实际红绿灯、闹钟、游戏中的"!"等等这些都是信号。 以红绿灯为例子: 一看到红绿灯我们就知道:红灯停、绿灯行;我们不仅知道它是一个红绿灯而且知道当其出现不同的状况…...
)
centos9 stream在线安装NVIDIA驱动(rockylinux9.4也成功安装nvidia驱动)
Install NVIDIA Drivers on CentOS Stream 9(rockylinux9.4成功) 主板为技嘉mz72-hb2 显卡为4090 一.Disable Secure Boot From the BIOS 二.Enabling the EPEL Repository on CentOS Stream 9 1.update the DNF package repository cache sudo dnf …...

springmvc不同格式的参数解析
参数解析 application/x-www-form-urlencoded格式 这种格式就是传统的表单提交格式,就是一个个的键值对,会进行url编码,使用springmvc接收时使用RequestParam来进行接收,与传入的字段一一对应,此时使用的参数处理器是R…...

Unity3D让BoxCollider根据子物体生成自适应大小
系列文章目录 unity工具 文章目录 系列文章目录unity工具 👉前言👉一、编辑器添加👉二、代码动态添加的方法(第一种)👉三、代码动态添加的方法(第二种)👉四、重新设置模型的中心点👉壁纸分享👉…...
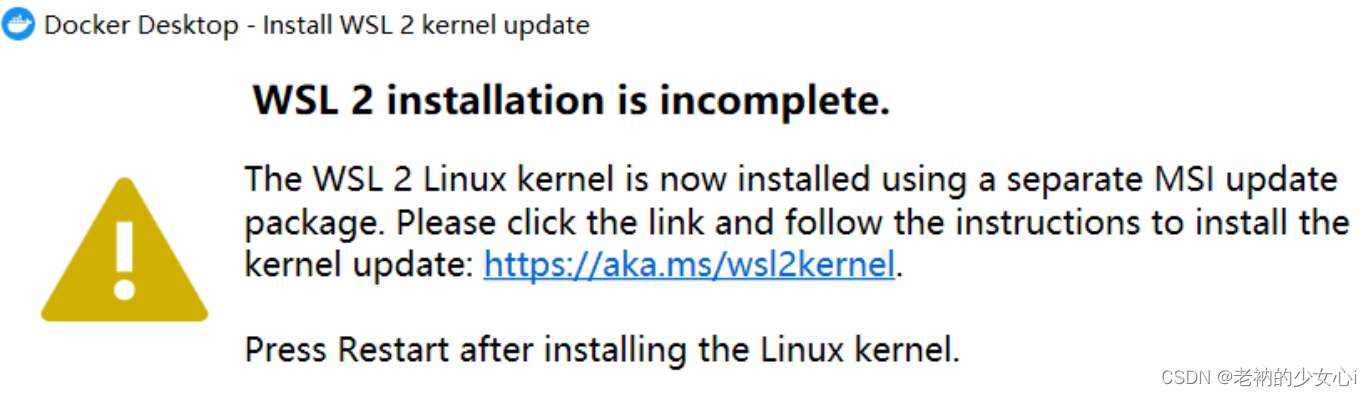
WSL 2 installation is incomplete.
使用的wsl2版本很旧,因此需要手动更新。 https://wslstorestorage.blob.core.windows.net/wslblob/wsl_update_x64.msi...
Servlet的request对象
request对象的继承关系 1.HttpServletRequest接口继承了ServletRequest接口,对其父接口进行了扩展,可以处理满足所有http协议的请求 2.HttpServletRequest和ServletRequest都是接口,不能创建对象,因此在tomcat底层定义实现类并创…...

蓝桥杯-合并数列
小明发现有很多方案可以把一个很大的正整数拆成若干正整数的和。他采取了其中两种方案,分别将它们列为两个数组 {a1, a2, …, an} 和 {b1, b2, …, bm}。两个数组的和相同。 定义一次合并操作可以将某数组内相邻的两个数合并为一个新数,新数的值是原来两…...

《web应用技术》第9次课后作业
一、将前面的代码继续完善功能 1、采用XML映射文件的形式来映射sql语句; 2、采用动态sql语句的方式,实现条件查询的分页。 二、学习git的使用。 1、每个小组将自己的项目上传到gitee,学会协作开发; 2、学会从gitee上拉取项目…...
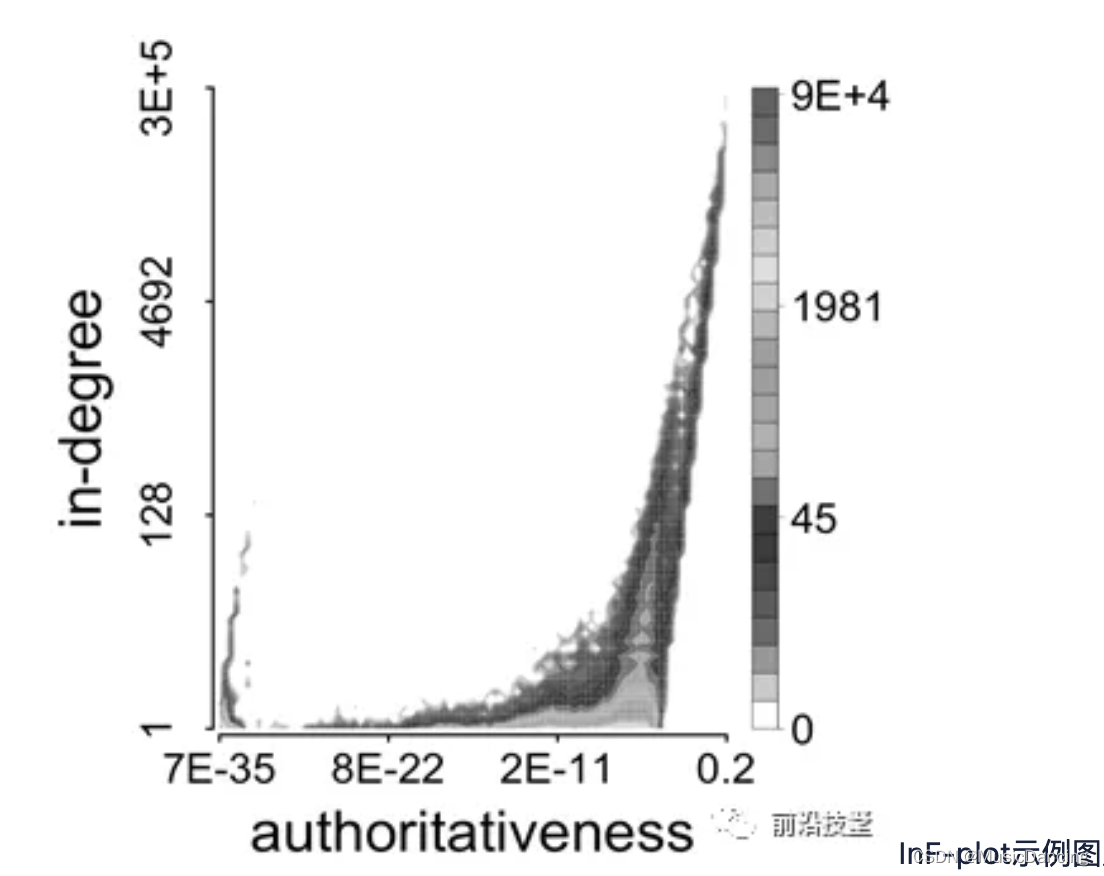
FRAUDARCatchSync算法简介
参考:https://blog.51cto.com/u_15127663/2778705 1. 背景 Fraudar 要解决的问题是:找出社交网络中最善于伪装的虚假用户簇。虚假用户会通过增加和正常用户的联系来进行伪装,而这些伪装(边)会形成一个很密集的子网络,可以通过定义…...
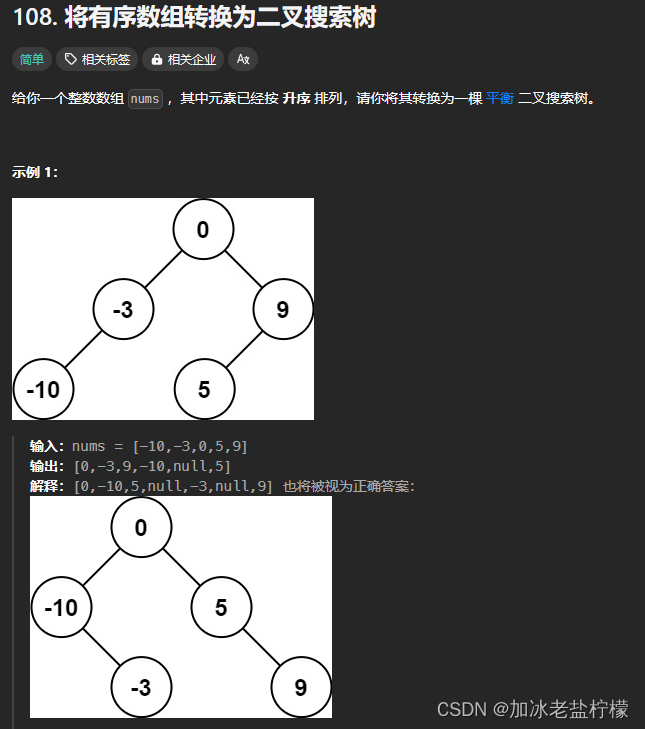
刷题之将有序数组转换成二叉搜索树(leetcode)
将有序数组转换成二叉搜索树 正常递归,中序遍历 递归经常会把自己绕晕,还是得画图分析 /*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(null…...
)
K-means聚类模型教程(个人总结版)
K-means聚类是一种广泛应用于数据挖掘和数据分析的无监督学习算法。它通过将数据点分成K个簇(cluster),使得同一簇内的数据点之间的相似度最大,不同簇之间的相似度最小。本文将详细介绍K-means聚类算法的背景、基本原理、具体实现…...

android怎么告诉系统不要回收
在Android中,如果你想告诉系统不要回收你的应用程序,可以通过设置Activity的属性来实现。你可以设置android:configChanges属性,指定在哪些配置更改时不重新创建Activity。 例如,如果你想指示系统在屏幕方向更改时不要重新创建Ac…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...

比较数据迁移后MySQL数据库和OceanBase数据仓库中的表
设计一个MySQL数据库和OceanBase数据仓库的表数据比较的详细程序流程,两张表是相同的结构,都有整型主键id字段,需要每次从数据库分批取得2000条数据,用于比较,比较操作的同时可以再取2000条数据,等上一次比较完成之后,开始比较,直到比较完所有的数据。比较操作需要比较…...
